Methodological principles of space vehicle design for the maximum energy supply of the payload
Автор: Chebotarev V.E., Fatkulin R.F., Vorontsova E.O., Shangina E.A., Balandina T.N.
Журнал: Siberian Aerospace Journal @vestnik-sibsau-en
Рубрика: Aviation and spacecraft engineering
Статья в выпуске: 1 vol.23, 2022 года.
Бесплатный доступ
The design of spacecraft at the initial stages is carried out in the presence of uncertainties in terms of parameters and conditions. The determination of design parameters is performed step by step: determination of the nominal values of design parameters, normalization of resource reserves (mass, volume, energy consumption) according to the design parameters to parry uncertainties, designing spacecraft for marginal resources. The operation of spacecraft with an electrical load switched on includes several stages: launching into the target orbit, putting into regular operation, regular operation for the intended purpose, decommissioning from the intended use in case of emergencies. The power supply system is designed to provide uninterrupted autonomous power supply to the onboard equipment in all modes and at all stages during the period of active existence of spacecraft, taking into account the presence of shadow zones of the orbit from the Earth and the Moon. In this article, the methodological principles for designing spacecraft for the maximum power supply of payload in the presence of uncertainties in parameters and conditions are developed. The mathematical models for calculating the parameters of the energy balance of spacecraft have been developed for various options for realizing the power of the session load, depending on the level of illumination of the orbit and the period of operation of spacecraft. The effectiveness of using the methodological principles of designing spacecraft for the maximum power supply of the payload, depending on the level of illumination of the orbit and the period of operation of spacecraft, has been evaluated. A technique has been developed for rationing reserves by spacecraft energy resources to parry uncertainties in terms of parameters and conditions, as well as the principles of its application when designing spacecraft for maximum payload power supply.
Spacecraft, payload, energy balance, shadow zones of the orbit, methodology for evaluating efficiency
Короткий адрес: https://sciup.org/148329613
IDR: 148329613 | УДК: 629.783 | DOI: 10.31772/2712-8970-2022-23-1-116-127
Текст научной статьи Methodological principles of space vehicle design for the maximum energy supply of the payload
The design of spacecraft at the initial stages is carried out in the presence of uncertainties in terms of parameters and conditions. Therefore, the determination of the design parameters of spacecraft under conditions of uncertainty belongs to the class of stochastic problems, and to simplify its solution and partially reduce it to a deterministic form, it is carried out step by step [1; 3–6]:
-
– determination of nominal values of design parameters;
– normalization of resource reserves (mass, volume, energy consumption) according to the design parameters to parry uncertainties;
– designing spacecraft for limiting resources.
The article considers the methodological principles of designing spacecraft for the maximum power supply of the payload when solving the problem of forming requirements for the power supply system under conditions of uncertainty.
Generalized characteristics of the electrical load of spacecraft
Information support spacecraft belong to the class of automatic spacecraft with an autonomous principle of operation over long time intervals during its active lifetime in orbit [1].
The operation of the spacecraft with the electrical load switched on includes several stages: launching into the target orbit, putting into normal operation, normal operation for the intended purpose, and decommissioning from the intended use in case of emergencies. The power supply system (PSS) is designed to provide uninterrupted autonomous power supply to the onboard equipment in all modes and at all stages during the active existence of the spacecraft, taking into account the presence of shadow orbital zones from the Earth and the Moon [1; 2].
The operating modes of spacecraft by stages differ in the distribution of the electrical load over time: at the initial stages, the modes have a variable duration and an individual energy consumption cyclogram, while at the stage of normal operation, the operating modes of spacecraft are characterized by a certain cyclicity, multiple of the spacecraft circulation period ( TSC ) or a day . In general, the spacecraft power consumption sequence diagram for each mode is presented as a piecewise continuous function - a sequence of variable load power values at the intervals of a given duration within the selected cycle.
For the design estimates of the energy balance of spacecraft, as a rule, the generalized properties of the cyclogram of energy consumption of the spacecraft of a single orbit with the duration T SC are used: the average load power per turn Pal , the average power of standby load per turn Psl , the average session load power Pssh in the shadow zone of the orbit with the duration t Sh the average session load power P si in the illuminated zone of the orbit with the duration T SC - t Sh [1]:
Р^^Ч1-^-^
Orbital illumination conditions during the year change significantly depending on the position of the Sun relative to the spacecraft orbital plane (angle η s ): from the maximally illuminated orbit, in which there are no shadow zones, to the maximally shadow orbit, when the spacecraft crosses the maximum angular dimensions of the shadow from the Earth.
The condition for the appearance of a cycle of shadow orbits during half a year has the form [1; 7; 9–11]
o
where r SC – current value of the orbit radius; RE – middle radius of the Earth ( RE = 6371 km); PsH
– angular radius of the shadow from the Earth.
The law of change in the position of the Sun relative to the plane of the spacecraft orbit during half a year for the limiting case (the ascending node of the scacecraft orbit is located at the spring point is determined by the following equation sinjjs = sinus/ sin(i — s) (3)
where i – orbital inclination; ε – ecliptic inclination; ε = 23,45; uс – the angular position of the Sun relative to the spring point.
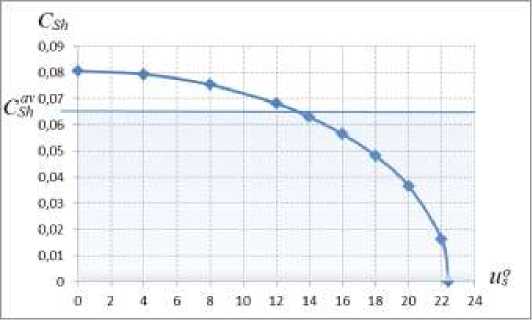
The duration of the cycle of shadow orbits is determined using the equation (3) from the condition 0 For circular orbits, the calculation of the relative duration of shadow zones from the Earth is carried out using the following equation CSH= ^^ = “ arccos ^^^S—^, , 0s< uspr, (5) where TSC – duration of a revolution; tShZE – duration of shadow zones from the Earth The maximum value of CSh at ηs = 0 equals For example, for GLONASS circular orbits we have [1; 8] SH = 14.5 degrees, ^ShZE = 0.0806, i = 64,5 degrees, us = 22.4 degrees. The dependence of CSh on us is shown in Fig. 1, and its average value in the zone of shadow orbits 0s< uspris C^J = 0.0636. In this case, the average value CSh for the cycle of shadow and solar orbits is determined from the equationC& = CsL 2 -^= 0,0636-^= 0.0158. Рис. 1. Зависимость K от угла u в зоне теневых орбит fig. 1. dependence of CSh on the angle u in the zone of shadow orbits Design estimates of the spacecraft energy balance The energy capabilities of the PSS using solar batteries (SB) as a generator are calculated from the condition of meeting the needs of the electrical load of the spacecraft in a critical case: in normal mode, at the end of the life of the spacecraft and in shadow orbits, with the check to ensure positive energy balance in each separate mode at any stage [1; 2]. The criterion for a positive energy balance is the presence of electricity supply in the electric battery (EB) at any moment of the operating mode, provided that at the beginning and end of the cycle the battery is fully charged Wmin < WE3 < Wd£B To determine the design requirements for the power of the SB and the energy intensity of the EB, the energy balance of the spacecraft is estimated under the following assumptions: – the duration of the cycle is equal to the duration of the revolution TSC; – relative duration of shadow orbital zones from the Earth according to the formula (5); – the possibility of passing shadow orbital zones from the Moon with the relative duration of more than CShZE is assessed separately as an extreme event, similar to emergency situations; – SB power in the illuminated part of the orbit is constant and equal to its average value PSB av; – the cyclogram of the normal mode is used (1), the load power is presented in the form of the components: duty PS.L, constant along the revolution, session (over duty) Ps.i and Ps.sh. Let us consider the basic option, when the session load works continuously along the revolution, including the shadow zones from the Earth, with some difference in power. For the basic logic of the operation, we calculate the energy balance of the spacecraft in the normal mode according to the method [1] and determine the requirements for the nominal value of the power of the SB at the end of the active lifetime of the spacecraft in the presence of shadow orbital segments from the Earth: – energy balance (1 - Csh) ■ рЕВ ■ Pch£B = P^B -Csh<^ (8) – SB power W /1+№л.л J A -- CS*--- – EB energy volume Ывв.п™ = Wm[n + W^b, W^b = 7^ ' Csh ■ Tsc where Wmin – the minimum value of the energy reserve in EB; Wd.EB – discharge energy capacity of the EB in the process of implementing this mode of the spacecraft; PSB.Sh – SB power at the end of the life of the spacecraft in shadow orbits; P ch-EB – EB charge power; Pd.EB – EB discharge power; ^n , ^SB , ^ch-w –Power Conversion Efficiency in Power Supply Systems; ^ CB – Efficiency of energy conversion in EB. PSB.i=^--(l+Ash-)(11) Therefore, in the solar orbit CSh = 0, ASh = 0 there is an excess of the generated power of the SB SPSBSh = S'(1 + Ash)’ PSB0 =(12) Due to the degradation of the SB power during the active lifetime (tAL), its initial nominal value Pss must be increased where αd – SB degradation factor. The excess of the generated power of the SB at the beginning of the active lifetime will be pSBSh For example, for the GLONASS circular orbits we have The analysis of the above equations shows that in the initial periods of the spacecraft operation, as well as in solar orbits, reserves of energy resources are always formed due to the degradation of the SB power by the end of the active lifetime and the variable duration of the shadow zones from the Earth in the spacecraft orbit [1]. The developed design model for calculating the energy balance makes it possible to formulate the requirements for the initial power of the SB psb (formulae (9), (13)) and for the nominal discharge energy WEB.nom (formula (10)) for the known load parameters and orbit illumination conditions. At the same time, the energy intensity of the EB is set for the case of the maximum shadow zones from the Earth and at the beginning of the active lifetime, with the maximum power consumption of the session load in the shadow zones from the Earth. Efficiency of application of adaptive session load The adaptive session load is implemented by regulating the power of its consumption during the active lifetime, based on the available energy capabilities of the SB in shadow and solar orbits, at the beginning and at the end of the operation period. The range of change in the power consumption of the session load is determined by the formulae (12), (13) for the case of the solar orbit at the beginning of the active lifetime (the maximum value max , - . . , . . pminA ^ci ) and at the end of the active lifetime (the minimum value ) pmin _ Чспл^^^^^ S i+^Sh The current value of the power consumption of the session load Ps is determined by the formulae (12)–(15): p _nch^n^k^l)^ = Psi+P?in Г s ^Sh Sl ^Sh FV si The average value of the power consumption of the session load is determined by integrating the equation (16) under the assumption that the average value of Aav is constant: The effectiveness of adaptive session load is proposed to be evaluated using the relative criterion = ^(Н^д;)-(ШМ)-^ sa P™ exP(-a3tM)-(l+5P,I)-(l+4Jk)«Psi When applying the adaptive session load, the energy intensity of the EB is set for the case of the maximum shadow zones from the Earth and at the beginning of the active lifetime at the maximum power consumption of the session load p .„max 'in For example, for the GLONASS circular orbits we have [1; 8]: ASh ≈ 0.11, at CSk = 0.0158 we obtain Aav ≈ 0.0138, at αd ∙ tAl = 0.2 we obtain I0 ≈ 0.9063, as a result, assuming that „max ^ O.S we obtain δPea ≈ 1.4. The obtained estimates confirm the efficiency of using the adaptive session load. Efficiency of reducing the session load power in the shadow zones of the orbit Let us consider the option of optimizing the power supply of the spacecraft by reducing the power of the session load in the shadow zones of the orbit ^s^h — ar‘ ^s> ^si — ^s.2 (20) where αr – session load power reduction factor in the shadow orbital zones from the Earth. For this option, the SB power at the end of the active lifetime is determined by the formula (9): ^SB.2 Psl+Ps.2 VsB • Pn ?SB.2 — ^SB ' exP( ad ' ^AL^ Assuming the same SB power at the end of the active lifetime of ^SB.l ?SB.2 , we estimate the increase in the power of the spacecraft session load in this option 8p _ ^2 _ 11 As ft 3 P, l+^Ask The maximum value of δPs is achieved at αr = 0. ^ = 1+^ The obtained value of the session load power gain is realized in shadow orbits at the end of the active lifetime (tAL) when the maximum degradation of the SB power occurs. However, the presence of excess SB power in the initial period, when the life of the spacecraft tf is less than tAL allows us to ensure the work of session load with the increased power Ps.2 in shadow orbital zones from the Earth up to a certain time of operation (0 ≤ tf ≤ tAL). Р$ВЗ — ^SB ' exp( ad ■ f/) — ’ (1 + ^Sh) The value of ^ SB is determined from the equation (13), which is substituted into the equation (24) PSB.3 _ PSB2 exp(-a9tf) exp{-a9tA]}’ (tjl-£/).«. = ln^ The equation (25) can be converted to the following form -^ = 1---— In—, SPsl2 = ^ *AL «а*А1 l+ar-Xsft+(l+^SA)-3Pi[2' !U Ps2 Using the equation (26), we form the generalized shadow coefficient for the cycle ^=(‘-3c" Thus, we can conclude that reducing the power of the session load in the shadow zones of the orbit only at the final stages of the active lifetime ( tf ≤ tAL) allows increasing the power of the session load (δPS2), which is equivalent to an increase in the target efficiency. However, in this case, the availability factor of the spacecraft at the system point decreases due to the increase in the time taken to remove the spacecraft from its intended use during the cycle. To evaluate the efficiency of payload shutdown in shadow orbital zones from the Earth, we use the relative criterion δPET the product of the increase in the efficiency and readiness of the spacecraft ^fr = ^-(с;-дс)> i (28) where ^A – normalized value of the spacecraft availability factor at the system point; ΔC – change in the spacecraft readiness factor. As an indicator ΔC, it is possible to use one of the indicators of shadow orbital zones from the Earth: Г CAL, ^Sh , Lsh. Substituting into the equation (28) the value δPs from the equation (22) we obtain the limit on the power reduction factor (αr): 0 < < a_ aД Ash' 1 In the option of switching off the session load in the shadow orbital zones from the Earth at the end of the active lifetime, the energy intensity of the EB is set for the case of the maximum shadow orbital zones from the Earth and at the beginning of the active lifetime, with the maximum power consumption of the session load in the shadow orbital zones from the Earth (19). For example, for the GLONASS circular orbits we have [1; 8]: _4Sh ^ 0.11 at — °-2 and SPr2 * 0.5 we obtain ~ = 068 and, respectively, ^ГЪ= (1- 0.68)∙0.0158 = 0.005. Assuming that ^a = 0.995, we obtain a set of restrictions on αr depending on the values ΔC (Table 1). Dependences of performance factors on ΔK ΔC CShZE = 0.08 ^Sh = 0.0636 Cs* = 0.0158 csh = 0.005 αr.pr (at δPET >1) 0.14 0.308 0.79 0.899 δPET (at αr.pr = 0) 1.016 1.034 1.087 1.1 Reserves rationing method for spacecraft energy resources The design of spacecraft power supply systems at the initial stages is carried out in the presence of uncertainties in terms of the regular spacecraft operation program, electrical load parameters, and lighting conditions. Therefore, the design parameters of the spacecraft power supply system (SB power, EB power consumption) are determined when calculating the energy balance for the worst conditions: at the end of the spacecraft active life and at the maximum duration of the shadow orbital zones from the Earth. The presence of uncertainties in the implementation of the energy parameters of the spacecraft leads to the need to normalize the energy reserves in terms of power of the electrical load, SB power and EB energy intensity. The power of the electrical load of spacecraft in various modes is formed as the sum of the powers of the electrical load of spacecraft components, for each of which restrictions are set in the form of a range P - ∆P ≤ P ≤ P + ΔP, δP = i , Pi where P, Pi –actual and nominal values of energy consumption of the i-х components of the spacecraft; ΔPi –limit range of deviation of energy consumption from the nominal value of the i-х components, set by the method of expert assessments, within the limits δPi = 0,05–0,15, depending on the novelty of the developed equipment. The energy consumption of spacecraft as the sum of random values of its constituent parts with an interval distribution law, when using the principle of a guaranteed result, is formed as follows (deterministic model) [1; 5]: PSc = ^jPi However, in accordance with the central limit theorem, the sum of random variables of constituent parts with an interval law can be represented as a random variable with a normal probability distribution law (probabilistic model) [1; 3–6] ^v — tp ' aP> aP — J^i=l^^ ^ ^ ■ ?nSC where n – number of components; t – probability distribution parameter for spacecraft power con- sumption; σ – standard deviation for spacecraft power consumption; FP – probability integral (normalized Laplace function), given in a tabular form [1; 3–6]. For the level of probability at which the structural stability of the project (FP ≈ 0.997), is guaranteed, the value of the probability distribution parameter is t ≈ 2,8. Therefore, when compiling the budget of spacecraft resource reserves for parrying uncertainties, the use of a probabilistic model reduces these reserves in comparison with the deterministic model [1]: ^ = at n > 10 ЛР^ For the GLONASS spacecraft n > 25, therefore and at δPi = 0.05–0.15 we obtain AR. . ДР, =---— % 0.56 ■ 6P = 0.03 - 0.08 Spacecraft design for the maximum power supply of the payload The design of spacecraft for the maximum power supply of the payload implies the maximum use of reserves of energy resources to increase its efficiency. We have considered the option of using an adaptive session load by controlling the power consumption of the payload (controlling the duration of session work) depending on the illumination of the orbit and the life of the spacecraft. The use of an adaptive session load increases the efficiency of the spacecraft (for the spacecraft of the GLONASS system, one can obtain δPEA ≈ 1.4). In order to implement this scheme, it is necessary to develop an appropriate payload, a complex of automation and stabilization of the PSS for maximum power from the SB and the load at the initial stages of the operation of the spacecraft. When designing a thermal control system for the maximum “overheating” mode, it should be taken into account that the average heat release per revolution in this mode at the beginning and at the end of the active lifetime will be different. However, this scheme does not require reserves of energy resources to parry uncertainties. Using the session load power reduction mode in the shadow zones of the orbit makes it possible to increase the efficiency of the spacecraft (for the spacecraft of the GLONASS system, you can obtain δPET = 1,016–1,11). In this case, it is possible not to create reserves of energy resources to parry uncertainties (δPv = 0.03 - 0.08), since they can be compensated (if necessary) by reducing the power of the session load in the shadow orbital zones from the Earth. Conclusion 1. The methodological principles for designing spacecraft for the maximum power supply of the payload in the presence of uncertainties in parameters and conditions have been developed. 2. The mathematical models have been developed for calculating the parameters of the energy balance of spacecraft for various options for implementing the power of the session load, depending on the level of illumination of the orbit and the period of operation of spacecraft. 3. We have made the evaluations of the effectiveness of using the methodological principles of designing spacecraft for the maximum power supply of the payload, depending on the level of illumination of the orbit and the period of operation of the spacecraft. 4. We have developed a technique for standardizing reserves by spacecraft energy resources to parry uncertainties in terms of parameters and conditions, as well as the principles of its application when designing spacecraft for the maximum power supply of the payload.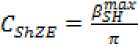
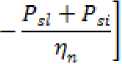
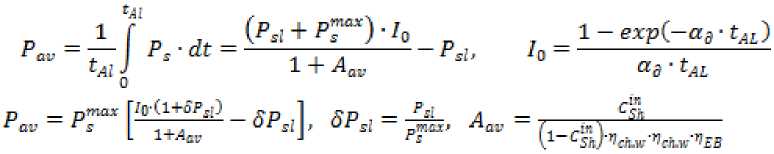
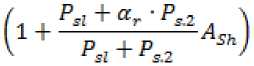
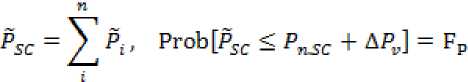
Список литературы Methodological principles of space vehicle design for the maximum energy supply of the payload
- Chebotarev V. E., Kosenko V. E. Osnovy proektirovaniya kosmicheskikh apparatov informatsionnogo obespecheniya [Fundamentals of spacecraft design information support]. Krasnoyarsk, 2011, 488 p.
- Lukyanenko M. V., Lukyanenko M. M., Lovchikov A. N., Bazilevsky A. B. Istochniki energii sistem elektrosnabzheniya kosmicheskikh apparatov [Energy sources of spacecraft power supply systems]. Krasnoyarsk, 2008, 176 p.
- Wentzel E. S. Issledovaniye operatsiy. Zadachi, printsipy, metodologiya [Operations Research. Tasks, principles, methodology]. Moscow, Nauka Publ., 1988, 208 p.
- Ilyichev A. V., Volkov V. D., Grushinsky V. A. Effektivnost’ proyektiruyemykh elementov slozhnykh system [Efficiency of designed elements of complex systems]. Moscow, Vysshaya shkola Publ., 1982, 280 p.
- Rozanov Y. A. Sluchaynyye protsessy [Random processes]. Moskow, Nauka Publ., 1979, 184 p.
- Tarakanov K. V., Ovcharov L. A, Tyryshkin A. N. Analiticheskiye metody issledovaniya system [Analytical methods for studying systems]. Moscow, Sov. Radio Publ., 1974, 240 p.
- Chernyavsky G. M. Orbity sputnikov svyazi [Orbits of communication satellites]. Moscow, Svyaz’ Publ, 1978, 240 p.
- Perova A. I., Kharisova V. N. GLONASS. Printsipy postroyeniya i funktsionirovaniya [GLONASS. Principles of construction and functioning]. Moscow, Radiotekhnika Publ., 2010, 800 p.
- Chebotarev V. E., Vorontsova E. O. [A technique for providing energy resources to a circumlunar satellite for passing shadow zones of long duration]. Kosmicheskiye apparaty i tekhnologii. 2020, No. 4, P. 233–240 (In Russ.).
- Chebotarev V. E., Vorontsova E. O., Sidorova E. A. [Modeling of Shadow Zones in Circumlunar Orbits and Peculiarities of Calculating the Parameters of Power Supply and Thermal Control Systems of a Circumlunar Spacecraft]. Reshetnevkiye chteniya. 2020. P. 49–51 (In Russ.).
- Chebotarev V. E., Vorontsova E. O. [Method for calculating the design parameters of the power supply system of a circumlunar spacecraft]. 25-ya Mezhdunarodnaya konferentsiya “Sistemnyy analiz, upravleniye i navigatsiya”, 2021, P. 150–152 (In Russ.).
- Fortexue P., Swinerd G., Stark D. Razrabotka sistem kosmicheskikh apparatov [Development of spacecraft systems]. Moscow, Al’pina Pabl., 2015, 756 p.
- Tumanov A. V., Zelentsov V. V, Shcheglov G. A. Osnovi komponovki bortovogo oborudovaniya kosmicheskih apparatov [Foundations of layout of on-Board equipment of spacecraft]. Moscow, Bauman MSTU Publ., 2010, 136 p. (In Russ.).
- Eliasberg P. E. Vvedenie v teoriyu poleta iskusstvennogo sputnika Zemli [Introduction in the theory of flight of the artificial companion of the earth]. Moscow, Librikom Publ., 2011, 544 p.
- Kosenko V. E., Zvonar V. D., Chebotarev V. E. [Lunar information and navigation support system]. Aktual’nye voprosy proektirovaniya AKA dlya fundamental’nyh i prikladnyh nauchnyh issledovanij [Actual problems of AKA design for fundamental and applied scientific research]. Khimki, FSUE S. A. Lavochkina Publ., 2015, P. 323–329 (In Russ.)


