Methods for constructing routes outside urban areas based on GPS data

Currently the idea of a healthy lifestyle is significant. People strive to monitor their health, go in for sports, and travel. They are constantly searching for different places to go. The Krasnoyarsk Krai is rich in natural resources. Krasnoyarsk obtains the “Krasnoyarsk Hiking” project, which is a network of marked paths on the territory of the Torgashinsky Ridge. Many citizens have appeared who want to go hiking both in the vicinity of their city and outside the urban area. There are many sources where people can find background information about places to go and general trails, however, there is still no way to create an individual route over rough terrain with an optimal track for an individual. Developing a system to automatically construct routes to selected places to go using GPS navigation data requires to develop an algorithm to construct the shortest route from point A to point B.

The task of constructing a tourist route is reduced to the problem of finding the shortest path from one graph vertex to another [1]. This assignments is one of the most popular in graph theory. A graph is an abstract object consisting of a set of vertexes (nodes) and a set of edges describing connections between pairs of vertexes. Routes consisting of interconnected intersections are a graph.

Methods for constructing routes are used in practice in various fields. The paper [2] considers approaches related to the development of technology for the integrated processing of remote sensing data and vector maps in order to monitor the consequences of emergency situations, identify critical areas and prevent negative consequences. The authors [3] consider the use of the discrete solution algorithm SOTA (Self-organizing Tree Algorithm) and its parallel version using CUDA in constructing a reliable shortest route using the capabilities of video cards. In [4], the authors developed a modification of the discrete algorithm for finding the route of movement in a time-dependent transport network. The authors demonstrate the effectiveness of the proposed approach on the example of a large-scale road network in Samara and achieve an effective route construction speed of less than 1 s. Also, methods for constructing routes are used for data transmission in satellite [5], organizational and economic systems [6], for monitoring the forests in satellite observation [7; 8] and in other data areas. The article discusses various methods for constructing routes and proposes an effective implementation of the Dijkstra method modification to construct tourist routes on the territory of the Torgashinsky Ridge.

Route constructing methods

Much research has been focused on the classic assignment of finding the shortest path in an open area over the years. In this regard, there is a large number of different path-search algorithms, many of which show good results in their field. Researchers [9] evaluated the efficiency of 15 shortest path search algorithms in real road networks. The authors consider the Bellman-Ford-Moore algorithms, the Dijkstra algorithm and its modifications, the Pape-Levit’s algorithm, and others. Based on the evaluation, a set of recommended algorithms to calculate the shortest paths in real road networks is determined. Also A* algorithm [10] is widely known; the algorithm is aimed at reducing the time of searching for the optimal route by excluding less promising search directions based on Dijkstra's algorithm. Modifications of the Dijkstra algorithm are used in many practical tasks, for example, finding the shortest route for tourism in Bali [11]. We propose to consider such algorithms as the Dijkstra algorithm, Levit’s algorithm and the Floyd-Warshall algorithm in more detail.

Dijkstra's algorithm is one of the most famous algorithms for finding the shortest path [12]. It allows to determine the shortest paths between vertexes. The implementation is that the algorithm "visits" one vertex at each step and tries to reduce the labels. The algorithm terminates when all vertexes have been visited. Dijkstra's algorithm has a number of advantages, such as high speed and accuracy of the result. However, the drawback is the difficulty in understanding. The computational complexity of Dijkstra's algorithm depends on how the vertex is found, the set of unvisited vertexes is stored, and the labels are updated. Therefore, we can get that the implementation in this method will require O(N) and O(1) units, respectively. Considering that the first operation is performed N times, and the second depending on the constructed graph, the complexity is O(N×N+M) , where N is the number of vertexes, and M is a constant depending on the constructed graph.

Levit's algorithm is an algorithm on graphs finding the shortest distance from one of the vertexes of the graph to all others [13]. It also works for graphs with negative edge weights. Comparing to Dijkstra method, Levit’s method fails in that some vertexes have to be processed repeatedly, but it wins in simpler algorithms for including and excluding vertexes from M1 set (M1 are vertexes, the distance to which is calculated at the current step of the algorithm). It has been established that Levit’s method is the fastest for graphs of "geometric" origin, constructed on the basis of transport networks and real distances. In addition, it wins in terms of the program size. The worst-case complexity of Levit's algorithm is O ( N ² x M ). To achieve such a running time, it is necessary the edges in the graph be arranged in lexicographic order. A more realistic estimate of this method is the average time, namely the complexity of O(N×M). However, on real graphs, Levit's algorithm is only slightly inferior to Dijkstra's algorithm.

Floyd-Warshall algorithm is used to find the shortest distances among all vertexes of a weighted graph without cycles with negative weights using the dynamic programming method [14]. The algorithm uses two adjacency matrices: the distance matrix D k and the precedence matrix S k , after which, during n iterations, where n is the number of nodes in the distance matrix, and the nth iteration, the optimal / final distance matrix D k = n is given, and also final precedence matrix S k = n.

The disadvantage of Floyd-Warshall algorithm is that the algorithm determines only the shortest distance between all pairs of vertexes, but it does not keep information about the shortest paths, which is necessary for route constructing assignments.

As a result of considering the most important algorithms for obtaining the shortest path in the graph, as well as an analysis of their advantages and disadvantages, we denote the requirements that are necessary to search for the shortest path in three-dimensional space on the territory of the Tor-gashinsky Ridge:

• –    time complexity of the algorithm;

• –    high simplicity in implementing the algorithm for a mobile application;

• –    work for graphs with positive weights;

• –    result accuracy;

• –    saving the shortest path information.

The analysis showed that searching for the shortest path in three-dimensional space on the territory of the Torgashinsky Ridge requires to use Dijkstra algorithm, since it takes into account the features of the process under consideration. The main advantages of Dijkstra's algorithm are the high speed of operation and the accuracy of the result [15].

Algorithm for constructing routes based on GPS data

Before starting a step-by-step description, we consider the algorithm operation scheme for constructing routes over rough terrain on the territory of the Torgashinsky Ridge (Fig. 1).

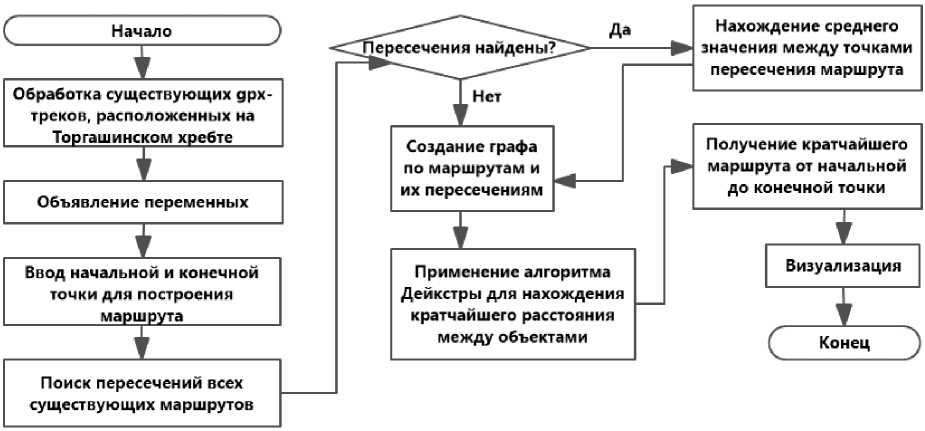
Рис. 1. Схема разработанного алгоритма построения оптимального пути

Fig. 1. Scheme of the developed algorithm for constructing various paths

The software implementation realizes twelve gpx-tracks (a free text format for storing and exchanging GPS data) of already existing routes in the Torgashinsky Ridge territory. To extract all the necessary information from these tracks, the minidom library is used, which allows to analyze the xml-markup and select the necessary information [16].

All tracks are in their tracks folder. When looping through this folder, each route is visited and the information is recorded in the corresponding fields: route name, drawing color and coordinates of each route point in the latitude, longitude and altitude format.

In the vocab dictionary, the keys in the form of the name of the route are given the corresponding gpx-tracks. Further, using this dictionary, a list of route names is formed and dictionaries are created: indices for intersection points and a graph (distances), a list of vertexes (nodes). The tuples specify the starting (st) and ending (en) points of the route to construct a new route - they consist of y and x coordinates; then they are written to the point dictionary.

When looping through vocab, the condition is checked whether the points st and en are the start or end points of existing routes, and in this case they are removed from the point list - this list allows to determine whether it is required to create new graph vertexes for Dijkstra algorithm to operate correctly.

The next step is to create a graph of routes and their intersections. To perform this operation, it is necessary to correlate each route with the others in order to determine whether there are intersections, if intersections are found, fix them. Lists are created for each route containing, respectively, x1, y1 and z1 coordinates for the first route and x2, y2 and z2 coordinates for the second route. Looping through the x1 and x2 points of the lists , the distance between the points is determined. If this distance is less than the minimum, then the minimum distance is overwritten with a new one and the indexes of the found points are saved. If the routes intersect, the arithmetic mean of the intersection point (x, y, z) is determined. This method results in finding the intersection point of the route, if the gpx-tracks do not intersect, but pass very close to each other.

To find the distance between two points, studying the shape of the Earth is required. The shape of the Earth can be described as a sphere, so the equations to calculate distances on a great circle are important to calculate the shortest distance between points on the surface of the Earth, thus, they are often used in navigation [17].

Calculating the distance by this method is more efficient and in many cases more accurate than calculating it for projected coordinates, because, firstly, for this it is not necessary to transmit geographical coordinates into a rectangular coordinate system and, secondly, many projections, if incorrectly chosen, can lead to significant length distortions due to the features of projection distortions.

A sphere with a radius of 6372795 m is used for calculations,, which can result in a smaller error than if calculated in rectangular coordinate systems.

According to the spherical cosine theorem:

δ σ = sin ^{- 1} { sin φ × sin φ + cos φ × cos φ × cos Δλ } ,                     (1)

where φ , λ , φ , λ are latitude and longitude of two points in radians; Δλ is longitude difference;

Δσ is angular difference.

To convert angular distance to metric, it is necessary to multiply the angular difference by the Earth radius, the units of the final distance will be equal to the units where meters are expressed.

The described method is implemented in the functions: Lenfor and Meters. The Lenfor function is a function to calculate the length of the path between waypoints in x and y without taking into account the height, and the Meters function is a function to calculate the distance between gps-coordinate points, taking into account the height difference, after calculating the distance by the Lenfor function.

Dijkstra algorithm determines the shortest paths between vertexes. In this implementation, the principle of this algorithm is used to determine the weights of edges, find the shortest path, and compose it from parts of gpx-tracks. Dijkstra algorithm is formulated step by step as follows:

Step 1: set the start and end of the route point.

Step 2: create a dictionary of unvisited vertexes – unvisited, a dictionary of paths to each vertex -way, a dictionary of visited vertexes - visited.

Step 3: loop while there are unvisited vertexes. Otherwise, step 10.

Step 4: if there are neighbors in unvisited positions, then new path weight (newDistance) = current path weight (currentDistance) + weight between vertexes (distance). Otherwise, step 3.

Step 5: the unvisited value is a list? If so, take the first value of the list: dist = dist[0]. Otherwise, unvisited[neighbour] = newDistance, newPath (new path part).

Step 6: write to the path dictionary newPath. Write A to visited for the current vertex, write currentDistance.

Step 7: remove a current vertex from unvisited.

Step 8: generate candidates for a new current peak. Sort newDistance in ascending order. We get the new current vertex (path) = currentDistance[1] and the current path to it (currentDistance) = cur-rentDistance[0].

Step 9: newPath = path + current(current cell).

Step 10: a completed dictionary of paths from the starting point is obtained.

Step 11: select the desired route by the endpoint key.

Step 11: determine which route the next pair of vertexes belongs to.

Step 12: if index of start point (lost) > index of end point (next), copy that part of the track. Otherwise, go to the opposite direction of the track.

Step 13: construct the optimal gps-track, according to the given points.

Experimental studies

As an example, consider one of the options to construct a route, where the starting point is Mount Tamara with coordinates 55.952562 and 92.857231, located on the route "Health", and the end point is the 2nd Torgashinsky viewpoint with coordinates 55.919239 and 92.889939, located on the route "Bolgash". Fig. 2 demonstrates a route visualization (coloured in pink).

the Torgashinsky Ridge

Рис. 2. Визуализация построенного маршрута

• Fig. 2. Visualization of the constructed route

Fig. 2 shows N.L. – northern latitude, and E.L. - Eastern longitude. We observe 13 routes in different colours, we will decipher from left to right: red – Trail "Health", purple – Trail "Ski", green – trail "Wet Log", pink – built route at the indicated points, orange – trail "Red", green – trail "Sinilga", yellow – the "Through" trail, blue – the "Sivaya" trail, purple – the "Top" trail, orange – the "Bolgash" trail, brown – the Speleologists' trail, purple – the "Kuznetsovo" trail, blue – the "Skazka" trail.

In addition to visualization, the algorithm for constructing tourist routes calculates the length of a new route, the maximum and minimum heights throughout the entire track, and the construction time. Thus, according to the constructed route, it is obtained: route length = 10676 m, maximum height = 584.53 and minimum height = 179.76. Currently, the software system has got 38 different objects of the Torgashinsky Ridge, which covers more than 95% of the points visited by tourists. At the same time, the algorithm (system) allows the input of its own coordinates, which are taken into account when constructing routes. The table shows the characteristics of some constructed routes.

Examples of the constructed routes and their characteristics

	Construction time, s	Distance, m	Height difference, m
From mountain Tamara to the 2nd Tor-gashinsky viewpoint	0,005457	10 676	404,77
From Sivye rocks up to Chernaya Sopka	0,005655	21 642	376,68
From mount. Sinilga to mount. Luch	0,004734	10 555	404,77
From non-profit partnership (NPP) "Zagorye-1" to cave Mokraya	0,005604	6 371	381,67
From rock Propast to rock Krasny Greben	0,013433	4 188	229,81
From rock Magda to NPP "Zagorye-2"	0,003422	9 849	266,07

Conclusion

As a result of the research, an algorithm is developed for constructing the shortest route from the start to the end point, based on Dijkstra algorithm, which gets the optimal gpx-track, as well as obtains a database of existing routes. The algorithm is used in a software system implemented as a website and a mobile application that allows tourists to construct convenient routes for visiting the Torgashinsky Ridge. There are 38 tourist objects in the system, and constructing any route takes an average time of 15 ms.