Метод акустической дифференциации наночастиц по размерам: современное состояние, численное обоснование

В последние годы наблюдается усиление интереса к позиционированию микро- и наночастиц на поверхностях, использованию для модифицирования известных материалов и создания новых. Позиционирование частиц на поверхностях включает в первую очередь область биосенсоров [1, 2] и молекулярной электроники [3, 4]. Для автоматизированного структурирования частиц существующие методы либо медленны [5, 6], требуют сборных моделей (например, путем электростатического позиционирования [7] или последовательной самосборки, передачи и интеграции [8]). Более того, сортировка частиц, органелл и клеток разного размера является важным для многих биологических и медицинских применений. Некоторые методы сортировки предлагают наибольший контроль процесса, но в автоматизированном виде, кажется, таких методов не существует.

Современные методы разделения частиц основаны на разности плотности и размера (размер – селективное осаждение [9], трещотки [10] и использование «эффекта бразильского ореха» [11, 12]), на разности поверхностных свойств (высокоэффективная жидкостная хроматография [13]), на разности заряда в зависимости от размера (гель-электрофорез [14]), на разности диэлектрической постоянной в связи с размером частиц (диэлектрофорез [15, 16]), а также на акустическом импедансе (ультразвуковое разделение [17]).

Что касается акустического разделения, то оно является новым и перспективным методом, однако использование этого способа для наноразмерных систем еще недостаточно изучено. Первые упоминания об использовании микрофигур Хладни для разделения нанодисперсных материалов содержатся в [18]. Обнадеживающие результаты по разделению нанопорошка диоксида кремния акустическим методом получены в [19]. Физически метод основан на аэродинамическом воздействии потоков газа (или жидкости) на частицы порошка. Сила воздействия потоков (сила Стокса) зависит от размера частиц, поэтому происходит их пространственное разделение. Основной механизм разделения связан с инверсными фигурами Хладни.

Классический способ визуализации стоячих колебаний – нанесение какого-либо порошка (обычно песка) на поверхность пластины, совершающей поперечные колебания под действием, например, смычка скрипки. При этом порошок образует картину, известную под названием фигур Хладни [20-22].

Намного менее известно то, что очень мелкий порошок скапливается в пучностях (в антиузлах) колебаний поверхности. Впервые это заметил Э. Хладни: тонкие волосы от смычка, которым он возбуждал колебания пластины, сосредотачивались на ней не там, где находился остальной порошок. Затем данное явление подробно изучил М. Фарадей с использованием спор плавуна (ликоподия) в качестве порошка [23]. Было показано, что движение мелких частиц к антиузлам вызвано циркуляционными потоками воздуха, вызванными колеблющейся пластиной [23-25]. Математическое объяснение этих воздушных потоков было сначала предоставлено Рэлеем [26, 27] и часто упоминается как акустическое течение. Однако этот последний термин является менее соответствующим для специфического течения, которое вызывает обратные фигуры Хладни, так как в данном случае сжимаемость воздуха не играет существенной роли. Поэтому ученые стали использовать термин «устойчивое течение» [28]. Формирование фигур на гибкой пластине – главный пример воздействия двух сил – силы Ньютона и силы Стокса: ньютоновы силы имеют тенденцию формировать классические фигуры Хладни, а силы Стокса имеют тенденцию образовывать обратные фигуры Хладни.

Именно свойство фигур Хладни пространственно разделять частицы на две фракции, различные по размеру, и используется в акустическом методе разделения частиц. Однако для эффективного использования рассматриваемого метода необходимо знать следующие параметры: частоту колебаний пластины, критический размер, при котором частицы попадут в другую фракцию (является функцией частоты), вязкость и другие параметры окружающей среды, амплитуду колебаний пластины и др. Решить эту задачу можно двумя способами: тщательными и длительными экспериментами или проведением численного моделирования.

В статье приведены основные результаты прямого численного моделирования [29], которое предоставляет нам детальную физическую картину взаимодействия воздуха и частиц на колеблющейся пластине.

Основы численной модели

Для моделирования исследователями [18] использована программа (код) «Комплексная дисперсная динамика» (Granular Dynamics – GD), вычисляющая гидродинамические силы. GD-код вычисляет траектории сферических частиц, исходя из закона Ньютона и учитывая взаимодействия частиц, которое дается трехмерной моделью столкновения сфер и учитывает тангенциальное трение. Код GD вычисляет параметры движения газовой фазы, оценивая уравнение Навье – Стокса конечным дифференциальным методом. Взаимодействие между малыми частицами и газом является двухсторонним и обрабатывается посредством эмпирического отношения перемещений. Взаимодействие больших частиц с газовой фазой осуществлено двумя способами, через метод сокращения ячейки и метод граничного погружения (МГП, имеется в виду граница между колеблющейся поверхностью и газом). МГП подтвержден тремя различными испытательными случаями, показывая, что он является универсальным.

Есть варианты описания газа в присутствии частиц, но их можно свести к двум типам: метод с полностью решаемым и с не полностью решаемым газовым потоком. Для полностью решаемого потока (моделирование решеткой Больцмана [30] или метод погружения границ [31]) газовая фаза решена в масштабе длины, которая намного меньше, чем размер частиц. Методы, полностью решаемые относительно газового потока, однако, очень требовательны к центральному процессору с точки зрения машинной памяти, и поэтому размер систем, которые могут быть изучены, ограничен, как правило, тысячей частиц для современных компьютеров. Для нерешенного потока газовая фаза решается в масштабе длин, больших, чем частицы (рис. 1), и поэтому требует меньших вычислительных ресурсов. Так как мы заинтересованы системами, большими, чем десять тысяч частиц, используем метод с нерешенным газовым потоком. В данном случае это необходимо, чтобы ввести эмпирические соотношения сил и принять во внимание взаимодействие газовой среды и частицы.

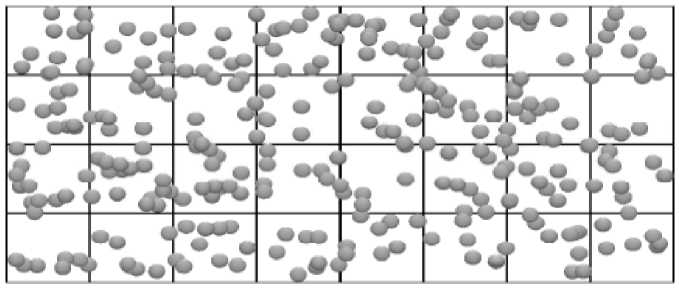
Рис. 1. Схематическое представление метода нерешенного потока;

газовая фаза решена при помощи вычислительной сети с масштабом длины, большим, чем размер частиц

Численная модель

Моделируемая система состоит из гибкой прямоугольной пластины размером 40×40 мм2, по которой однородно распределены 80 000 шариков с диаметром d = 0,075 мм. Пластина прикреплена вдоль ее внешней оправы. На высоте H = 2 мм над пластиной установлена защитная поверхность. Возбуждались 2 резонансные моды этой пластины. Пренебрегая изгибанием пластины из-за силы тяжести, вертикальное положение в любой точке (x, y) будет (рис. 2)

аемвивЯпЗм . -

/ (v, у, t) =---------sin 2яу

-1                                                                                                                         (1)

где ω = 2πf = 2π200 c-1 - резонансная частота пластины, α = 0,075 Мм – амплитуда колебаний и L = 40 Mм – ширина пластины.

Моделируемая система разделена на 60 ячеек вдоль каждой стороны пластины и 110 ячеек в вертикальном направлении, для того чтобы точно захватить слой выше пластины. Временной шаг, используемый для вычисления потока, равен 5∙10-5 c, таким образом, в одно колебание входит 100 временных шагов.

Рис. 2. Вид сбоку на гибкую пластину, резонирующую в 2× 2 модах. Вертикальное измерение увеличено в 40 раз

Сила воздействия газа на частицы может быть вычислена согласно закону Стокса:

F drag = 3πμd(u – v)                                          (2)

где μg – динамическая вязкость газа, u – местная скорость потока газовой фазы и v – скорость частицы. Отношение (характерной) силы Стокса и силы тяжести на частице тогда:

в _ Fares _ »^ad6i-v) l£^fiw y                                                                 (3)

Результаты моделирования

Если моделирование выполнено с золотыми частицами (ρ = 2000о кг/м³), отношение B будет приблизительно 0,03, то есть, движением частиц управляют ньютоновы силы. Из-за колебаний пластины частицы начинают подпрыгивать и (так как в большинстве случаев частица воздействует на область пластины, в то время как она перемещается вверх), последовательные прыжки имеют тенденцию увеличивать кинетическую энергию частиц. Однако в узловых линиях у пластины нулевая скорость и столкновения с ней уменьшают кинетическую энергию частиц. В результате, начиная со всех 80000 частиц, однородно распределенных по пластине, в течение нескольких секунд большинство из них скапливаются в узловых линиях, формируя стандартные фигуры Хладни (рис. 3 a).

Рис. 3. (a) Вид гибкой пластины, резонирующей в ее 2×2 модах, на которую были опрыснуты тяжелые частицы. После нескольких секунд большинство частиц собралось в узловых линиях, формируя классические фигуры Хладни. (b) Та же самая пластина с очень легкими частицами. Из-за присутствия воздуха частицы теперь мигрируют к антиузлам и после 4 с наблюдаются инверсные фигуры Хладни

Теперь уменьшаем плотность частиц до 20 кг/м³, держа постоянный диаметр. Это приводит к силе Стокса, которая почти в тридцать раз больше, чем гравитационная сила, действующая на частицу, то есть B ≈ 30. Это значение приблизительно то же, что и у порошка плауна (ρ = 46о кг/м³, диаметр d ≈ 0,016 мм [32]), который использовался Фарадеем в его экспериментах. Как может быть замечено на рис. 3 (b), эти легкие частицы перемещаются в антиузлы и образуют инверсные фигуры Хладни¹.

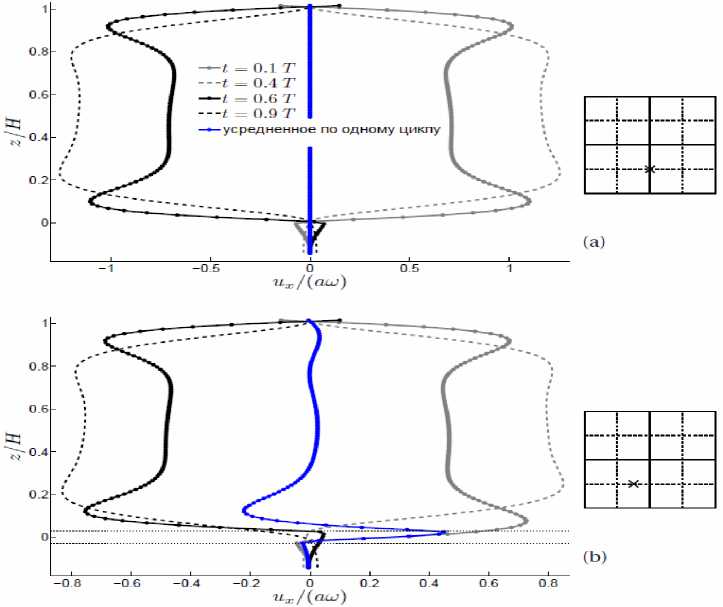
Рис. 4. Скорость как функция высоты в два разных момента – во время первой половины цикла (серые линии) и во время второй половины цикла (черная линия), и в двух разных местоположениях на пластине:

(a) в узловой линии (x = L/2 и y = L/4), и (b) на полпути между антиузлом и узловой линией (x = (3/8)∙L и y = L/4). Линия представляет амплитуду средней скорости по полному циклу колебания (увеличина в пять раз для наглядности). В местоположении (a) линия не отклоняется от нуля. В местоположении (b) есть устойчивое вытекание (линия отклоняется от нуля)

Очевидно, частицы не подпрыгивают на резонирующей пластине, так как движением частиц управляют силы Стокса. Кроме того, частицы следуют за движением газа. Физической причиной инверсных фигур Хладни является то, что циклическое движение газа (туда-сюда), усредненное по одному циклу, не является нулевым. Конфигурации, которые перемещаются синусоидально, могут произвести поток, который не является просто синусоидальным: в дополнение к поступательному движению газа туда и сюда есть устойчивое вытекание около поверхности вибрирующей поверхности [27, 28]. В момент времени t = 0∙ T у пластины нулевая скорость и максимальное ускорение. Пластина ускоряет газ около поверхности, и импульс газа впоследствии передается к более высоким слоям. После t = 0,25∙ T пластина замедляется и градиент горизонтальной скорости в граничном слое становится меньшим. Эта последовательность повторяется через половину цикла ( t = 0.5∙ T ), но в противоположном направлении, как обозначено на рис. 4a. На рис. 4 показана скорость в точке на узловой линии ( x = L /2, y = L /4) в двух моментах времени: в первой половине цикла (серые линии) и во время второй половины цикла колебания (черная линия). Ясно, что скорости во время обоих половин цикла аннулируют друг друга, поэтому средняя скорость в этой точке равна нулю. Другая ситуация в точке, находящейся посередине между антиузлом и узловой линией ( x = (3/8)∙ L и y = L /4), как показано на рис. 4 (b). Здесь пластина во время фазы ускорения первой и второй половины цикла находится в разном положении. В результате средняя скорость по одному колебанию не равна нулю и происходит устойчивый поток, который и приводит к инверсным фигурам Хладни путем воздействия потока (вихря) на частицы.

Помимо всего из модели путем использования обычной формулы Стокса для толщины граничного слоя была получена высота внутренней циркуляции (вихря)

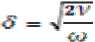
где ω – радиальная частота колебания, ν – кинематическая вязкость среды. Исходя из данного уравнения, можно вычислить частоту колебаний, необходимую для пространственного разделения наночастиц определенного размера. Так, при 20 нм она будет равна приблизительно 1,3 МГц.

Заключительные замечания

Рис. 5. Частицы на колеблющейся пластине с различным значением B (уравнение (3)), изменяемым в результате изменения плотности частиц. (a) силы Стокса доминируют, сформированы инверсные фигуры Хладни. (b, c, d, e) с постепенным уменьшением значения B мы видим постепенный переход к классическим фигурам Хладни. В (c) отношение силы Стокса и силы тяжести для частиц (ρ = 550 кг/м3) таково, что силы уравновешивают друг друга. В результате частицы не накапливаются ни в антиузлах, ни в узловых линиях.

(f) наконец для B = 0,03 ясно видно доминирование силы тяжести

Мы изучили формирование фигур Хладни на колеблющейся пластине прямым численным моделированием, включая поток окружающего воздуха. Чтобы кратко суммировать главные результаты, мы показываем на рис. 5 [29] полный переход между инверсными и классическими фигурами Хладни. Когда силы Стокса доминируют ( B > 1, ур. (3)), частицы движутся к антиузлам. Причина этого явления – это то, что движение окружающего воздуха, усредненного по одному циклу колебания, является отличным от нуля и очень легкие частицы следуют за движением воздуха.

Когда медленно увеличиваем плотность частиц (с шагом в 0,1% за одно колебание, позволяя системе приспособиться к новому условию), ньютоновы силы становятся более существенными и частицы начинают подпрыгивать, формируя облака вокруг антиузлов, которые становятся большими при увеличении плотности (рис. 5, b). Около B = 1 ньютонова сила и сила Стокса одинаковы, и облака покрывают почти всю пластину (рис. 5, c). Когда плотность увеличивается далее, ньютонова сила доминирует ( B < 1), приводя к классическим фигурам Хладни с частицами, накопленными в узловых линиях (рис. 5, f).

В реальном случае нет различий в плотности частиц, но за счет разности размеров мы имеем и разную массу частиц, так что механизм от этого не изменяется. Таков основной физический принцип акустического метода разделения частиц по размерам.