Метод аппроксимации петель гистерезиса многоконтактных виброизоляторов с сухим трением

мирования промежуточного приближения, можно осуществить переход от кусочно-полиномиальных функций к обычным алгебраическим многочленам.

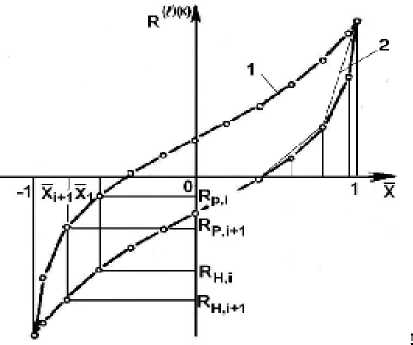
Простота и точность промежуточного приближения достигается применением сплайнов первой степени (рис. 1, 2) в сочетании с выбором определенного количества точек (от 10 до 30) и системы неравно отстоящих абсцисс x(^K ^ = x • А . Подобный выбор преследует основную цель: как можно полнее и достовернее отразить особенности процессов деформирования виброизоляторов [4, 5].

Запишем уравнение деформации для c отрезков процессов нагрузка и разгрузки K-ой петли гистерезиса семейства номера l rR №) + B(ЦЦ) (x - x ) vx(цц) > 0.

н, н, C I

R^ x-) + B p l c u) ( x - x ) v x ^(l)(K) <  0; (1)

R ( ^{l )}(^K) = _<  c

где B ( ¹ )( к) ^H, c

B ^{( l} )( ^k ) = ° p , c

n ( l )(K) _ n( l )(K) R H , I         ^R H , I + 1   .

;

x - x + 1

D ^{( l} )(^K) “ p , i

-

D ( ^l )( ^K)

^Rp ,i +1

x

-

x + 1

Причем для уменьшения погрешностей в определении полигональных функций, необходимо определить среднеарифметические значения R^l)(K), B^l)(K) и R ( )(K’ и B (1)(K) при дос-н , i              H , I                 p, i                p > c таточно большом количестве повторяемых измерений [6]. Вместе с тем при полигональной форме описания петель гистерезиса их площадь оказывается заведомо меньше искомой. Подобные проблемы могут быть в значительной мере решены выбором достаточно большого количества точек (например, в два раза по сравнению с вышеуказанным количеством), но значительного уменьшения повторяемых измерений.

При таком подходе уменьшение погрешности определения петель гистерезиса обеспечивается за счет описания их процессов нагрузки и разгрузки кусочно-линейными отрезками. Каждый из них доставляет равномерное приближение по Чебышеву на множестве из трех точек, последовательно следующих группами друг за другом (отрезки 2 см. рис. 1).

Тогда для каждых c ^* отрезков ( c ^*=0,5 с ) можно записать выражение (1) в виде:

R ^{( t}. ^)(K) =< c

'Riхю - внхю (x - -) vx(«ю > 0.

^ R j - в (j ) ( x - x j ) v x «кк) <  0; ⁽²⁾ где j О [0,2, … n -2];

x (R«хю + Rwoo  --A

R(l’(K) _ л    d(O(k) _ dW(k)\ h,l ^н,1+1     x+1

Rj    O--XM   RH,i  ) □ (1)(k) _ п(1)(к)   -- ;

V RH, i+2 RH,i      xi+t

R^{( 1 )( K)} _ R^{( 1 )(к)}

B Hj (K) = H, i  ^{Hi + 2} ;   v i _e [0,1,2... n - 2]

xi- xi+2

Изменяя индекс “н” на “р” IpICоpж:)но записать аналогичные выражения для R p j ^J и B p j .

Для решения задачи об интегральном аппроксимировании промежуточного приближения с помощью ортогональных полиномов необходи-

мо представить приближаемую функцию на единичных отрезках [1, -1] значений всех переменных. Это легко осуществляется с помощью соответствующих замен переменных A и q на Aq :

• - 2 A, . - A - A

• д - ^{(k) o} g л -² q⁸ q ° qv

• A^{1 1}’ " A g - a ° ^; q =^ v^ q ^ • ⁽³⁾

Точность аппроксимаций определяется выбором вида ортогональных многочленов.

Широкое распространение в задачах приближения получили ортогональные многочлены Якоби, частным случаем которых являются полиномы Чебышева и Лежандра [2]. Главное их отличие заключается в выборе вида весовых функций, что приводит в приближениях как бы к различному закону распределения погрешностей по длине отрезков [1,1]. При выборе весовой функции необходимо учитывать характер поведения приближаемой функции на отрезках [-1,1]. Нелинейность процессов деформирования виброизоляторов с сухим трением, в том числе и из материала МР в наибольшей степени проявляется на концах отрезков, где и требуется повышенная точность аппроксимаций. Таким свойствам обладают полиномы Чебышева. Заметим, что эти полиномы широко применяются для решения многих задач, связанных с вопросами виброизоляции [4, 7, 8]. Указанные обстоятельства позволяют выбрать полиномы Чебышева в качестве аппроксимирующих.

Рассмотрим вопрос об аппроксимации K -ой петли гистерезиса семейства £ в классе непрерывных и разрывных функций.

В первом случае необходимо, чтобы на множествах значений x было задано недостающее множество значений скоростей х(к^^[8]. Тогда задача интегрального аппроксимирования петли гистерезиса (3) полиномами Чебышева, обеспечивающими минимальную среднеквадратическую погрешность приближения при весовых функциях

f(X ’ =( V1 - X 2 )

Рис. 1. Построение промежуточного приближения контура петли гистерезиса (вариант 1)

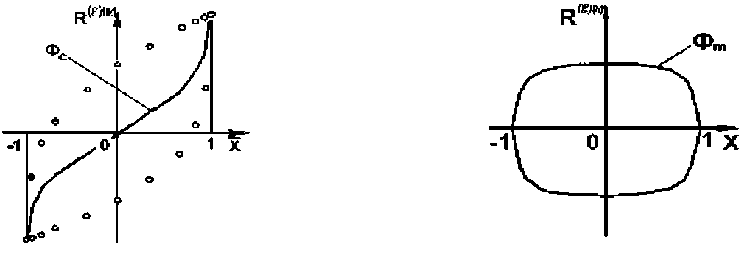
а ’                                                    б ’

Рис. 2. Построение промежуточного приближения петель гистерезиса (вариант 2): а – срединная линия; б – гистерезисная функция

и

f2( x ) =

(x 1 x)

- 1

, может быть сформули-

рована в виде

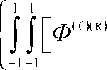
- Q ⁽ l ^)(к ) ] ² f ( x ) f 2 ( x ) dxdx \ . (4)

Здесь

m

Ф ⁽ l ^)(к ) ^ Q ⁽ l ^)(к ) = у p )) . x A x . 2 A^A^               (5)

I A= 0

разложение функции ф(l)(к) по полиномам Чебышева Q(1)(к) двух переменных x и x , причем Р.1.2 - коэффициенты Чебышевской аппроксимации и y (l)( к) _& x x = v(l)(K) ;

V ⁽1)(^к) — амплитуда скорости при циклическом деформировании. Установим ограничения, накладываемые на вид множества x ^{( l )(к}) .

При решении задачи об ( А ппроксимации в форме (4) коэффициенты р;^ вычисляются с помощью коэффициентов а . 1 . 2 разложения Фурье для двойного ряда.

4 ππ a/X'X' =—j j^Ф(l)(к)(cosф|,cosф2)cosX|ф| cosX2ф2 ]dф1 dф2 π 00

где ф 1 = arcos x , а ф ₂ = arcos x .

Для упрощения дальнейших записей индексы ( l ) и (к) будем опускать.

С помощью подстановки x" = cos ф 1 можно представить разложение петли гистерезиса в виде ряда Фурье из четных и нечетных слагаемых

где ст - ступенчатая функция.

При таком ограничении форма петли гистерезиса не зависит от скорости. При невыполнении условия (7) форма петли зависит от скорости x i .

С учетом соотношений (1), (7) проинтегрируем (6) и запишем

2 n ^ф >. = + ¹

a х,о =- Ё j⁽ R c ,н ⁺ R c , p ^)cos Хф 1 ^d ф 1 ;^{(8) п} -о ф;

4 X п n ^{ф |}’ i ^{+ 1}

a X 1 X ₂ = ,    ;^{sln 2} Ef ( R c ,н ^- R c , p ^{)cos Х} 1 ф 1 ^d ф 1 (9)

X-,П        2                                         ,

^{2                       1} = ⁰ ф 1, i

где l₁= 0,1,2,…, m ; l₂= m , m- 1,…,0; j_{1, i} О [0,p]; R_{c ,н} , R_{c , p} – соответствующие значения R_c для с -го отрезка ломанных.

В качестве примера приведем зависимости коэффициентов P _A 1 _A 2 от a _A 1 _A 2 при m =5 [8]:

^P 00    4 a 00   2 a 20

Pro 2 ^а ю 2 a

+— a, 2

^— ^ a 02 ⁺ a 22 ⁺ 4 a 04 ;

a 20    ⁴ a 40

30 ⁺ 2 a 50

^— a ₁₂ + 3 a 32 + a ₁₄ ^;

— 2 a ₂₂ ; P 30 = 2 a 30 — 10 a 50

P 40   ⁴ a 40 ; P 50   ^{8 a} 50 ; ^P 11    ^a 11    ³ a 31    ^{3 a} 13 ;

^{4 a} 32 ; (10)

P ₂₁ = 2 a ₂₁ — 8 a ₄₁ — 6 a ₂₃ ; P ₃₁ = 4 a 31 ; P ₄₁ = 8 a ₄₁ ;

m

ф = Е (aх1 cos Х1 ф1 + aх2 sin X1 ф1) .

I X | = 0

Здесь и далее индексы ( £ ) и (к) для упрощения записей исключаются, но при этом подразумевается зависимость функций и их коэффициентов от номеров семейств ( l ) и петель гистерезиса (к).

Введением новой переменной y = cos ф ₂

^P22   ⁴ a 22 • ^P 32 ⁸ a 32

;

Рассмотрим аппроксимацию петли гистерезиса с помощью полиномов Чебышева, представленных в классе разрывных функций. В этом случае форма петли гистерезиса описывается с помощью двух функций:

R = Ф c (x, A, q) + ст Ф m (x, A, q), причем первая из них описывает срединную линию петли гистерезиса (условную упругую составляющую), а вторая – неупругую составляющую (гистерезисную функцию) (см. рис. 2).

Эти функции можно представить в виде

Ф + Ф н р с ₂ ; m

Ф р

п

(где ф ₂ = ф 1 + "2" ), форму петли гистерезиса

Задачу интегрального аппроксимирования формы петли гистерезиса сформулируем в виде

можно описать только в классе ч е тных функций, но уже двух переменных x и y [4]. Следовательно, при разложении функции Ф по переменным x и x можно применять полиномы Чебышева первого рода, а коэффициенты разложения определятся с помощью (6), но при условии

min

min

x = у = СТ I V1 - x ² I -          ⁽⁷⁾

J (Фc — Qc )2 fx ( x) dx

— 1

J (Ф„ — Q. )2 f1 (x) dx

— 1

обеспечивающим наилучшее приближение раз-

дельно для функций Ф _с и Ф_m :

Ф ≅Q=m Pxλ1 Ф ≅Q=m Pxλ1 cc    cλ1  ; mm     mλ1

λ1=0

причем

R ≅ Qc+sQm.(12)

Коэффициенты P_{c λ 1} и P _{m λ 1} линейно зависят от коэффициентов a_{c λ} и a_{m λ} , которые вычисляются с помощью соотношений

• ₁    n ^ϕ 1, i + 1

a _{c λ} = ∑     ( R _{c ,н} + R _{c , p} )cos λ ₁ ϕ ₁ d ϕ ₁

π i = 0 ϕ 1, i

• ₁    n ^ϕ 1, i + 1

a _{m λ} = ∑     ( R _{c ,н} - R _{c , p} )cos λ ₁ ϕ ₁ d ϕ ₁

π i = 0 ϕ 1, i

В частности, для m=5:

a0P0=2 -a2+a4; P1=a1-3a3+5a5;

P2=2a2-8a4;P3=4a3-20a5;P4= 8a4; P5= 160a5.                  (15)

Таким образом, рассмотрены два варианта аппроксимации петли гистерезиса. Полученные соотношения (8), (9) для варианта (4) и (13), (14) для варианта (11) позволяют определять значения коэффициентов полиномов (10) и (15) для разложений (5) и (12), соответственно.

На рис. 3 в качестве примера представлены результаты аппроксимации петель гистерезиса для различных амплитуд прогибов виброизоляторов из МР типа ДК.

Сравнение экспериментальных данных с расчетными, полученными с помощью аппроксимирующих

RM

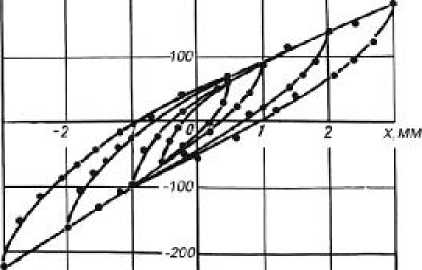
Рис. 3. Поле петель гистерезиса виброизоляторов типа ДК:

· – экспериментальные данные;

––– – результаты аппроксимации многочленов третьей степени (m=3), показало достаточно точное их совпадение при гармоническом законе изменения прогибов виброизолятора.