Метод деления на двоичную экспоненту для преобразования минимально избыточного модулярного кода в позиционный код

В настоящее время арифметика модулярных систем счисления (МСС) - модулярная арифметика (МА) активно применяется в цифровой обработке сигналов, обработке изображений, в спутниковых, сотовых инфокоммуникацион-ных системах, беспроводных сенсорных сетях, множественном доступе с кодовым разделением каналов, облачных вычислениях, в средствах обнаружения и исправления ошибок, контроля отказов и сбойных ситуаций, криптосистемах, других приложениях. Это обусловлено тем, что кодовый параллелилизм модулярных вычислительных структур (МВС) обеспечивает им ряд существенных преимуществ над позиционными структурами. Практическая реализация данных преимуществ в максимальной мере составляет определяющую стратегию всех проводимых разработок по МВС.

Чаще всего модулярные средства обработки информации используются совместно с позиционными. Поэтому эффективность МА-приложе-ний в значительной степени зависит от характеристик сложности и быстродействия применяемых методов и алгоритмов сопряжения разнотипных (по кодовой организации) компонент вычислительных систем, то есть средств позиционно-мо- дулярного интерфейса гибридных систем рассматриваемого класса. Представляемые в настоящей статье исследования относятся к проблематике оптимизации процедур образования кода МСС в позиционный код (ПК). Для решения проставленной задачи применен принцип минимально избыточного модулярного кодирования [1]. Ключевой отличительной особенностью минимально избыточных МСС (МИМСС) является использование так называемых интервально-индексных интегральных характеристик модулярного кода (МК), которые отличаются от известных характеристик - ранга, цифр полиадического кода и других [25] предельной простотой базовых расчетных соотношений. Фундаментальные преимущества интервально-индексной технологии синтеза алгоритмов модулярно-позиционного кодового преобразования далее наглядно демонстрируются на примере метода деления на двоичные экспоненты. Особое внимание при этом уделяется оптимизационным аспектам, охватывающим приложения МА на диапазонах больших чисел, и прежде всего криптографические МА-приложе-ния [6-12].

Принцип минимально избыточного модулярного кодирования

Введем обозначения:

• -    |_а_1 и М - наибольшее и наименьшее целые числа (ЦЧ) соответственно не большее и не меньшее вещественной величины a ;

• -    Z m = {0;1 ... m -1}, z; ={-Lm/2j; -Lm/2>1; ... Гrn/21 -1} - множества вычетов по натуральному модулю m ;

• -    A |m - элемент кольца Z _m , сравнимый с A (в общем случае рациональным числом) по модулю m ;

• - M = {mi;m₂ ... m^ - базис МСС, состоящий из k>1 попарно простых модулей тц »?2 ... пн-

• В МСС с базисом M ЦЧ X представляется кодом (хйх2 ... XkXli ^ПЦ; 1 = 1,^). Максимальная мощность множества DMcc чисел X, на

котором отображение ^(ХьХ2’-’Ха-) взаимно к однозначно составляет Мк =Пт/ элементов.

В этом случае Омсс выполняет роль диапазона МСС. Обычно в качестве диапазона используют ^м_к или ^м_к •

Из Китайской теоремы об остатках следует, что ЦЧ ХеОмсс может быть получено по своему МК (ХнХ2,-,ХаЭ с помощью равенства x^m^Jm^A ^Мк_хЦХу (1)

А-1

где ^Mi, k-i = ^мк-\^z »ч;      и к -1 = П ^mj ’

№ = I_kQ^ – интервальный индекс (ИИ) числа X [1]. Выражение (1) называется интервально-модулярной формой (ИМФ) ЦЧ X .

При | DМСС | = Mk МСС с базисом M является неизбыточной. Между тем использование в системах счисления кодовой избыточности, как правило, позволяет существенно улучшить их арифметические и иные свойства [1; 7-9]. Так называемое минимально избыточное модулярное кодирование: ®МИМСС ^ ^m, Х^т. Х "■У''^тк предусматривает применение диапазона DМИМСС, мощность которого меньше мощности диапазона DМСС неизбыточной (классической) МСС с базисом M. Сущность реализуемого принципа рас- крывает нижеследующее утверждение.

Теорема 1.Оминимальноизбыточноммодулярном кодировании. Для того, чтобы в МСС с попарно простыми основаниями пц; m2 … каждого элемента _¥=(X1’X2’-’Xa)   диапа- зона Z2A/- {-M-M+l м- \у где

М = т₀М_к__х; т₀ - вспомогательный модуль, полностью определялся компьютерным ИИ – вычетом 4Ш = |/Ш| , необходимо и достаточно, чтобы k -ое основание удовлетворяло условию:

т_к > 2.т₀ + к — 2 (то ^ к — 2). При этом для I ( X ) верны расчетные соотношения:

_ Л W если 1 к Ш < то;

.1 к (^) - тк ^ если !к Ш ^ то;

Kxviyxv

jLRi,M

К1,кАхд =

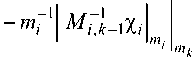
RkAZk) = \MA-lXk\ ■

U * к),

Переход от МСС с базисом Ми Z^ к МИМСС с тем же базисом и диапазоном ^2M предельно упрощает базовой интегральной характеристики модулярного кода (ИХМК) – ИИ I ( X ) согласно (2)-(4)). Это приводит к адекватной оптимизации и немодульных процедур, базирующихся на ИМФ (1). Количество необходимых таблиц и модульных операций для таких процедур при расчете базовых ИХМК сокращается в k /2 раз [1-2]. С увеличением мощности рабочего диапазона МИМСС получаемый выигрыш становится особенно значимым.

Формализация метода деления на двоичную экспоненту для преобразования минимально избыточного модулярного кода в ПК

Пусть в МИМСС с базисом М и диапазоном ^2M задано число X = (Хь X2 ■■■ Xa) и пусть требуется получить его представление в ПСС с основанием r – дополнительный r-ичный код (•^/г-1^7-2-" Xo)r ^xj G ^r U = O’" “!)) длины n. Необходимым условием корректности преобразования (Хь X2, •■■, XA-) → ^n—X'^n—'l*** ^^r является включение диапазона

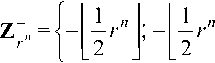
^1M МИМСС в диапазон

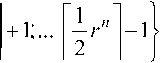
ПСС.

Из отношения Z2M cz Z^_„ вытекает неравенство 2Л/ <  r" . Следовательно, дополнительный r -ич-ный ПК должен иметь длину (»>riog,.(2M,)l) цифр.

Поскольку компьютерная позиционная арифметика ЦЧ, в частности в персональных ЭВМ, фактически представляет собой арифметику по модулям вида 2^b ( b = 8; 16; 32; 64), то в качестве основания базовой ПСС целесообразно использовать re{2⁸ , 2¹⁶ , 2³² , 2⁶⁴}. Нетрудно видеть, что вычисление выражений вида (1) с использованием (2)-(4) по указанным модулям r в рамках применяемой таблично-сумматорной технологии осуществляется весьма просто.

Благодаря реализационным преимуществам ИМФ (1) и отмеченному обстоятельству преобразование МИМК в ПК эффективно может быть выполнено методом деления на двоичную экспоненту – основание r ПСС. Представляемый метод преобразования кода МИМСС в дополнительный r -ичный ПК базируется на операционном кортеже рекурсивного типа:

(Л =x, -r₀ н^о I,-; ^1=И *1 =1^11,-;

x. = к /'"J; x, =| x₂1,. x_n__x = L^-2 /rj; (5)

На j -ой итерации процесса реализации (5) сначала формируется минимально избыточный модулярный код (МИМК) (zP izVV--, z^) ЦЧ Xj, а затем находится цифра x_j его дополнительного r -ичного ПК путем расширения полученного МИМК на модуль r согласно правилу

*и wb^I^^ и

+1 М_к__хКХ^ I,. I,.(7=0, /7-1).

Что касается числа X_j , то в соответствии с (5) для цифр его МИМК верна формула

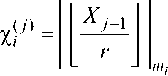
Xi при 7 = 0;                             (7)

I I/P⁴* - ^_i I™, ' I r"* L, I™, при у = 1, n -1;

(z = l, ky

Конкретный выбор способа компьютерной реализации расчетных соотношений (6)-(7) рассматриваемого метода кодового преобразования в первую очередь определяется величиной основания r ПСС. Если r = 2 ⁸ или r = 2 ¹⁶ , то вычисление выражений (6) с использованием (7) в рамках таблично-сумматорной технологии, предполагающей ограничение модулей m_i МИМСС порогом m_max = 2 ¹⁶ (m_i< 2 ¹⁶ U-^кП наиболее про сто и эффективно осуществляется с помощью таблиц TMpl_ i модульного умножения на константы C,=\r"^A |_m и таблиц TE_ i расширения МК. Необходимые таблицы генерируются по правилам:

TMplJ [x] =1 С,x \_m. (Z = 0, mj -1; z = 1Д-); (8) ^_i\%\=\M_ik__v\M7^A_k__v%\_mi\_r-, ^ = 0,т₄-\И = \,к-ХУ (9) TE_£[x] =

\Mk-\X\r при z = 0, 7И₀-1;

----------- (10)

J M_k__x (/ - m_k ) I,. при x = т_й, m_k - 1.

Расчетное соотношение (10) базируется на формуле (2) для ИИ ЦЧ в МИМСС. Аргументом таблицы TE_ k при фиксированном j служит компьютерный ИИ Z = ^_v) числа X_j – см. (6). Для вычисления ЦХ^ воспользуемся таблицами ИИ – TII_ i , в которых хранятся наборы вычетов вида (4) согласно правилу

TH j [x] = Ri,_k (X) (z = 0,777,-1; 7 = ij) • (11)

С учетом (11) из (3)-(4) для компьютерного ИИ 4(^y) следует расчетное соотношение

1кЛху =

Етп-^хр)]

Таблично-сумматорная технология предполагает получение модульных сумм (12) аккумулятивно-табличным методом [10]. Это требует использования еще двух таблиц:

TRes_UP^[.r] = | 2¹⁶x |,„_t (x = 0, 2¹⁶ -1),

TRes£[.x] =| x |„_;< (x = 0, 2¹⁶ + m_k — 2)

для приведения ЦЧ к остаткам по модулю m_k .

Таблично-сумматорная алгоритмизация схемы деления на двоичную экспоненту для преобразования МИМК в ПК

Из изложенных базовых положений метода деления на двоичную экспоненту и принципов его компьютерной реализации вытекает нижеследующий алгоритм преобразования кода МИМСС в ПК.

Параметры алгоритма: модули m\, m^, ..., m_k МИМСС, выбираемые из множества простых чисел промежутка (2 ¹⁵ ; 2 ¹⁶ ) с минимизацией k [10], и основание r = 2 ^b ( b =16 бит) используемой ПСС.

Входные данные алгоритма: МИМК (Zb Z2i … произвольного элемента X диапазона ^2M ^.

Выходные данные: дополнительный r -ичный код ^n—V^n—1 ’" ^o)f длины 77 = ri0g,.(2Afk ЦЧ X .

Предварительно полу ча емые данные: константы Ci=\r"^AL U = U1, а также таблицы TMplJ, TEJ, TIIJ (7 = Ц), TRes UP^- и TResA-– см. (8)-(11) и (13).

Тело алгоритма модулярно-позиционного кодового преобразования по методу деления на основание ПСС с применением таблиц расширения МИМК.

МП_Д.1. Положить

^0 1X1 ’X2 ’’"■’ Xx- ) (Xl’X2'>""’ Xk ) •

МП_Д.2. Порядковому номеру очередной цифры дополнительного r -ичного кода ЦЧ X присвоить начальное значение j = 0.

МП_Д.3. В соответствии с (6) с помощью таблиц (9), (10) расширить МК (Xi^^X^’"-’ x/ ) числа X_j (см. (5), (7)) на основание r ПСС, выполняя операции:

МП_Д.3а. Применяя таблицы (11), вычислить входящую в расчетное соотношение (12) сумму

^ЕТП,/^] .

МП_Д.3б. Получить компьютерный ИИ ЦЧ X_j , приводя s к остатку по модулю m_k согласно правилу

i(Xj) =| s |_m< = TRes£[?⁰⁾ + TRes UPA^v"¹JJ (s^,0) = = sa(2¹⁶T), s⁽¹⁾ =s»16.

МП_Д.3в. Вычислить j -ую цифру дополнительного r -ичного ПК входного числа:

Xj =1 2ТЕ _/[xp") ] + ТЕ _ Wj )] I,. (14)

/=1

МП_Д.4. По достижении равенства j = n – 1 завершить работу алгоритма.

МП_Д.5. Инкрементировать переменную j ( j = j + 1).

МП_Д.6. Следуя (7), сформировать МИМК (xp\ X<2 ’•••’ x^) числа Tv-L^/rJ, реализуя для всех i = 1, к операционную последовательность:

МП_Д.6а. Найти x = xV ¹⁾-^₇-1-

МП_Д.6б. Если X < 0, то положить X = X + m, .

В противном случае – перейти к МП_Д.6г.

МП_Д.6в. При x < 0 текущее значение переменной X нарастить на m, {х = Х + т^.

МП_Д.6г. Из таблицы TMpl_ i (см. (8)) по адресу X искомое значение i -ой цифры МК числа X;. Xp^TMplJtx].

МП_Д.7. Перейти к МП_Д.3.

Для временных затрат на выполнение в ПЭВМ модулярно-позиционного кодового преобразования с помощью процедуры МП_Д.1–МП_Д.7 справедлива оценка:

^мпjj-пэвм (А л) - 2(26/? - 6 -и)1сл +

+ (k(n-\) + 5n)t4,

где ten И t₄ – длительности операций сложения и чтения двухбайтового слова из таблицы соответственно.

Объем памяти для таблиц, используемых в алгоритме МП_Д.1–МП_Д.7, не превышает

3 ^Тт.мпл^“T^ + ^ M5.

Предположим, что полумощность M диапазона МИМСС удовлетворяет условию M >2 ¹⁰²⁴ . В этом случае минимальное число k оснований базиса M принимает значение k = 65 [10]. Согласно теорем е 1 2m₀< m_k - к + 2. Поэтому ввиду пт, < i" U -^k) неравенство 2M обеспечивающее минимум разности rⁿ – 2M, достигается при n ≤ k. Пусть n = k = 65, тогда оценочные выражения (15)-(16) в случае t_сл = 2 нс, t_ч = 1,14 нс дают: ^?мп_д.пэвм(65,65) - 38392,9 нс, ТАт мп_д ⁼ 24,75 Мб.

Приведем оценки (15)-(16) для еще одной конфигурации алгоритма МП_Д.1 – МП_Д.7, которая определяется условием M >2 ²⁴⁶² . Отвечающая данному равенству МИМСС имеет k = 155 оснований; и при n = k = 155, t_сл = 2 нс, t_ч = 1,14 нс искомые значения характеристик (15)-(16) составляют: ^мп_дпэвм(155,155) - 219055,3 нс, А/_{т мп}_д = 59,5 Мб.

Пусть теперь re {2³² , 2⁶⁴}. Так как в этом случае цифры r -ичного ПК (х,,.^,,^... х₀\. достаточно велики, то при реализации (7) они должны быть преобразованы в остатки по модулям m _i . Для выполнения операции Т-1 * I ^Х /-1 Im воспользуемся представлением ЦЧ ^xj-\ ^G ^r в ПСС с основанием r =2^b (6=16 бит):

_r №-24 (0).

E (l) ~l (0) , ~z (1) , ~z (и-2) ,

Х ДГ = X + Г + Г (...Г (X\₄  + (17)

/=0 '

+ ?(.х⁽Д7¹⁾))...)) ^-b/b;x\'l_vez~).

Вычисление выражений вида (17) по модулям m_i весьма просто осуществляется с помощью таблиц

TRes _ UP/[x] = | rx \_m_, TRes/[x] =| x |_w

(x = 0, /■ + m_t - 2); i = 1, k).

Искомое расчетное соотношение для остатков %р-пН^-1 ц, базирующееся на (17)-(18), имеет вид

xP"n =

TRes/fx^ + TRes^P/fx^J], если r = 2³²,

= < TRes/fx^

+ TReS-UP/ExV], + TReS-UPztx^ +

+ TRes_UPz[Xy^1]]]], если z-= 264,

(z = 1^).

Поскольку с увеличением разрядности p основания r используемой ПСС длина n кода (x„_]X„_₂... x₀)_r уменьшается, причем достигаемое за счет этого сокращение временных затрат на преобразование МИМК в ПК при достаточно большом r становится более значимым, чем их возрастание, обусловленное выполнением операций (19), то с точки зрения проблемы повышения скорости процедур модулярно-позиционного кодового преобразования рассматриваемого класса весьма эффективным является с овместное использование таблиц TE_ i (z = U) расширения кода и ПСС с большими основаниями.

Модификация алгоритма преобразования МИМК в ПК, реализующая обозначенную концепцию, заключается в нижеследующем.

Параметры алгоритма: модули m ₁ , m ₂ , ..., m_k базовой МИМСС, основание r =2 ^b 12 64}) используемой ПСС и основание r =2⁶ (b =16 бит) ПСС для представления цифр дополнительного r -ичного ПК.

Входные данные алгоритма: МИМК (xi; X2;

... xO ЦЧ xиз диапазона Z;w .

Выходные данные: дополнительный r -ич-ный код ^n— 1^?2— 1"' ^o)r длины ZZ = Plog,.(2jW)^ числа X.

Предварительно получаемые данные: таблицы TMplz, TEz, TII_z, TRes_UPz и TResz G = U), формируемые согласно (8)-(11) и (18).

Тело алгоритма модулярно-позиционного кодового преобразования с применением таблиц расширения МИМК на модули r разрядностью b =32, 64 бита.

_МП_Д.1. Положить

^0 1X1 ’%2 ‘" X^ / vXl’X2 *■■ ^Lk,

_МП_Д.2. Порядковому номеру очередной цифры ПК числа X присвоить начальное значение: j =0.

_МП_Д.3. С помощью соотношения (6) и таблиц (9), (10) расширить МИМК (xP ;хз7 •■• xp )

числа Xj (см. (5), (7)) на основание r ПСС, выполняя операции:

_МП_Д.3а. Применяя таблицы (11) и (18), вычислить компьютерный ИИ HXj) ЦЧ x_h определяемый по расчетному соотношению (12), согласно схеме:

/ к                                               ~

/ s = ^ТП-ЯхР¹]; x⁽⁰⁾ = x a (r -1), s^¹* =s»b;

\     *=i

UXj ) =| 5 |_m< = TRes£[x⁽⁰⁾ + TRes_UP£[s⁽¹⁾]]\.

_МП_Д.3б.   Найти   j -ую   цифру ПК

(x^X^-.-Xo),. исходного ЦЧ X по правилу:

xv.=|ZTE_z[Zp)] + TE_^[/(X/)]|,..

/=1

_МП_Д.4. При j = n –1 завершить работу алгоритма.

_МП_Д.5. Переменную j увеличить на 1 ( j = j +1).

_МП_Д.6. Согласно (7) сформировать МИМК

(xPP xPP..., xpP числа Xj=\x_HlA реализуя для z = l,k действия:

_МП_Д.6а. По формуле (19) выполнить преобразование x_H -^ (xp ^U.

_МП_Д.6б. Найти X Xz Xz ‘ .

_МП_Д.6в. Если x < 0, то положить X = X + 114 ■

_МП_Д.6г. Получить искомое значение i -ой цифры МИМК числа Xj. xP^TMpijM.

_МП_Д.7. Перейти к шагу _МП_Д.3.

При реализации на ПЭВМ алгоритм _ МП_Д.1–_МП_Д.7 требует временных затрат

¹ МП Д.пэвм(^^и^) - ^,7(^сл ⁺⁴⁷ч +2yZ, b

+ 7сл (^) + (^ - 2) max   ?ч ^сл W } ) +

+^("-1)(^П0(^) + 2?сл +гч), где tч– время чтения двухбайтового слова из таблицы; tсл (b) – время сложения двух b-битовых ЦЧ; tсл =tсл (32); tПО (b) – длительность операции приведения к остатку цифры r-ичного ПК по модулю mi М = ^к) МИМСС. Из (19) следует, что

^по(^)- "

t„„ + 2/„ при b = 32 бита,

Р ,                           (21)

3?_сл + 4/_ч при b = 64 бита.

Быстродействие современных схем сложения несущественно зависит от разрядности b . С учетом этого положим ^сл(^) ^сл-

Пусть b = 32 бита, а мощность диапазона ^IM МИМСС удовлетворяет условию 2M > 2∙2 ¹⁰²⁴ . В этом случае k = 65, n = 33 и оценка (20) с учетом (21) при t_сл = 2 нс, t_ч = 1,14 нс принимает значение ^?_мп_д.пэвм (65,33,32) - 28990,68 нс. В случае, когда b = 64 бита, 2M > 2 ¹⁰²⁵ , длина r -ичного ПК составляет 17 цифр и 1_мпл-пэвм (65,17,64) = 236883 нс. Если мощность диапазона МИМСС удовлетворяет условию 2 M > 2∙2 ²⁴⁶² , которому отвечает k = 155, то при b = 32 бита длина r -ич-ного ПК составляет n = 77 цифр и ^?_мп_д.пэвм (155,77,32) = 162554,52 нс. В случае, когда b = 64 бита, код ПСС с основанием r =2 ⁶⁴ имеет длину n = 39 цифр и ^?_мп_д.пэвм (155,39,64) = 132384,04 нс.

Объем табличной памяти для алгоритма _ МП_Д_1–_МП_Д_7 не превышает

Мт мп_д(^,6) = ^ • 217(6 + 6/16) байт. (22)

Для пар ^,6) = (65,32); (65,64); (155,32); (155,64) оценка (3.61) принимает значения:

Мт._мпл (65,32) = 65 Мб;

М_т._мпл(65,64) = 81,25 Мб; М_т__мп_д(155,32) = 155 Мб; M_T__Mnjl(155,64) = 193,75 Мб.

Приведенные оценочные данные по производительности и суммарному объему табличной памяти для приведенных конфигураций алгоритмов преобразования МИМК в ПК по методу деления на основание r ПСС позволяют заключить, что с ростом r четко просматривается тенденция к увеличению скорости осуществляемого преобразования. При рассматриваемых значениях параметров k и b (£е {65, 155}, be {16, 32, 64}) характер и уровень достигаемого повышения производительности наглядно иллюстрируют коэффициенты:

^,мп_дпэвм(65,65,16)/ /__мп_д_пэвм(65,33,32) = 1,3; ^,мп_дпэвм(65,65,16)/ ^_мп_дпэвм(65,17,64) = 1,6; ^мплпэвм (155,155,16) / ^_мплпэвм (155,77,32) = = 1,35;

^мплпэвм (155,155,16)/ ^мпл.пэвм (155,39,64) = = 1,7.

Благодаря возможности применения принципа обобществления таблиц при формировании базового КТ системы, что допускает использование одних и тех же таблиц разными немодульными процедурами, сопровождаемое отмеченный рост быстродействия алгоритмов модулярно-позиционного кодового преобразования, увеличение объема необ- ходимой табличной памяти фактически оказывается несущественным и для МА-приложений вполне приемлемо.

Заключение

Наиболее значимые результаты представленной разработки по оптимизации методологических и алгоритмических средств модулярно-позиционного кодового преобразования кратко можно охарактеризовать следующим образом.

• 1.    Проведена математическая формализация метода деления ЦЧ в МСС на двоичную экспоненту, который положен в основу процедур модулярно-позиционного кодового преобразования. Главной отличительной особенностью реализуемого подхода при синтезе процедур исследуемого класса является применение минимально избыточного модулярного кодирования. Это позволяет сократить объем табличной памяти и временные затраты, приходящиеся на вычисление базовых интегральных характеристик МК в k /2 раз .

• 2.    Синтезированы два новых алгоритма модулярно-позиционного кодового преобразования. Один из них ориентирован на ПСС с основанием r = 2 ¹⁶ , а другой – на ПСС с основаниями r = 2 ³² и 2 ⁶⁴ . Алгоритм с r = 2 ¹⁶ прост в реализации, но формирует ПК максимальной длины. С увеличением r количество цифр ПК уменьшается . При этом, однако, в реализуемом вычислительном процессе на каждой итерации выполняется операция приведения последней полученной цифры ПК к остаткам по модулям МСС, что снижает производительность соответствующего алгоритма.

• 3.    Исследована эффективность компьютерной реализации рекурсивной схемы деления на основание ПСС в рамках двух стратегий, первая из которых предполагает расширение МК преимущественно с помощью системных средств, а вторая с использованием таблиц расширения. Анализ разработанных конфигураций процедур преобразования МИМК в ПК с точки зрения проблемы повышения производительности при установленном верхнем пороге для размера табличной памяти показывает, что оптимальный результат достигается в случае совместного применения таблиц расширения и ПСС с большими основаниями r . При r = 264 получаемый выигрыш в быстродействии (в сравнении r = 2 ¹⁶ , 2 ³² ) является (1,3-1,7)-кратным.