Метод диагностики состояния лесов, подвергнувшихся антропогенному воздействию

DOI:

Введение. Известно, что леса играют важную роль в регулировании биосферных и атмосферных процессов, представляя собой своеобразное пристанище биоразнообразия на Земле [1; 2; 4; 5–7; 9; 11; 13; 17]. При этом антропогенный фактор значительно воздействует на жизнь лесных участков и их экосистемную роль. Одним из широко распростра- ненных видов воздействия человека на леса является фрагментация лесов, осуществляемая в виде рубки деревьев и оказывающая непосредственное влияние на биоразнообразие лесов [3; 8; 10; 14; 16], а также на их структуру, в особенности в крайних участках лесных массивов [12; 15; 18–20]. С ростом фрагментации лесов их способность регулировать

глобальное энергетические и гидрологические циклические процессы ослабляется. Процессы фрагментации лесов неизбежно воздействуют на природные процессы формирования и/или восполнения пустых участков, существующих в лесных массивах. Фазовая динамика изменения таких пустых участков, в свою очередь, оказывает некоторое воздействие на развитие лесов и содержит значительную информацию об общем состоянии леса. В настоящей статье предлагается метод оценки информативности дистанционного определения степени антропогенного воздействия на лесные массивы по признаку выявления и определения частотности появления пустых участков в лесах.

Предлагаемая модель статистических свойств появления больших пустот в лесном покрове. Предлагаемый метод оценки информативности дистанционного зондирования. Частотное распределение пустот в общей кроне лесного покрова определяется показательным законом распределения плотности вероятности [13]. Согласно этому закону плотность вероятности f ( s ) определяется как

- λ f ( S )= ^S ζ(λ)^,

где S – размер пустого участка; λ – параметр распределения; ζ ( λ ) – дзета функция Римана.

Также используется модель, где показатель λ является функцией расстояния d от конкретной рассматриваемой точки в лесном массиве до края этого массива [16]. В этой модели

λ=β 0 +β 1 ⋅ е ^{- β 2} log 2 d , (2)

где β ₀, β ₁, β ₂ = const .

Вместе с тем при исследовании динамики образования больших пустот в лесах из-за природных факторов, а также антропогенной деятельности выяснилось, что выражения типа (1) в принципе не соблюдаются [14]. Пустоты крупного размера имеют логнормальный закон распределения (рис. 1).

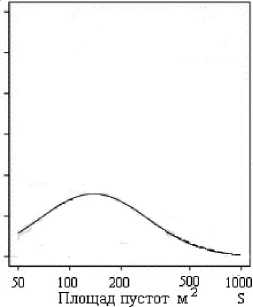
Pис. 1. Плотность вероятности распределения больших пустот, образовавшихся в лесах [14]

Нами предлагается зонально-негомогенная равновероятная модель появления пустых участков в лесах. Эта модель основывается на следующих положениях:

– лесной массив состоит из множества L , включающего n количество подмножеств L_i , i = 1, n . В каждое подмножество L_i входят лесные зоны D_{i, j} , j = 1 , m_i , содержащие пустоты размером S_i . В каждой такой зоне находится всего лишь один пустой участок;

– допускается, что в участках, входящих в подмножество L_i , плотность вероятности распределения размеров участков подчиняется равномерному закону, при этом размер участка может изменяться в пределах 0 ÷ S_i ;

– несмотря на равномерный закон распределения размеров пустых участков в пределах каждого подмножества L_i , в целом в переделах множества L закон распределения оказывается трапециодальным, что иллюстрируется на рисунке 2.

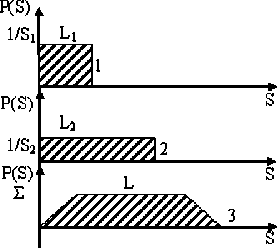
Рис. 2. Иллюстрация формирования трапециодального закона распределения элементов множества L , состоящего из двух подмножеств L ₁ и L ₂. (В переделах L ₁ и L ₂ соблюдается равномерный закон распределения соответственно S ₁ и S ₂)

Допускается, что при большой величине n общий вид закона распределения P ( S_L ), где S_L – элемент множества, L приближается к функции распределения, показанной на рисунке 2.

Вышеуказанные положения позволяют нам построить следующую информационную модель взаимосвязи частотности появления пустых участков и их размеров. Применительно к подмножеству L_i информация, содержащаяся в получаемых при измерениях данных, определится как

S

M ( L i ) = m i' log 2 A S ,               ⁽³⁾

где A S - квант измерения площади пустот; m i - количество проводимых измерений в подмножестве L_i .

Суммируя (3) по всем i , получим n

M(L) = £ m' log2 ,<.

i=1

Выражение (4) в непрерывном виде запишем как max

M ( L ) = j m • log ₂

S dS .

A S

Введем на рассмотрение функцию m = p( S).

И далее осуществим переход от m к показателю частотности f(s) с помощью равенства m = k • f (S), где k = const.(7)

Таким образом, с учетом (5)–(7) получим

S max

M (L) = j kf (S) • log2 AS-dS.

Полученная формула (8) позволяет оценить информативность результатов дистанционного зондирования состояния лесов по признаку статистики выявленных пустот в лесных массивах. Для выяснения экстремальных свойств данной информационной оценки проведем модельное исследование с учетом известной закономерно- сти взаимосвязи частотности пустот и их размеров.

Модельное исследование. Существует фактическая линейная убывающая зависимость между логарифмической величиной частотности появления пустых участков заданного размера log₂ f ( S ) и логарифмом размеров участков log₂ S [14] . На рисунке 3 приведен линейно аппроксимированный вид экспериментальных данных [14], полученных при наблюдениях на уровне высоты крана 20 м, где X = 1,74; n = 439 ( n – количество картированных пустых участков).

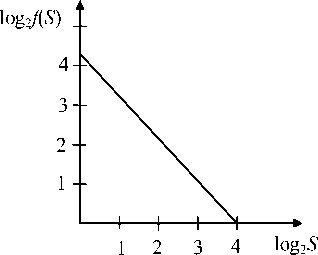
Рис. 3. Линейная аппроксимация зависимости log₂ f ( S ) от log₂ S , где f ( S ) – частотность появления пустого участка с размером S

С учетом графика, представленного на рисунке 3, можно составить следующее ограничительное условие:

max

J [ log 2 f ( S ) - k , log 2 S ] dS = C ,          (9)

где С = const, k ₁ = const .

С учетом выражений (8) и (9) составим вариационную задачу безусловной оптимизации:

S max

M0(L) = fkf (S) • log2 — dS -0          A S max

-Y j [ log 2 f ( S ) — k i log 2 S ] dS ,

где у - множитель Лагранжа.

Согласно методу Эйлера оптимальная функция f ( s ), приводящая функционал (10) к экстремальному значению, должна удовлетворять условию

C            Sr                    Л d|kf(S)10g2 AS - Y[log2 f (5) - k1 log S]|

df ( S )

= 0.(11)

С учетом выражений (11) получим

k • log, —= 0.

² A S f ( S )

Из выражения (12) имеем

f (S ) =

γ.

^k l^og 2 A S

С учетом выражений (9) и (13) получим

s max

log ₂

( k log2 S V      AS 7

- k i log 2

dS = C .

обнаружения и изучения статистики пуcтот в лесных массивах.

Алгоритм предлагаемого метода может быть изложен в следующей последовательности:

• 1.    Составляется множество

• 2.    Последовательно вычисляются значения функционала:

• 3.    Определяется i , при котором

• 4.    Проверяется предикат

Z = { f ( S ) } ; i=Гп .

M ( L ); i = 1, n.

f , ⁽ S ) =^ min.

Очевидно, что выражение (14) позволяет вычислить значение у. Не вдаваясь в подробности такого вычисления, полученное значение множителя Лагранжа обозначим как у0. В этом случае из выражения (12) имеем f (S ) =----Y ,                 (15)

k • log, —

² A S

Таким образом, при существовании зависимости между частотностью появления f ( s ) пустот размером S и показателем S в виде (15) функционалы (8) и (14) достигают экстремума.

Для нахождения типа экстремума достаточно вычислить d2 j kf(5)log2    - Y[log2 f(S)- ki log 2 S]

L^A S

f ( S ) =----.               (17)

k log

• ^{6    2} A S

• 5.    Если условие (17) выполняется, то выводится заключение о наличии в лесном массиве пустот антропогенного происхождения; в обратном случае считаем, что таких пустот нет.

Блок-схема алгоритма предлагаемого метода показана на рисунке 4.

Заключение. Используя полученные результаты анализа информативности, можно предложить практическое правило для обнаружения факта наличия пустот антропогенного происхождения в лесных массивах методом дистанционного зондирования. Так как: (a) оценка информативности дистанционного зондирования в виде выражения (5) верна только для случая наличия двух подмножеств L ₁ и L ₂ (рис. 1); (b) подмножество L ₁, характеризующее множество пустот естественного происхождения, существует почти всегда; (с) при наличии подмножества L ₂, характеризующего множество пустот антропогенного происхождения, функционал (8) с учетом выражения (15) будет достигать минимума, то критерием обнаружения пустот антропогенного характера можно принять факт достижения минимума функционалом (8) только при использовании функции (15) для вычисления численных величин M ( L ).

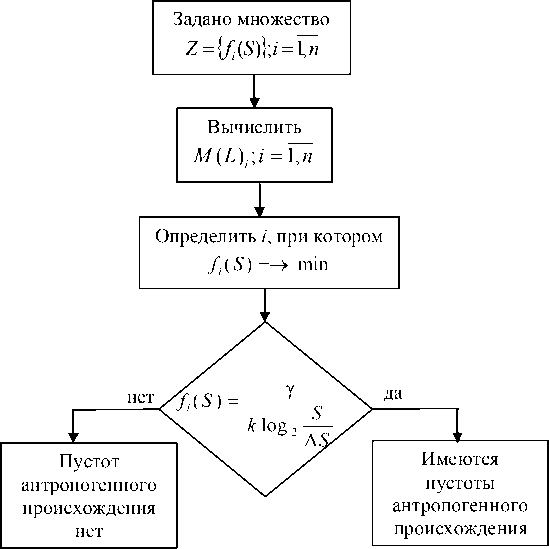
Рис. 4. Блок-схема алгоритма предлагаемого метода