Метод достижения максимальной дифракционной эффективности голограмм на основе оптимизации формфактора

При разработке новых голографических материалов большое внимание уделяется увеличению динамического диапазона фотоотклика среды [1, 2]. Однако влияние фактора формы голограммы может существенно ограничивать достижимые значения дифракционной эффективности голограмм несмотря на достаточно большие значения динамического диапазона фотоотклика голографического материала [3 –6]. Причиной этого является наличие перекрёстного взаимодействия двух факторов – нелинейности отклика на экспозицию и неравномерности самих голограмм по полю, проявляющееся как формфактор голограмм.

Традиционно формфактор в физике и геофизике – это функция, описывающая влияние протяжённости частицы на её взаимодействие с другими частицами и полями [7, 8]. Упрощённо – это поправочный коэффициент в формуле взаимодействия точечных частиц, приводящий к правильному вычислению взаимодействия тел сложной формы или взаимодействию тел с неоднородными полями. Здесь мы употребляем термин формфактор по аналогии с классическим, имея в виду, что основной «силовой» параметр голограммы – её дифракционная эффективность, может упрощённо вычисляться введением в классическую формулу Когельника [9] простого поправочного коэффициента ψ, заранее вычисленного для голограмм разной формы. Учёт такого коэффициента похож на учёт поправочного коэффициента (формфактора) для гравитационной постоянной G (или константы другого взаимодействия) в зависимости от формы тела c учётом нелинейного отклика (в формуле гравитационного взаимодействия – это (1 / R2). Далее мы увидим, что полученный формфактор ψ вырождается при отсутствии любого из двух факторов – либо нелинейно- сти, либо неоднородности пучков. В отсутствие любого из них он утрачивает своё значение.

В настоящей работе показана связь величины формфактора и максимально достижимой дифракционной эффективности голограммы. Предложены методы снижения влияния формфактора и увеличения средней дифракционной эффективности голограмм.

В работе показано, что с увеличением диаметра голограммы по отношению к размеру площадки голографического материала максимально достижимая дифракционная эффективность увеличивается. Это показывает, что в предельном случае прямоугольных по яркости пучков мы получаем известный результат [9], для которого формфактор равен единице.

В работе также предложен метод уменьшения влияния формфактора путём изменения по полю голограммы её видности, например, с помощью изменения взаимной когерентности записывающих пучков или отношения их интенсивностей.

Численное моделирование и экспериментальные результаты

Влияние формфактора определяется, во-первых, неоднородностью яркости объектного и опорного пучков по полю голограммы, что связано не только с неоднородностью яркости голографируемых объектов, но зачастую имманентно присуще неоднородности самого лазерного излучения, имеющего Гауссов вид, а во-вторых, – нелинейностью формирования фотоотклика. Действительно, нелинейность присуща не только насыщающемуся с ростом экспозиции фо-тоиндуцированному изменению показателя преломления A n для фазовых материалов и фотоиндуциро-ванному изменению показателя поглощения для амплитудных [10– 13], но и самому способу формирования фотоотклика в виде дифракционной эффективности объёмных голограмм [9]:

П = sin 2 ( aA n ). (1)

Здесь α (определён в [9]) – коэффициент, зависящий от углов падения записывающих, восстанавливающих пучков и толщины голографической среды.

Даже на линейном участке формирования фото-индуцированного отклика ∆ n зависимость дифракционной эффективности голограммы η (её фотоотклика на экспозицию) нелинейна и имеет синусоидальный вид (1). При этом более яркие участки голограммы (у голограммы, записанной Гауссовыми пучками, это её центральная часть) скорее достигают максимально возможной η при α∆ n = π/2, а её края ещё только подтягиваются к максимуму.

А когда они достигают своего максимума, яркие участки голограммы уже свой максимум преодолели и их локальная η снижается.

На рис. 1а – в в виде трёхмерных фигур показано распределение локальных значений дифракционной эффективности по полю Гауссовой голограммы для трёх дискретных значений экспозиции. Видно, как центральная часть голограммы переходит максимум (очевидно, при α∆n = π/2), затем как бы проваливается, затем повторно достигает максимума, а периферия голограммы отстаёт в своём вкладе в среднее значение дифракционной эффективности. Уже здесь, по рис. 1, можно понять, что среднее значение дифракционной эффективности η никогда не сможет достигнуть максимума, достижимого по формуле (1) её центром при экспозиции, соответствующей в центре α∆n = π/2. Соответственно, при желании увеличить ̅η за счёт увеличения экспозиции мы рискуем получить нелинейные искажения в центральной части голограммы. Это тем более опасно, что мы увидим эти искажения не сразу, а только после преобразования скрытого изображения в процессе проявления. Так можно, не учитывая «форму голограммы», не догадываясь об этом, ухудшать отношение сигнал/шум, записывая всё более «яркие» голограммы, но всё более «зашумлённые». Фактор влияния этой формы на среднюю дифракционную эффективность определяется вычислением интегрального значения η для голограмм каждой определённой формы.

П = ^ | ^ jj sin 2 { P ( E ) E ( x , У )V ( x , У ) } d x d У , (2)

где β( E ) – голографическая чувствительность фотоматериала, E ( x, y ) – локальное значение экспозиции по полю голограммы и V ( x, y ) – распределение видно-сти, зависящее в общем случае от комплексной степени когерентности и локального соотношения опорного и объектного пучков при записи голограмм.

Как показано в [3, 4], в большинстве случаев сложное для практического использования выражение (2) можно с достаточной степенью точности заменять на (3).

n = Q sin² { T f ( EV ) } , (3)

где T - константа, характеризующая распределение яркости записывающих и восстанавливающего голограмму пучков по её полю или, другими словами, форму голограммы.

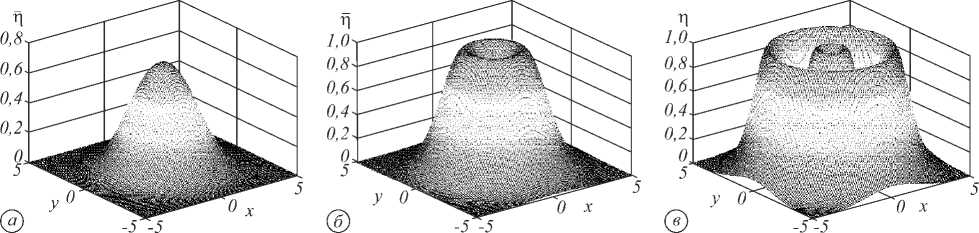
Рис. 1. Распределение локальной по полю голограммы дифракционной эффективности, записанной Гауссовыми пучками, при α∆n=(0,8)π/2 (а), α∆n=1,2π (б), α∆n=5π/2 (в)

Отметим, что в нашем случае формой голограммы, очевидно, является не её апертура (круглая, квадратная и др.), а трёхмерная фигура, где по двум осям координат отложена яркость восстановленного голограммой пучка. Такую константу можно вычислить для каждой голограммы, записанной Гауссовыми и не Гауссовыми пучками. Величина достижимой дифракционной эффективности Ω не поддаётся аналитическому вычислению, однако, определяется формой голограммы или её формфактором и может быть получена численно для каждого вида голограмм. Например, для наиболее интересного – Гауссова вида на рис. 2 приведены численные расчёты по (2), где β( E ) предполагается линейной.

Видно, что кривая 1 первого локального максимума, соответствующая не Гауссовой, а некой иде- альной, плоской, с равномерной засветкой голограмме, рассчитанная по (1), достигает при α∆n = π/2, а кривая 2, рассчитанная по (2), отстаёт примерно в 1,6 раза (для удобства сравнения амплитуда кривой 1 на графике уменьшена в 3 раза по сравнению с расчётной). Можно сказать, что для вычисления оптимальной экспозиции «Гауссовых» голограмм можно использовать известную для плоских голограмм экспозицию и, умножая её на коэффициент ψ =(1 / 1,6) ≈ 0,6, находить оптимальную экспозицию из (4).

Тв EV = п /2.                             (4)

Здесь E – экспозиция, рекомендованная по ТУ [14], β – голографическая чувствительность фотома- териала. Параметр ψ, который будем называть формфактором голограммы, определяет снижение её средней дифракционной эффективности в зависимости от формы голограммы и вида нелинейности отклика. Здесь под откликом понимается не только формируемый при экспозиции фотоотклик голографического материала, но и связанная с ним дифракционная эффективность полученной голограммы. Выражение (4) вместе с вычисленным Ω, упоминаемым в (3) как коэффициент снижения максимального значения средней дифракционной эффективности голограммы, полностью задаёт практически нужные характеристики голограммы. Величины ψ и Ω позволяют качественно, по-новому понять ограничения, связанные с формфактором голограммы. Последний из этих параметров, определённый из модельных расчётов по (2), (рис. 2), как Ω ≈ 0,26, объясняет, почему в экспериментальных работах [9, 11, 13] не была, да и не могла быть достигнута высокая дифракционная эффективность голограмм. Это позволяет понять, что поиск голографических сред с большим динамическим диапазоном фотоотклика уже не даст дальнейшего увеличения дифракционной эффективности.

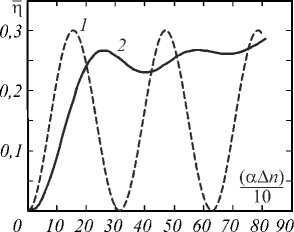
Рис. 2. Средняя дифракционная эффективность

̅η голограммы Гауссовых пучков (кривая 2) для случая линейного фотоотклика в сравнении с дифракционной эффективностью плоских, равномерных пучков (кривая 1)

На рис. 3 отчётливо видно, что, действительно, как мы и предполагали, с увеличением средней экспозиции голограммы её дифракционная эффективность с какого-то момента уже не растёт, а приходит к насыщению (кривая 2). Одновременно её наиболее яркая часть (в случае Гауссовых голограмм – центральная) уже перевалила за максимум и ускоренно воспроизводит нелинейные искажения, которые при α∆ n = π становятся уже существенными.

При введении нелинейности фотоотклика, аналогичной измеренной экспериментально в [15], вычисления по (2) дают для ̅η почти такой же вид зависимости от экспозиции, но по величине существенно меньшей, чем при линейном отклике (рис. 3). По-видимому, это связано с тем, что к моменту достижения дифракционной эффективностью первого максимума (при ψα∆ n = π/2) чувствительность фотоматериала из-за нелинейности фотоотклика голографического материала падает примерно в той же пропорции.

Следует отметить, что средняя дифракционная эффективность ̅η зависит, согласно (2), не только от экспозиции, но и от распределения видности записываемой интерференционной картины по полю голограммы.

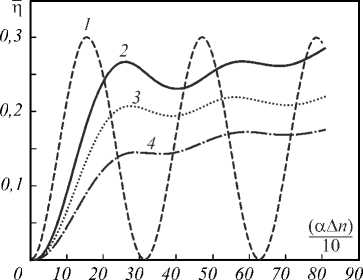
Рис. 3. Средняя по полю дифракционная эффективность ̅η голограммы световых пучков для случая линейного фотоотклика (кривая 2) в сравнении со случаем нелинейного фотоотклика (кривая 3) для случая нелинейности, хорошо аппроксимирующей экспериментально найденную у фазового голографического материала «Реоксан» [11], и (кривая 4) для вдвое большей нелинейности

Видность при этом – дополнительный свободный параметр, который определяется не только соотношением интенсивностей объектного и опорного пучков ( I a / I r ), но и распределением по полю голограммы комплексной степени когерентности γ ar [3].

V = 4 ( U, ) 2( Y ., 1 * [2 ( I . + 1 , ) ]) =

= 2IY „I

( 1 .1 1 , У + ( 1 ,1 1 . )

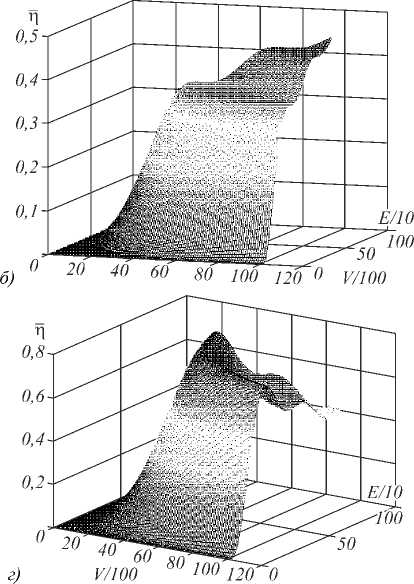
При этом и E и V симметрично влияют на величину фотоиндуцированного фотоотклика среды ∆ n . А значит, следует учитывать распределение по полю голограммы не только экспозиции, но и качества интерференционной картины, достигшей фотоматериала при записи голограммы. На рис. 4 показаны зависимости ̅η от экспозиции E и видности V для голограмм, записываемых Гауссовыми пучками разной ширины.

Приведённая на рис. 4 а зависимость η ( E ) соответствует кривой 2 на рис. 2. Видно, однако, что изменения V могут корректировать значения η при фиксированной экспозиции E .

Также на рис. 4 б – г видно, что с ростом экспозиции после определённого момента η не только не увеличивается, а даже начинает падать.

Гауссовы голограммы на рис. 4 имеют ширины, определённые по уровню 1 / e . От рис. 4 а к рис. 4 г дальние, неяркие края такой голограммы всё более существенно выходят за поле голографического материала и возникает новый эффект, связанный со всё большей равномерностью экспозиции по полю голограммы, чем при чистом Гауссе.

Именно этот эффект приводит к снижению дифракционной эффективности голограммы после достижения первого максимума, как это происходит на кривой 1 рис. 3. То есть можно сказать, что рост вклада в дифракционную эффективность краёв голограммы с ростом экспозиции замедляется виньетированием свободного поля зрения или виньетированием зрачка оптической системы, которую представляет голограмма. Однако, как видно из рис. 4в и г, пройдя максимум по E, можно снова вернуться к нему, уменьшая V, что открывает новые возможности для оптимизации параметров записывающего голограмму излучения. Как видно из выражения (5), зависимость V(γar, Ia, Ir,) не очень простая и даёт возможность для творчества в поисках оптимальных по полю голограммы значений γar, Ia и Ir . Например, при простом уменьшении видности за счёт уменьшения γar в центральной части Гауссовых пучков, записывающих или восстанавливающих голограмму, можно получить большие значения ̅η, чем при больших γar . Как это ни парадоксально звучит на первый взгляд, но средняя дифракционная эффективность Гауссовых голограмм может достигать более высоких значений при провале степени когерентности излучения в центре голограммы. Этот эффект не вполне осознанно нами использовался в [13, 15], где в некоторых случаях для записи голограмм или восстановления использовалась лазерная мода ТЕМ 01*, или «бублик».

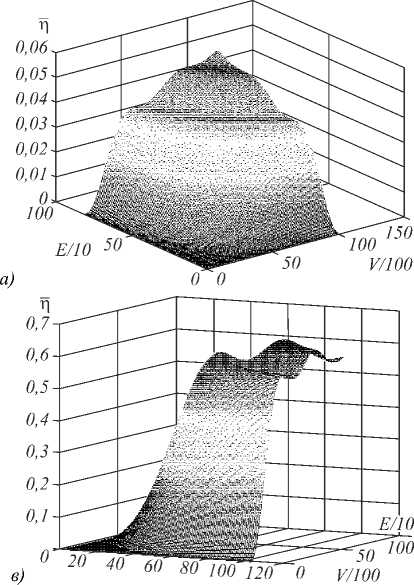
Рис. 4. Зависимость η от E и V для случая узкой, по сравнению с полем голографического материала, голограммы.

Их линейные размеры в данном случае относятся как 1 : 5, и краевые эффекты при этом слабы (а); зависимость η̅ (EV) для соотношения линейного размера голограммы к линейному размеру голографической среды 3 : 5 (б); зависимость ̅η (EV) для соотношения линейного размера голограммы к линейному размеру голографической среды 4 : 5 (в); зависимость ̅η (EV) для соотношения линейного размера голограммы к линейному размеру голографической среды 1 : 1 (г)

Обсуждение результатов

В работе видно, что, когда радиус пучка меньше размеров площадки, где записывается голограмма (рис. 4), эффект влияния формфактора сказывается в полной мере, и с ростом произведения EV появляется почти плоская поверхность, слабо, мелкими шажками (через каждые π /2) прирастающая вверх. В этой ситуации, следуя экспериментальным измерениям ̅η, легко ошибиться и продолжать увеличивать экспозицию, хотя понятно, что наступает опасная область взрывного роста всяческих шумов [9] и нелинейных искажений. Но когда размер пучка становится сравним с размером площадки голограммы или больше, зависимость η уже больше напоминает классическую (1) или (3) с ψ = Ω = 1.

Также из полученных в работе результатов видно, что нелинейность фотоотклика вместе с неравномер- ностью экспозиции голограммы по полю голографического материала (определяющая формфактор голограммы) существенно ограничивают предельно достижимую дифракционную эффективность (пропорционально Ω) и снижают эффективную чувствительность (пропорционально ψ). Становится очевидно, что стандартное решение – поиск голографического материала с большим динамическим диапазоном фотоотклика – не принесёт желаемого результата – увеличения дифракционной эффективности голограмм. Для этого нужно выбирать другой путь.

Во всех рассмотренных на рис. 4 случаях видно, что недостаток локальных E можно компенсировать ростом локальных значений V. Обратное тоже верно. Переход через первый горб (где выполняются условия (4)) на графиках (рис. 4) приводит к неоправданному росту шумов, что должно быть подробно рассмотрено в дальнейшем. Достижение этого горба очень многовариант- но. Это и локальные по полю голограммы изменения E и V, зависящие от Ia+ Ir ; Ia/ Ir; γar , и меняющаяся в процессе записи чувствительность голограммы, хотя бы из-за нелинейности её фотоотклика, а также различные фазовые рассогласования интерферирующих пучков в процессе записи [11 – 13]. Всё это позволяет надеяться на то, что реализация таких условий записи, следовательно, и высокоэффективных голограмм, аналогичных плоским, Когельниковским (рис. 1), в том числе и динамических, не за горами.

Другими подтверждениями многовариантности и принципиальной реализуемости создания похожих условий является и широко известная неравномерная по полю модовая структура обычных лазерных пучков, и появление в последнее время совершенно новых структур лазерного излучения [16].

При исчезновении любого из двух эффектов (нелинейности, либо неоднородности) формфактор вырождается. В случае отсутствия неоднородности просто ψ = 1, а в случае отсутствия нелинейности (что может быть верно только для тонких сред на начальном этапе экспозиции и в случаях, когда нет эффектов перекачки из объектной в опорную волну и обратно) график зависимости η ( E ) становится линейным и нет того горба, как на рис. 2, 3, по которому мы определяем оптимальное значение экспозиции и величину ψ (конечно же, в настоящей работе пока в отсутствие шумов). Следовательно, между нелинейностью и неравномерностью существует перекрёстное взаимодействие, порождающее возникновение эффекта, описанного нами как формфактор, и этот эффект существует только тогда, когда присутствуют эти оба фактора одновременно.

Распределение локальной дифракционной эффективности по полю голограммы меняется с экспозицией так, что центральная часть голограммы, записываемая наиболее яркими частями пучков, быстрее достигает Когельниковского максимума и затем «проваливается» в соответствии с формулой (1) и рис. 2, 3. Края голограммы при этом ещё только подтягиваются к локальному максимуму η. Понятно, что средняя дифракционная эффективность голограмм сложной формы растёт уже не по формуле Когельни-ка, а сложнее. Удачно, что этот рост можно было увидеть в модельных экспериментах, результаты которых показаны на рис. 1 –4, и выделить в них первую ступеньку, когда средняя дифракционная эффективность η достигает первого максимума. Из анализа этой кривой, точнее, из положения этого максимума, и делается вывод о величине поправочного коэффициента ψ =(1 / 1,6) ≈ 0,6, позволяющего на практике пользоваться не сложной формулой (2), а простой формулой (3). Можно считать удачей, что этот первый максимум, определяемый формфактором голограммы, остаётся хорошо выраженным и легко определяемым.

Поиск аналитического выражения для вычисления формфактора голограмм не был задан в настоящей работе, хотя, несомненно, является интересным, по- скольку, если нет явной формулы для вычисления формфактора, то это ещё не значит, что его нет. Он есть, он был обнаружен, и его влияние при записи голограмм бывает катастрофично. Максимально достижимая дифракционная эффективность уменьшается на порядки (рис. 4а). Это в некотором смысле подарок природы, что такой неподдающийся ранее фактор найден, т. к. он зависит не от одной причины, а проявляется только при одновременном наличии двух причин одновременно – нелинейности отклика и неоднородности яркости. В остальных случаях он не виден. Именно поэтому он долго и не был обнаружен. Однако в природе он присутствует всегда, поскольку голограммы всегда имманентно нелинейны, а лазерное излучение имманентно неравномерно. Попытки уменьшить влияние формфактора выравниванием яркости пучков по полю (рис. 4б – г) приводят к существенным потерям мощности в пучках [7] и усложнению аппаратуры, что иногда просто неприемлемо, как, например, в голографических запоминающих устройствах (ГЗУ).

Влияние формфактора на достижимую дифракционную эффективность не ограничивается Гауссовой формой записывающих пучков. В соответствии с (2) можно вычислить формфактор ψ для любых пучков, однако можно полагать, что в соответствии с ЦПТ теории вероятности, распределение ярких и неярких участков голограммы сложных пучков, например, изображений реальных объектов и даже портретов, будет также приближаться к Гауссовому, а, значит, полученый выше параметр ψ≈ 0,6 может иметь более широкое, чем только для Гауссовых голограмм, применение.

Заключение

В работе приведены результаты расчёта формфактора для объёмных фазовых голограмм. Показана его зависимость от типа (формы) голограммы и вычислены конкретные значения для Гауссовых голограмм. Также показано, что с увеличением влияния формфактора, выражающегося снижением значений ψ ниже единицы, уменьшается (пропорционально Ω) величина максимально достижимой дифракционной эффективности голограмм. Определена величина Ω для случая Гауссовых голограмм. Показаны пути уменьшения влияния формфактора на максимально достижимую дифракционную эффективность, в т. ч. изменение по полю голограммы видности γar и соотношения интенсивности записывающих голограмму пучков Ia/ Ir. Показано, что влияние формфактора проявляется только при одновременном существовании двух факторов – нелинейности отклика, в данном случае η (E, V), и неравномерности яркости по полю E (x, y). В отсутствие любого из них влияние формфактора вырождается, и средняя дифракционная эффективность определяется классическими выражениями [9]. На основе полученных в работе результатов сделано предположение о более широкой применимости вычисленных для Гауссовых пучков значе- ний ψ ≈ 0,6 и Ω ≈ 0,26, а именно: применимости для всех диффузных пучков, имеющих Гауссову статистику яркости по полю. Последнее носит характер постановки задачи для дальнейших исследований.