Метод фазового пространства в анализе статистики флуктуаций оптических импульсов в нелинейных диспергирующих средах
Автор: Широков С.М.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Компьютерная оптика: Дифракционные оптические элементы, технология и приложение
Статья в выпуске: 14-15-2, 1995 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14058302
IDR: 14058302
Текст статьи Метод фазового пространства в анализе статистики флуктуаций оптических импульсов в нелинейных диспергирующих средах
Процессы распространения сверхкоротких световых импульсов в нелинейных диспергирующих средах привлекают в последние годы возрастаю щи й интерес в связи с возможностями их использования для передачи с особо высокими скоростями, создания элементов оптических компьютеров, новых оптических приборов и т.п. [1-3]. По мере уменьшения длительности импульсов в таких оптических системах все более важное значение приобретает учет флуктуаций источника излучения, снижающих степень его когерентности. Знание статистики флуктуаций необходимо для выбора алгоритмов обнаружения, различения и фильтрации сигналов в указанных системах, а также оценки их характеристик [4, 5]. Хотя задачи анализа флуктуирующих сигналов в нелинейных средах исследованы уже довольно подробно, для их функций распределения известны лишь отдельные результаты статистического моделирования на ЭВМ и качественные оценки применительно к некоторым упрощенным моделям среды передачи [3, 6-9]. Ниже предлагается общий подход к решению указанных задач, основанный на представлении модели оптической среды (канала передачи) в гамильтоновой форме относительно некоторых обобщенных фазовых координат.
-
2. Постановка задачи
Процессы нелинейного самовоздействия сверхкоротких световых импульсов в нелинейных диспергирующих средах описываются волновыми уравнениями, которые в рамках дисперсионного приближения второго порядка по методу медленно меняющихся амплитуд после соответствующей нормировки обычно допускают представление в виде нелинейного эволюционного уравнения шредингеровского типа (НУШ) [1, 3]
/—+а—^+/рф+ко|ф|2ф = О (1)
ди от с начальным условием ф(0,т)=5(т), (2)
где т], т - нормированные координаты (пространственная и временная, отсчитываемая от Центра движущегося импульса); ф(г|,т) - комплексная огибающая импульса излучения, нормированная на начальное пиковое значенеие; s(t) - входное воздействие; а, р, к0 параметры дисперсии, затухания и нелинейности (ко<0 соответствует нормальной, а ко>0 - аномальной дисперсии).
Модель (1) обладает большой универсальностью, позволяя описывать не только процессы распространения оптических импульсов в одномодовых волоконных световодах, плоских пленочных волноводах и открытой среде, но и электромагнитные волны СВЧ в нелинейных средах, волны в плазме и даже некоторые виды акустических волн.
С учетом флуктуаций излучения входное воздействие (2) представляется в виде 5(т)=«(т)ц(т)+^(т) (3)
Где и(т) - детерминированная комплексная функция, определяющая форму и фазу импульса на входе, ц(т) и ^(т) - комплексные случайные процессы, отражающие мультипликативные и аддитивные флуктуации излучения. Их статистические характеристики, а тем самым и характеристики всего воздействия (3), включая многомерные функции распределения, будем считать известными.
При этих условиях необходимо установить закономерности, которым подчиняется эволюция функции распределения флуктуирующего сигнала в рассматриваемой нелинейной среде по координате т|.
-
3. Метод фазового пространства
Существует класс систем, для которых решение поставленной задачи может быть получено в весьма общем виде. К этому классу относятся системы, уравнения динамики которых допускают представление в гамильтоновой форме относительно некоторых обобщенных фазовых координат. Чтобы получить такое представление для уравнения (1), введем новую функцию
\р(т|,т)=<р(пт)еР11(4)
относительно которой оно приобретает вид
^+ос^+к(т])|\р|2у=0 ,(5)
где
к(т])=к0е-2Рт1 ...(6)
В качестве фазовых координат здесь целесообразно выбрать вещественные функции -квадратурные компоненты х(т|,т), Хп^) комплексной огибающей
^(л^хСп^+гИп^) .(7)
После подставновки (7) в (5) получается система из двух вещественных уравнений, которые можно представить в виде дх ЬН дуЬН
5q 5 у 5q5х где Я(х^) - гамильтониан, определяемый выражением
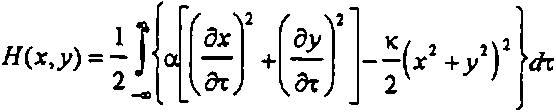
Аналогичные комплексные уравнения можно записать, выбрав в качестве фазовых переменных \р(т],т) и ц/*(л,т) [10].
Полученные уравнения (8), в отличие от аналогичных уравнений, рассматриваемых в статистической механике [11], описывают распределенную динамическую систему с бесконечномерным фазовым пространством и поэтому содержат в правой части не обычные, а вариационные производные (по функциям континуальной переменной т ). При случайном входном воздействии с заданным функционалом плотности вероятности ^o(x,y) его эволюция в системе, описываемой гамильтоновыми уравнениями (8), подчиняется уравнению Лиувилля [11], которое в рассматриваемом фазовом пространстве также должно быть записано с использованием вариационных производных:
где
8W , .
---+{Я,^} = 0 , dq
{wrM
5/7 8FK 8Я 5^ by bx bx by
скобки Пуассона.
Уравнение (10) можно получить также из функционального уравнения Фоккера-Планка-Колмогорова [12], положив в нем коэффициенты диффузии равными нулю.
4. Решение с использованием дискретизации по времени
Непосредственное использование уравнений в вариационных производных типа (10) и описываемых ими функционалов плотностей вероятностей для анализа характеристик нелинейных оптических систем затруднительно, так как такие функционалы допускают строгое определение лишь в классе обобщенных функций. При практическом анализе и моделировании на ЭВМ функции х(т|,г) и уОъД как правило, дискретизуются по т с некоторым шагом Ат и представляются векторами отсчетов
где N - число отсчетов,
Дл^^о^), ^(лХ-лы-Кп)], Д^Ьъ (^^(nX-^.i^)],
^(п)^, (£-Л/2)Дг), Ук(п)=У(л, (£--№)Дт); £=0,1,2,...,ЛЧ.
Полученные в результате такого конечномерного представления случайные векторы X, Y описываются обычной 2Л^-мерной плотностью вероятности И^Х, У,т0, а скобки Пуассона в (10) приобретают вид
где гамильтониан
У Г дН dW дН дУ Z!\5ykdxk дхкдук>
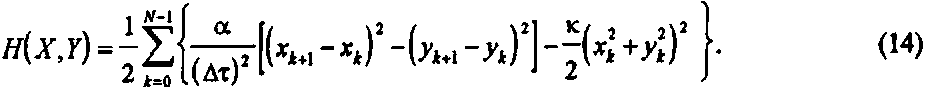
После подстановки (14) в (13) и простых преобразований уравнение Лиувилля (10)
принимает вид
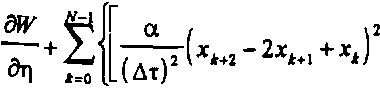
+ti +У>к
0W а
8ук .(Ат)2
(yM-2yM+yJ +кк+у»)у* г-
Решая его при начальном условии
ДДУО) = >^О(ДУ),
где w0(X,Y) - плотность вероятности квадратурных компонент входного воздействия, методом характеристик, получаем общее выражение 2У-мерной плотности вероятности векторов отсчетов Дт|), Дц) в произвольной точке л :
ДДУ^-^т/Д!)] (17)
Здесь Ь\ (X,Y) - оператор нелинейного отображения вход-выход, определяемого уравнением (5) при заданном и с учетом дискретизации (12); * - знак сопряженного оператора. При выводе формулы (17) учтено, что НУШ вида (5) относится к классу уравнений с унитарной нелинейностью [13], поэтому обратный оператор может быть заменен сопряженным.
Как в теоретическом, так и в практическом отношении большой интерес представляет вопрос о существовании стационарных распределений, не изменяющихся при преобразовании (17), а также равновесного распределения, к которому стремится ДХУл)
при неограниченном увеличении 0т|. Согласно выводам статистической механики [11] свойством стационарности обладает любая начальная плотность вида wo(^,y) = №,!)] (18)
где I(X,Y) - какой-либо интеграл движения рассматриваемой системы, например, гамильтониан. Для рассматриваемой системы в случае ее линейности (к=0) гамильтониан (14) представляет собой квадратический функционал и стационарным является гауссовское распределение с определенной корреляционной матрицей, которую легко найти из (14). Однако, если при этом в начальном воздействии (3) «(т) не является константой, распределение wo(X, У) не может быть стационарным.
Ненулевые состояния статистического равновесия в рассматриваемой системе возможны только при отсутствии потерь 09=0) и характеризуется равномерным распределением по эквиэнергетической поверхности (микроканоническим распределением Гиббса) с заданным значением гамильтониана Н(Х, У)=Я0,
^хда^^сцн^жх^А (19)
где С - нормирующая константа.
В условиях флуктуаций входного воздействия флуктуирует и Яо с некоторым распределением м<Яо), которое может быть найдено по известному распределению woQC,Y) . При этом равновесное распределение следует определять по формуле
«ДХ/О-ЬУ^ДХ/ЦН^аН. (20) о
В отличие от задач статистической механики, где изменения Но обусловлены термодинамическим взаимодействием с внешней средой, в данном случае распределение w^H^ не обязательно является экспоненциальным и поэтому w (Л,У) не совпадает с каноническим распределением Гиббса. Для реальных начальных распределений wo(X10 расчет wp(X,Y) описанным методом, как правило, приводит к распределениям, не выражающимся через элементарные функции и допускающим только приближенные или численные представления.
Равновесное распределение, как легко видеть из (19) и (20), определяется только функционалом H(X,Y) и не зависит от начальной формы импульса «(т) в (3), т.е. характеризует статистику сигнала на таком большом расстоянии т| , на котором в результате флуктуаций и дисперсионного расширения импульсов содержащаяся в них информация потеряна.
Таким образом, для расчетов распределений вероятностей оптических сигналов в нелинейных режимах, используемых для передачи информации (в частности, солитонном режиме) необходимы формулы типа (17), характеризующие неравновесные состояния.
Рассмотренный метод обеспечивает определение в явном виде 2Я-мерной плотности вероятности отсчетов флуктуирующего сигнала в любой точке оптического канала по заданному распределению на входе и поэтому при достаточно большом N применим для анализа как медленных, так и быстрых флуктуаций при любой форме импульса. Это позволяет записать в общем виде отношение правдоподобия и синтезировать оптимальные алгоритмы обнаружения и различения сигналов [4, 5].
Непосредственный численный расчет плотности вероятности по формуле (17) требует решения эволюционного уравнения (5), поэтому его целесообразнно осуществлять на ЭВМ рекуррентно, в соответствии с последовательной процедурой решения указанного уравнения (например, методом расщепления).
Высокие показатели качества нелинейных оптических систем передачи (малая вероятность ошибки, большие скорость и дальность) достижимы только при достаточно высокой степени когерентности излучения, когда приняты меры к подавлению быстрых флуктуаций и интервал когерентности превышает длительность импульса [4, 5]. При этом условии можно считать, что флуктуируют только параметры импульсов (например, амплитуды, скорости и фазы солитонов, как это принято в [6-9]), а их форма остается детерминированной.
Для анализа флуктуаций параметров описанный выше подход является неоправданно сложным, так как моделирование эволюции 2^-мерной плотности и последую !ци й расчет по ней распределений параметров на ЭВМ требуют очень больших затрат памяти и времени. В таких задачах более эффективен рассматриваемый ниже подход.
-
5. Анализ флуктуаций параметров с использованием автомодельных приближений
Уравнения эволюции параметров импульса в замкнутой форме могут быть выведены из НУШ (1) или (5); если принять допущение о сохранении формы импульса в процессе его распространения в среде передачи. Такое допущение справедливо для импульса гауссовской формы в линейном режиме и импульса секанс-гиперболической формы с определенными начальными параметрами в нелинейном односолитонном режиме. В остальных случаях указанные автомодельные решения можно рассматривать как естественные приближения к точному решению НУШ. Автомодельное решение НУШ вида (5) гауссовской формы получено в [14] и определяется выражением
Ч/Дпл^Ж^ехр'
1а^
+/2>(т|)т2
где Л(л), a(-q), Ь(т|) - параметры импульса (комплексная амплитуда, полуширина и коэффициент линейной частотной модуляции - ЛЧМ), изменяющиеся вдоль волокна.
Аналогичное решение в форме секанс-гиперболических импульсов (солитонов), выведенное вариационным методом в [15] для М мод, при Л/=1 можно представить в виде
^(Ч,^) = ^(Л) secA
т
Хп).
ехр[/Л(т1)т2] .
Как показано в [15], эволюция параметров моделей (21) и (22) описывается одинаковыми по виду уравнениями, отличающимися только числовыми коэффициентами И и ^ :
da
— = 4aab ;
^ х(23)
db Ц2Мт1) '
— = al—-44 I—
Для импульсов секанс-гиперболической формы ц^/л2 , ^-З/л2 ,_а для импульсов гауссовской формы с тем же значением Q получается ^=1, |^=1/2V2; если же фиксирована энергия импульса, то ц2=л/8^2. Уравнения эволюции параметров (23), как и исходное НУШ (5), могут быть представлены в гамильтоновой форме:
др = _8Н_. ^_ = ^L
(24)
5т| dq ’ дт| др где в качестве фазовых координат выбраны р = b, q = а2, (25) а гамильтониан определяется выражением г Hta 2|л2к^ Щр^) = 4ар q*--—1=- q Соответствующее уравнение Лиувилля для плотности вероятности w(p,q) имеет вид dw dw pta ц2к£ dw
--+ 8ap<7--4^--^+-^- = 0. (27)
dy dq ( q q^qjdp
Решив его методом характеристик, переходя от
q
к более удобному для анализа и измерений параметру - интенсивности
I—Q/^
и объединяя оба параметра в вектор
Z=4J,b\
можно представить связь распределения вероятностей w(Z,r|) на произвольном расстоянии т| с начальным распределением wo(2)=w(ZA0) в виде
w(Z,t))
= exp'
12aJ»©d(yE"«[^"'(2)] где Д2) - нелинейное отображение в двумерном пространстве параметров, определяемое уравнениями (23) с учетом указанной подстановки, Pf^Z) - i-ая ветвь обратного отображения. В отличие от 2^мерного распределения (17), двумерная плотность, определяемая (28), может быть сравнительно просто рассчитана на ЭВМ. Процедуре расчета целесообразно придать рекуррентный характер, соответствующий выбранному алгоритму решения уравнений эволюции Параметров (23). При этом плотность вероятности вектора отсчетов параметров ^=[/(ЛДт]), ^Дт])] в каждой последующей точке определяется по плотности в предшествующей точке согласно формуле (i+QAt) (?J = exp 12a J »©© k^‘(z,.,)] . *Дч где D(Z^ - отображение ^ в ^+1 , определяемое формулами Рунге-Кутта или другими аналогичными разностными соотношениями; £=0,1,2,...
6. Результаты моделирования и выводы
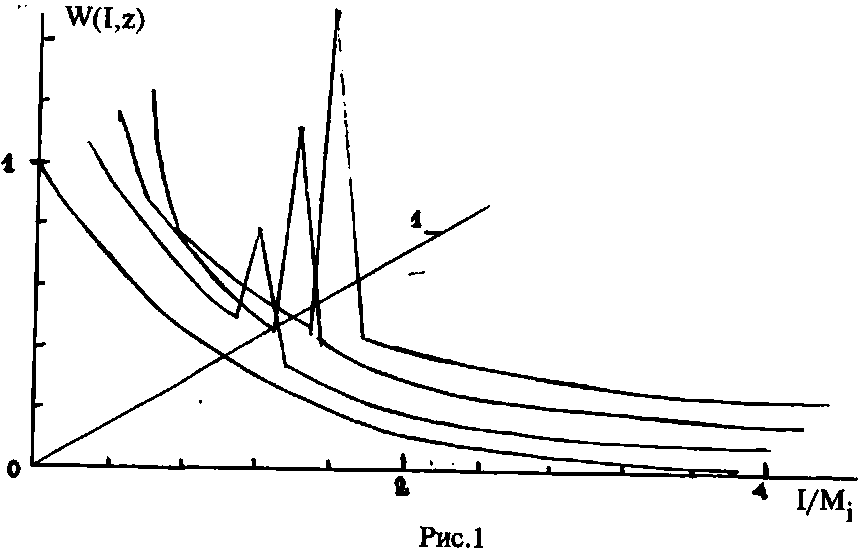
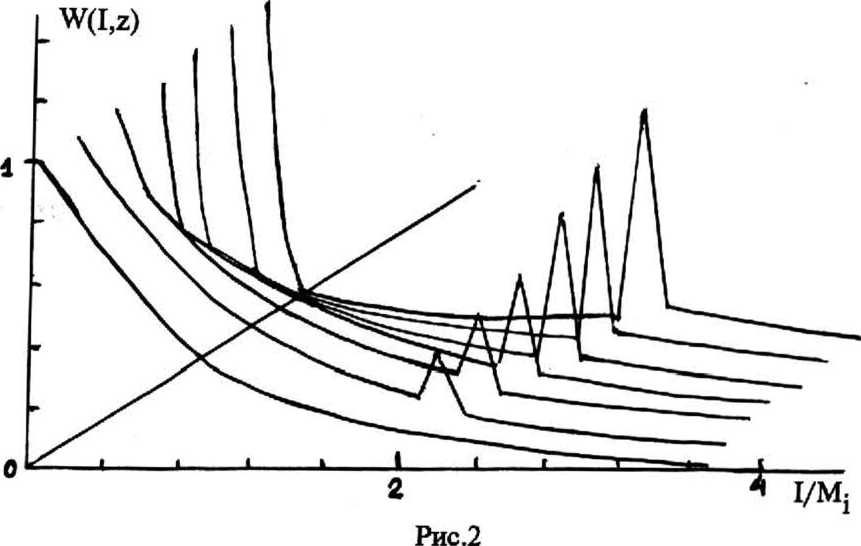
Для рассмотренных методов анализа распределений вероятностей были разработаны соответствующие алгоритмы моделирования на ЭВМ. На рис.1 и 2 в качестве примеров показаны полученные диаграммы эволюции плотностей вероятностей w(J,q) пиковой интенсивности импульсов секанс-Тийерболической формы для двух значений параметра нелинейности: к=2 и к=4 соответственно. Начальное распределение интенсивности принято экспоненциальным, что соответствует гауссовской модели флуктуаций квадратурных компонент, а для коэффициента ЛЧМ - равномерн
ым
, при постоянной энергии всех реализаций импульса. Значения интенсивности
I
на диаграммах нормированы на математическое олДдание
mv
Из диаграмм видно, что с увеличением т| экспоненциальное распределение быстро деформируется: образуется пик вблизи нуля, отражающий быстрое снижение пиковой интенсивности тех реализаций импульса, у которых ее начальное значение велико (а Длительность соответственно мала), вследствие дисперсии. В то же время реализации с малой начальной интенсивностью (и большой длительностью) сжимаются за счет нелинейного самовоздействия и их интенсивность растет. В результате действия этих факторов в плотности вероятности появляются дополнительные пики, соответствующие областям локальной самостабилизации импульсов. Значения интенсивности, при которых они образуются, тем выше, чем больше параметр нелинейности к. При к—0, т.е. в линейном режиме, вторичные пики, естественно, отсутствуют. Аналогичные зависимости наблюдаются и для импульсов гауссовской формы. Отмеченные закономерности подтверждаются результатами прямого статистического моделирования ПУТИ, которое было выполнено с целью их проверки. В частности, те же пики интенсивности обнаруживаются и на гистограммах распределений. Непосредственно из полученных диаграмм видно, что в рассматриваемых условиях интенсивность импульса в нелинейной диспергирующей среде флуктуирует по вероятностному закону, явно отличающемуся от экспоненциального, т.е. статистика Флуктуаций существенно отличается от гауссовской. Проверка соответствия распределений квадратурных компонент гауссовскому закону по критерию хи-квадрат Дает следующие результаты: для флуктуаций на входе получено х -7,74, на выходе, при Л~0,5 и к=4 х2=615. При этом уровню значимости а=0,1 соответствует х «24,1. Это означает, что воспроизводимая при моделировании статистика входного воздействия вполне удовлетворительно описывалась гауссовским законом, а на выходе нелинейного канала явно ему не соответствовала. Аналогичное моделирование для случая, когда нет ограничения, касающегося постоянства энергий всех реализаций, показывает, что деформация начального экспоненциального распределения при этом происходит значительно медленнее и без образования вторичных пиков. При тех же условиях на дальности т|=0,5 получено Х2=25,1, т.е. распределение флуктуаций, хотя и отличается от гауссовского, но не столь значительно, как в первом случае. В целом можно сделать вывод, что часто принимаемое допущение о близости статистики флуктуаций импульсных сигналов в нелинейно-дисперсионных оптических каналах к гауссовской неприемлемо в тех случаях, когда наложены ограничения на энергетические параметры сигналов. В остальных случаях расхождение с гауссовским законом хотя и наблюдается, но не столь значительно и на практике им можно пренебречь, особенно при малых значениях к. Рассмотренные методы расчета распределений вероятностей использованы при анализе помехоустойчивости, дальности, скорости передачи и других характеристик солитонных систем оптической связи и позволяют уточнить приведенные в [4, 5] их оценки.