Метод гармонического элемента в моделировании стационарных динамических процессов

Распространенность производств и технологических процессов, сопровождающихся высокой виброактивностью оборудования заставляет уделять повышенное внимание вопросам безопасности конструкций и рабочих мест. Особенно остро эти вопросы стоят на обогатительных и других производствах, специфика технологии которых требует размещения виброактивного оборудования на верхних этажах, что исключает возможность использования технологических фундаментов и приводит к непосредственной передаче динамических нагрузок на несущие конструкции перекрытий.

Перекрытия промышленных зданий представляет собой сложную, нерегулярную по расположению, геометрическим параметрам и узловым соединениям систему балок и плоских элементов - пластин. Виброактивность таких конструкций, наиболее интенсивно проявляется вертикальными составляющими колебаний, обусловленными режимами работы технологического оборудования. В примерах можно назвать горно-обогатительные производства, предприятия энергетики, угольной, деревоперерабатывающей промышленности, судовые транспортные системы и пр., где устанавливаются грохоты, вентиляторы, электродвигатели, электрогенераторы, компрессоры и другое виброактивное оборудование.

При оценке влияния виброактивного оборудования на состояние конструкций промышленных зданий и сооружений возникает необходимость моделирования процессов их динамического взаимодействия. Наиболее распространенные методы описания таких процессов основаны на дискретизации инерционных и жесткостных параметров элементов строительных конструкций (метод конечных элементов, метод граничных элементов, метод конечных разностей и т. д.).

Однако оценка погрешностей дискретизации динамических моделей с нерегулярными границами областей в большинстве случаев крайне затруднена. В этих условиях актуальны задачи построения дискретно-континуальных динамических моделей конструкций, подвер- женных гармоническим воздействиям. Такие модели не имеют погрешностей связанных с дискретизацией инерционных параметров.

Прямое формализованное описание динамики таких систем приводит к необходимости определения совместного решения совокупности уравнений в частных производных и обыкновенных дифференциальных уравнений. Трудность решения задачи в такой постановке усугубляется нерегулярностью границ областей и разнородностью граничных условий элементов конструкций.

Для расчета на стационарные гармонические воздействия конструкций, представленных совокупностью бесконечномерных балочных элементов, известен метод динамических податливостей, основанный на формировании уравнений динамического равновесия в соединительных узлах элементов по направлениям возможных перемещений узлов.

На основе развития методов динамической податливости разработаны дискретноконтинуальные модели, включающие бесконечномерные изгибаемые элементы (балки), материальные точки, твердые тела и пружины [2]. Создан программный комплекс, реализующий метод расчета систем, включающих произвольные комбинации таких элементов на стационарные гармонические воздействия [2].

Моделирование виброактивных систем, основанное на развитии метода динамической податливости позволяет использовать в качестве инерционных величин рассматриваемых систем как распределенные, так и сосредоточенные параметры. При этом сохраняются все свойства метода конечных элементов, позволяющего осуществлять решение при разнообразных граничных условиях и нерегулярности распределения физических и геометрических параметров. Сохранение свойств и некоторая аналогичность построения решений позволяет говорить о конечных элементах, но в отличие от классических вариантов специализированных для решения задач динамики и содержащих в качестве параметров частоту воздействия и распределенную массу. С учетом указанных особенностей такие элементы названы гармоническими элементами (ГЭ) . Осуществимая при этом узловая сшивка решений уравнений динамического состояния конечных элементов, полученных в виде амплитуд гармонических реакций в налагаемых связях, допускает аналитическое (функциональное) представление колебательных форм. Последнее обстоятельство значительно упрощает процедуры анализа и обобщения результатов решения и позволяет осуществлять нетрадиционные способы виброизоляции, основанные на формировании колебательных форм с заранее заданными свойствами. Метод, использующий свойства колебательных узлов в вынужденных формах колебаний упруго изгибаемых элементов, проиллюстрирован [2] на примере разработки системы виброизоляции промышленных грохотов, расположенных на деформируемых основаниях, - конструкциях.

С целью определения функций колебательных форм и построения матрицы динамических жесткостей рассмотрим вынужденные изгибные моногармонические колебания с частотой to балки с равномерно распределенной погонной массой р , длиной a, изгибной жесткостью EJ , при загружении ее постоянной продольной силой N . Для определенности рассмотрим расчетную схему с узловыми закреплениями, обеспеченными линейными и узловыми связями с номерами 1,2,3 (рис.1, в ).

Колебания балки осуществляется под воздействием сосредоточенных гармонических сил и моментов, приложенных в некоторых точках (узлах) балки. При отсутствии межузлового динамического воздействия уравнение динамического равновесия элементарного участка балки в пролёте между узлами описывается уравнением (1).

p V xx + EJV xxxx - NV xx = 0.                           (1)

При заданной частоте внешнего воздействия to колебательные формы балки однозначно определяются вектором амплитуд узловых гармонических перемещений

Y = (Y (°)- Y.lx =0- Y (1 )• U=a - (2) в котором компоненты расположены по порядку нумерации соответствующих связей. Вектор Y sin го определяет краевые условия для уравнения (1). Представим решение уравнения колебания балки в разложении по вынужденным колебательным формам от единичных гармонических перемещений (с единичными амплитудами) связей, обеспечивающих закрепления узлов. Единичное гармоническое перемещение каждой связи с номером i по своему направлению вызывает реакции во всех наложенных связях. Упорядоченные по номерам связей значения этих реакций образуют некоторый вектор Ri амплитуд гармониче ских реакций в связях. Поочерёдное гармоническое перемещение связей формирует матрицу динамических реакций R = {R1, R2, R3}.

Положительным считается реактивный момент. направленный по часовой стрелке и сила. действующая в положительном направлении оси Y (рис.2).

Расчетная схема рассматриваемого примера содержит три связи. В общем случае, количество связей задачи плоских изгибных колебаний может быть равным от двух до четырех.

Для определения коэффициентов матрицы R и функции амплитуд Y ( x ) вынужденных колебаний балки подставим искомое решение вида V ( x ) = Y ( x ) sin( ro t )

Y

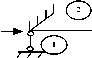
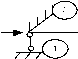
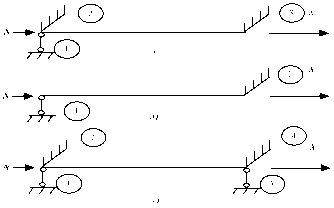
Рис. 1. Расчетные схемы балок с различными вариантами закреплений,1,2,3,4 – номера связей в уравнении (1).

Сократив полученное уравнение на sin( ro t ), получаем обыкновенное дифференциальное

уравнение:

⁽ IV ) ( x ) - NY ^{( )(} x ) - Y ( x ) ^-^ = EJ          EJ

Характеристическое уравнение для (3) имеет вид :

Ц

N ₂ го ² р

— ц--

EJ EJ

= 0.

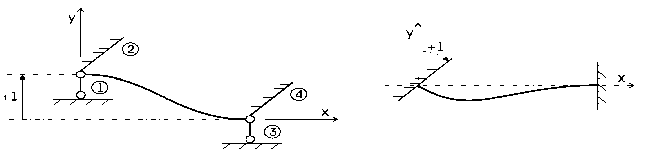
Рис . 2 Правило знаков реакций в связях

Определив

N       N ²     го ² р

-------±--1--

2 EJ 4EEJ )2 EJ ’ имеем

^i = q, где

^ 2 = - q ,

ц ₃ — is , и 4 — - is ,

q =^

N + 2 EJ }

N2     to 2 p 4 ( EJ ) 2 ' EJ

s —

N

\ 2 EJ

N

N 4 ( EJ ) ²

to2 p

EJ

Общее решение  Y(x) уравнения (3) может быть представлено в виде линейной ком- бинации

Y ( x ) = H (x ) C

четырех линейно независимых частных решений, образующих базисную вектор функцию H (x) = (eqx, e - qx ,sin( sx ),cos( sx)), где C является вектором коэффициентов линейной комбинации (4)

Краевые условия для решения уравнения (3) могут быть заданы в виде вектора (2) амплитуд перемещений по направлениям связей.

Для заданной схемы Y_xx| x = a = 0. При определении Y ( x ) коэффициенты линейных комбинаций фундаментального решения определяются в виде матрицы C путем поочередного задания единичных амплитуд перемещений по направлениям связей.

Векторы амплитуд единичных перемещений, упорядоченные по номерам связей образуют матрицу L. Матрицы C и L имеют вид:

	(с c ii	c 12	c 13 1		f 1	0	0 1
C —	c 21	c 22	c 23	L —	0	1	0
	c 31	c 32	c 33	'	0	0	1
	< c 41	c 42	c 43 у		I 0	0	0 J
Элементы матрицы C определяются из решения систем уравнений:

AC — L, где A - матрица, образованная из базисной вектор функции H(x) следующим образом:

f H(0) J

H x ^{( x )l} -x = 0 H^(l ) ( H,(x )L„J xx x a

Матрица амплитуд реакций в связях при попеременных единичных гармонических перемещениях связей в порядке их нумерации (матрица гармонических реакций) определяется в виде.

R = — EJC ^T H , где H = ( H^ ( x ) | x = ₀, H Xx ( x ) | x = 0 , HL ( x ) | _x = _a ) .

Вектор столбец Y амплитуд узловых перемещений, соответствующий вектору F амплитуд гармонических воздействий по направлениям связей с частотой ю определяется из решения системы уравнений

RY = F,   или  — EjA1 L) H=F.

Функция амплитуд перемещений оси балки (функция формы вынужденных колебаний) при заданной узловой форме F силового гармонического воздействия имеет вид

Y(x)=YT CT HT(x).

Наряду с балками в строительных конструкциях используются также плоские изгибаемые элементы (чаще всего в виде межэтажных перекрытий или рабочих площадок). Соответственно, представляет интерес включение в математические модели бесконечномерных изгибаемых гармонических элементов в виде тонких пластин. Такие элементы, так же как и балочные ГаЭ, обладая свойствами гибкой аппроксимации сложных границ областей и разнородных граничных условий, могли бы включаться в ранее разработанные дискретноконтинуальные модели ( ДКМ ). В отличие от балочного элемента в этом случае для большинства вариантов граничных условий не представляется возможным получить точные аналитические выражения решений.

Для этих целей приходиться использовать приёмы аппроксимации, схожие с конечноэлементными. Однако в отличие от классических конечноэлементных моделей при таком подходе удается избежать процедур дискретизации инерционных параметров пластины.

Покажем, что принцип динамической податливости в сочетании с методом гармонического сканирования связей, используемый для построения балочного гармонического элемента, может быть успешно применен и в этом случае.

Рассмотрим вынужденные изгибные колебания тонкой пластины. Дифференциальное уравнение поперечных колебаний пластины имеет вид:

д ⁴W _ д ⁴ W   д ⁴ W mh д ² W _А

—г + 2—-—х + —г +--у = 0, дx4     дx2cy2   ду4    D дt2

Так же как и в балочном элементе рассмотрим так называемые стоячие волны, получаемые при условии разделения переменных времени и пространства. Для этого представим функцию W ( x , у , t ) в виде:

W ( x , у , t ) = sin( tot ) g ( x , у ) .

Получаем

D ■ / л/д⁴ g      д⁴ g    д ⁴ g       ₂ .

— sin(tot)(—T + 2  2. 2 + ^4) = gto Sin(tot)• mh       дx     дx ду   ду

При sin( tot ) * 0

d 4s     d4s    d4s     ,

D(Y-g + 2 д g x + Y-g.) = to2 mhg.

д x⁴      д x ² д у ² д у⁴

Исключая параметр времени переходим к решению задачи стационарных колебаний, позволяющей пользоваться параметрами пространства в виде амплитуд перемещений и динамических реакций в связях. Прямое использование классических приемов конечноэле- ментного построения оказывается невозможным в силу того, что полученное уравнение (5) имеет в правой части неизвестную функцию to2mhg(x, у), выражающую распреде ленную инерционную нагрузку при достижении точек поверхности пластины амплитудных значений, тогда как при построении конечных элементов (КЭ) она известна и выражена зависимостью q(x, у), определяющей заданную поверхностную распределенную нагрузку. Уравнение деформированного состояния элементарного участка пластины в этом случае имеет вид:

д4 W 2 д4 W   д4 W) = дx4     дx2 ду2   ду4    ^

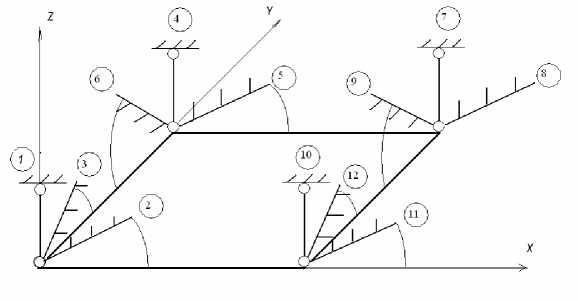
Рис . 3 Расчетная схема прямоугольного гармонического элемента

Для построения ГаЭ прямоугольной пластины рассмотрим достаточно распространенный в практике конечноэлементных разработок вариант четырехузлового элемента с узлами, расположенными в вершинах углов некоторой конечной прямоугольной области тонкой пластины. Используем принцип сканирования связей. Для этого наложим на возможные перемещения узлов связи, обеспечивающие кинематическую узловую неподвижность изгибаемого пластинчатого элемента (рис. 3).

В каждом узле необходимы три связи; одна линейная - по направлению оси Z и две угловых - в плоскостях ZoX и ZoY . Таким образом, степень кинематической подвижности элемента, которая определяет размерность параметрического пространства функции, интерполирующей поверхность перемещений g ( x , у ) , равна двенадцати.

Для построения гармонического элемента тонких прямоугольных пластин с жестким закреплением сформируем интерполирующие полиномы для базиса граничных условий, определенного возможными вариантами поочередных единичных перемещений узловых связей.

Для варианта возбуждения первой связи имеем:

^gx у) «Д ( x у) • A,                               (6)

2        2   3   2       2   3   3       2

где         Л ( x , у ) = (1, x , у , x , xy , у , x , x у , xy , у , x у, xy ) ,

A = (a 1 , a 2 , a ₃, a ₄, a ₅, a ₆, a 7 , a 8 , a 9 , a ₁₀, a^, a 1 ₂) .

(Индекс вектора коэффициентов определяется номером перемещаемой связи.)

Перемещая первую связь на единичную величину и фиксируя все остальные в нулевом положе -нии, определяем элементы вектора A ₁ путем решения системы уравнений:

V • A 1 = (1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0)¹ ,                             (7)

где V - матрица узловых условий поля перемещений.

Вычисляя значения	функции		Д ( x . у ) и	её производных	в узловых		точках	имеем развернутую
запись матрицы V : Г 1	0	0	00	000	0	0	0	0 "
0	- 1	0	00	000	0	0	0	0
0	0	- 1	00	000	0	0	0	0
1	0 с		00	с 2      0      0	0	с 3	0	0
0	- 1	0	0 - с	000	- с 2	0	0	- с 3
0	0	- 1	00	- 2 с    0     0	0	- 3 с 2	0	0
V= 1	bc		b 2    bc	c 2      b 3      b 2 c	bc 2	c 3	b 3 c	bc 3
0	- 1	0	- 2 b - c	0    - 3 b 2 - 2 bc	2 - c	0	- 3 b 2 c	- c 3
0	0	- 1	0 - b	- 2 c    0     - b2	- 2 bc - 3 c 2		- b 3	- 3 bc 2
1	b	0	b 2    0	0      b 3      0	0	0	0	0
0	- 1	0	- 2 b 0	0    - 3 b 2    0	0	0	0	0
_ 0	0	- 1	0 - b	0     0     - b 2	0	0	- b 3	0 _

Выполняя операцию обращения матрицы V имеем матрицу, столбцы которой являются коэффициентами полиномов g(x, y) интерполирующих функции перемещений поверхности пласти- ны при соответствующих вариантах задания граничных условий (вариантах перемещения узловых связей).

Например, при перемещении первой связи вектор коэффициентов полинома имеет вид:

A 1

1   0   0    - 3    - ¹    - 3    2      3       3      2

1  0  0   b2    bc    c2   b3   b2c   bc2   c3

- 2 -

1 T

.

b 3 c bc 3

Соответствующий интерполирующий полином представлен в виде:

^=1+ 3 A=1XV. 3 v2+2- 3+ A A+3- Л 2^2 2+- 3v-^x 3 g(x,y) 1 ' x ' xy ' y ' xx ' x y +' xx +' xy ' x y +' xy b2    bc c2    b3    b2c    bc2     c3     b3c    bc3

Имея равенство (8) можем для сформированных граничных условий определить аналитические выражения реакций в узловых связях.

^{% } =⁽% x    X y X xy ^{) T} .

Скомпонуем для этого вектор деформаций изгиба пластины в виде:

где ^{d 2} g .        в ² g . у - 2 ^d g — величины кривизны изгиба и скручивания пласти-

^X x ⁼ "1X2   ^х У ^{X xy}"    'у           ^г                "

ны.

Для определения вектора моментов { м } = ( M x м М_ХУ используем равенство:

{ M } = G { х } .                                       (9)

где для изотропного материала пластины

G = D • ц

ц

1 - ц

μ - коэффициент Пуассона,       Eh ³

Г 21 12 1 1 - ц ² I

Выполняя преобразование имеем выражение компонент вектора

{ M } через элементы

вектора A ₁ , - то есть через параметры интерполирующей функции.

Для определения реакций в связях воспользуемся условиями равновесия элементарного участка пластины:

дм  дMxy x +—3-2-- Q дx дy x

= 0

M + ^d My 5 x      8 y

—

Qy = ⁰

Подстановка найденных выражений компонент вектора

{ M } в (10) и (11) позволяет оп

ределить величины перерезывающих сил Q_x , Q y .

Условие равновесия выполняется на расчетной области почти всюду за исключением узловых точек, в которых величины Qx, Qy имеют разрыв в силу того, что в этих точках возникают реакции в линейных связях.

Для узловых точек справедливы условия равновесия в виде: Q x + Q y + ъ = о ^,

Величины линейных реакций r1 1, r4 1, r7 1, r10 1 определяются из равенств (11) при подстановке соответствующих координат узловых точек.

Выражения реакций в угловых связях определяются аналогичным образом из условий равнове- сия моментов в узловых точках.

M + M + r ., = 0 , x xy Xi ,1

M + M + r ., = 0 .                              (14)

y xy   yi ,1

То есть из (13) находим величину реакций в угловых связях 2,5,7,11 в плоскости ZoX , а из (14) -в связях 3,6,9,12 плоскости ZoY . Полученные величины r_n формируют первый столбец матрицы

R единичных реакций, определенных при помощи параметров вектора А, выраженных в свою очередь через: геометрические параметры h, b, с; механические параметры m, E, ц пласти ны; и частоту воздействия to.

Сформированные компоненты матрицы R не учитывают влияния распределенной инерционной нагрузки to2mhg(x, y), расположенной в правой части уравнения (5). Для ее учета воспользуемся теоремой о взаимности работ, согласно которой работа по преодолению внешних сил при перемещении связи равна работе, совершенной поверхностной нагрузкой при прогибах пластины.

Исходя из этого, при перемещении связи с номером i имеем:

rm 1 = Ц to 2 mhg2(x, y) 2    0   0       2

Таким образом, окончательно диагональный элемент формируется в виде суммы r" = ri + rm .                                   (16)

Формирование второго столбца матрицы R осуществляется аналогично при единичном перемещении второй связи. Система уравнений (7) при этом имеет вид:

V- А ₂ = (0,1,0,0,0,0,0,0,0,0,0,0) T .

Выполнение операций (7) - (15) с последовательной подстановкой столбцов матрицы A в выражение (6) формирует матрицу динамических жесткостей (амплитуд единичных динамических реакций) R , что позволяет аппроксимировать амплитудные состояния стационарных колебаний изгиба посредством узловых соотношений вида:

R - U = F , где U - вектор амплитуд обобщенных узловых перемещений, а F - вектор амплитуд узловых сил.

Таким образом, предложенный алгоритм реализации гармонического элемента обеспечивает устранение процедур дискретизации инерционных параметров пластины и связанных с ними погрешностей расчета. В алгоритме существование погрешностей обусловлено лишь наличием процедур аппроксимации жесткостных свойств пластины также неизбежных в дискретных методах. Параметры модели остаются распределенными, а исходное уравнение в частных производных не заменяется системой обыкновенных дифференциальных уравнений динамики, описывающих колебания материальных точек дискретизированных в узлах ансамбля элементов.

Моделирование стационарных колебательных процессов в системах, включающих балки и тонкие пластины, осуществляется на основе использования элементов с распределенным характером инерционных параметров.