Метод генерации случайного оптического поля с помощью разложения Карунена-Лоэва для имитации турбулентности атмосферы

Атмосферная оптическая связь даёт возможность передавать данные различного рода между объектами непосредственно в атмосфере без использования какого-либо оптического волокна, не занимая частоты в радиоэфире [1–4]. Такая беспроводная технология широко используется для создания каналов связи между многоэтажными домами и бизнесцентрами на так называемых участках последней мили, для соединения узлов связи от оператора до базовых станций сетей сотовой связи при больших объёмах передаваемого цифрового трафика, а также для связи объектов, когда прокладка кабеля невозможна или её стоимость велика [5, 6]. Современные атмосферные оптические линии связи могут обеспечить передачу данных на расстояния до 4 км и скорость передачи до 10 Гбит/с.

Хорошо известно, что с ухудшением погоды и повышением турбулентности в существующих системах оптической связи экспоненциально уменьшаются скорость передачи и предельное расстояние [7–9]. Поэтому множество усилий направлено на поиск возможности преодоления негативного влияния турбулентности среды. На сегодняшний день предлагается несколько способов решения этой проблемы: применение лазерных пучков со специальной про- странственной структурой [10–13], а также одновременно массивов пучков [14, 15], векторных пучков с неоднородной поляризацией [16–19] и частично когерентных пучков [20, 21].

Для анализа способности тех или иных пучков сохранять информационную стабильность при воздействии случайных флуктуаций оптической среды используется численное моделирование с имитаторами турбулентности, такими как диффузоры, рассеивающие экраны и ячейки турбулентности [22, 23].

При анализе и компенсации атмосферных искажений частот используется разложение Карунена–Лоэва (КЛ) [24, 25], обеспечивающее некоррелированность коэффициентов разложения [26, 27]. При этом оптимальные свойства функций КЛ очень близки к свойствам вытянутых сфероидальных волновых функций [28, 29]. Оба типа функций в общем случае не являются аналитическими, поэтому требуют решения задачи на собственные значения [30]. Однако для некоторых типов корреляционного оператора собственные функции имеют аналитический вид, в частности, для Гауссова распределения [31] и экспоненциальнокосинусного распределения [32].

В данной работе рассмотрен метод генерации случайного оптического поля (имитатора турбулентности) с помощью разложения КЛ для различных типов корреляционных операторов. Через сформированный имитатор случайной среды с Гауссовой корреляционной функцией были распространены однокольцевые пучки Лагерра–Гаусса с целью исследования способности оптических вихрей сохранять свою структуру.

exp [T ( x i , y i , u , v , z ) + T * ( x 2 , y 2 , u , v , z ) ]

= exp

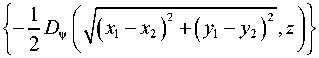
Для описания распространения лазерного пучка в среде со случайными искажениями используется расширенный принцип Гюйгенса–Френеля [33, 34]:

E ( u , v , z , t ) = —— exp(i kz ) x

2nz да да                                    / • 7

^xJ J E 0⁽ x , y ) ^x exp { 2- [ ( x ^- u )² + ( y ^{- v} )²p

-да -да

+ V ( x, y, u, v , z ) - i to t } d x d y ,

где D т (') - фазовая структурная функция, которая согласно теории турбулентности, развитой А.Н. Колмогоровым и А.М. Обуховым, зависит лишь от расстояния между двумя точками [37].

Используя метод плавных возмущений С.М. Рытова [38] для амплитудно-фазовых флуктуаций с учётом дифракционных эффектов [39], выражение (4) при квадратичной аппроксимации можно представить в виде [34]:

exp [V ( x _i , y _i , u , v , z ) + V * ( x ₂ , y ₂ , u , v , z ) ]^ ®

где E 0 ( x , y ) – поле во входной плоскости (при z =0); E ( u , v , z , t ) – поле на расстоянии z от входной плоскости; V ( x , y , u , v , z ) - случайная комплексная фаза, связанная с турбулентностью атмосферы.

Выражение (1) соответствует методу Рытова [9], а функция описывает случайные отклонения фазовой функции сферической волны, распространяющейся от исходной плоскости к выходной.

В связи с тем, что теоретические и экспериментальные параметры турбулентных сред рассматриваются в статистическом аспекте, расширенный принцип Гюйгенса–Френеля используется только для анализа усреднённых характеристик световых пучков, таких как средняя интенсивность [7, 9–11, 35].

Среднее распределение интенсивности пучка в выходной плоскости вычисляется через усреднение по ансамблю случайных реализаций неоднородности среды:

I ( u , v , z ) = ^ E ( u , v , z , t ) E * ( u , v , z , t )^, (2)

где знак «*» соответствует комплексному сопряжению.

Подставляя выражение (1) в (2), получим:

I ( u, v , z ) =

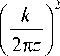
да да да да

J J J J E 0 ( X 1 , y i ) E 0 ( x 2 , y 2 ) x

-да -да -да -да

x /exp [V ( x i , y i , u , v , z ) + V * ( x 2 , y 2 , u , v , z ) ]\x

x exp { 2z [ ( x i - u ) 2 + ( y i - v ) 2

- ( x ₂ - u ) 2 + ( y ₂ - v ) 2 1 } d x 1 d y_i d x ₂ d y ₂ .

В интеграле (3) усреднение по случайным реализациям неоднородности турбулентной среды может описываться следующим образом [36]:

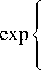
( x i - x 2 ) 2 + ( y i - y 2 ) 2 O o ( z )

где a ₀ ( z ) = (0,545 C „ ² k ² z) ^{- 3}5 - радиус корреляции (когерентности) волны, проходящей через турбулентную атмосферу на расстояние z , С_n ² – структурная постоянная среды.

Значения C_n ² могут меняться в зависимости от метеоусловий в пределах трёх и более порядков даже вблизи земной поверхности (высота около 2,5 м): от 10^–13 м^–2/3 для сильной турбулентности и до 10^–17 м^–2/3 для слабой. С увеличением высоты над землёй происходит уменьшение C_n ² по степенному закону [40]: при неустойчивом термическом состоянии атмосферы как С П ~ h - ^4/3, а при устойчивом более медленно С П ~ h ^{- 2/3} . Для коротких трасс визирования, когда можно пренебрегать зависимостью величины C_n ² от высоты h и не учитывать эффекты многократного молекулярно-аэрозольного рассеяния. Типичным средним значением считается С 2 = i0 ^{- i5} м ²³.

Как следует из приведенных выше рассуждений, для исследования влияния случайных флуктуаций оптической среды на некоторое поле E 0 ( x , y ) можно воспользоваться выражением (1) при условии генерации отдельных реализаций случайной функции V ( x , y , u , v , z ).

Для генерации реализаций случайного поля с заданными статистическими характеристиками (математическое ожидание и корреляционная функция) можно воспользоваться разложением КЛ [24].

Известно, что функции КЛ являются собственными для корреляционного оператора [24, 41–43]:

b n Ф n ( x 2 , y 2 ) =

= JJ q n ( x i , y i ) к ( x i , y i , x 2 , y 2 ) d x i d y i , n

где ф n ( x i , y i ) - собственные функции, b n - собственные числа, K ( x 1 , y 1 , x 2 , y 2 ) – ядро корреляционного оператора.

В нашей задаче ядро соответствует корреляционной функции (4) при фиксированном параметре z .

Для некоторых типов корреляционного оператора собственные функции КЛ имеют аналитический вид, в частности, для Гауссова распределения [31] и экспоненциально-косинусного распределения [32]. Однако в общем случае они не являются аналитическими и требуют решения задачи на собственные значения.

Рассмотрим несколько примеров численного расчёта функций КЛ для различных типов корреляционных функций, часто используемых для анализа случайных процессов [44], в частности:

K g ( X i ,y 1 ,x 2 , У 2 ) = exp

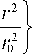
Kec (X1, У1, X 2, У 2 ) = exp I--1 cos | r |,(8)

I - o JI - )

Kb (Xi, y 1, X2, y2 ) = J01 r I,(9)

I - 0 )

Kl (X1,У1,x2,y2) = max|1 -r,0 |,(10)

___________ I где r = ^(X1 - х2 )2 + (y1 - y2 )2 , rо - масштабный параметр. В данном параграфе вместо радиуса корреляции, входящего в формулу (5), мы используем масштабный параметр корреляционной функции. Такой подход был использован в работе [45].

На рис. 1 показан вид четырёхмерных корреляционных матриц (7)–(10), развернутых в двумерную форму при х 1 , y 1 , х 2 , y 2 e [-1 мм, 1 мм], r 0 = 0,5 мм.

в)

а)

Рис. 1. Вид четырёхмерных корреляционных матриц, развёрнутых в двумерную форму: для Гауссова типа (7) (а), экспоненциально-косинусного типа (8) (б), Бесселева типа (9) (в) и линейного типа (10) (г)

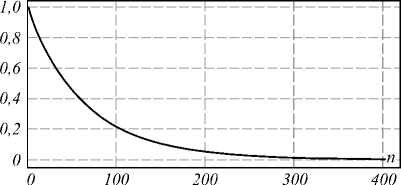
На рис. 2, 3 показаны рассчитанные для Гауссова типа корреляционной функции собственные числа bn и первые 12 собственных функций фn (х 1,y 1). При этом на рис. 2 показаны результаты для r0 =0,1 мм, а на рис. 3 – для r0 =0,5 мм. Как видно из сравнения картин собственных функций, масштабное изменение в корреляционной функции приводит также к уширению собственных функций. Но кроме этого, происходит существенное изменение результатов для собственных чисел – их значения резко убывают при уширении корреляционной функции. Таким образом, заметно сокращается число степеней свободы [46].

Очевидно, что чем шире корреляционная функция (в пределе стремится к постоянному значению), тем более коррелированными будут соседние значения случайного поля, т.е. оно фактически перестанет быть случайным. Таким образом, уменьшается число степеней свободы и число значащих собственных чисел и соответствующих им собственных функций.

И, наоборот, при сужении корреляционной функции (в пределе стремится к дельта-функции) соседние значения случайного поля становятся практически независимыми, приближаясь к белому шуму. Число степеней свободы растёт, ограничиваясь лишь числом отсчётов в матрице.

Стоит отметить, что с ростом размерности корреляционных матриц значительно возрастает вычислительная ресурсозатратность задачи на собственные значения. В частности, для размерности корреляционных матриц 100×100 отсчетов для решения задачи формируется матрица собственных векторов размерностью 10000×10000. Поэтому задача решалась с привлечением суперкомпьютера К-100 ИПМ им. М.В. Келдыша РАН.

□ЫИ$8И КИНИН®

Рис. 2. Расчёты для Гауссова типа корреляционной функции (7) при r 0 = 0,1 мм: собственные числа b n и первые 12 собственных функций ф п (х, y)

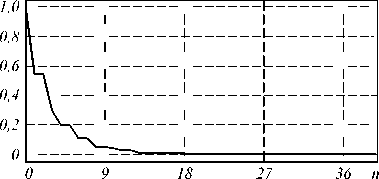
Заметим, что важен не только масштабный параметр о ₀, но и сложность функции. На рис. 4 показаны результаты расчета для экспоненциально-косинусного типа корреляционной функции (8) при r 0 =0,5 мм. Эти результаты можно сравнить с результатами для Гауссова типа корреляционной функции (7) с тем же параметром r 0 =0,5 мм, приведенными на рис. 3. Видно, что степеней свободы больше, хотя масштаб собственных функций тот же.

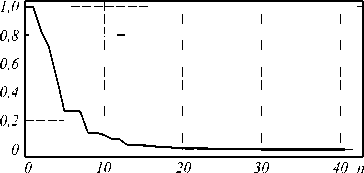
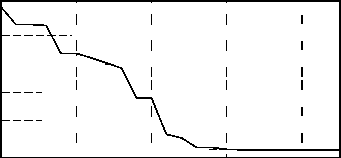
Очевидно, масштаб можно менять не только за счёт параметра r0 , но и за счёт интервала изменения координат. На рис. 5 показаны результаты расчёта для Бесселева типа корреляционной функции (10) при r0 = 0,5 мм и xi,уi,x2,у2 e [-3 мм, 3 мм].

□ HJL^*YH ^lir'ТЛЫ

^ft v л i *-*;*; ULe*A°

Рис. 4. Расчёты для экспоненциально-косинусного типа корреляционной функции (8) при r 0 = 0,5 мм: собственные числа b n и первые 18 собственных функций ф п (x, у)

^ ^^ ^^^ $^ t t ^^

Рис. 3. Расчёты для Гауссова типа корреляционной функции (7) при r0 = 0,5 мм: собственные числа bn и первые 12 собственных функций фп (x, у)

0         5          10        15        20 п

ЙВИЧИбЯННМУ ^9Qi10 88 88 89

Рис. 5. Расчёты для Бесселева типа корреляционной функции (9) при r 0 = 0,5 мм: собственные числа b n и первые 12 собственных функций ф п (x, y)

• 3 . Расчёт случайного имитатора
  
  для Гауссова корреляционного оператора

Для генерации реализаций случайного поля с заданными статистическими характеристиками (математическое ожидание и корреляционная функция) воспользуемся разложением КЛ [41–43]:

N и (x, у) = ц( x, у) + ^ an Фп (x, у),                 (11)

п = 0

где ц ( x , у ) - математическое ожидание случайного поля (принимаем его равным 0), N – количество рассматриваемых ортогональных функций разложения, Ф _п ( x , у ) - собственные функции корреляционного оператора (6). Коэффициенты a n суперпозиции (11) являются независимыми комплексными случайными величинами, имеющими нулевое математическое ожидание и дисперсию, равную собственному значению b n соответствующей собственной функции [41–43].

Рассмотрим формирование случайного поля с использованием выражения (11) для Гауссова распределения. Очевидно, Гауссов характер зависимости (5) является лишь частным случаем, однако это представление очень удобно для теоретического анализа. Кроме того, для Гауссова корреляционного оператора известен аналитический вид собственных функций и чисел [31]:

Ф i , q ( x , у ) = V i ( x ) V q ( x ), b l,q = d l d q ,

8R

V i ( x ) = -/==exp l -Uj£

хHl (л/sax), j a I a21

d/ =        1 + Vs I +—- l          21 l r0 V 2

х

- 1 - 1

,

где H l ( x ) - полином Эрмита, s = 1 +(2/ a r ₀)², a - коэффициент масштабирования.

При генерации случайного поля использовались следующие параметры: r 0 =0,3 мм, a = 16. Количество собственных функций, участвующих в разложении N =20.

На рис. 6 изображены амплитуда и фаза одномерного случайного поля. Сравнение теоретической и выборочной корреляционных функций для случайного поля приведено на рис. 7. Как видно, данный подход позволяет формировать случайные поля со статистическими характеристиками, очень близкими к заданным.

а)

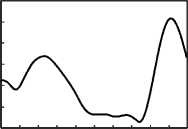
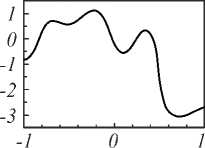
Рис. 6. Амплитуда (а) и фаза (б) одномерного случайного

комплексного поля

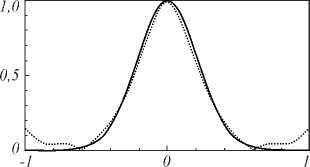
Рис. 7. Теоретическая (сплошная линия) и выборочная (пунктирная линия) корреляционные функции

На рис. 8 показана реализация случайного двумерного поля для r 0 =0,3 мм.

а)

Рис. 8. Амплитуда (а) и фаза (б) двумерного случайного комплексного поля

• 4 . Моделирование искажения вихревых мод имитатором случайной среды

В качестве входных пучков будем рассматривать моды Лагерра–Гаусса [47, 48]:

GL nm ( r , Ф ) =

m rrm

= exp -             L_n¹

n

I 2w2 Д w J r 2 )

— I exp ( im ф ) , w ² J

где L m ¹ ( ■ ) - обобщённые полиномы Лагерра [47], n , m – радиальный и угловой индексы, w – радиус перетяжки Гауссова пучка.

При моделировании искажения мод Лагерра–Гаусса (15) с использованием рассчитанного имитатора случайной среды были выбраны следующие параметры: X = 532 нм, w =0,2 мм, z =100 мм, радиальный индекс n =0, порядок оптического вихря m варьировался.

На рис. 9 представлены изображения вихревого пучка с m =3 до и после прохождения среды со случайными искажениями. Моделирование распространения выполнялось с использованием оператора распространения (1) для Гауссовой зависимости (5).

Оценка сохранения модовых свойств искаженного пучка выполнялась на основе разложения поля по угловым гармоникам, которое позволяет определить состояние орбитального углового момента [49, 50]:

2п R cp = J J E(r, ^’ z)exp(-iP^)r d^ dr,              (16)

где E ( r , ф , z ) - анализируемый пучок.

Результаты расчётов собраны в табл. 1.

Как видно из табл. 1, увеличение порядка оптического вихря m приводит к меньшей стабильности модовых свойств вихревых пучков к случайным оптиче- ским флуктуациям, что согласуется с ранее полученными экспериментальными результатами [14].

а)

б)

Рис. 9. Интенсивность и фаза оптического поля, соответствующего моде Лагерра–Гаусса (n, m) = (0,3) на входе (верхняя строка) и на расстоянии z = 100 мм (нижняя строка)

Табл. 1. Содержание оптических вихрей порядка p в пучке Лагерра–Гаусса с порядком вихря m после прохождения случайной среды

	m =0	m =1	m =2	m =3	m =4	m =5
p =0	0,9822	0,0085	0,0382	0,0024	0,009	0,074
p =1	0,0023	0,9493	0,0293	0,0523	0,0061	0,0123
p =2	0,0059	0,0042	0,8875	0,0667	0,0627	0,015
p =3	0,0038	0,0126	0,0064	0,805	0,1151	0,0733
p =4	0,0003	0,0067	0,0222	0,0094	0,6981	0,1617
p =5	0	0,0005	0,0085	0,0332	0,013	0,5743

Заключение

В работе рассмотрен метод генерации случайного оптического поля (имитатора турбулентности) с помощью разложения Карунена–Лоэва для различных типов корреляционных операторов. Через сформированный имитатор случайной среды с Гауссовой корреляционной функцией были распространены однокольцевые пучки Лагерра–Гаусса с целью исследования способности оптических вихрей сохранять свою структуру. Результаты моделирования показали качественное согласование с ранее полученными экспериментальными результатами.

Данная работа была выполнена при финансовой поддержке Российского фонда фундаментальных исследований (гранты №№ 18-37-00056 мол_а, 18-2920045 мк) в части расчета имитаторов случайных полей на основе разложения Карунена–Лоэва и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (согла- шение № 007-ГЗ/Ч3363/26) в части моделирования искажения мод Лагерра–Гаусса.

ГРНТИ: 29.31.15 .