МЕТОД ГЛАВНЫХ КОМПОНЕНТ КАК АЛЬТЕРНАТИВНЫЙ АЛГОРИТМ ОБРАБОТКИ ДАННЫХ ТЕРМОКАТАЛИТИЧЕСКИХ СЕНСОРОВ

В настоящее время ввиду увеличения числа промышленных объектов, в том числе потенциально опасных, широкое распространение получили исследования в области охраны окружающей среды, которые сориентированы на снижение возможных последствий той или иной деятельности. Исследования направлены на разработку эффективных методов контроля норм допустимых воздействий на безопасность жизнедеятельности человека и природных экосистем. Среди таких исследований особое место занимают исследования по созданию и применению систем мониторинга среды, окружающей человека. Одним из направлений данного вида мониторинга является разработка датчиков для анализа газового состава воздуха, которые не только определяют концентрацию того или иного целевого газа, но способны распознать этот газ в составе смеси. Это делает совершенствование методов газового анализа и их применение в быту и промышленности актуальной задачей.

Традиционные методы анализа состава воздушной среды основываются на статистических методах обработки информации, в частности на таких фундаментальных, как количественный и качественный анализы. В данном случае качественный анализ направлен на идентификацию различных газов, которые присутствуют в воздухе, а количественный анализ — на определение концентрации анализируемого типа газа.

Для анализа состава воздуха используют газовые сенсоры различных типов [1–3]. Их всех объединяет тот факт, что все они преобразуют концентрацию анализируемого газа в электрический (реже в другой) сигнал. Такие измерения являются относительно простыми и фактически не содержат какой-либо математической обработки, за исключением простейшего пересчета концентрации в ток или напряжение. Для выполнения данного пересчета сенсоры калибруются на целевой газ.

Такой подход ограничивает возможности всех видов газовых сенсоров, в частности требует точного знания типа газа в воздухе. Это связано с тем, что, как правило, газовые сенсоры не обладают селективностью, т.е. способны "чувствовать" разные газы, в том числе и одновременно. Проблема низкой селективности присутствует в самом подходе при традиционных измерениях, когда объем данных недостаточен.

В частности, для проведения измерений термокаталитический сенсор калибруется в двух точках: при нулевой и известной концентрациях газа. Таким образом, фактически измеряется конечная температура сенсора при известной концентрации, т.е. результатом является только одно измеренное значение температуры. Это не позволяет использовать данный метод для газовых смесей неизвестного состава, поскольку сенсор будет реагировать на все горючие газы в воздухе.

Решить проблему селективности можно двумя способами: доработкой самих сенсоров (например, за счет применения фильтров, пропускающих только целевой газ, катализаторов и т.д.) [4]

или разработкой математических методов обработки получаемых данных.

В условиях быстрого развития технической и технологической базы, а также цифровой экономики возрастает важность применения математических методов анализа данных большого размера. Особое место в исследованиях занимают мульти-сенсорные системы [5], которые состоят из набора сенсоров и системы распознавания. Во многих случаях количество сенсоров превышает 3, что увеличивает количество исследуемых образцов газа. Поэтому при анализе данных, полученных при работе с большим количеством сенсоров, следует выбрать наиболее удобный метод обработки данных, чаще всего используются метод главных компонент (МГК) [6–8] и линейно дискриминантный анализ (ЛДА) [7].

В работе [7] представлены результаты анализа МГК и ЛДА для откликов массивов сенсоров на диоксид азота, аммиак и хлор. Области локализации откликов на газы различны, что позволяет распознать, какой газ воздействует на систему. Таким образом, МГК хорошо распознает отклики сенсора на разные газы.

Исследования в работе [8] показали, что полученные количественные характеристики различий образцов целесообразно использовать для автоматической классификации методами многомерной статистики. Данный результат показывает принципиальную возможность использования МГК для разделения типов исследуемых газов.

Задачей данного исследования является оценка возможности применения МГК в качестве альтернативной методики обработки данных термокаталитических сенсоров, в частности для измерения концентрации метана в воздухе для сенсоров с разной рабочей температурой. Важность данных исследований связана с оптимизацией параметров и характеристик термокаталитических сенсоров, в частности чувствительности и селективности, а также с необходимостью изменения методик измерения для получения большего числа данных для последующей математической обработки и повышения селективности сенсоров.

МЕТОДИКА ЭКСПЕРИМЕНТА

При исследовании сложных химических систем можно выделить два подхода [6]:

– построение содержательных моделей в виде систем дифференциальных или интегро-дифференциальных уравнений и применение к ним специальных методов решения;

– анализ данных, основанный на многофакторном формальном моделировании.

Формальное моделирование часто эффективно в случаях, когда непонятно, как строить содержательную модель, либо ее построение требует чрезмерных вычислений.

В основе многофакторного анализа данных лежат проекционные методы. Эти методы позволяют выделить в больших массивах данных скрытые переменные и анализировать связи, существующие в изучаемой системе.

Важное место в методах анализа многомерных данных занимает МГК. Центральная концепция метода — понятие главной компоненты. Так называют специальный тип скрытой переменной, которая описывает максимальное разнообразие данных. Она не может быть объявлена явно и непосредственно измерена. В математическом смысле главная компонента — это линейная комбинация всех объясняющих признаков. При этом к первой главной компоненте относят максимум общей дисперсии объясняющих признаков, ко второй — максимум оставшейся дисперсии без учета влияния первой и т.д.

После использования МГК новая модель имеет существенно меньшее количество переменных, в силу чего такой подход может интерпретироваться как проекционный.

В качестве сенсоров были взяты промышленные термокаталитические сенсоры, которые серийно выпускаются фирмой "НТЦ ИГД" [9]. Сенсор состоит из рабочего и сравнительного элементов, которые находятся в одном корпусе (рис. 1).

Обычно для проведения измерений сенсор нагревается до рабочей температуры, при которой имеет место горение целевого газа. Рабочая температура сенсора может варьироваться в достаточно широком диапазоне и зависит от протекающего через сенсор тока. Так как горение происходит с выделением тепла, то температура сенсора изменяется. В свою очередь это приводит к изменению сопротивления сенсора, которое регистрируется измерительной схемой. Это одно измеренное значение и является откликом сенсора.

В данном исследовании проводилось изучение температурной зависимости отклика сенсора. Была применена методика измерения откликов сенсоров, описанная в работе [10], которая позволила получить экспериментальные зависимости отклика сенсоров от приложенного к мостовой схеме напряжения питания для метана при концентрации 0.47 и 2.5% об. Были исследованы три группы сенсоров с рабочей температурой 409, 444 и 478 ºС, которая определяется рабочим током 46, 50 и 54 мА соответственно. При постоянном рабочем напряжении (2.8 В в мостовой измерительной схеме [11]) разный рабочий ток достигается за счет разного начального сопротивления сенсора.

б

Рис. 1. Фотография термокаталитического сенсора.

а — внутренний вид сенсора (черный цилиндр — рабочий сенсор, белый цилиндр — элемент сравнения);

б — внешний вид корпуса сенсора

Табл. 1. Характеристика исследуемых групп сенсоров

Номер сенсора (образец)	Сопротивление при комнатной температуре (R o ), Ом	Рабочий ток, мА	Рабочая температура, °C
1	14.3	46	409
2	12.7	50	444
3	10.9	54	478

Далее при описании результатов будем оперировать номерами сенсора в соответствии с приведенной табл. 1.

Для исследования исходные данные, т.е. измеренные температурные зависимости отклика сенсора, были разделены на три набора значений:

– две концентрации применяемого газа при одном значении тока;

– одна концентрация применяемого газа при каждом значении тока;

– две концентрации применяемого газа при каждом значении тока.

Каждый набор обработан при помощи МГК, после чего наиболее оптимальный набор исследован в соответствии со следующей методикой.

Ввиду того, что метод чувствителен к значениям исходных данных с большим диапазоном [12], данные должны быть стандартизированы:

x, - x si = -—, σ где    si — стандартизированное значение;

x_i — исходное значение;

x — среднее арифметическое исходного значения;

σ — стандартное отклонение исходного значения.

Стандартизированные данные обрабатываются при помощи МГК. Главные компоненты имеют три показателя информативности: стандартное отклонение главной компоненты, доля объясненной дисперсии, кумулятивная доля объясненной дисперсии [13].

По этим показателям производится поиск оптимального представления данных, т.е. определение количества главных компонент, достаточных для объяснения исходных данных. Существуют три правила поиска: правило Кайзера (значимы те компоненты, собственное значение которых превосходит единицу), "тест осыпи" (оптимальное количество определяется как число, при достижении которого прирост объясненной дисперсии становится незначительным) и эмпирическое правило (количество главных компонент зависит от совокупного процента объясненной дисперсии, который должен быть не менее 80%).

После выбора количества главных компонент необходимо рассмотреть веса исходных данных, с какими они входят в полученные главные компоненты, и определить наиболее значительный. Это позволит узнать, какая переменная оказывает наибольшее влияние на главную компоненту.

Таким образом, исследование было проведено в следующей последовательности:

– стандартизация исходных данных;

– применение МГК к стандартизированным данным;

– определение трех показателей информативности главных компонент;

– поиск оптимального представления данных (количества главных компонент);

– определение переменной, оказывающей наибольшее влияние на выбранную главную компоненту.

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

На рис. 2 представлены S-образные зависимости отклика термокаталитического сенсора от подаваемого напряжения питания в установившейся атмосфере, содержащей метан.

Из полученных зависимостей видно, что для каждого образца концентрации 0.47% об. и 2.5% об. имеют практически одинаковый характер изменения (температура сенсора влияет на стадию начала каталитической реакции и стадию насыщения), что позволяет однозначно определить, какая концентрация метана в воздухе.

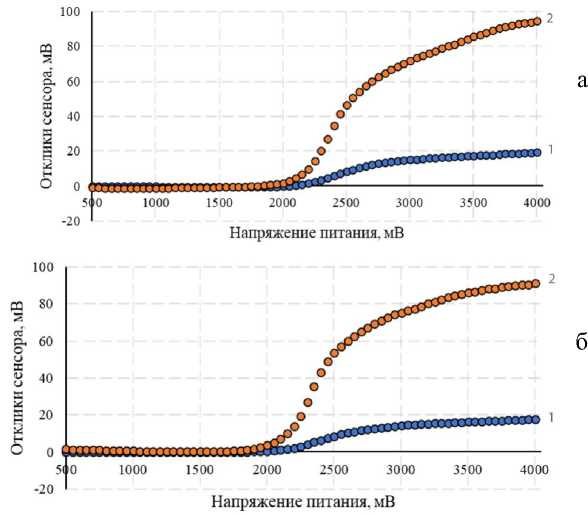
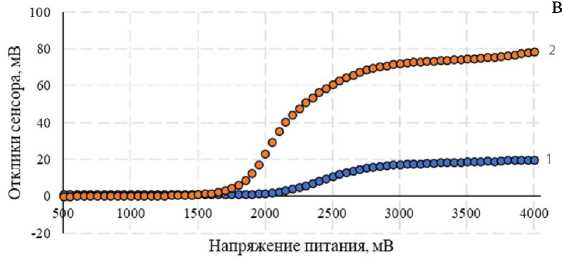
Рис. 2. Экспериментальная зависимость отклика сенсора от напряжения питания на концентрации метана 0.47% об. и 2.5% об. а — образец № 1, б — образец № 2, в — образец № 3

На рис. 2, в, отклик сенсора образца № 3 на концентрации 2.5% об. на 10 мВ меньше, чем у образцов № 1 и № 2.

На рис. 3 представлены экспериментальные зависимости отклика сенсора от напряжения питания при одной концентрации. Важно отметить, что при традиционном методе измерения при напряжении 2.8 В все сенсоры для каждой концентрации метана показывают близкое значение отклика.

Как видно из полученных зависимостей, отклик сенсора отсутствует до напряжения питания 2 В на образцах № 1 и № 2 и 1.6 В — на образце № 3. В то же время характер изменения отклика сенсора трех образцов схож между собой как при концентрации 0.47% об., так и при 2.5% об. Предполагается, что влияние рабочей температуры на отклик будет минимально, что позволит не учитывать в исследованиях рабочий ток сенсора для уверенного распознавания типа газа.

Исходя из приведенных экспериментальных зависимостей, при использовании одного сенсора графически распознать и проанализировать к он-центрацию газа возможно, но с увеличением количества сенсоров в системе возрастает объем получаемых данных, что усложняет процесс анализа. В частности, в данном исследовании рассматривается система, состоящая из 8 сенсоров. В таких системах важно организовать исходные данные и оценить, какие признаки имеют наибольшее влияние.

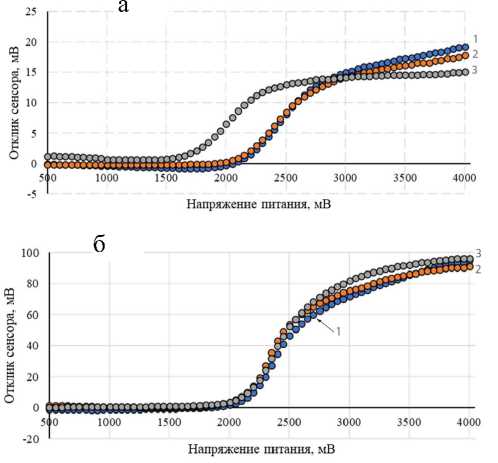
Рис. 3. Зависимость сенсорного отклика от напряжения питания для трех образцов (1 — образец № 1, 2 — № 2, 3 — № 3).

а — на концентрации метана 0.47% об.; б — на концентрации метана 2.5% об.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Обработка исходных данных реализована средствами языка python 3.9.5 с использованием библиотек numpy v1.20.3, pandas 1.2.4, sklearn 0.0, а также в среде программирования Rstudio 1.4.

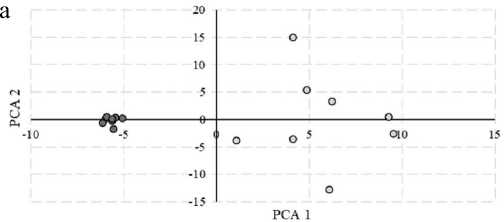
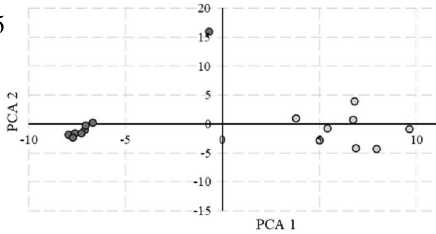
Рис. 4. Зависимость значений первой ГК (РСА 1) от второй ГК (РСА 2) на концентрациях метана 0.47% об. и 2.5% об.

а — для образца сенсора № 1; б — для образца № 2; в — для образца № 3

00.47% об.

02.5% об.

Результаты обработки набора значений двух концентраций при одном токе при помощи МГК приведены на рис. 4.

Как видно из полученных графиков, области распознавания двух концентраций возможно однозначно выделить. Области локализации распределены слева направо, т.е. вдоль первой ГК (на графике РСА 1). Рассмотрев веса каждой ГК, полученные в ходе обработки, можно отметить, что первая ГК связана с откликом сенсора при напряжении питания [2500, 2700] мВ, т.к. значения в данном диапазоне имеют наибольшее отклонение для двух концентраций, а вторая ГК — в диапазоне [1103, 1453] мВ.

Согласно рис. 4, разброс значений распределен вдоль второй ГК (на графике PCA 2). В табл. 2 представлены значения дисперсии исходных данных и второй ГК.

Табл. 2. Дисперсия исходных данных и ГК

Концентрация метана	Образец № 1		Образец № 2		Образец № 3
	Исходные данные	Вторая ГК	Исходные данные	Вторая ГК	Исходные данные	Вторая ГК
0.47% об.	0.093	0.491	0.571	37.381	0.208	23.961
2.5% об.	11.722	65.886	0.111	8.021	0.132	15.212

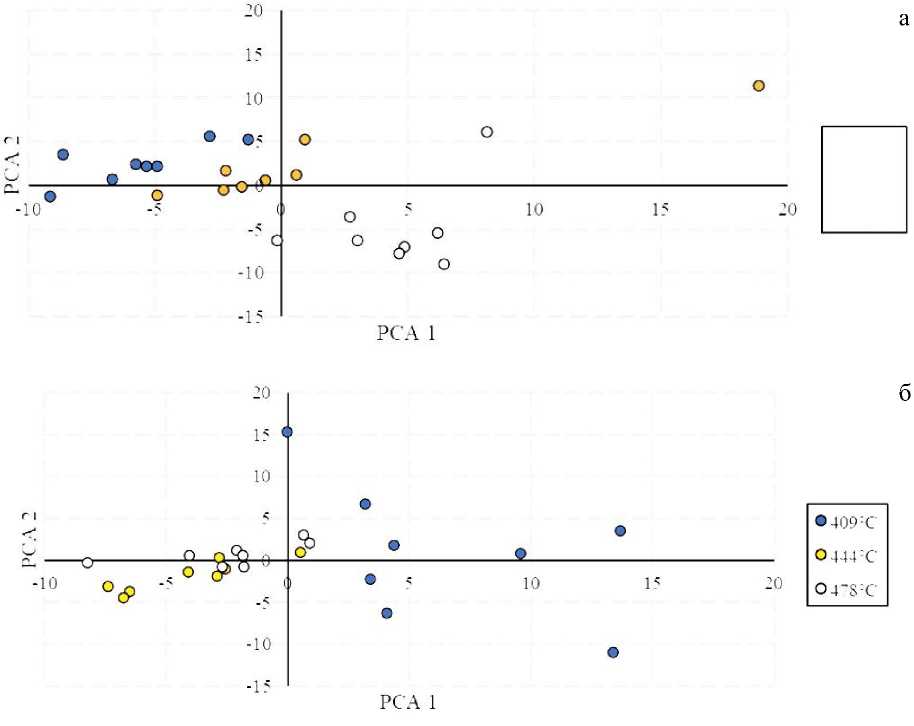
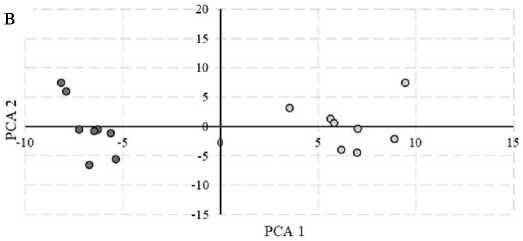
Рис. 5. Зависимость значений первой ГК (РСА 1) от второй ГК (РСА 2) для трех образцов сенсора. а — на концентрации метана 0.47% об.; б — на концентрации метана 2.5% об.

0-109	С
0 444	С
0478:	с

Полученный результат показывает, что разброс напрямую связан со значениями исходных данных. В образце № 2 на концентрации 0.47% об. присутствует единичный выброс, вследствие чего дисперсия сильно увеличена. Аналогично представлено в образце № 3.

В итоге, несмотря на разброс значений каждой из ГК, можно сделать вывод, что распознавание концентраций при одном токе возможно.

Результаты обработки набора значений одной концентрации при трех токах с помощью МГК приведены на рис. 5.

Из полученного графика видно, что области распознавания при одной концентрации, но разном значении тока выделить возможно, но они имеют пересечения. В данном случае возможен вариант использования таких данных для распознавания одной концентрации, но не для разделения на значения тока.

Результат обработки набора значений двух концентраций при трех токах при помощи МГК приведен на рис. 6.

Как видно из графика, рассчитанные данные при концентрации 0.47% об. образовали единую область распознавания. Аналогично можно выделить область для концентрации 2.5% об., хотя и имеется большой разброс между данными каждого сенсора при температуре 409 °С, отклонение в среднем составило ~5 мВ. Из этого можно сделать вывод, что при обработке исходных данных зависимость от тока потребления минимальна, следовательно, значения на одной концентрации при разных токах можно совмещать в один набор данных.

Рассмотрим информативность этого набора значений с применением трех правил поиска оптимального представления данных. Собственные значения главных компонент по правилу Кайзера (значимы те компоненты, собственное значение которых превосходит единицу) представлены в табл. 3.

• •    0.4”% об..409°С

02.5% об..409°С

• •    ОЛ^о об..444°С

С2.5% об..444°С

СО.47% об.. 478°С

О2.5%об..478°С

Рис. 6. Зависимость значений первой ГК (РСА 1) от второй ГК (РСА 2) на концентрациях метана 0.47% об. и 2.5% об.

Табл. 3. Собственные значения главных компонент

№ п/п	Номер главной компоненты	Собственное значение
1	ГК 1	38.55168
2	ГК 2	23.85346
3	ГК 3	7.008886
4	ГК 4	0.836804
5	ГК 5	0.566286

Табл. 4. Совокупный процент объясненной дисперсии

№ п/п     Номер главной компоненты	Совокупный процент объясненной дисперсии, %
1                ГК 1 2             ГК 2 3              ГК 3 4             ГК 4 5              ГК 5	54.3 87.9 97.776 98.954 99.752

Как видно из полученных данных, по правилу Кайзера можно утверждать, что для представления исходных данных достаточно трех главных компонент.

Значения совокупного процента объясненной дисперсии представлены в табл. 4.

По эмпирическому правилу, совокупный процент объясненной дисперсии должен быть не менее 80%. Исходя из данных табл. 4, для представ- ления исходных данных достаточно двух главных компонент для трех наборов данных.

По "тесту осыпи", оптимальное количество определяется как число, при достижении которого прирост Δ объясненной дисперсии становится незначительным. Зависимость доли Δ объясненной дисперсии от количества главных компонент представлена на рис. 7.

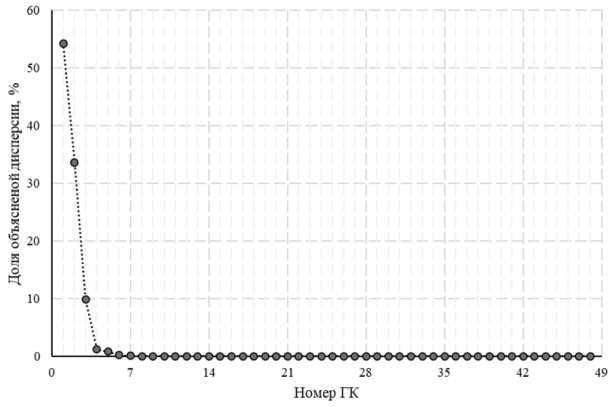
Рис. 7. Зависимость доли Δ объясненной дисперсии от количества главных компонент

Как видно из полученных зависимостей, прирост Δ объясненной дисперсии становится незначительным при достижении третьей главной компоненты, следовательно, можно предположить, что оптимальное количество главных компонент равно 3.

Полученные результаты по трем правилам показали, что для объяснения исходных данных в каждом из трех наборов оптимальное и необходимое количество главных компонент равняется 3.

ЗАКЛЮЧЕНИЕ

В работе было проведено исследование альтернативной методики обработки данных термокаталитических сенсоров на основе метода главных компонент для измерения концентрации метана в воздухе (0.47% об. и 2.5% об.) сенсорами с разной рабочей температурой (409, 444 и 478 ºС). Представленная методика исследования позволяет найти оптимальный набор исходных данных, определить количество главных компонент и оценить влияние данных на главные компоненты.

Показано, что при обработке исходных данных при помощи МГК влияние рабочей температуры минимально, что позволяет совмещать значения на одной концентрации в один набор данных. Методика позволяет однозначно различать отклики образцов разной концентрации метана без использования дополнительных операций подготовки данных.

Полученные результаты имеют важное значение для разработки и оптимизации методов анализа состава воздуха, в частности позволят перейти от пересчетов концентрации "внутри" сенсора к математической обработке получаемых с сенсора данных и на ее основе проводить распознавание поданого газа. Так как МГК относят к методам машинного обучения без учителя, то при объединении нескольких сенсоров в единый комплекс возможно создание системы распознавания типа газа с возможностью обучения на получаемых в процессе работы данных. Также остается актуальным вопрос о возможности применения МГК при анализе смеси, состоящей их двух и более типов газа.