Метод групповой адаптации с фиксацией смещений нейронов (АФСН) для прогнозирования показателей качества объемных извещателей

В работах [1, 2] было установлено, что для решения обратной задачи экспертизы наиболее предпочтительным с точки зрения минимума числа необходимых итераций является алгоритм Левенберга–Маркуардта (LM). Однако этот алгоритм является наилучшим и с точки зрения других показателей. Так, в работе [3, стр.75] приведена таблица сравнения эффективности двух градиентных алгоритмов и алгоритма LM при решении одной и той же задачи, и показано, что последний существенно превосходит градиентные алгоритмы по требуемому времени (соответственно — 57,7 с, 19,2 с, 1,8 с) и необходимому числу элементарных операций.

Однако реализация этого метода с помощью графического редактора GUI языка MATLAB имеет два серьезных недостатка: 1) неоднозначность решения, обусловленная случайным выбором начальных весов и смещений; 2) получение набора весов, противоречащих весам V_i исходной регрессионной модели.

Поясним второй недостаток, рассматривая уравнения линейной множественной регрессии [4, 5]:

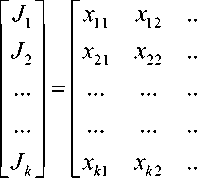
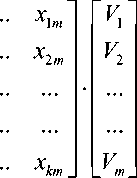
где V_i — коэффициенты регрессии (весовые коэффициенты).

В задачах экспертизы предполагается [6], что весовые коэффициенты неотрицательны и принимают значения из промежутка [0, 1]. Например, в работе [7] вектор весовых коэффициентов, определенный для экспертизы объемных извещателей, имел вид:

V = ( 0 , 649 0 , 122 0 , 229 1 , 000 ) T , (2) т.е. его элементы положительны и не превосходят величины 1,0.

При нейронном моделировании в той же статье нами был введен расширенный вектор весов и смещений для двухслойной сети:

1       1       1        1       1      22

Q = ( w_{i 1} , w_{i 2} , w_{i 3} , w _{i 4}, b ; w ₁ , b )^Т , где w_i^l_j — синаптические веса l -го нейрона ( l = 1,2), b^l — смещения l -го нейрона ( l = 1,2).

Даже для случая одного нейрона в скрытом слое вектор Q был получен в виде [7]:

Q = (1,426 -0,614 -1,723 2,307 0,224 0,297 -0,880) ^T , (3)

что совершенно отличается от (2). Как видим, нарушено требование неотрицательности весовых коэффициентов и требование V <  1 .

Полученные результаты являются следствием известной [5] проблемы переобучения нейронной сети. Действительно, для калибровки регрессионной модели требуется найти 4-мерный вектор весовых коэффициентов { V } , а решение задачи мы ищем в 7-мерном пространстве весов и смещений.

Таким образом, при нейронном моделировании осуществляется калибровка одно- или двухслойной нейронной модели, а не модели линейной множественной регрессии. Иначе говоря, при использовании описанного выше подхода обучения ( train ) нейронной сети с применением средства nntool и графического редактора GUI калибровка линейной регрессионной модели невозможна . Это является крайне нежелательным фактором, поскольку означает разрыв методологического единства решения прямой и обратной задач экспертизы.

Целью данной статьи является разработка метода адаптации нейронной сети с фиксацией смещений (АФСН), обеспечивающего прогнозирование показателя качества нового объекта экспертизы с обеспечением возможности восстановления регрессионной модели.

Сравним различные методы прогнозирования обобщенного показателя качества нового объекта экспертизы (рисунок 1). Последовательно, слева направо, представлены два метода нейронного моделирования (обучение с учителем и адаптация) и метод решения тестовой задачи.

Во всех трех случаях исходной информацией является множество референтных данных объектов экспертизы X и множество показателей качества известного набора образцов J .

Как было отмечено выше, метод обучения на основе средства nntool и графического редактора GUI не дает возможности калибровки регрессионной модели. Однако, если пропустить этот этап, прогнозирование показателя все же возможно с помощью процедуры sim, причем с достаточно высокой точностью.

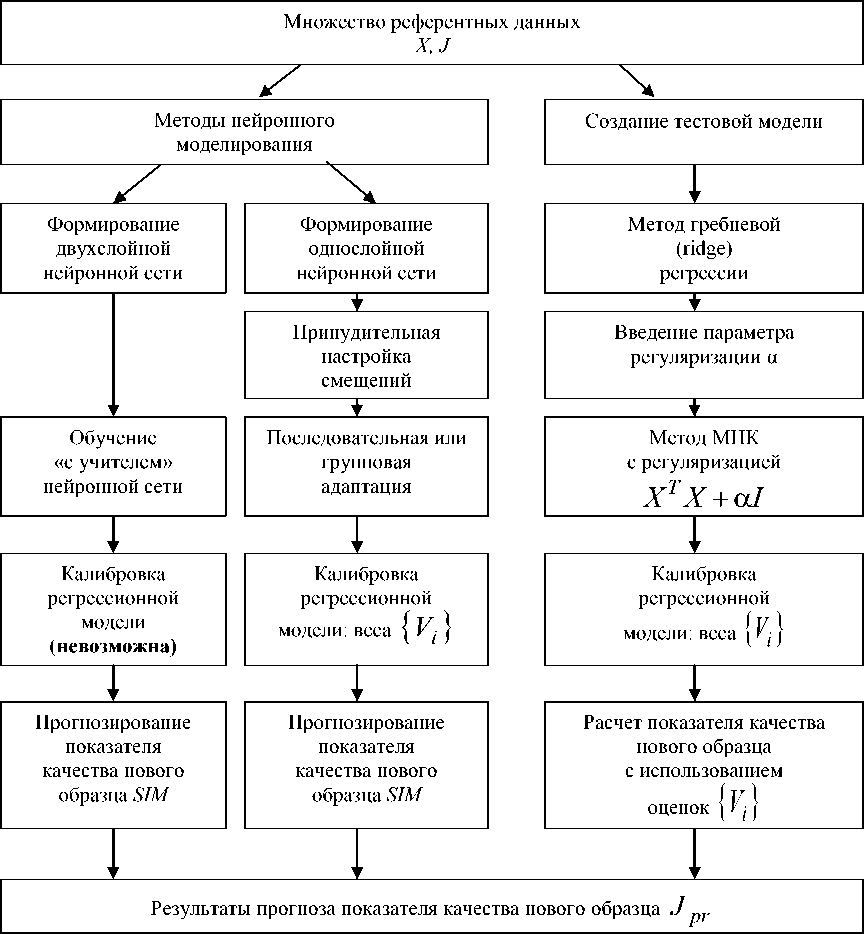
Рисунок 1. Методы прогнозирования обобщенного показателя качества нового объекта экспертизы

Второй метод, метод адаптации, позволяет ограничиться рассмотрением однослойной нейронной сети и осуществить калибровку регрессионной модели. Однако этот метод труднее реализуем, чем метод train с использованием графического интерфейса GUI: при последнем нейронная модель во многом создается автоматически, а процедура adapt требует создания специальных программ на языке MATLAB, называемых М–файлами или М– функциями. Прогнозирование значений показателя J _pr нового образца по-прежнему осуществляется с помощью процедуры sim .

Третий алгоритм (на рисунке 1 представлен справа) осуществляет тестирование полученных с помощью нейронного моделирования результатов. Дело в том, что нейрон- ное моделирование зачастую не гарантирует выполнения принципа общности [1, 3]. Последний заключается в том, что нейронная модель, обученная на одном наборе данных, окажется адекватной при подаче на ее вход данных из другого набора.

Иными словами, предварительно обученная нейронная сеть может просто «не увидеть» данных нового набора. При этом ошибки могут быть не только значительными, но и чрезмерными (100–200 %). Например, при использовании процедуры adapt из-за неправильного выбора параметра скорости адаптации lr для весов нейрона алгоритм просто расходится.

Поэтому при использовании нейронного моделирования абсолютно необходима процедура тестирования полученных результатов с по- мощью другого, «не нейронного» метода. Таким надежным методом представляется метод гребневой (ridge) регрессии, основанный на теории регуляризации некорректно поставленных задач.

Рассмотрим метод адаптации с фиксацией смещений нейронов (AФСН). Как отмечалось ранее, методы «обучения с учителем», реализованные в среде MATLAB с помощью графического интерфейса GUI, обладают следующими недостатками: 1) неоднозначностью результатов моделирования, обусловленной случайным выбором начальных условий; 2) полным несоответствием (даже противоречием) полученных весов w_i исходным весам V_i регрессионной модели в силу эффекта переобучения; 3) нарушением принципа общности — обученная на одном наборе данных нейронная сеть не воспринимает данные нового набора.

В отличие от использования графического интерфейса GUI, для реализации методов адаптации требуется создание программ на языке MATLAB в виде М-файлов или М-функций. Существо нововведений предлагаемого метода AФСН состоит в следующем:

• 1.    Вместо двухслойной нейронной сети для адаптации рекомендуется однослойная нейронная сеть, более полно отвечающая использованию метода характеристических точек, в качестве которых выбираются взвешенные суммы отдельных групп признаков.

• 2.    Для устранения проблемы неоднозначности, вызванной традиционным выбором случайных начальных условий, начальные значения весов и смещений нейронов выбираются нулевыми.

• 3.    Для методологического единства решения прямой и обратной задачи экспертизы на веса и смещения нейронной сети программно накладываются следующие ограничения: веса w^ е [ 0 , 1 ] , а смещения принудительно полагаются равными нулю путем выбора параметра скорости адаптации смещений lr = 0 .

• 4.    Результаты нейронного моделирования часто могут быть недостоверными в силу нарушения принципа общности. Для проверки его соблюдения необходимо обязательное тестирование полученных результатов, например, с помощью метода гребневой регрессии.

Предложенный метод адаптации AФСН может быть реализован в виде двух вариантов:

• 1)    последовательная адаптация нейронной сети;

• 2)    групповая адаптация нейронной сети. Последовательная адаптация была рассмотрена ранее [7]. Поэтому в данной работе мы ограничимся лишь случаем групповой адапта-

• ции для тех же референтных данных X, J, что и в статье [7].

При этом матрица нормированных признаков, соответствующая трем известным объемным извещателям (образцам):

X =

0 , 929

0 , 976

0 , 651

0,460  0,6461

1,000  0,6280

0,539  0,8870

а вектор показателей качества известных извещателей:

J = (1,807  1,681  1,644)T.(5)

Рассмотрим групповую адаптацию нейронной сети . Сформируем однослойную нейронную сеть с линейной функцией активации (рисунок 2), и положим начальные значения весов w_i ¹ и смещения b ¹ равным нулю:

net.b{1}=0.

Кроме того, запретим изменение b ¹ в процессе адаптации командой, означающей приравнивание нулю скорости адаптации смещения lr :

а скорость адаптации весов выберем равной 0,2:

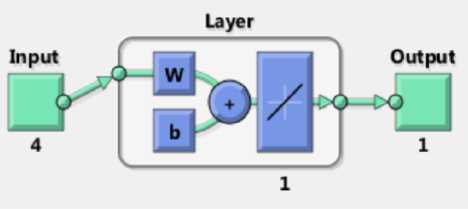
Рисунок 2. Символьная схема однослойной сети с линейной функцией активации f(z) = purelin(z)

Параметр lr в формуле (7) играет решающую роль в определении степени устойчивости алгоритма. Параметр определяется в ходе вычислений экспериментально, и при неправильном выборе алгоритм резко расходится.

На вход нейронной сети одновременно подаются векторы нормированных признаков различных образцов, заданные совершенно иначе, чем в выражении (4) – в виде массива чисел двойной точности:

P =[0.929 0.976 0.651;

0.460 1.000 0.539;

0.646 0.628 0.887;                     (8)

1.000 0.782 0.953],

В качестве вектора целей T был выбран вектор обобщенных показателей (также массив чисел двойной точности):

T =[1.807 1.681 1.644].            (9)

Результаты групповой адаптации с помощью процедуры adapt однослойной нейронной сети приведены на рисунке 3.

После 30 шагов (циклов) адаптации погрешности оценки отдельных показателей J^ - J ₃ равны:

5 J 1 = 0 , 0680 ,

• 5    J 2 = - 0 , 0391 ,  5 J ₃ = - 0 , 0264,    (10)

а усредненный квадрат СКО калибровки равен 0,0023. Как видим, после процедуры адаптации сформированный вектор весов нейрона:

IW(1) = ( 0 , 6147 0 , 2247 0 , 4918 0 , 7483 ) T (11) содержит только неотрицательные значения весов из интервала [0, 1], что соответствует обычной практике экспертных систем [6]. В этом состоит серьезное преимущество метода групповой адаптации перед рассмотренным ранее [7] методом обучения ( train) .

Кроме того, полученный вектор весов (11) оказался сильно коррелированным с исходным вектором V (2), использованным при расчете референтных данных X :

kwv = corr (W,V ) = 0,917. (12)

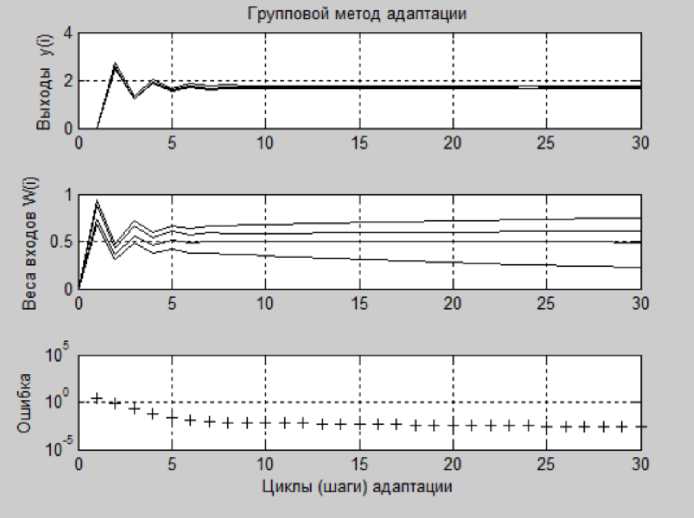
Рисунок 3. Значения выходов, весов нейрона, и ошибки при групповой адаптации нейронной сети

Подав на вход сформированной однослойной сети характеристический вектор нового объемного извещателя «Сокол-Р» (также в виде массива чисел двойной точности) с помощью процедуры моделирования [Y2,pf] = sim(net,P2), получим для нового объекта значение показателя качества     = 1, 5655 с от- pr      , носительной погрешностью 6,93 %.

Сравним методы обучения и адаптации. Для трех рассмотренных выше методов сведем результаты калибровки и прогноза обобщенного показателя качества нового объекта экспертизы в единую таблицу (таблица 1), используя результаты данной работы и статьи [7]. Приведем также для сравнения данные работы тестовой 120

программы, основанной на методе гребневой регрессии.

Как следует из представленных результатов (см. таблицу 1), во всех случаях следует пользоваться предложенными методами последовательной и групповой адаптации ( adapt ) с фиксацией смещений нейронов (АФСН), поскольку при этом имеется возможность восстановления исходной регрессионной модели. При фиксации нулевых смещений нейронов ( b ¹ = 0 ) их найденные веса w¹ приобретают значения из диапазона [0, 1], что обеспечивает методологическое единство решения прямой и обратной задачи экспертизы.

Т а б л и ц а 1

Результаты калибровки и прогноза показателя нового образца

Метод калибровки модели	Восстановление V i	Погрешность калибровки	Прогноз показателя	Погрешность прогноза
Тестовый метод гребневой (ridge) регрессии	+	0,2082	1,565	6,9%
Обучение двухслойной нейронной сети	—	6,371 · 10-10	1,529	4,4 %
Последовательная адаптация методом АФСН	+	0,0019	1,548	5,8 %
Групповая адаптация методом АФСН	+	0,0023	1,566	6,9 %

В тех же практических ситуациях, когда требуется лишь прогнозировать значение обобщенного показателя качества J pr нового объекта экспертизы, а веса и смещения двух