Метод иерархической компрессии индексных изображений

В работе предлагается метод безошибочной компрессии палитровых (индексных) изображений искусственного происхождения. Важным примером таких изображений являются растровые картографические изображения (рис. 1), изображения технических чертежей, диаграмм и т.д. Такие изображения создаются, хранятся и используются с помощью специализированных программных систем, как правило, в виде векторных изображений. Однако в некоторых целях (например, для передачи по Интернет) эти изображения должны быть преобразованы в растровую форму, что делает актуальной задачу их компрессии.

Рис. 1. Примеры картографических изображений

Как правило, изображения рассматриваемого класса содержат однородные области, очерченные контуром и залитые одним цветом, (либо некоторой текстурой с малым количеством цветов), некоторые знаки, линии, текст. При этом количество цветов на таких изображениях обычно ограничено несколькими десятками. На подобных изображениях практически не встречаются плавные изменения яркости, характерные для полутоновых и цветных (RGB) изображений.

Наиболее распространенные методы сжатия изображений не являются безошибочными и основаны на том, что небольшое изменение значения пиксела приводит к незначительному визуальному изменению изображения. Для компрессии палитровых изображений необходимо применять безошибочное сжатие, поскольку в них вместо значений яркости используются индексы (как правило, в формате байт на пиксел изображения), определяющие цвет в RGB-координатах с помощью отдельно сохраняемой таб- лицы (палитры). В результате ошибка в значении пиксела всего на единицу может привести к смене цвета, например, с синего на красный.

В настоящее время наиболее часто используются следующие стандарты безошибочного сжатия изображений: GIF[1], Lossless JPEG [2], JBIG [3]. Однако большинство из них не учитывают специфики изображений рассматриваемого класса и, следовательно, не могут обеспечить необходимую степень компрессии.

1.    Краткое описание метода и базового алгоритма

Идея предлагаемого метода заключается в иерархическом представлении изображения в виде набора матриц или иерархических уровней (ИУ) уменьшенного размера и кодировании только информации, необходимой для восстановления очередного ИУ по восстановленным значениям предыдущих ИУ.

Пусть исходное изображение является матрицей x ( n 1 , n 2 ) размером N 1 x N 2 , текущий l -ый уровень представляет собой матрицу x ⁽ l ) ( n₁, n 2 ) размером

NN

—_? x —- , где M , M_? - коэффициенты масштаби- _Ml _Ml         1   2

рования изображения при переходе к очередному ИУ. На текущем уровне строится гистограмма значений пикселов в блоках размером M 1 x M2, составляется список блоков по убыванию значений гистограммы и в очередной l +1 -ый уровень вместо каждого блока записывается соответствующий индекс блока из списка. Очевидно, что для восстановления всех ИУ (и, следовательно, исходного изображения) достаточно иметь все списки, сформированные на уровнях, и матрицу старшего уровня раз-NN мером —1- x —-, где L - количество ИУ.

M ^L M ^L

Компрессия изображения обеспечивается благодаря наличию большого количества одинаковых блоков на изображениях рассматриваемого класса, информация о которых в формируемых списках записывается однократно. Кроме того, для получения большей степени сжатия списки подвергаются ста- тистическому кодированию (например, алгоритмом арифметического кодирования [4]).

Для описания алгоритма сжатия на основе предлагаемого метода примем следующие допущения. Во-первых, ограничимся рассмотрением блоков размеров 2 x 2. Во-вторых, компрессируемое изображение (особенно в случае больших размеров, что характерно для изображений рассматриваемого класса) может при необходимости разбиваться на непересекающиеся фрагменты, каждый из которых компрессируется независимо от других. Далее рассматриваем в качестве изображения независимо обрабатываемые фрагменты, размеры которых являются степенью двойки, и определяются с учетом ограничений конкретного алгоритма обработки.

Алгоритм компрессии заключается в последовательном формировании и сжатии списков значений четверок для всех ИУ, начиная с нулевого уровня x ^{( 0 )}( n_b n ₂ ) = x ( n_b n ₂ ) . Пусть на каждом уровне формируется (и упорядочивается по частоте в порядке убывания) список значений четверок C ^{( 1} ) = { c k ‘ ) ( 0 ), C k l ) ( 1 ), C k l ) ( 2 ) , C k l ) ( 3 ) } k = 0 . Тогда отсчеты следующего ИУ формируются по правилу:

x ^{( 1 + 1 )} ( П 1 , n 2 ) = к ,

' x ^{( 1} ) (2 n _b2 n 2 ) = C k^{1 )}(0)

x ^{( 1} ) (2 n + 1,2 n 2 ) = C k¹ ) (1)    .

k : 1

x ^{( 1} ) (2 n i ,2 n 2 + 1) = C k¹ ) (2)

. x ^{( 1} ) (2 n + 1,2 n ₂ + 1) = C k¹ ) (3)

Матрица старшего уровня x(L)(n1, n2), как и списки C(1), 0 < 1 < L , подвергается статистическому кодированию и сохраняется в массиве сжатой информации.

Параметрами данного алгоритма являются размеры фрагмента и количество ИУ, определяемые с учетом ограничений K ^{( 1} ) <  255, 2 ^L <  N 1 ,2 ^L <  N ₂. Следует отметить, что выполнение первого ограничения вытекает из условия сохранения всех данных (матриц ИУ и списков) в байтовом формате.

При декомпрессии матрица старшего уровня и списки ИУ декодируются, после чего последовательно восстанавливаются матрицы всех ИУ:

x ^{( 1} ) (2 n 1 ,2 n 2 ) = C k¹ ) (0)

x ^{( 1} ) (2 n + 1,2 n 2 ) = C k¹ ) (1)

x ^{( 1} ) (2 n 1 ,2 n ₂ + 1) = C k¹ ) (2) ^, x ^{( 1} ) (2 n 1 + 1,2 n ₂ + 1) = C k¹ ) (3)

если x ^{( 1 + 1 )} ( n 1 , n ₂) = k .

0	4	2	4
0	0	0	2
0	3	4	1
3	4	1	1

0	4	0	0	1
2	4	0	2	1
0	3	3	4	1
4	1	1	1	1

0	0
0	0

Однако непосредственное применение этого алгоритма неэффективно вследствие огромного количества комбинаций значений пикселов в блоках, значительная часть которых может встретиться однократно на изображении (особенно на границах областей, линий, символов). Ниже предлагаются пути сокращения объемов данных в списках, формируемых на ИУ, что приводит к руемых на ИУ, что приводит к значительному повышению эффективности компрессии.

2.    Повышение эффективности базового алгоритма

Использование одного индекса для однократно встречаемых блоков

Пусть T ^{( 1} ) - количество четверок в списке C ^{( 1} ) , с частотой более единицы, т.е. частоты элементов Ck¹ ) , k >  T ^{( 1} ) равны единице.

Тогда использование правила для формирования матрицы следующего ИУ x (1+1)( n1,n 2)

; ^k , ^k <  т ^{( 11}

T , k >= T ^{( 11}

' x ^{( 1} ) (2 n 1 ,2 n 2 ) = C k¹ ) (0)

, x ^{( 1} ) (2 n 1 + 1,2 n 2 ) = C k¹ ) (1) x ^{( 1} ) (2 n 1 ,2 n 2 + 1) = C k¹ ) (2) . x ^{( 1} ) (2 n 1 + 1,2 n ₂ + 1) = C k¹ ) (3)

приведет к созданию более однородного изображения и значительному уменьшению длины списка на следующих ИУ.

Введение порогового значения T ^{( 1} ) позволяет смягчить ограничение на размеры фрагмента, в данном случае требуется выполнение условия T ^{( 1} ) < 255.

На рисунке 2 показан пример работы данного алгоритма для изображения размером 8 x 8. Матрица x ⁽⁰ представляет исходное изображение; матрицы x ⁽¹⁾, x ⁽²⁾ и списки C ⁽⁰, C ⁽¹⁾ получены с помощью правила (1).

x ⁽⁰⁾                      C ⁽⁰⁾

0	0	1	0	0	0	1	0
0	0	0	1	1	1	0	0
0	0	0	0	0	0	0	0
0	0	0	0	0	0	1	1
0	0	0	0	0	1	2	2
0	0	0	1	1	2	2	2
0	0	1	2	2	2	2	2
0	1	2	2	2	2	2	2

0	0	0	0	5
2	2	2	2	3
0	0	1	1	2
0	0	0	1	2
1	0	0	1	1
1	0	0	0	1
0	1	1	2	1
1	2	2	2	1

x ⁽¹⁾                C ⁽¹⁾                  x ⁽²⁾

Рис. 2. Пример кодирования изображения для

N 1 = N ₂ = 8

При декомпрессии четверка уровня x ^{( 1 )} соответствует элементу списка C_k ^{( 1 )} , где

\ x ^{( 1 + 1)}( n_b n 2 ), x ^{( 1 + 1)}( n_b n 2 ) <  T ^{( 11}

k = S                                         ,

[ x ^{( 1 + 1)} ( n 1 , n 2 ) + P , x ^{( 1 + 1)} ( n 1 , n 2 ) = T ^{( 1 1}

P - количество обработанных x ^{( 1 + 1)}( n 1 ,n 2 ) = T ^{( 1} ) .

Использование шаблонов

Объем списка C^(l) можно уменьшить за счет использования шаблонов. Вводится 8 шаблонов (рис. 3) с целью более эффективного кодирования элементов списка с числом различных значений не более 2. Большинство таких элементов имеет достаточно высокие значения частот.

Рис. 3. Шаблоны значений отсчетов четверок с числом различных значений не более двух

Те элементы списка, которые соответствуют одному из шаблонов, вместо 4-х байт кодируются 3-мя байтами: номером шаблона и двумя цветами шаблона. Для реализуемости декомпрессии необходимо переупорядочить список таким образом, чтобы в начале шли элементы, к которым можно применить шаблон. Дополнительно сохраняется количество элементов, закодированных с использованием шаблонов. К элементам, порядковые номера которых больше порога, не применяется кодирование шаблона, так как для восстановления необходимо сохранять их порядок.

Адаптивный выбор порога

Выбор порога T^(l) существенно влияет на степень компрессии. При уменьшении величины порога T^(l) увеличивается объем списка C^(l) , но при этом матрица следующего уровня становится более однородной, что улучшает компрессию. Следовательно, выбор оптимального порога может обеспечить значительное повышение эффективности сжатия.

Для оценки сжатия данных текущего и следую- щего уровня можно использовать энтропию, вычисленную для данных списка текущего уровня и значений матрицы следующего уровня (хотя на следующем уровне будет сжиматься не матрица, а новый список, предполагаем связь между их энтропиями). Для выбора оптимального значения порога предлагается использовать критерий:

H ( c ^{( 1} ) , T ^{( 1} ) )■ V ( c ^{( 1} ) , T ^{( 1} ) ) +

+ aH ( x ^{( 1} ) , T ^{( 1} ) )■ V ( x ^{( 1} ))— T ₍ l ) >  min ,

где H – энтропия, T (l) – значение порога, начиная с которого элементы списка кодируются одним числом, V(c(1), T(1)) - объем данных списка текущего уровня, V(x(1)) - объем данных матрицы следующего уровня, a – параметр (значение подбирается на этапе настройки алгоритма для заданного класса изображений).

Пусть T_o ⁽ _p ^l _t ⁾ – оптимальное значение параметра оптимизации T ^{( l )} критерия (2). После определения T_o ⁽ _p ^l _t ⁾ строится список, в котором элементы с частотой, меньшей или равной T_o ⁽ _p ^l _t ⁾ кодируются одним числом и заносятся в список в порядке обхода.

В процессе оптимизации, частоты T ^{( l )} , индексы которых в списке больше 256, не рассматриваются. Таким образом, алгоритм не накладывает ограничений на размер компрессируемого фрагмента.

Предлагаемый алгоритм дает значение близкое к оптимальному, которое может быть получено только путем полного перебора всех возможных значений порога (от 0 до K ^{( 1} ) ), однако трудоемкость предлагаемого алгоритма значительно ниже.

3.    Экспериментальные исследования

Для оценки эффективности предложенного метода компрессии палитровых изображений искусственного происхождения были проведены экспериментальные исследования на тестовых изображениях, полученных из цифровых карт. Компрессия производилась на 14 изображениях размера 1024 x 1024 различной сложности и с разным количеством цветов.

Производилось сравнение разработанного метода (в 4 вариантах реализации алгоритма сжатия) с такими методами безошибочной компрессии, как GIF, JPEG-LS [5] и HGI (метод компрессии на основе иерархической сеточной интерполяции [6, 7]). Кроме того, производилось сравнение с широко распространенным архиватором WinZIP (версия 8.0, режим наилучшего сжатия).

Для предлагаемого метода, исходя из ограничений, накладываемых алгоритмами на размер изображения, при необходимости производилось разбиение изображений на блоки.

В таблице приведены размеры (в байтах) сжатых изображений P1,P2,…P14 для исследуемых методов сжатия. В последних двух строках таблицы содержатся суммарный объем сжатых файлов и объем сжатых файлов относительно исходных изображений. Отдельно приводится диаграмма объема сжатых файлов относительно исходных изображений (рис. 4).

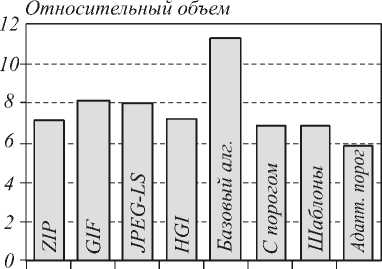
Рис. 4. Объем сжатых файлов относительно исходных изображений

	ZIP	GIF	JPEG-LS	HGI	Базовый алгоритм	С порогом	С шаблонами	Адаптивный порог
P1	14611	18928	17475	25889	41466	14166	14142	11529
P2	16602	20619	17857	21149	38203	10115	10172	9520
P3	19824	29389	33915	43769	55748	21975	22191	17886
P4	47294	60034	53373	48051	87998	44088	43980	35293
P5	54686	69253	65814	54293	101927	63353	63234	44377
P6	59362	67435	59901	59600	93945	57185	57613	45210
P7	70717	80633	77570	67008	109483	68558	68916	56824
P8	78666	85156	79543	77529	119587	73974	74584	61072
P9	93937	100754	90507	89716	133814	83023	83469	68572
P10	103538	108372	108195	97900	151260	95276	95946	79364
P11	104725	124219	122482	100401	159420	104005	103917	93713
P12	117243	124559	158338	121533	178372	117494	117093	106471
P13	123153	130137	121559	116655	178691	114054	114185	99938
P14	139952	160949	158991	133297	203983	134754	134650	124686
Сумма	1044310	1180437	1165520	1056790	1653897	1002020	1004092	854455
Относительный объем, %	7,11%	8,03%	7,93%	7,19%	11,25%	6,81%	6,83%	5,81%

Таблица. Результаты экспериментальных исследований

Как и ожидалось, непосредственная реализация базового алгоритма не обеспечивает приемлемой эффективности сжатия. Однако небольшая модификация алгоритма с фиксированием одного индекса для повторяющихся блоков уменьшает объем сжатых данных на 4,44%. Исследования показали, что использование шаблонов не привело к дальнейшему улучшению алгоритма (лучшие показатели имеются только для отдельных изображений), однако пути совершенствования алгоритма в этом направлении далеко не исчерпаны.

Наибольшее сжатие из рассмотренных вариантов реализации предлагаемого метода дает алгоритм с адаптивным выбором порога. Этот алгоритм обеспечивает лучшее сжатие как по сравнению с известными стандартами GIF (в среднем на 2,22%) и JPEG-LS (в среднем на 2,12%), так и с архиватором WinZIP (в среднем на 1,20%).

Предлагаемый метод не является симметричным (по отношению времени компрессии / декомпрессии) – декомпрессия происходит быстрее, в особенности для варианта с адаптивным выбором порога. Кроме того, при декомпрессии возможно частичное восстановление изображения в требуемом масштабе (мультиразрешение), что делает метод привлекательным для приложений, связанных с передачей крупноразмерных изображений искусственного происхождения через Интернет.

Работа выполнена при поддержке Министерства образования РФ, Администрации Самарской облас- ти и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы "Фундаментальные исследования и высшее образование" (BRHE); а также при поддержке Российского фонда фундаментальных исследований (РФФИ), проект № 04-01-96507.