Метод использования нечетких гиперграфов для оценивания структурно-технологической живучести элементов системы управления ориентацией автоматических космических аппаратов

Эффективность работы автоматических космических аппаратов (АКА) при выполнении полетного задания во многом зависит от надежности работы бортовых систем (БС) бортового комплекса управления (БКУ) АКА. Известно [1], что все функциональные элементы (ФЭ) БС задействуются неравномерно, при этом их технологические циклы зачастую не совпадают. Увеличение сроков активного существования АКА возможно путем обеспечения живучести функционирования их БС как в номинальных условиях полета, так и при возникновении расчетных и нерасчетных нештатных ситуаций.

При возникновении расчетных нештатных ситуаций или «нормальных» условий полета для оценивания живучести БС АКА, как правило, применяют [1–3] имитационные модели орбитального движения АКА и его функционирования по целевому назначению с использованием статистической обработки результатов эксплуатации уже созданных АКА. При проектировании новых АКА, существенно отличающихся от ранее созданных, такой подход не всегда приемлем. Особенно в условиях нерасчетных нештатных ситуаций модели и методы, применяемые в теории надежности, становятся неприменимы для обеспечения живучести БС АКА, что требует разработки новой методики ее оценивания.

Важным и неотъемлемым условием изучения возможностей БС АКА [4–6]

является проведение анализа и оценивания его структурных состояний, отражающих как функциональные, так и технологические особенности управления АКА.

При этом значения частных показателей качества функционирования (в частности, показателей структурнофункциональной и структурно-технологической живучести) БС АКА в каждом состоянии (конфигурации) зависят от следующих факторов:

• •    множества отказавших, работоспособных, частично работоспособных ФЭ;

• •    распределения технологических операций;

• •    перераспределения этих операций между работоспособными или частично работоспособными ФЭ.

С целью определения роли конкретных ФЭ БС в обеспечении структурной живучести конфигураций БС АКА следует проводить анализ значений показателей структурно-технологической живучести, оценивающих степень участия ФЭ и подсистем БС в технологических операциях управления АКА при различных сценариях реализации программы полета. Далее под структурнотехнологической живучестью будем понимать частное свойство живучести БС АКА, характеризующее способность БС обеспечивать гарантированное выполнение комплекса операций, входящих в состав технологического цикла управления АКА, при целенаправленных и/или индифферентных возмущающих внешних воздействиях. В качестве примера такой БС выберем систему управления ориентацией (СУО).

Типовая технология управления ориентацией АКА дистанционного зондирования Земли (ДЗЗ), представленная в работе [7], при штатном его функционировании включает следующие технологические режимы (операции) (таблица):

• •    «Построение орбитальной системы координат (ОСК)» — «грубая» ориентация;

• •    «Поддержание ориентации АКА в ОСК» — «точная» ориентация;

• •    «Приведение АКА в ориентированное на Солнце положение».

Для выполнения указанных режимов используются различные чувствительные элементы (ЧЭ) и исполнительные органы (ИО), включающие одноосные измерители угловой скорости (ОИУС), управляющие двигатели-маховики (УДМ), датчики системы спутниковой навигации (ССН), приборы ориентации по Земле (ПОЗ), оптические звездные датчики (ОЗД), магнитометры (МА), электромагниты (ЭМ).

При этом следует отметить, что частота применения технологических режимов ориентации АКА при выполнении типовых операций по приему (передаче) различной информации (специальной, телеметрической, баллистической, командно-программной), циркулирующей в контурах управления АСУ КА в течение технологического цикла управления (ТЦУ) АКА, зависит от целей полетного задания. В данной статье будем считать, что частота задействования режима «грубой» ориентации составляет 40%; «точной» ориентации — 50%; «ориентации на Солнце» — 10%.

Рассмотрим отдельно каждый режим ориентации, а также задействование бортовой аппаратуры автоматического КА при его выполнении.

Режим «грубой» ориентации характеризуется ориентацией связанных осей АКА в орбитальной системе координат (ОСК):

• •    Ox 1 x 2 x 3 — связанная система координат (ССК), O — центр масс АКА, ее оси совпадают с главными центральными осями инерции АКА;

• •    OX 1 X 2 X 3 — орбитальная система координат (ОСК), ось OX 1 лежит в плоскости орбиты и направлена по нормали к радиус-вектору в сторону движения АКА, ось OX 3 — по радиус-вектору центра масс АКА, OX 2 дополняет систему до правой [8].

Прибор ОИУС измеряет угловую скорость по одной оси. Будем считать, что на АКА приборы ОИУС с 1-го по 3-й расположены по осям связанного базиса и предназначены для измерения углов ориентации по каналам крена ( Ox 1), рыскания ( Ox 2) и тангажа ( Ox 3), а ОИУС4 расположен так, чтобы иметь возможность измерения угловой скорости в случае отказа одного из ОИУС1, ОИУС2, ОИУС3.

Рассмотрим наиболее часто встречающиеся способы построения и поддержания ориентации. Построение ориентации осуществляется с использованием датчика определения координат центра Земли (ПОЗ), управление от которого ведется одновременно по каналам крена ( Ox 1) и тангажа ( Ox 3). Приведение ориентации по каналу рыскания производится с использованием измерителя угловой скорости по каналу рыскания (ОИУС2 или ОИУС4).

Для поддержания ориентации в ОСК применяется бесплатформенная инерциально-навигационная система (БИНС) в составе СУО, для реализации которой используются измерители угловой скорости по всем трем каналам. Датчики внешней ориентации ССН и ОЗД периодически включаются для проведения коррекции БИНС (компенсации угловых ошибок ориентации).

При определении положения ССК АКА относительно ОСК достаточно нахождения углов отклонения оси Ox 2 ССК от местной вертикали и измерения угловой скорости по оси Ox 1 или по оси Ox 3 CCК. Для этих целей могут быть использованы один ПОЗ и приборы ОИУС по оси Ox 1 или по оси Ox 3 CCК.

Ориентация АКА во всех трех режимах («грубой» ориентации, «точной», «ориентации на Солнце») осуществляется с помощью УДМ, как основных исполнительных органов АКА, и системы из трех электромагнитов совместно с магнитометром для сброса кинетического момента, накопленного УДМ. При этом три УДМ расположены по осям АКА (основные), а четвертый (резервный) расположен так, чтобы создавать управляющий момент сразу по трем осям [8]. Один из вариантов проведения «грубой» ориентации в ОСК [9] возможен при условии работоспособности одного основного и одного резервного УДМ, а сброс кинетического момента проводится на трех электромагнитах. Другим вариантом для «грубой» ориентации является использование любых трех УДМ и двух из трех электромагнитов для сброса кинетического момента.

Переориентация АКА с ОСК в заданную инерциальную систему координат (ИСК) характеризуется не только требованиями к точности определения углового положения аппарата в ОСК и ИСК после разворота, но также и к скорости переориентации АКА и сбросу накопленного кинетического момента. Для этих целей используется технологическая схема, в которой задействуются минимум три работающих УДМ и три ЭМ. При этом для управления ориентацией применяются три любые ОИУС. Кроме того, в зависимости от заданной системы координат для определения положения АКА используются ПОЗ или ОЗД в совокупности с датчиковой аппаратурой ССН.

Режим «ориентация на Солнце» характеризуется тем, что солнечные батареи (СБ) АКА должны быть сориентированы нормалью к рабочей поверхности на Солнце. Для определения направления нормали СБ на Солнце применяются датчики ССН. При построении ориентации СБ на Солнце используются измерители вектора угловой скорости по трем осям. После переориентации аппарата с «солнечной ориентации» в ОСК или ИСК задействуются датчики внешней информации ПОЗ и ОЗД. При этом используется конфигурация из трех УДМ с применением ЭМ для разгрузки от накопленного кинетического момента.

Сценарий одного из описанных выше вариантов применения технологических режимов ориентации АКА представлен в таблице.

Для анализа показателя структурнотехнологической живучести БС АКА предлагается использовать математический аппарат нечетких гиперграфов — обобщение нечеткого графа, в котором каждым ребром (технологическим режимом) может соединяться любое подмножество вершин (ФЭ БС), а степень принадлежности вершины ребру характеризует степень задействования ФЭ при проведении данной технологической операции. Так, например, степень задействования каждого ОИУС при проведении технологического режима «ориентации на Солнце» равна 0,75, а также каждого МА равна 0,5 и каждого ЭМ — 0,67.

Использование такого формального представления технологических режимов позволяет проводить анализ структурнотехнологических свойств СУО АКА. При этом путем вычислений определяются значения показателей интенсивности применения элементов в тех или иных технологических процессах и неравномерности участия элементов в различных технологических циклах управления. Это позволяет оценить уровень структурно-технологической живучести как отдельных ФЭ СУО, так и СУО в целом при разработке новых технологий управления конфигурацией и реконфигурацией БС АКА.

нечеткий гиперграф режимов ориентации ака и операция его дифференцирования

Обозначим нечеткий гиперграф через H = 〈X, U, µ〉, где X = {xi, i = 1, 2, …, n} — множество типовых ФЭ БС (в частности, элементов системы управления ориентацией АКА: ОИУС, УДМ, ССН, ПОЗ, ОЗД, МА, ЭМ); U = {ul ⊆ X, l = 1, 2, …, m} — множество ребер гиперграфа (технологических режимов режимы ориентации автоматического космического аппарата

Тип элемента	ОИУС				УДМ				ССН	ПОЗ		ОЗД		МА		ЭМ
№ элемента	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Режим «грубая» ориентация	1 из 2-х		—		3 из 4-х				—	1 из 2-х		—		1 из 2-х		2 из 3-х
	—								1	—		1 из 2-х
Режим «точная» ориентация	3 из 4-х				3 из 4-х				—	1 из 2-х		—		1 из 2-х		1	1	1
									1	—		1 из 2-х
Режим «ориентация на Солнце»	3 из 4-х				3 из 4-х				—	1 из 2-х		—		1 из 2-х		2 из 3-х
										—		1 из 2-х

Примечание. ОИУС1 расположен по оси Ox 1; ОИУС2 — по оси Ox 3; ОИУС3 — по оси Ox 2; ОИУС4 расположен по трем каналам; УДМ1, УДМ2, УДМ3 — основные; УДМ4 – резервный. Сокращения см. в тексте.

с учетом частоты их задействования); ц: Xх U^[0, 1] — функция степени (потенциальной возможности) задействования ФЭ при проведении той или иной технологической операции. Нечеткий гиперграф режимов ориентации H удобно обозначать матрицей инцидентности Q = ||qliHmxn, где qi — степень задействования i-го ФЭ при выполнении l-го технологического режима. Тогда обобщенное задействование i-го ФЭ в ТЦУ АКА можно обозначить вектором →υi = (q1i, q2i, …, qmi), данный вектор характеризует направление активности ФЭ БС и интенсивность этой активности | иil 2. Для вычисления интенсивности совместного задействования двух произвольных ФЭ в ТЦУ с учетом направления их активности можно использовать скалярное произведение векторов обобщенного задействования (→υi, →υj), i, j = 1, 2, …, n.

Для проведения анализа структурнотехнологической живучести БС АКА введем понятие матрицы интенсивности задействования ФЭ в ТЦУ F = ||Д.|| nxn, элементы которой fj(Vi * j) равны интенсивности совместного задействования ФЭ в ТЦУ, а fii = I иi12 — интенсивность собственного задействования ФЭ в ТЦУ. При этом следует отметить, что максимальная интенсивность собственного задействования ФЭ в ТЦУ fmax = m. Матрица F может быть вычислена из матрицы инцидентности Q по формуле F = QT х Q, где QT — транспонированная матрица инцидентности.

Далее по аналогии с производной гиперграфа, введенной в работах [6, 10, 11]

и основанной на использовании понятия частоты участия элементов в различных событиях (под событием понимается ребро, связывающее элементы гиперграфа), введем понятие производной нечеткого гиперграфа.

Производной д H / д U нечеткого гиперграфа H по событию U называется граф, каждая пара вершин которого ( v_i , v_j ) взвешена отношением интенсивности ( f_ii – f_ij ) + ( f_jj – f_ij ) их несовместного участия в событии U (интенсивность несовместного задействования ФЭ) к интенсивности f_ij совместного задействования ФЭ в событии U :

∂ H

"U^ v ) =

fti - ff ++fj f-ij

Другими словами, происходят собы-

на элементах графа H

тия U — технологические режимы ориентации, а производная д H/дU будет характеризовать степень равномерности совместного задействования ФЭ в ТЦУ.

исследование уровня структурно-технологической живучести конфигурации Суо ака

Пусть типовой технологический цикл управления АКА включает в себя 40 режимов ориентации, из них: режим «грубой» ориентации задействуется 16 раз (40%), «точной» ориентации — 20 раз (50%), а режим «ориентация на Солнце» — 4 раза (10%).

В этом случае матрица инциденций данного нечеткого гиперграфа может иметь вид u8

u ₉

u ₁

^u 16

^u 17

^u 36

^u 37

^u 38

^u 39

^u 40

Q = u26

^u 27

x 1 0,5	x 2 0,5	x 3 0	x 4 0	x 5 0,75	x 6 0,75	x 7 0,75	x 8 0,75	x 9 0	x 10 0,5	x 11 0,5	x 12 0	x 13 0	x 14 0,5	x 15 0,5	x 16 0,67	x 17 0,67	x 18 0,67
0,5	0,5	0	0	0,75	. 0,75	. 0,75	. 0,75	. 0	0,5	0,5	0	0	0,5	0,5	0,67	0,67	0,67
0	0	0	0	0,75	0,75	0,75	0,75	1	0	0	0,5	0,5	0,5	0,5	0,67	0,67	0,67
0	0	0	0	0,75	. 0,75	. 0,75	. 0,75	. 1	. 0	0	0,5	0,5	0,5	0,5	0,67	0,67	0,67
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	0	0,5	0,5	0	0	0,5	0,5	1	1	1
0,75	0,75	0,75	0,75	0,75	. 0,75	. 0,75	. 0,75	. 0	0,5	0,5	0	0	0,5	0,5	1	1	1
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	1	0	0	0,5	0,5	0,5	0,5	1	1	1
0,75	0,75	0,75	0,75	0,75	. 0,75	. 0,75	. 0,75	. 1	. 0	0	0,5	0,5	0,5	0,5	1	1	1
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	0	0,5	0,5	0	0	0,5	0,5	0,67	0,67	0,67
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	0	0,5	0,5	0	0	0,5	0,5	0,67	0,67	0,67
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	0	0	0	0,5	0,5	0,5	0,5	0,67	0,67	0,67
0,75	0,75	0,75	0,75	0,75	0,75	0,75	0,75	0	0	0	0,5	0,5	0,5	0,5	0,67	0,67	0,67

Тогда		матрица		интенсивности			задей-		относительно				главной		диагонали следую-
ствования		ФЭ	в ТЦУ F =		| ^|	8×18 принимает			щий симметричный вид:
	x 1	x 2	x 3	x 4	x 5	x 6	x 7	x 8	x 9	x 10	x 11	x 12	x 13	x 14   x 15		x 16	x 17	x 18
x 1	15,5	15,5	13,5	13,5	16,5	16,5	16,5	16,5	7,5	6,5	6,5	4,5	4,5	11	11	19,69	19,69	19,69
x 2		15,5	13,5	13,5	16,5	16,5	16,5	16,5	7,5	6,5	6,5	4,5	4,5	11	11	19,69	19,69	19,69
x 3			13,5	13,5	13,5	13,5	13,5	13,5	7,5	4,5	4,5	4,5	4,5	9	9	17,01	17,01	17,01
x 4				13,5	13,5	13,5	13,5	13,5	7,5	4,5	4,5	4,5	4,5	9	9	17,01	17,01	17,01
x 5					22,5	22,5	22,5	22,5	13,5	7,5	7,5	7,5	7,5	15	15	25,05	25,05	25,05
x 6						22,5	22,5	22,5	13,5	7,5	7,5	7,5	7,5	15	15	25, 05	25,05	25,05
x 7							22,5	22,5	13,5	7,5	7,5	7,5	7,5	15	15	25,05	25,05	25,05
x 8								22,5	13,5	7,5	7,5	7,5	7,5	15	15	25,05	25,05	25,05
F = х 9 x 10									18	0 5	0 5	9 0	9 0	9 5	9 5	15,36 8,35	15,36 8,35	15,36 8,35
x 11											5	0	0	5	5	8,35	8,35	8,35
x 12												5	5	5	5	8,35	8,35	8,35
x 13													5	5	5	8,35	8,35	8,35
x 14														10	10	16,7	16,7	16,7
x 15															10	16,7	16,7	16,7
x 16																28,97	28,97	28,97
x 17																	28,97	28,97
x 18																		28,97

Произведем вычисление производной нечеткого гиперграфа:

∂ H

∂ U

0,000 0, 000

0, 000

0,148

0,148

0, 000

0,148 0,148 0, 000 0, 000

0,303

0,303

0, 666

0, 666

0, 000

0,303

0,303

0,666

0,666

0, 000

0, 000

0,303

0,303

0,666

0, 666

0,000

0, 000

0, 000

0, 303

0, 303

0, 666

0, 666

0,000

0, 000

0,000

0,000

2, 466 2, 466

2, 200 2,, 200 1,000 1,000 1,000

1, 000 0, 000

1,153

1,153

2,111

2,111

1,666

1, 666

1, 666

1, 666

1,153

1,153

2,111

2,111

1, 666

1,666

1,666

1,666

2,555

2,555

2,111

2,111

1, 666 1,666

1,666 1, 666 0,555

2,555

2,555

2,111

2,111

1,666

1,666

1, 666

1, 666

0, 555

Если (v, v) = ∞, то ФЭ совместно ∂U i j не задействуются при выполнении ТЦУ.

Если же _{∂ U} ( v_i , v_j ) = 0, то направление и интенсивность активности задействования двух ФЭ в проведении ТЦУ

0,318 0,318 0, 258 0, 258 0, 258 0,318 0,318 0, 258 0, 258 0, 258 0, 611 0, 611 0, 497 0, 497 0,497 0, 611 0, 611 0, 497 0, 497 0, 497 1,666 1, 666 0, 055 0, 055 0,055 1,666 1, 666 0, 055 0, 055 0,055 1,666 1,666 0,055 0, 055 0, 055 1,666 1,666 0,055 0, 055 0, 055 1,111 1,111 1,058 1, 058 1, 058 1,000 1, 000 2,069 2, 069 2, 069 1,000 1, 000 2,069 2,069 2,069 1, 000 1,000 2, 069 2,069 2,069 1, 000 1,,000 2, 069 2,069 2, 069 0, 000 0, 000 0,334 0,334 0,334

0, 000 0,334 0,334 0,334

0, 000 0, 000 0, 000

0, 000 0, 000

0, 000

полностью совпадают, т. е. данные ФЭ всегда только совместно участвуют в ТЦУ АКА. В этом случае на графе производной эти два ФЭ можно представлять одной вершиной, следовательно, число вершин графа производной может быть меньше числа вершин исходного гиперграфа режимов ориентации АКА.

Граф производной представлен на рис. 1.

0,, 000

0, 000

0, 000

0, 000

0, 000

0, 000

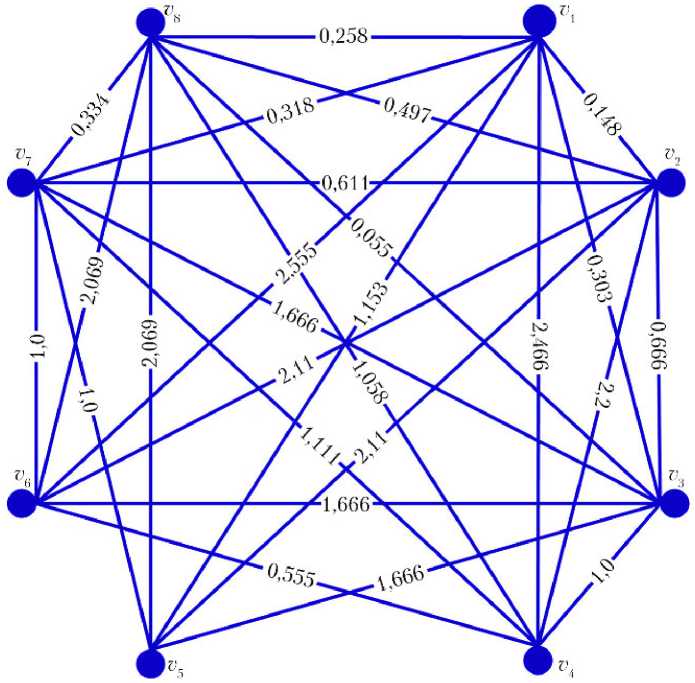
Рис. 1. Граф производной нечеткого гиперграфа

(28,97 + 28,97 – 2·4,5)

≅ 10,88.

4,5

Произведя нормировку значений матрицы смежности ∂H производной гиперграфа, ∂U

можно построить нечеткое отношение технологической независимости ФЭ БС при проведении ТЦУ АКА ^Z = II z j ¹ k x k ( ^k — число вершин графа производной; z_ij — независимость вершин графа производной при выполнении технологических режимов ориентации АКА)

следующим образом.

Шаг 0 . Вначале все соответствуют вершинам нечеткого гиперграфа.

v

i x i

Шаг 1. Если элемент матрицы     (vi, vj) = 0 (i ≠ j),

∂ U

На рис. 1 вершины v ₁, v ₂, v ₃, v ₄, v ₅, v ₆, v ₇, v ₈ производной включают в себя следующие ФЭ: v ₁ = { x ₁, x ₂}; v ₂ = { x ₃, x ₄}; v ₃ = { x ₅, x ₆, x ₇, x ₈}; v ₄ = { x ₉}; v ₅ = { x ₁₀, x ₁₁}; v ₆ = { x ₁₂, x ₁₃}; v ₇ = { x ₁₄, x ₁₅}; v ₈ = { x ₁₆, x ₁₇, x ₁₈} нечеткого гиперграфа.

Кроме того, при увеличении значения ∂ H

то вершины v_i , v_j объеди няются в одну вершину графа.

Шаг 2. Если элемент

-

матрицы

^{∂ H}

_{∂ H                             dU} ( v _i , v _j )

0 <     ( v_i , v_j ) < ∞, то z_ij = 1 –

^β max

.

_{∂ U} ( v_i , v_j ) интенсивность совместного за действования ФЭ СУО при проведе

-

-

нии ТЦУ АКА уменьшается. Другими словами, чем меньше совместное задействование ФЭ СУО при проведении ТЦУ, тем меньше зависят от него другие ФЭ. Определим, какое максимальное значение, отличное от ∞, могут принимать элементы матрицы .

∂ U

Очевидно, что

чение

элемента

максимальное зна-матрицы равно

f ii – 2 f ij + j f

β max = m _i≠ a _j x

_{i i} +f max f_ii – 2min f _ij

^{0 0}          i≠i ₀           i≠ j , _ij ≠f 0

f

ij

m in f ij i≠ j, ij≠f 0

,

где f i0 j0

ma _i x f_ii . Для рассматриваемого

примера

такое максимальное значение равно

Шаг 3. Если элемент матрицы _{∂ U} ( v_i , v_j ) =

= ∞ ( i ≠ j ), то z_ij = 0.

Для рассматриваемого примера нечет кое отношение технологической незави симости ФЭ БС имеет вид

0, 000 0, 990 0,966

0, 000 0, 938

0, 000

-

Z =

0,843 0,860 0, 922 0, 000

0, 926 0,866 0,841

0, 000

0, 000

0,838

0,866

0,841

0,964

0, 000

0, 000

0,979

0,961

0,968

0,929

0,936

0,936

0, 000

0, 983 0,968 0,995 0,932 0,868 0,868

0,978 0, 000

Таким образом, описав задействование ФЭ в ТЦУ АКА нечетким графом производной гиперграфа, можно проводить исследования структурно-техно-

логических, ресурсных,

свойств СУО АКА содержательного и

с

динамических использованием

ратов теории графов [6].

формального аппа-

Так, например, для оценивания степени структурно-технологической живучести отдельно взятого ФЭ БС предлагается использовать значение показателя с ( v.) =

k Σ z j -1 ⁴

, отражающее нормированное kk

Σ Σ z p -1 l -1 ^pl

значение суммарной технологической независимости ФЭ от других ФЭ БС. Тогда для определения уровня структурно-технологической живучести конфигурации СОУ АКА с учетом собственной интенсивности задействования ФЭ в ТЦУ предлагается воспользоваться ^k

5 C ( V )h выражением c - 1-------. При этом вели- max чина fiv равна собственной интенсивности ФЭ СУО, входящего в вершину vi производной нечеткого гиперграфа. Введенный показатель уровня структурно-технологической живучести отражает равномерность интенсивности задействования ФЭ рассматриваемой конфигурации СУО АКА при реализации режимов ориентации заданного ТЦУ на этапе летной эксплуатации. Другими словами, чем равномернее технологически задействуются ФЭ СУО АКА, тем выше показатель уровня структурно-технологической живучести. Используя указанное свойство, могут быть даны рекомендации специалисту по проектированию (управлению) для создания и проведения анализа новых высокоэффективных вариантов структуры СУО (на проектном уровне) или технологии планирования режимов ориентации (на этапе летной эксплуатации), а также совершенствования уже действующих систем. Для рассматриваемого примера f1v = 15,5;

f ₂ ^v = 13,5; f ₃ ^v = 22,5; f ₄ ^v = 18;

f ₅ ^v = 5; f ₆ ^v = 5; f ₇ ^v = 10;

f ₈ ^v = 28,97, а результаты вычисления предложенных показателей равны c ( v ₁) = 0,136; c ( v ₂) = 0,134; c ( v ₃) = 0,139; c ( v ₄) = 0,112; c ( v ₅) = 0,091; c ( v ₆) = 0,109; c ( v ₇) = 0,141; c ( v ₈) = 0,138; C = 0,613.

Проведем анализ изменения уровня структурно-технологической живучести СУО АКА при деструктивных воздействиях на ФЭ СУО. Такие деструктивные воздействия приводят к росту интенсивности задействования неотказавших ФЭ в ТЦУ, а в некоторых случаях — к катастрофическим отказам с потерей полной функциональности системы по другим элементам. Пусть отказ одного из УДМ ({ x ₅, x ₆, x ₇, x ₈}) привел к максимальной интенсивности задействования остальных УДМ при проведении ТЦУ АКА. Граф производной гиперграфа рассматриваемой ситуации представлен на рис. 2.

На рис. 2 вершина v ₃ производной соответствует множеству вершин { x ₅, x ₆, x ₇} нечеткого гиперграфа, при этом f ₁ ^v = 15,5; f ₂ ^v = 13,5; f ₃ ^v = 40; f ₄ ^v = 18; f ₅ ^v = 5; f ₆ ^v = 5; f ₇ ^v = 10; f ₈ ^v = 28,978.

Собственная интенсивность задействования УДМ возросла почти в 1,8 раза. При этом показатели уровня структурнотехнологической живучести рассматриваемой конфигурации примут следующие значения: c(v1) = 0,136; c(v2) = 0,135; c(v3) = 0,135; c(v4) = 0,114; c(v5) = 0,093; c(v6) = 0,111; c(v7) = 0,140; c(v8) = 0,138; C = 0,556. По полученным результатам видно, что снижение уровня структурно-технологической живучести в целом СУО АКА с 0,613 до 0,556 вызвано, с одной стороны, изменением технологической независимости отдельных ФЭ из-за повышения их сов- местного участия в проведении технологических режимов ориентации АКА, а с другой стороны — увеличением интенсивности собственного задействования ФЭ в ТЦУ АКА.

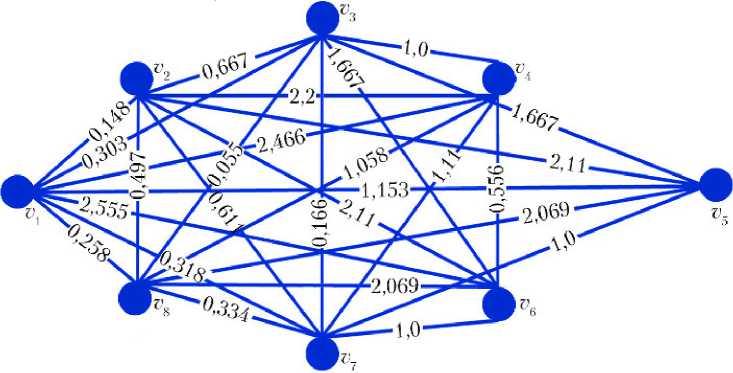
Рис. 2. Граф производной при отказе одного управляющего двигателя-маховика

В случае отказа одного ОЗД и одного ПОЗ собственная интенсивность оставшихся приборов этого типа возрастает в 4 раза ( f ₁ ^v = 15,5; f ₂ ^v = 13,5; f ₃ ^v = 22,5; f ₄ ^v = 18; f ₅ ^v = 20; f ₆ ^v = 20; f ₇ ^v = 10; f ₈ ^v = 28,97). Технологическая независимость принимает следующие значения: c ( v ₁) = 0,135; c ( v ₂) = 0,129; c ( v ₃) = 0,144; c ( v ₄) = 0,104; c ( v ₅) = 0,093; c ( v ₆) = 0,110; c ( v ₇) = 0,141; c ( v ₈) = 0,143. Уровень структурно-технологической живучести СУО АКА снижается всего лишь на 2% и становится равным 0,536.

заключение

В основе предлагаемого в данной работе подхода лежит гиперграфовое формальное представление технологических операций управления АКА. Для оценивания и анализа структурнотехнологической живучести БС АКА предложена операция дифференцирования нечеткого гиперграфа путем построения частотной матрицы интенсивности совместного задействования ФЭ в проведении технологических режимов управления АКА.

При этом, используя производную гиперграфа, можно определить нечеткий граф технологической независимости ФЭ БС, который позволяет ввести показатели уровня структурно-технологической живучести конфигурации БС АКА.

Предложенные показатели можно использовать для оценивания структурнотехнологической живучести БС АКА на этапах проектирования и создания в случае рассматриваемых расчетных, а особенно нерасчетных аварийных полетных ситуаций на борту АКА.

Исследования, выполненные по данной тематике, проводились при частичной финансовой поддержке грантов РФФИ (№ 17-29-07073, 18-07-01272, 18-08-01505, 19–08–00989, 20-08-01046), в рамках бюджетной темы № 0073–2019–0004.