Метод, использующий идеи лагранжевого формализма, для численного моделирования задач упругой динамики

Численно решается задача динамики упругой двумерной среды с неоднородными включениями. Среда считается линейной, при этом ее параметрами являются плотность ρ и упругие константы (параметры) Ламе λ и μ .

Расчетный алгоритм позволяет выполнить эффективную реализацию в смысле соотношения качества решения и времени расчета (включая возможность параллелизма).

Как правило, при математическом моделировании рассматриваемых процессов широко используют методы конечных элементов. Условно теоретические разработки можно разделить на две группы. Первая включает классические методы конечных элементов и их модификации, построенные на прямоугольных сетках. Ярким примером могут служить работы Komatitsch [1], в которых использованы модификации метода Га-леркина. Подобные методы дают хорошие результаты при моделировании распространения упругих волн в однородных средах. В то же время использование указанных методов при описании среды, включающей в себя локальные неоднородные области, затруднено. Вторая группа исследований посвящена изучению методов, позволяющих моделировать среды с разрывными параметрами. Наиболее значимыми здесь являются работы Cocburn, Shu, а также Dumbster [2]. Оба рассмотренных подхода сталкиваются с большими трудностями вычислительного характера при моделировании задач больших порядков аппроксимации по пространству. Хотя частично эти проблемы решаются использованием TVD-методов [3].

Отличие рассматриваемого метода состоит в том, что непрерывная среда заменяется набором дискретных элементов. На каждом элементе дискретизации вводится система аппроксимирующих полиномов, которая описывает смещения точек среды. В результате получается система уравне- ний динамики с конечным числом степеней свободы.

• II.    Пространственная дискретизация

Опишем некоторые технические моменты, необходимые для построения алгоритма.

Введем в рассматриваемой области триангуляцию и будем рассматривать каждый треугольник как дискретный элемент. Вместо рассмотрения смещений каждой точки среды на треугольном полигоне введем функции формы колебаний в виде набора базисных интерполяционных полиномов.

Назовем базисным такой интерполяционный полином, который в одной точке интерполяции принимает значение, равное 1, а во всех остальных точках интерполяции — 0. Например, если точки интерполяции совпадают с вершинами треугольника, тогда базисные интерполяционные полиномы выглядят следующим образом (рис. 1). В данном случае полиномы являются линейными функциями (градиентом серого цвета изображено значение функции).

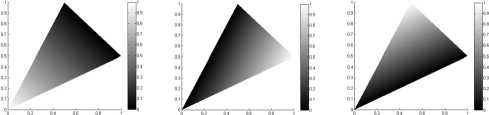
Рис. 1. Базисные интерполяционные полиномы

В общем случае для задания полиномов двух переменных степени k на треугольнике потребуется 2 ( k + 1)( k + 2) точек интерполяции, т. е. требуется расположить внутри треугольника именно такое количество точек интерполяции для того, чтобы по ним однозначно можно было построить любой полином двух переменных степени не выше, чем k .

Будем нумеровать треугольники индексом i,а полиномы в одном треугольнике индексом l, что соответствует базисным функциям Hii (x,y). Причем считается, что функции Hii (x,y) доопределены нулем вне треугольника i. Тогда, например, вектор смещений u(t) можно приблизить линейной комбинацией базисных функций (здесь и далее в формулах подразумевается суммирование по повторяющимся индексам):

un = Hu (x,y) unli (t), (1)

где индекс n нумерует компоненты вектора, а функции u ^nli будем называть степенями свободы.

При таком описании величин они представляются непрерывными функциями в пределах одного треугольника, но эти функции могут терпеть разрыв при переходе от одного треугольника к другому. Потребуем непрерывности величин un . Тогда (1) преобразуется к виду in = Hu (x,y) unli (t) = Hu (x,y) Vpiunp (t), (2) где осуществлен переход от локальной (l,i) нумерации степеней свободы к глобальной p-нумерации.

Требование непрерывности смещений при переходе от одного треугольника к другому налагает ограничения на степени свободы u ^nli , а также на расположение точек интерполяции внутри треугольника. Первое ограничение состоит в совпадении значений u ^nli , принадлежащих разным треугольникам, но относящимся к одной и той же точке на плоскости. Второе — в необходимом количестве точек интерполяции, находящихся на сторонах каждого треугольника. Если брать в качестве интерполяционных точек вершины k ² равных треугольников, полученных при его разбиении (линиями, параллельными сторонам), это ограничение автоматически удовлетворяется.

Переход к глобальной нумерации убирает из рассмотрения повторяющиеся степени свободы, возникающие в первом ограничении (рис. 2). На рисунке изображен переход к глобальной нумерации в случае полиномов первого порядка с точками интерполяции — вершинами треугольников: в каждом из семи треугольников имеется по 3 степени свободы, однако независимыми остаются только 7 из них. Причем каждая относится к своей точке триангуляции.

III. Построение метода

Результаты классической механики для по-

строения численных алгоритмов использовалась ранее. Например, в работе [4] был построен метод, опирающийся на вариационный принцип Лагранжа. Однако рассматриваемый алгоритм существенно отличается от алгоритма в [4].

Выражение для кинетической энергии упругой

среды:

K = — | pU2 dxdy,

D

где p — массовая плотность среды, u — вектор смещений, D — область, в которой происходит распространение волн.

Произведем дискретизацию (3):

К = ¹        nwpw .np

2 u nwpw m np u ,

где m ⁿ _np ^wpw – массовая матрица, индексы n и nw нумеруют компоненты вектора смещений. Способ проведения подобной дискретизации будет описан ниже.

Потенциальная энергия упругой среды записывается в виде [5]:

П =

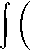
D

^e nwn e    ⁺ 2 ^{A (} e nn ) ^ dxdy,

где λ и μ — упругие константы Ламе,

e nwn

∂u ^nw ∂x n

+

∂u ⁿ ∂x _nw

)

— тензор деформации.

Преобразуем (5), используя приведенное в предыдущей части выражение для вектора смещений:

П =

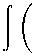
μe _mn

D

e mn

+ 2 A ( enn )2^

dxdy =

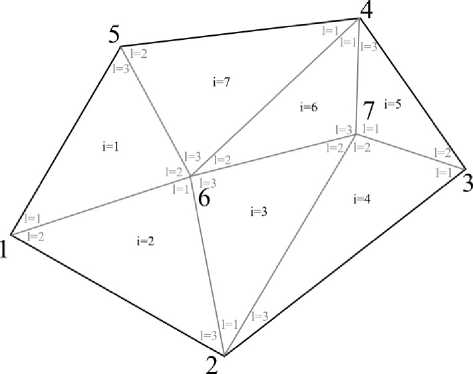
Рис. 2. Переход от локальной нумерации степеней свободы к глобальной

_ ¹        pw pwwlwiw li np

= 2 u nwpw V lwiw P nli     ^V p u ,       W

где P _n ⁿ _l ^w _i ^lwiw — некоторая матрица.

Запишем уравнения Лагранжа для такой (дискретной) системы:

d ∂L      ∂L dt duinwPw   dunwpw

в выражении (7) L = K — П — лагранжиан системы.

Преобразуем производные в уравнениях (7) с учетом выражений (4) и (6):

d ∂L dtdinwpw

d ∂K dtdinwpw

=m

nwpw np np u

∂L ∂u nwpw

pw nwlwiw li np V lwiw P nli     V p u

И окончательно, подставляя (8) и (9) в (7), получаем nwpw np pw nwlwiw li np mnp u = VlwiwPnli Vp u . (1U)

Полученная система обыкновенных дифференциальных уравнений (ОДУ) может быть решена любым стандартным способом. В настоящей работе использовались методы Рунге–Кутта различных порядков аппроксимации.

Исследуем полученную систему ОДУ. Во-первых, так как в уравнениях (7) правые части равны нулю, то эти уравнения автоматически записаны с учетом граничных условий свободной границы. В случае, когда граничные условия отличаются от условий свободной границы, потребуется проанализировать обобщенные силы, возникающие в такой системе из-за наличия подобных связей. Но в любом случае граничные условия в этом методе учитываются уже на этапе построения уравнений и не требуют дополнительного введения.

Во-вторых, данный алгоритм порождает исключительно колебательные решения, то есть в них отсутствуют экспоненциально растущие или затухающие компоненты. Это следует из того, что уравнения Лагранжа, записанные для системы с заданной потенциальной и кинетической энергией, имеют первый интеграл, который называется полной энергией системы. И в данном случае не важно, что при записи этих энергий мы на самом деле воспользовались дискретизацией. Если использовать устойчивые методы решения системы ОДУ, весь алгоритм будет устойчивым.

Будем называть массовой матрицу, которая стоит в качестве множителя перед старшей производной в системе ОДУ. Например, в системе My' = Ay матрица M является массовой матрицей.

В построенной системе (10) массовая матрица m ⁿ _np ^wpw в общем случае не является диагональной. Более того, если бы с кинетической энергией была проведена та же самая операция, что и с потенциальной, массовая матрица получилась бы недиагональной. При рассмотрении случая диагональной массовой матрицы:

к = E 2»npmnp4np = E m"p (2unp)3 ■ (“) np np где mnp = diag(mnWpw).

Выражение (11) может рассматриваться как кинетическая энергия системы материальных точек с массами m _np , которые расположены в точках интерполяции внутри каждого треугольника.

Выбор способа распределения масс может быть различным. Проще всего считать, что угловым точкам приписывается 332 часть массы треугольника, точкам на сторонах — 332 часть, и внутренним точкам — з|2 часть (рис. 3). Каждой точке интерполяции относится по трети площади одного из к2 маленьких треугольников, которые примыкают к ней. Подобное распределение можно трактовать как «стягивание» масс из некоторой окрестности в саму точку. При этом к точкам, к которым примыкает несколько треугольников, стягиваются массы из каждого треугольника.

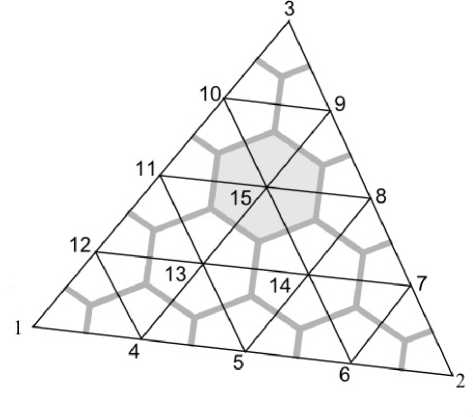
Рис. 3. Пример распределения масс по точкам интерполяции

Например, точке с номером 15 соответствует площадь, примыкающая к ней, выделенная серым цветом. Именно на такой дискретизации кинетической энергии мы и остановились (дискретизация потенциальной энергии (6) остается в силе).

Преимуществом данного подхода является получение системы дифференциальных уравнений, разрешенных относительно старшей производной.

• IV.    Дисперсионный анализ

Для теоретического объяснения некоторых свойств алгоритма (которые также были выявлены при численных экспериментах) удобно воспользоваться методикой дисперсионного анализа. Одна из ее формулировок указана в [6]. При проведении анализа используем известные стандартные подходы. При этом будем выводить дисперсионные соотношения для системы ОДУ, то есть только для дискретизации по пространству.

В силу того, что аналитическое исследование дисперсионных соотношений на неструктурированной сетке в двумерном случае является сложной задачей, исследуем поведение метода на примере одномерного уравнения колебаний струны. Кинетическая и потенциальная энергия имеют вид

K = J РuTdx, — ^ ^      .2

П = J ц ^ 2 dx. — ^

Введем разностную сетку   xp ,   причем hj = |xp — xp+j |. Применим описанный ранее алгоритм к выражениям (12). В этом случае

K = 2 U pw m pw u ^p ,m p^w = 2 p ( h - w + h ^pw ) , p = pw,

∞ n=1 upwPpwuPPpw = P [ H^ ■ Hdx = 2 p p           dx dx

-∞

= P ^<

- ( h - W ) - ¹ , p = pw - 1 ,

(h-W) -1 + (hPw) -1 ,p = pw, - (hPw) -1, p = pw + 1.

Из (13) и (14) получаем уравнения Лагранжа:

P |( h - 1 + h ^pw ) u ^pw = p (( h - w ) ^{- 1} u ^{pw - 1} -

- [(hpw) -1 + (hpw) - 1] uPw + (hpw)-1 uPw+1). (15)

Согласно методике дисперсионного анализа подставим в уравнения (15) u ^p = [ e ^ikx ] ^p и заменим индекс pw индексом p :

P 2( h-1 + hp) up = p ((h-1)—1 e^^h-1 -

• - [( h - 1 ) - ¹ + ( h p ) - 1 ] + ( h p ) - ¹ e i^kh — 1 ) u ^p . (16) Зависимость (16) позволяет вывести закон дисперсии для скоростей распространения волн в дискретной задаче:

-k2c2 = c2 ■ ((h-1)-1 e-ih1 - [(h-1)-1 + (hp)-1 ] +

+ (hp) -1 eikh-1 )/2( h-1 + hp),

где c ² = р — истинная скорость распространения волн.

Разлагая (17) в ряд Тейлора, получаем

~ 2    2^   -JrpP    pPx   ,2 1 ((h-1)3 + (hp)3 )1

c    c V   ik 3(h-1   h 1)   k 12   (h- 1 + hp) J

Или, вводяв (18) обозначения Дh = hp-h,- 1 ,hp = ■ h1p+hp-

и отбрасывая бесконечно малые более высоких порядков, имеем c = c |1+ ik 1дhp

k 2 24( h ^p )²} .     (19)

Полученный результат можно трактовать следующим образом. Член -k224(hp)2 в (19) является «замедляющим» членом. Скорости распространения гармоник уменьшаются с ростом их волнового числа. На картине решения это будет отражаться в появлении за фронтом решения синусоидальных хвостов. Член ik6 Дhp отвечает за рост или убывание гармоник. Как видно, амплитуда изменяется в зависимости от неоднородностей сетки при возрастании или убывании ее шага.

Следует отметить, что подобные выводы верны только в том случае, если начальное возмущение имело форму гармоники. Член, отвечающий за рост гармоник, верен только в начале эволюции. После этого меняется форма решения, в нем появляются другие гармоники. Поэтому наличие члена, изменяющего амплитуду, ещё ничего не говорит о наличии растущих решений, и логических противоречий в том, что он есть, не возникает.

Для метода Галеркина и метода коллокаций дисперсионный анализ демонстрирует такие же результаты с точностью до констант. Знак «замедляющего» члена для метода Галеркина положителен, т. е. гармоники ускоряются, и синусоидальные хвосты появляются перед фронтом решения.

Наконец, стоит ожидать подобного поведения и от построенного метода в случае двумерных уравнений (что и наблюдалось в расчетах).

• V.    Результаты

Разработанный алгоритм был реализован в среде программирования Matlab на одноядерной системе. Метод был протестирован на ряде задач, возникающих из области распространения упругих волн в земле при сейсморазведке.

Рассматривался следующий сценарий. Об- полукруг радиуса 1, 4 Cp

ласть расчета

(C = Xp^P— — скорость распространения продольной волны) с двумя тонкими трещинами (0,1 Cp x 0,02Cp), расположенными под острым углом друг к другу. На диаметре и полуокружности поставлены условия свободной границы. Началь- ное возмущение задано в виде кольца с радиусом 0,08Cp и толщиной 0,03Cp, с центром в центре круга. Сетка состояла из ~ 389 000 треугольни- ков. Использовался метод первого порядка. Время расчета ~ 57 минут.

На рис. 4 изображена картина поля смещений. Хорошо видны отраженные волны от трещин, а также волны Релея, которые возникают в пригра- ничном слое.

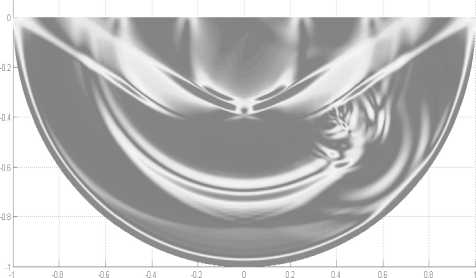
Рис. 4. Картина поля смещений

Сравнительный анализ методов различных порядков. Наиболее интересным для рас- смотренного метода является сравнение его характеристик при использовании полиномов различных степеней внутри одного треугольника. Результаты расчетов на сетке из ~ 25000 треугольников представлены на рис. 5.

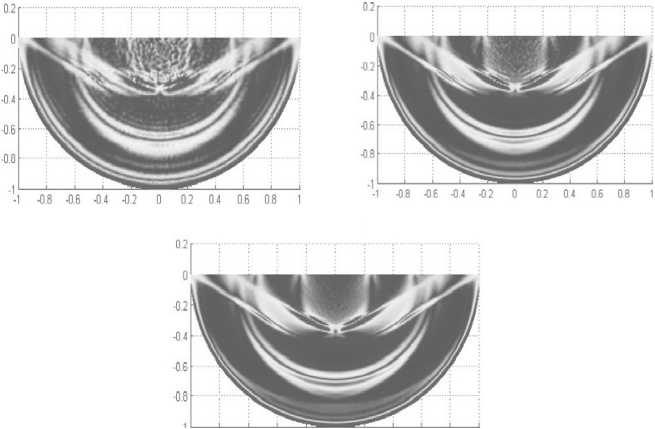
Рис. 5. Сравнение различных порядков аппроксимации по пространству

На рисунке видно улучшение картины при увеличении порядка аппроксимации по пространству. Заметим, что на рисунке, отвечающем расчету с первым порядком аппроксимации, отчетливо просматриваются синусоидальные хвосты за профилем решения. Их появление было предсказано с помощью техники дисперсионного анализа. Можно оценить сложность алгоритма в зависимости от порядка аппроксимации по пространству. Количество степеней свободы пропорционально к ² , где к — порядок аппроксимации по пространству. Количество ненулевых элементов в строках матрицы системы ОДУ пропорционально количеству степеней свободы в одном треугольнике. Если принять, что операции с разреженными матрицами выполняются за время, линейно зависящее от количества ненулевых элементов, то получаем зависимость общего время решения задачи от порядка аппроксимации по пространству как к 4 . На практике временные затраты на проведение расчетов, указанных на рис. 5, составляют 56, 743 и 3858 секунд соответственно. Эти результаты находятся в хорошем соответствии с теоретическим анализом.

Для исследования сеточной сходимости метода было выполнено сравнение решения на различных сетках. Для этого использовался следующий подход.

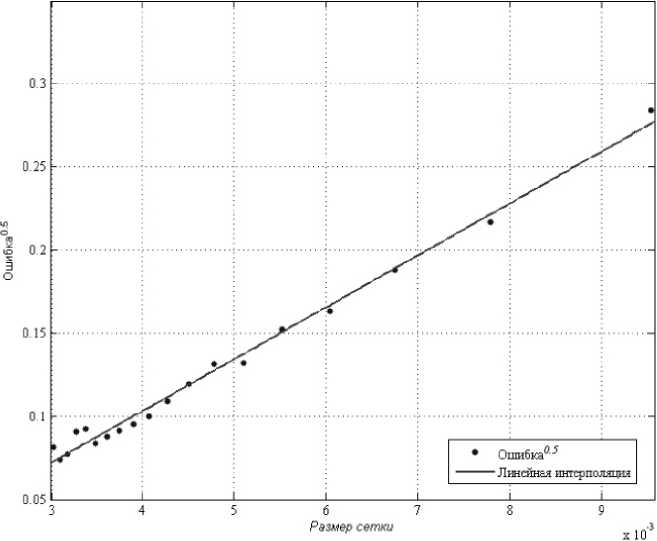
Рис. 6. Исследование сеточной сходимости

В области случайным образом выбиралось большое число точек. В этих точках вычислялись значения решений на финальном временном слое. Эти данные и подлежали дальнейшему анализу. В качестве точного использовалось решение на самой подробной сетке.

Результаты для метода первого порядка представлены на рис. 6. Данный график демонстрирует зависимость корня из ошибки от размера сетки. Поскольку использовался метод первого порядка, то ошибка должна быть квадратичной по размеру сетки. Самым точным расчетом был расчет на сетке с размером треугольника 0 , 001.

• VI.    Выводы

Рассматриваемый метод позволяет проводить расчеты больших задач упругой динамики (характерные размеры сеток — 10 ⁶ треугольников) за небольшие промежутки времени (характерные времена 2--3 часа при расчетах на времена распространения волн в области, размер которой составляет порядка 1 , 4 C p ) даже при реализации на одноядерной системе. При этом метод принципиально допускает возможность эффективного распараллеливания. Устойчивость метода гарантируется получением системы ОДУ, разрешенной относительно старшей производной, матрица которой имеет чисто мнимые собственные значения (и ее последующего решения устойчивым методом). Проведенные исследования сеточной сходимости и зависимости времени работы от порядка аппроксимации по пространству не противоречат известным теоретическим соотношениям и приведенным оценкам. Метод допускает рассмотрение сред с переменной плотностью и жесткостью.

Работа выполнена при поддержке министерства образования и науки Российской Федерации (конкурс № НК-571П в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009--2013 годы). А также федерального агентства по науке и инновациям (лот «Проведение научных исследований коллективами научно-образовательных центров в области механики», шифр заявки «2010-1.1-112-024-046» в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009--2013 годы).