Метод исследования термофлуктуационных процессов в задачах диагностики и прогнозирования изоляционных материалов

Введение. Увеличение перетока электроэнергии в энергосистемах приводит к тому, что СКЛ используют на пределе их физических возможностей, следствием чего является пробой электрической изоляции [1]. Таким образом, вопросы обеспечения энергетической безопасности, а также повышения эффективности передачи электроэнергии выходят на первый план.

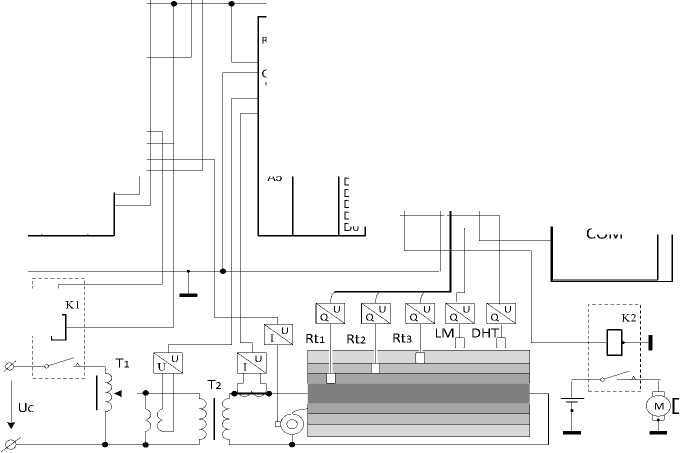
Важной характеристикой СКЛ является нагрузочная способность, определяемая тепловым режимом. По ней рассчитывается площадь поперечного сечения и пропускная способность СКЛ [2]. Ресурс изоляционных материалов зависит от таких параметров, как температура, ток, влажность [3]. СКЛ с изоляцией из сшитого полиэтилена (СПЭ) обладает высокими термоизолирующими свойствами. Поэтому пропускная способность и надежность в значительной степени зависят от температурного режима работы. Для решения указанной проблемы используется мониторинг температуры кабеля во время работы. Для исследования температурного поля в сечении СКЛ используется цифровой регистратор (рис. 1).

220 Om

220 Om

220 Om

LSD 1602

VSSVDDVORSRWED1D2D3D4D5D6D7

D9

D8

D7

D6

D5

D4

D3

D2

D1

D0

RESET

RESET

D13

D13

D12

D12

D11

D11

D10

D10

A3

A3

A4

A4

A5

COM

5V GND

VIN A0

A1

A2

5V GND VIN A0

A1

A2

Arduino Uno

Arduino Uno

D9

D8

D7

D6

D5

D4

D3

D2

D1

D0

A5

Рис. 1. Схема цифрового регистратора для проведения экспериментальных исследований

Fig. 1. Diagram of digital recorder for conducting experimental studies

Современные средства мониторинга распределенной по длине линии температуры не имеют подходящих для этого моделей и алгоритмов расчета тепловых процессов в изоляции кабеля [4].

Представленное исследование термофлуктуационных процессов основывается на методе регистрации температуры внутри изоляции. Распределенные оптоволоконные системы с установленными в пределах поперечного сечения СКЛ волоконнооптическими датчиками измеряют внутренние температуры для определения точек повышенного нагрева. Для исследования законов передачи температуры в лабораторных условиях решено применить послойное размещение датчиков (рис. 1).

При появлении частичного разряда (ЧР) в изоляционном материале рассеивается энергия, основная часть которой затрачивается на деструкцию изоляционного материала. Поэтому в месте действия ЧР осуществляется нагрев изоляции, что и является объектом измерения [5, 6]. Учитывая общие требования к системам измерения термофлуктуационных процессов и проблематику измерения, следует отметить, что существующие цифровые регистраторы не позволяют одновременно реализовать необходимый набор диагностических функций. Поэтому была использована система цифровой регистрации термофлуктуационных процессов, разработанная на кафедре электротехники и мехатроники (ЭиМ) Южного федерального университета (ЮФУ) [5].

Разработка алгоритма и системы мониторинга тепловых процессов СКЛ. Разработанная система измерения термофлуктуационных процессов сочетает в себе все достоинства современных цифровых измерительных систем, а именно:

• —    мониторинг тепловых процессов с помощью системы SCADA , реализованной в среде LabVIEW ;

• —    мониторинг в режиме реального времени послойного измерения температуры;

— регулирование и измерение влажности и т. д. (рис. 1 [5]).

Исследование повышенного перегрева термофлуктуационным методом предусматривает использование в лабораторных экспериментах температурных датчиков, расположенных послойно в СКЛ (см. рис. 1), для создания моделей и алгоритмов расчета тепловых процессов в изоляции.

Таким образом, разработанная схема автоматизированной системы контроля состояния изоляции SMaCTC : — позволяет независимо или совместно использовать два метода контроля (прогнозирования развивающегося дефекта изоляции и неразрушающего контроля термофлуктуационных процессов);

• —    имеет набор диагностических функций по контролю режимов работы СКЛ (номинальной нагрузки, холостого хода, короткого замыкания) по результатам полученного профиля температур, снятых датчиками [5, 6].

Алгоритм работы программного обеспечения цифрового регистратора контроля параметров СКЛ представлен на рис. 2.

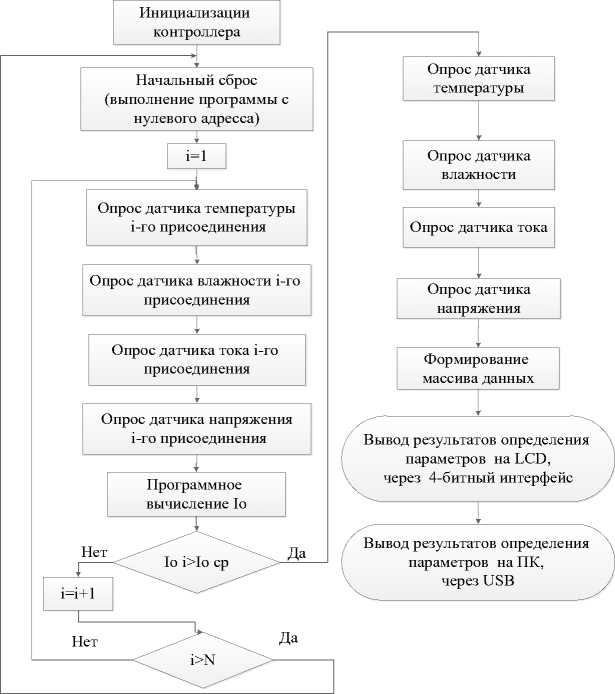
Рис. 2. Алгоритм функционирования регистратора контроля параметров СКЛ

Fig. 2. Algorithm of PCL parameters monitoring recorder operation

Машиностроение и машиноведение

Таким образом, обобщенный алгоритм:

• —    во-первых, позволяет управлять процессом диагностики параметров СКЛ;

— во-вторых, эффективно реализует метод контроля термофлуктуационных процессов в изоляционных материалах СКЛ посредством цифрового регистратора.

Моделирование термопроцессов изоляции СКЛ с использованием пакета LabVIEW . Для исследования термофлуктуационных процессов в СКЛ создан виртуальный инструмент LabVIEW , который:

• —    позволяет взаимодействовать с измерительными датчиками и управляющей аппаратурой;

• —    осуществляет сбор, обработку, отображение информации и результатов расчета;

• —    моделирует как отдельные объекты, так и цифровую систему SMaCTC в целом.

Вид панели виртуального инструмента представлен на рис. 3.

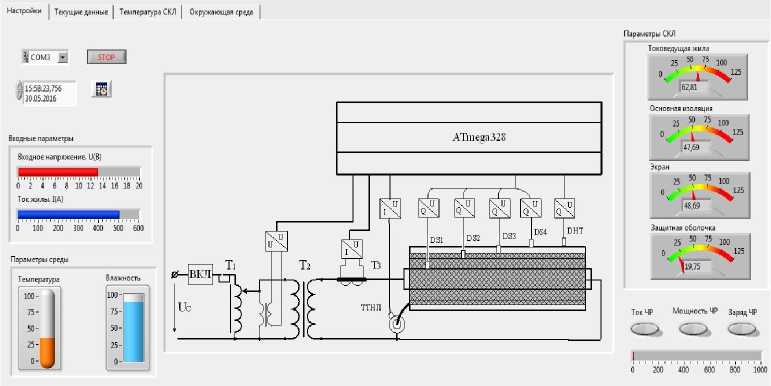
Рис. 3. Панель виртуального инструмента LabVIEW

Fig. 3. Virtual toolbar LabVIEW

Стенд для исследования термофлуктуационных процессов представляет собой компьютерную модель LabVIEW на рабочем столе персонального компьютера и содержит модели виртуального инструмента: — данные и графики температур;

• —    данные и зависимости влажности;

• —    анализ и средние данные температур;

• —    временную зависимость тока [6].

Программное обеспечение позволяет рассчитывать значения тока, напряжения, температуры жилы кабеля, влажности, тока нулевой последовательности (I _ТНП ) с интервалом времени 1 с.

Таким образом, создана автоматизированная система контроля характеристик изоляционных материалов SMaCTC , позволяющая контролировать термофлуктуационные процессы СКЛ напряжением 10 кВ. При этом используется метод неразрушающего контроля термофлуктуационных процессов в изоляционных материалах СКЛ. Специальное программное обеспечение снимает информацию о работе SMaCTC .

Мониторинг тепловых условий кабеля и окружающей среды. Для исследования тепловых режимов СКЛ использовались математические и имитационные модели силового кабеля с СПЭ [6, 7, 8, 9]. В этом случае кабель и окружающая среда разбиваются на зоны, представленные в виде электрической схемы замещения (рис. 4).

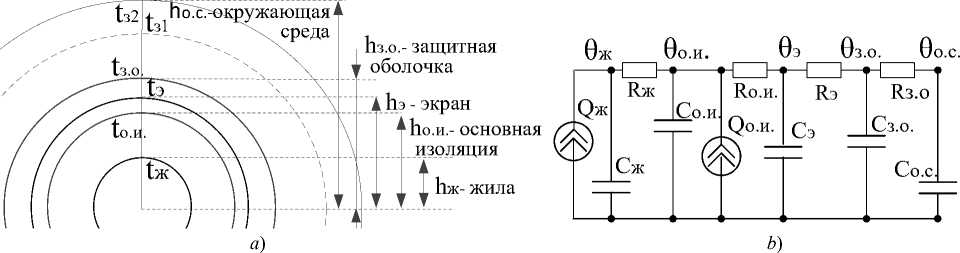
Рис. 4. Сечение кабеля ( а ) и его эквивалентная тепловая схема замещения ( b )

Fig. 4. Cable cross-section (a) and its equivalent thermal replacement circuit (b)

Здесь θ ж , θ э , θ о.и. , θ з.о. , θ о.с. — соответственно температуры на жиле, экране, основной изоляции, защитной оболочке, окружающей среде; C ж , C э , C о.и. , C з.о. , C о.с. — теплоемкости соответственно жилы, экрана, основной изоляции, защитной оболочки, окружающей среды; R ж , R э , R о.и. , R з.о. — тепловые сопротивления соответственно жилы, экрана, основной изоляции, защитной оболочки; Q ж , Q о.и — источники тока, замещающие температурный напор, создаваемый током, протекающим по жиле и экрану.

На рис. 4 показаны слои и точки, в которых проводится контроль тепловых параметров. Исследование распределения температуры кабельной линии выполнялось в соответствии с теорией теплопроводности, при этом использовалось дифференциальное уравнение Фурье [10].

Физические свойства материалов и геометрические размеры элементов кабеля АПвПу г-1х30/25-10 [5, 6] сведены в табл. 1 [11].

Таблица 1

Table 1

Параметры кабеля

Cable parameters

Материал Параметр	Алюминий	СПЭ	Медь	Воздух
Удельная теплопроводность, Вт/(м·К)	209,3	0,38	400	0,024
Плотность, кг/м 3	2700	2200	8700	1,2
Удельная теплоемкость, Дж/(кг·К)	920	1900	385	1005

Профиль температур в сечении силового кабеля (рис. 4) определялся системой уравнений в соответствии с теорией теплопроводности.

⎧        θ ο.c +( ж ₊- ^э )⁄2π ϰ,(ℎ=ℎ )

ο.c       ж ж     Y _{э э}                        о․с․

⎪^θ(ℎ о․с․ ^{) +} lit ( о․с․ ) ( 7 ж ₊ 7           o.c , з․о․            о․с․

⎪                    x / xy ж ж Y э э

⎪ θ(ℎз․о․) + In( з․о․)(7ж+7          о․и․, э           з․о․ x n / xyж ж   Уэ э r2

ж э h^^TV            1.7.X

⎪ θ(ℎ э ) + In ⁽7 э ) ^{5 ж 1 ж} 2n. э _{э      +} э ( э 7 э ⁾ , (ℎ о․и․ ≤ℎ≤ℎ э )

^⎪     θ⁽ℎ о․и․ ⁾ + In ( о․и․ ) 7 ^ж ⁄2πλ о․и․ , (ℎ ж ≤ ℎ≤ ℎ о․и․ )

X / у ж ж

⎩     θ(ℎ ж ) + δ ж (ℎ ж -ℎ²)⁄4λ ж γ ж , (0 ≤ ℎ ≤ ℎ ж )․

Здесь λ_о․с․, λ_о․и․, λ_э, λ_ж, — удельные теплопроводности окружающей среды, полиэтилена, экрана и жилы соответственно; I ж , I _э — токи на жиле и экране; ϰ — коэффициент теплопроводности; δ_ж = I ж ⁄ s _ж; δ_э = I э ⁄ s э ; s ж , s э — площади поперечного сечения жилы и экрана; γ_ж, γ_э — электропроводности жилы и экран.

В соответствии с системой уравнений (1) в MatLab строится профиль температур в сечении кабеля и окружающей среды [6, 12].

Сравнительный анализ экспериментальных и расчетных характеристик распределений температуры. Для доказательства адекватности предлагаемой упрощенной математической модели СКЛ авторы провели исследования, в ходе которых через кабель пропускался переменный ток, величина которого изменялась в зависимости от режима работы (рис. 5).

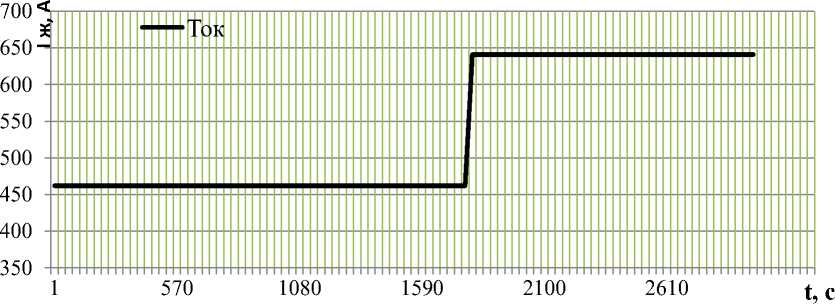
Рис. 5. Экспериментальная диаграмма тока в кабеле

Fig. 5. Experimental diagram of current in cable

Машиностроение и машиноведение

В ряде работ [1, 6, 13] представлены модели, с помощью которых рассчитывается распределение температуры по слоям, а также зависимость, позволяющая определять температуру жилы (0ж, °С).

Предлагается упрощенная аналитическая зависимость (2) определения температуры наиболее нагретой точки изоляции (жилы кабеля), полученная из системы (1). Температура жилы кабеля вычисляется с учетом температуры поверхности кабеля, окружающей среды и тока жилы:

∙   ∙      ∙   ∙    ·     [       ∙( доп о.с.( ))]

⁰ Ж⁽^ ) = ⁰ З.О.⁽^ ) ⁺                  _s                  ■

В опытах использовался силовой кабель АПв Пу г-1х30/25-10.

Здесь 0_ж — расчетная температура жилы кабеля, °С; 0 _з._о. = 23 °С — измеренная температура поверхности кабеля (защитная оболочка); п = 1 — число жил кабеля; I — максимальный ток кабеля при проведении измерений, А; р₂₀= 2,8^10^-8 Ом^м — удельное электрическое сопротивление жилы кабеля при 20 °С; Т_к = 0,0028 °С, м/Вт — сумма термических сопротивлений изоляции и защитных покровов кабеля; m — экспериментальный множитель; К _р = 1,02 — поправочный коэффициент для приведения электрического сопротивления к расчетной температуре; а = 0,0043081 °С

— температурный коэффициент сопротивления материала жилы [7]; 0доп = 90 °С — длительно допустимая температу ра изоляции жилы; 0о.с. = 23 °С — измеренная температура окружающей среды; S = 0,003 8465 — сечение жилы кабеля, м2.

Итак,

1∙   ∙2,8∙10   ∙ 0,0028 ∙ 1,02[1 + 0,004308 ∙ (90 - θ ο.c. ( ))]

^{θ ж ( ) = θ ɜ.ο. ( )+}                          3,8465 ∙ 10                           ^․

Основное назначение уравнения (2) — рассчитать температуру жилы кабеля максимально просто. Уравнение учитывает лишь стационарные тепловые процессы в кабеле и справедливо при установившихся значениях измеряемых величин. Это характерно и для всех нормативных документов по расчету тепловых процессов в силовых кабелях: МЭК (1ЕС) 60287, ГОСТ Р МЭК 60287-1-1, ГОСТ Р МЭК 60287-1-2, ГОСТ Р МЭК 60287-1-3, ГОСТ Р МЭК 60287-2-1, ГОСТ Р МЭК 60287-2-2.

При эксплуатации вполне естественно, что измеряемые величины изменяются во времени, таким образом, для их учета необходимо вести расчет нестационарных тепловых процессов.

Эксперимент 1 . Экспериментальная диаграмма ступенчатого изменения действующего значения тока кабеля приведена на рис. 5. Экспериментальные и расчетные временные зависимости процесса нагрева кабеля, выражение (2), построенные при ступенчатом изменении тока, приведены на рис. 6.

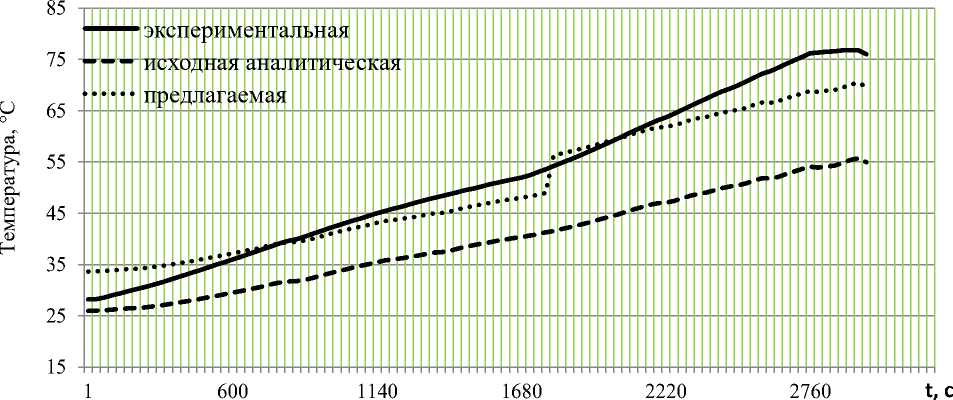
Рис. 6. Экспериментальные и расчетные временные зависимости процесса нагрева кабеля

Fig.6. Experimental and calculated time dependences of cable heating process

В результате экспериментальных исследований получены показатели качества предложенной математической модели тепловых процессов силового кабеля:

• —    относительная погрешность модели не превышает 11 %;

• —    среднеквадратическое отклонение экспериментальных данных от расчетных по модели не превышает 4,5 ^оС.

Не учтено влияние теплообмена через торцы исследуемого кабеля в исходной модели. Во время проведения эксперимента торцы жилы не были закрыты теплоизолирующей тканью, и происходил теплообмен с держателями.

Из-за малой длины образца этот теплообмен оказал влияние на результат. Приведенные диаграммы демонстрируют корреляцию экспериментальных и расчетных кривых температуры, что говорит о верном выборе математической модели [2, 4].

Эксперимент 2 . Для проверки адекватности разработанной математической модели на основе мощного понижающего трансформатора с выходным током до 640 А была создана измерительная система (рис. 1), позволяющая исследовать тепловые процессы в одножильных кабелях. Датчики температуры послойно размещались внутри и на поверхности СКЛ, а также на некотором удалении от него. Значение тока определялось посредством измерительного трансформатора. Все измерения проводились с помощью цифрового регистратора, подключенного к компьютеру. В качестве образца использовались отрезки заведомо исправных кабелей с изоляцией из сшитого полиэтилена АПв Пу г-1х30/25-10 длиной 0,85 м. Экспериментальная диаграмма действующего значения тока приведена на рис. 7.

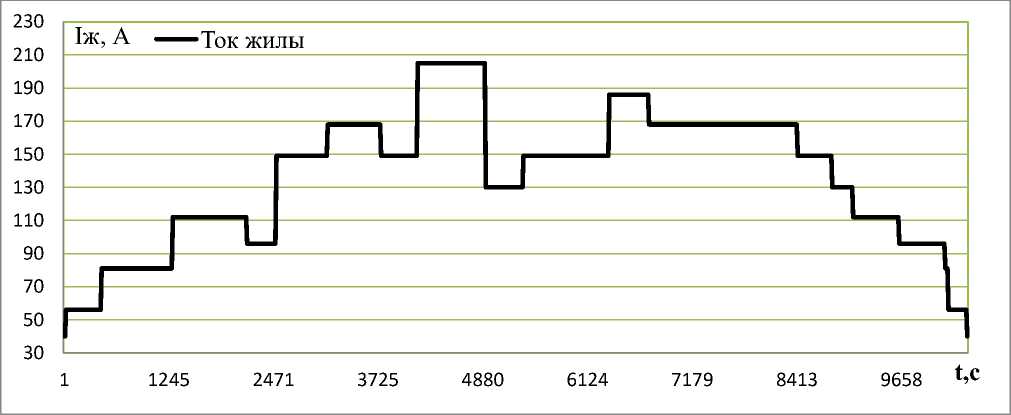
Рис. 7. Экспериментальная зависимость для действующего тока СКЛ

Fig. 7. Experimental dependence for PCL rms current

На рис. 8 приведены экспериментальные и расчетные временные диаграммы температуры кабеля АПв Пу г-1х30/25-10 по опыту, представленному в рис. 7.

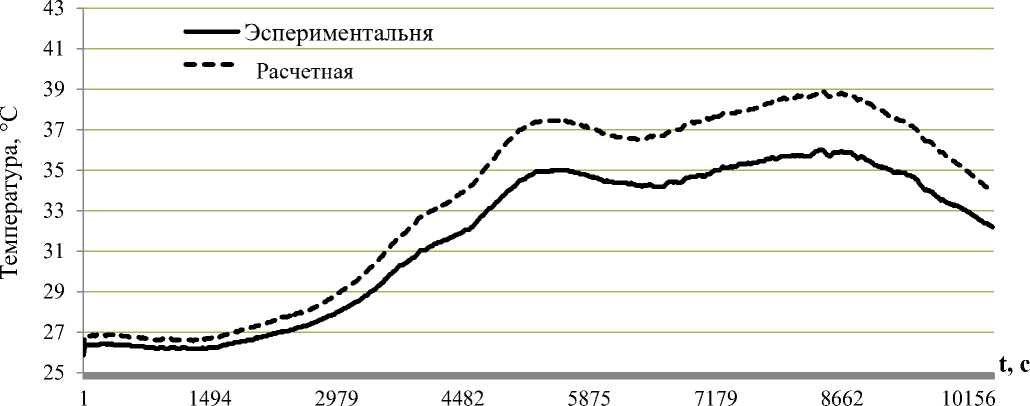
Рис.8. Временные диаграммы температуры на жиле кабеля АПв Пу г-1х30/25-10

Fig.8. Temperature time diagrams at cable core APv Pu g-1x30 / 25-10

Расчет показателей качества тепловой модели СКЛ. Введем показатели качества тепловой модели для анализа и оценки погрешностей расчета температуры по рассматриваемым тепловым моделям [14].

Пусть (Д0)₇- — абсолютная погрешность расчета температуры жилы на интервале расчета (или измерения) j .

То есть

Машиностроение и машиноведение

(Δθ) = (θp) -(θэ) , где j — номер интервала расчета.

В качестве показателя качества будем рассматривать величину

Δθ ΜАКС =     {|(Δθ) |}.

Погрешность ΔθΜАКС характеризует диапазон точности тепловой модели, то есть границы, в которых могут находиться значения величин (Δθж) .

Рассмотрим также средние значения векторов (Δθи) и (Δθp) как показатель качества тепловой модели:

Δθ̅ p =

∑   [(Δθ p )]

,

Δθ^̅ э

и

∑    [(∆ э) ]

=,

где n — количество интервалов на расчетном промежутке времени.

Величины Δθ р и Δθ э характеризуют ошибки расчета температуры жилы в статике, то есть по постоянной составляющей. Для анализа качества тепловой модели в динамике будем рассчитывать коэффициент корреляции:

∑  [(θ p ()-θ̅ p )-(θ э ()-θ̅ э )]

√∑  [θ p ()-θ̅ p ] ∙∑  [θ э ()-θ̅ э ]

где

Δθ̅ p =

∑    р()

п

, Δθ̅ э

∑    э()

.

и

Обсуждение и заключения. Результаты расчета показателей качества математической модели по эксперименту 1, полученные путем сравнения измеренной и расчетной температуры кабеля, приведены в табл. 2.

Таблица 2

Table 2

Показатели качества тепловой модели при ступенчатом изменении тока

Thermal model quality parameters under stepwise current variation

Показатели точности расчета Значения погрешности по формуле стандартной предлагаемой Диапазон точности ΔθМАКС 22,419 7,657 Показатель качества (среднее значение векторов) 12,114 1,559 Коэффициент корреляции 0,822 0,988 Максимальная относительная погрешность, % 29 10 Среднеквадратическое отклонение 14,96 12,29

Полученные высокие значения коэффициента корреляции свидетельствуют о соответствии математической модели реальным тепловым процессам. Максимальная абсолютная погрешность при сравнении экспериментальных данных и расчетов по исходной формуле (рис. 6) составила 22,4 °С. Максимальная абсолютная погрешность при сравнении экспериментальных данных и расчетов по предлагаемой формуле (рис. 6) составила 7,6 °С.

Результаты расчета показателей качества математической модели по эксперименту 2, полученные путем сравнения измеренной и расчетной температуры кабеля, приведены в табл. 3.

Таблица 3

Table 3

Значения показателей качества тепловой модели

Thermal model quality parameters values

№ пп.	Показатели точности расчета	Погрешность по результатам расчета
1	Диапазон точности Δ θ МАКС	2,9
2	Среднее значение векторов	1,8
3	Коэффициент корреляции	0,999
4	Максимальная относительная погрешность, %	5,4

Максимальная абсолютная погрешность расчета температуры по отношению к непосредственно измеренной температуре не превысила 2,9 °С. Высокие значения коэффициента корреляции свидетельствуют о соответствии математической модели реальным тепловым процессам.

Предложенная аналитическая зависимость может применяться в качестве базовой при вычислении тепловых процессов СКЛ в режиме реального времени, так как ее адекватность подкреплена опытными данными.

Выводы. Исследования показали, что разработанные расчетные соотношения даже в условиях принятых упрощений достаточно корректно описывают тепловые процессы в кабеле. Применение рассмотренных устройств повысит эксплуатационную надежность систем электроснабжения. Основная область применения разработанной математической модели — диагностика и прогнозирование ресурса изоляции силового кабеля. Цифровое аппаратное устройство способно измерять температуры поверхности кабеля и окружающей среды, а затем в режиме реального времени рассчитывать внутренние температуры и решать задачи раннего выявления повреждений.

Работа выполнена по гранту № ВнГр-07/2017-15 «Разработка теоретических основ и методов построения интеллектуальных многосвязных систем управления процессами производства, транспортировки, распределения и потребления энергии».