Метод измерения характеристик периодических сигналов, инвариантный к погрешностям формирования дополнительного сигнала

Δα [4]. Однако при отличии углов сдвига фаз в каналах напряжения и тока возникает дополнительная погрешность. Реализация методов, использующих формирование только дополнительного сигнала напряжения, может привести к возникновению погрешности по напряжению (погрешности по модулю) ФСБ, обусловленной отличием амплитуд входного и дополнительного сигналов [5].

В [6] авторами разработан метод, который обеспечивает повышение точности измерения ИХГС за счет исключения данного вида погрешности. Однако реализация метода предусматривает проведение дополнительных измерений мгновенных значений как входного, так и дополнительного сигналов с целью определения корректирующего коэффициента, что увеличивает время определения параметров и аппаратурные затраты. В статье рассматривается новый метод, не требующий специальной коррекции мгновенных значений сигналов и инвариантный к погрешностям формирования дополнительного сигнала.

Метод измерения интегральных характеристик на основе сравнения мгновенных значений гармонических сигналов, разделенных в пространстве. Разработанный авторами метод измерения ИХГС основан на формировании двух дополнительных сигналов напряжения: первого – инверсного входному и второго – сдвинутого относительно входного на произвольный угол Δα. Метод заключается в том, что в момент равенства дополнительного сигнала напряжения, сдвинутого по фазе относительно входного на угол Δα, и сигнала, инверсного входному, измеряют первые мгновенные значения входного напряжения и тока; в момент равенства дополнительного и входного напряжений измеряют вторые мгновенные значения входных сигналов напряжения и тока. ИХГС определяют по измеренным значениям. Временные диаграммы, поясняющие метод, представлены на рис. 1.

В момент времени t 2 , когда U ₁₂ = U ₃₂, мгновенные значения сигналов примут вид:

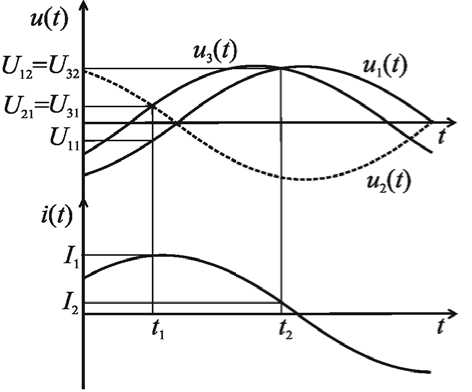
Рис. 1. Временные диаграммы, поясняющие метод

U12 = Um Sin a2 • U32 = Um Sin(a2 + Aa) • ;;

12 = Im Sin(a2 +Ф)

где a ₂ - начальная фаза входного напряжения в момент времени t ₂ .

Равенство мгновенных значений сигналов

U ₁₂ = U ₃₂ выполняется

a 2 = a 2 + Aa,

Aa = n + 2n l — 2a 2

тт д-тт Aa

^U 12 =± Um ^cos^" и

то

или

в том случае, если есть, когда

_ 3nl Aa a 2 = “2---2"". Отсюда,

¹ 2 = ± I m ^cos l Ф

—

Aa

.

Используя мгновенные значения сигналов, после преобразований получим выражения для определения ИХГС:

- СКЗ напряжения и тока

Если входные напряжение и ток имеют гармонические модели: u 1 ( t ) = U m sinro t ; i ( t ) = I_m sin ( ro t + ф ) , то дополнительные напряжения примут вид: и 2 ( t ) = - U_m sin ro t и и 3 ( t ) = U m sin ( ro t + Aa ) , где U m и I_m — ампли-

^U СКЗ =

I СКЗ =

U 11 ^{+ U} 12

;

¹ 1 ^{+ 1} 2

;

- активная и реактивная мощности

тудные значения напряжения и тока; ω – угловая частота входного сигнала; φ – угол сдвига фаз между входными напряжением и током.

В момент времени t i , когда U ₂₁ = U ₃₁ , мгновенные значения сигналов примут вид:

^U 11 = ^Um ^{Sin a} i

;

^U 21 = ^— U m ^{Sin a} 1 U 31 = ^Um ^{Sin (a} 1 ^{+ Aa)}- ;;

11 = Im Sin(a1 +Ф)

,

p = I 2 | ^U 12 |    1 1 | ^U 111

;

Q =

¹ 1 | ^U 12 ^{+ 1} 2 | ^U 111

Информационно-измерительная система (ИИС), реализующая метод представлена на рис. 2.

где a 1 - начальная фаза входного напряжения в

момент времени t 1 .

Равенство мгновенных значений сигналов

U 21 = U ₃₁ выполняется в том случае, если

a1 = a1 + Aa

Aa = 2nl — 2a1

сюда, при l =0

(Aa* 0), то есть, когда , Aa или a1 = пl — “2“, где l=0, 1. От- тт         I Aa)

^{U 11} U m   ^ 2 J , а при l =1

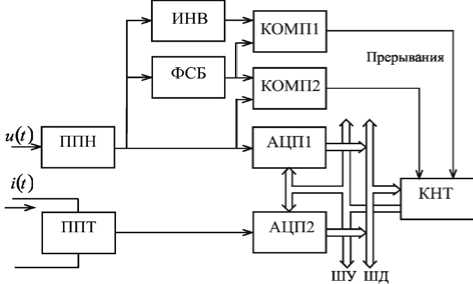
Рис. 2. Схема ИИС, реализующей метод

Aa

^U 11 = U m ^Sin —

Aa

, то есть U 11 ± U m ^Sin 2 . В этом

случае

I Aa

I 1 = I m ^Sin l ^{П l} + Ф 2"

или

¹ 1 = ± I m ^Si n| Ф^-

Aa)

T J.

В состав ИИС входят: первичные преобразователи напряжения ППН и тока ППТ, аналогоцифровые преобразователи АЦП1 и АЦП2, компараторы КОМП1 и КОМП2, фазосдвигающий

блок ФСБ, осуществляющий сдвиг входного напряжения на угол Да , инвертор ИНВ, контроллер КНТ, шины управления ШУ и данных ШД. Анализ показывает, что в случае наличия погрешности по модулю ФСБ дополнительный сигнал напряжения примет вид

u3 (t ) = Um3 sin (to t + Да) , где U m3 - амплитудное значение напряжения на выходе фазосдвигающего блока.

В этом случае равенство мгновенных значений сигналов напряжения произойдет в моменты времени t i и t 2

U 21 = U 31 = U m з sin ^(a ‘ + ^Да) и ^U 12 ^{- U} 32 ^- U m 3 ^{sin (a} 2 ^{+ Да)}

.

Поскольку изначально считалось, угол сдвига Δα – произвольный, то это не приведет к погрешности, а сместит моменты равенства сигналов. Таким образом, метод и реализующая его ИИС инвариантны к погрешностям формирования дополнительного сигнала. Предлагаемый метод предназначен для измерения интегральных характеристик сигналов с гармоническими моделями. При наличии в сигналах высших гармоник неизбежно возникает погрешность.

Анализ погрешности метода из-за отклонения реального сигнала от гармонической модели. Для анализа методической погрешности, обусловленной отклонением реального сигнала от гармонической модели, используем методику оценки погрешности результата измерения интегральной характеристики как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению модели от реального сигнала. Погрешность вычисления значения какой-либо функции, аргументы которой заданы приближенно, может быть оценена с помощью дифференциала этой функции [1]. Если абсолютные погрешности аргументов соответствуют наибольшему отклонению моделей от реальных сигналов, то предельные значения абсолютных погрешностей определения характеристик сигналов в соответствии с (1) – (4) примут вид:

\

^Д U СКЗ ^{- ( u} СКЗ ) U 11 ^{+ (} U СКЗ )

U ₁₂

^Д U max

;

^{Д /} СКЗ ^{- (} I СКЗ ) 1 1 ^{+ (} I СКЗ ) I 2 ^{Д /} 1

max

;

Д Р - ( Р ) 1 1 + ( Р ) 1 2 Д / max

+ ( Р ) U 11 + ( Р ) U 12

Д U _тах

;

^{Д U} max

где Д Umax, Д/max - предельные абсолютные погрешности аргументов, соответствующие наибольшим отклонениям моделей от реальных сигналов.

В общем случае предельные абсолютные погрешности, соответствующие наибольшим отклонениям моделей от реальных сигналов имеют вид:

тока и приведенные погрешности измерения АМ и РМ:

ОТ                                    ОТ

Д Umax = U1 m £ huk  Дmax = 11 m 2 h/k k=2     и               k=2

^u

U СКЗ

ОТ

2 h uk

_ k - 2

+

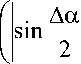
Да cos

ОТ

1 + 2 h uk k - 2

где h uk ^- U km

U 1 m

и h ik - y m - коэффициенты k -тых I 1 m

гармоник напряжения и тока; U _{1 m} и I _{1 m} - ампли-

туды первых гармоник сигналов; U _km и I_km - амплитуды k -тых гармоник напряжения и тока. Используя (1)-(8), можно определить относительные погрешности измерения СКЗ напряжения и

5/

I СКЗ

ОТ

2 hik k-2

sin I ф

Да

+ cosI ф

ОТ

1 + 2 h^k k - 2

;

Да

те

Да

Z h uk sin 2 ⁺

Y p = Y q =

k = 2     V

те i+zh2

uk к=

<

Z hik sink + k = 2    L V

—

Да

+ cosl ф

Да cos

те

1+Z hk k=2

ДаУ

—

Полученные результаты позволяют выбирать области использования метода в зависимости от спектра сигналов и требований по точности измерения, а также подбирать оптимальные параметры измерительного процесса для обеспечения наименьшей погрешности.

те                  те

1+ Z    1 + Z h k

к = 2

к = 2

.

На рис. 3 представлен график зависимости относительной погрешности измерения СКЗ напряжения от Да в соответствии с (9) при наличие в сигнале первой и третьей гармоник с h u з = 1% .

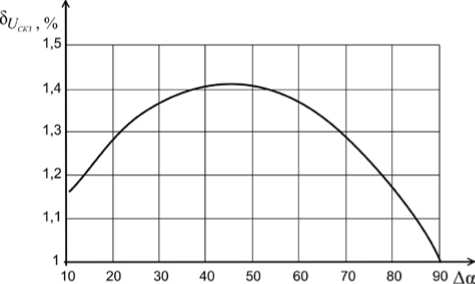
Рис. 3. График зависимости δ U от Δα

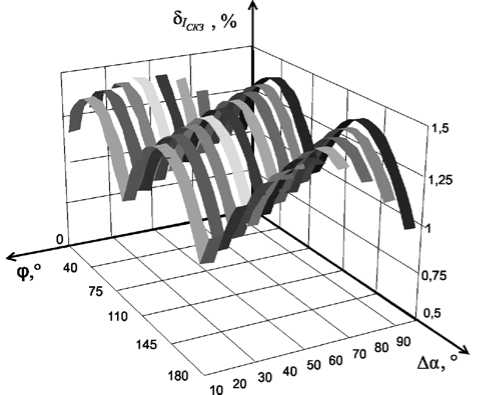
Рис. 4. Графики зависимости δ I от Δα и φ

На рис. 4 и 5 представлены графики зависимости погрешности измерения СКЗ тока, АМ и РМ от ^Да и ф согласно (10) и (11) при наличие в сигнале первой и третьей гармоник с h u з = hi з = ¹ % .

Анализ выражений (9)-(11) и рис. 3-5 показывает, что погрешности измерения ИХГС из-за отклонения реального сигнала от гармонической модели зависят от спектра сигнала и угла сдвига фазы ФСБ. Кроме того, погрешности измерения СКЗ тока, АМ и РМ зависят также и от угла сдвига фаз между первыми гармониками напряжения и тока.

Выводы: разработанный метод измерения ИХГС использует формирование дополнительного сигнала напряжения, сдвинутого на произвольный угол относительно входного и сигнала, инверсного входному. Поскольку инверторы, используемые для этих целей, могут обеспечивать погрешность в сотые доли процента, то это позволяет исключить угловую погрешность и погрешность по напряжению ИНВ. Проведенный анализ показывает, что наличие в сигналах высших гармоник приводит к существенному увеличению погрешности измерения ИХГС.

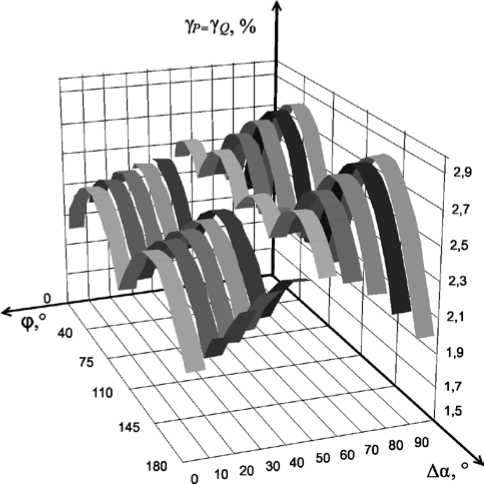
Рис. 5. Графики зависимости γ P =γ Q от Δα и φ

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 13-08-00173-а).