МЕТОД ИЗМЕРЕНИЯ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ С ОПРЕДЕЛЕНИЕМ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЙ И РАССТОЯНИЯ ДО ИСТОЧНИКА ПОЛЯ

Среди большого многообразия методов измерений напряженности электрического поля (ЭП) [1–7], направленных на повышение точности измерений, чувствительности, упрощения процесса измерений и др., выделяется новый метод — метод измерения по среднему значению [8, 9]. Для реализации метода измерений требуется иметь два измеренных значения напряженности E 1 и E 2 в одной точке поля, в которой напряженность до внесения датчика была E 0 . Значения напряженностей E 1 и E 2 отличаются от напряженности E 0 на значение погрешности. Неотъемлемым условием метода измерений по среднему значению является противоположность по знаку этих погрешностей.

Использование метода измерения по среднему значению потребовало создания датчиков напряженности ЭП (НЭП) нового типа — сдвоенных датчиков, основанных на явлении электрической индукции [10, 11]. Введение их расширило номенклатуру датчиков НЭП.

До настоящего времени были известны элек-троиндукционные датчики НЭП двух типов: одинарные и двойные [12]. Одинарные датчики имеют один чувствительный элемент по каждой координатной оси относительно основания датчика. Такие датчики чувствительны к синфазным навод- кам и помехам. Двойные датчики состоят из двух одинарных датчиков и имеют два диаметрально противоположных чувствительных элемента относительно основания датчика по каждой координатной оси. Датчики такого типа в дифференциальном включении нивелируют влияние синфазных наводок и помех. К одинарным и двойным датчикам присоединились сдвоенные датчики. Особенностью сдвоенных датчиков является совмещение двух двойных датчиков в одном. В этих датчиках по каждой координатной оси располагаются два двойных датчика. Такое техническое решение позволило сдвоенному датчику создавать два выходных сигнала, пропорциональных напряженностям E1 и E2, измеренным в одной точке поля с противоположными по знаку погрешностями. Наличие избыточной информации о напряженности поля, а именно двух значений E1 и E2, можно попытаться использовать для определения расстояния до источника поля и определения погрешности измерения E0 результата измерения модуля вектора E.

Дальнейшая работа будет построена на использовании сдвоенного однокоординатного датчика НЭП при его ориентации по направлению ЭП.

В связи с этим целью данной работы является создание нового метода измерений напряженности ЭП на основе сдвоенного однокоординатного дат- чика, позволяющего определять погрешность результата измерений и расстояние до источника поля.

ПОСТАНОВКА ЗАДАЧИ

Для достижения поставленной цели необходимо решить следующие задачи:

• 1)    дать характеристику сдвоенного датчика напряженности ЭП и подтвердить его пригодность для одновременного измерения двух значений напряженности Е\ и Ei в одной точке поля и возможность применения в новом методе измерений;

• 2)    установить эмпирическую зависимость параметра а = R / d, характеризующего пространственный диапазон измерения (7? — радиус сферического основания датчика, d — расстояние от центра датчика до источника поля) от отношения измеренных напряженностей к_ц = EJ Е^;

• 3)    разработать теоретические основы построения нового метода измерений, позволяющего определять модуль вектора напряженности электрического поля, а также его погрешность и расстояние до источника поля;

• 4)    предложить новый метод измерения напряженности электрического поля с определением погрешности измерения и расстояния до источника поля;

• 5)    доказать численным экспериментом адекватность нового метода измерений.

СДВОЕННЫЙ ДАТЧИК НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Необходимый для реализации метода измерений сдвоенный датчик, позволяющий в данной точке поля одновременно измерять два значения напряженностей Е\ и Е^ описан в работах [8, 9] и представлен на рис. 1.

Электроиндукционный сдвоенный датчик состоит из механической и измерительной частей. Механическая часть объединяет два датчика и представлена проводящим сферическим основанием 1, двумя чувствительными элементами 2 и 3 в форме сферических сегментов, двумя чувствительными элементами 4 и 5 в форме сферических слоев 4 и 5. Измерительная часть представлена двумя дифференциальными интеграторами тока (ДИТ1) 6, (ДИТ2) 7 и сумматором 8.

Чувствительные элементы 2 и 3 первого датчика выполнены с угловыми размерами 0О=45°. Датчик с такими угловыми размерами чувствительных элементов представлен в [12]. Сферические слои 4 и 5 являются частями чувствительных элементов (2+4) и (3+5), входящими в состав второго датчика. Они в сумме образуют чувствительные элементы в форме полусферы, имеющей угловой размер 0о = 90°. Датчик с такими угловыми размерами чувствительных элементов представлен в [13]. Все чувствительные элементы изолированы между собой и сферическим основанием.

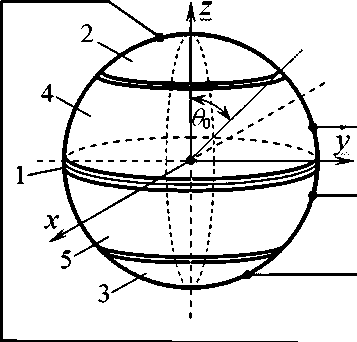
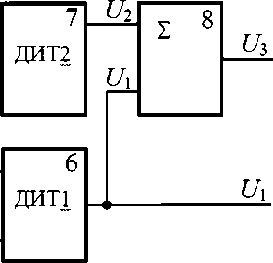
Рис. 1. Сдвоенный датчик напряженности электрического поля.

1 — проводящее сферическое основание; 2, 3 — чувствительные элементы в форме сферических сегментов; 4, 5 — чувствительные элементы в форме сферических слоев; ДИТ1 (6), ДИТ2 (7) — дифференциальные интеграторы тока; 2 (8) — сумматор

Получайте e-mail уведомления о выходе нового номера журнала. Подписка на странице

Дифференциальные интеграторы тока 6 и 7 снимают разности зарядов с диаметрально противоположных электродов датчика 2, 3 и 4, 5 и преобразуют их в напряжения U 1 ( t ) и U 2 ( t ), пропорциональные напряженности ЭП E . Напряжение U 1 ( t ) = kE 1 является выходным напряжением первого датчика. Выходное напряжение U 3 ( t ) = kE второго датчика получается суммированием напряжений U 1 ( t ) и U 2 ( t ) сумматором 8, объединяющим электрические заряды с элементов 2+4 и 3+5. Таким образом, сдвоенным датчиком формируются напряжения U 1 ( t ) и U 3 ( t ), пропорциональные напряженностям Е 1 и Е 2 , которые необходимы для реализации метода измерений.

§ 1 ( a ) =

= 100 x

X

V

ТЕОРИЯ

В основе теоретического обоснования нового метода измерений положены следующие априорно известные факты:

• 1)    Е 1 и Е 2 — два одновременно измеренных в одной точке ЭП с напряженностью E 0 значения напряженностей;

• 2)    значения напряженностей Е 1 и Е 2 определены с противоположными по знаку погрешностями, соответственно равными + δ 1 и – δ 2 ;

• 3)    значения погрешностей + δ 1 и – δ 2 определяются по известной формуле [14]

§( a ) = 100 X

.      . X

3 a ² sin ² θ ₀

—

3 a^{2 Х}

V1 — V2 a + a )

л

5₂(a ) = 100 x

3 a ²

2^1 + a⁴

V

—

—

1 — a ²

V1 + a a

—

.

,

С учетом погрешностей δ 1 ( a ) и δ 2 ( a ) можно за-

писать

E 1 ( a ) = E 0 [ 1 + 5 1 ( a ) ] и E 2 ( a ) = E 0 [ 1 + § 2 ( a ) ] , (4)

где E 0 — напряженность ЭП в точке измерения до внесения датчика.

Используя рассчитанные по выражениям (2)–(4) значения Е 1 ( a ) и Е 2 ( a ), введем в рассмотрение коэффициент k 0 ( a ) и рассчитаем его значения по формуле

k ₀( a )

E 1 ( a )

E ₂( a ).

X 2

V

1 - a a

1 — — 2 a cos6₀ + a²

1 - a ²

\

Результаты расчетов запишем в табл. 1.

По данным табл. 1 составлена эмпирическая формула функциональной зависимости a ( k 0 )

-

1 + 2 a cos 0 ₀ + a²

-

a = R / d = 1.123/ k 0 — 0.94 — 0.21.          (6)

полученной в результате исследования взаимодействия сферического датчика с полем точечного заряда. В выражении (1): a = R / d — пространственный диапазон измерений (относительное расстояние до источника поля); R — радиус сферического основания датчика; d — расстояние от центра сферического основания датчика до источника поля; θ 0 — угловой размер чувствительного элемента.

Выражение (1) позволяет рассчитать погрешности δ 1 и δ 2 для первого и второго датчиков, входящих в состав сдвоенного датчика. Для первого датчика с угловым размером 6₀ = 45 ° и второго датчика с угловым размером 6₀ = 90 ° чувствительных элементов погрешности δ 1 ( a ) и δ 2 ( a ) будут соответственно равны

Табл. 1. Значения коэффициента k 0 в зависимости от пространственного диапазона измерения a

a	k 0	a	k 0
0.05	1.004	0.55	1.423
0.1	1.015	0.60	1.495
0.15	1.033	0.65	1.568
0.20	1.058	0.70	1.64
0.25	1.091	0.75	1.711
0.30	1.131	0.80	1.779
0.35	1.178	0.85	1.843
0.40	1.231	0.90	1.901
0.45	1.29	0.95	1.954
0.50	1.355	—	—

Выражение (6) позволяет по коэффициенту k 0 определять относительное расстояние a до источника поля в каждой точка измерений. Зная относительное расстояние a , по выражениям (2) и (3) можно найти погрешности δ 1 и δ 2 полученных в каждой точке измерений двух измеренных значений Е 1 и Е 2 .

Метод измерений, предложенный авторами в работе [9], рекомендует нахождение результата измерений как среднее из двух измеренный значений Е 1 и Е 2 . Это позволяет уменьшить погрешность измерения напряженности E исходного ЭП E 0 .

Действительно, если учесть при нахождении среднего значения выражения (4), то получим

Е = Е 1 + Е 2 = Е « [ 1 +      1- Е о (1 + 6 ),     (7)

где

₆ = 6 1+ 6 2 2

—

погрешность среднего значения напряженности Е . В выражении (8) погрешность δ 1 положительная, а погрешность δ 2 отрицательная.

Таким образом, вычисляя в каждой точке измерения k 0 по выражению (5) и относительное расстояние a по выражению (6), можно по выражениям (2), (3) и (8) определить расстояние d = R / a до источника поля, погрешности δ 1 , δ 2 , δ измеренных значений Е 1 и Е 2 и результата измерения Е в данной точке измерения.

Определяя результат измерения E как среднее значение двух одновременно измеренных в одной точке ЭП напряженностей Е 1 и Е 2 , достигаем уменьшения результирующей погрешности δ измерения E . График, подтверждающий уменьшение погрешности δ , построенной в зависимости от пространственного диапазона a , представлен на рис. 2.

Согласно графику погрешность измерения положительна и не превышает 4.6% во всем пространственном диапазоне a от нуля до единицы.

На основании полученных результатов можно сформулировать новый метод измерения напряженности ЭП. Последовательность действий, реализующих предлагаемый метод измерений, сводится к следующему:

• 1)    помещению сдвоенного датчика в исследуемую точку ЭП;

• 2)    ориентации сдвоенного датчика в ЭП по направлению поля;

• 3)    измерению одновременно двух модулей вектора напряженности ЭП E 1 и E 2 в данной точке пространства;

  

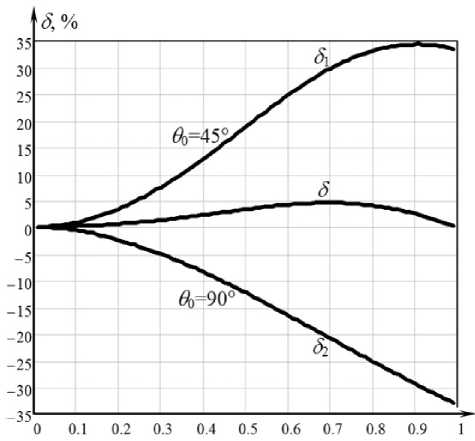
  a = R / d

  Рис. 2. Графики погрешностей δ 1 ( a ) и δ 2 ( a ) датчиков с угловые размерами чувствительных элементов 9₀ = 45 ° и 9₀ = 90 ° и погрешности 6^a )

  
  

• 4)    вычислению по измеренным значениям Е 1 и Е 2 коэффициента k 0 = E 1 / E 2 ;

• 5)    вычислению по формуле a - R / d -- 1.123/ k — 0-94 — 0.21 относительного расстояния до источника поля;

• 6)    нахождению среднего значения модуля вектора напряженности электрического поля Е = = ( Е 1 + Е 2 ) / 2, принимаемого за результат измерения;

• 7)    определению по найденным значениям k 0 и a погрешностей δ 1 , δ 2 и δ измеренных Е 1 , Е 2 и вычисленного Е значений. Погрешности определяются по выражениям (2), (3) и (8).

Поскольку погрешности δ 1 , δ 2 сдвоенного датчика получены при его нахождении в поле точечного заряда, то важно отметить, что датчик в реальных полях будет измерять эквивалент напряженности поля точечного заряда.

ПОДТВЕРЖДЕНИЕ АДЕКВАТНОСТИ МЕТОДА

Подтверждение будем проводить численным экспериментом. Для этого по формулам (2) и (3) для выбранных значений пространственного диапазона a рассчитаем погрешности измерений δ 1 ( a ) и 6 z ( a ) датчиков с угловыми размерами 6₀ = 45 ° и 6₀ = 90 ° их чувствительных элементов. Результаты расчета запишем в табл. 2. В нее же запишем погрешность δ результата измерений.

Табл. 2. Рассчитанные по (2), (3) значения погрешностей δ 1 ( a ), δ 2 ( a ) и результирующей погрешности δ ( a )

а	δ 1 , %	–δ 2 , %	δ , %
0.1	0.87	0.58	0.16
0.3	7.56	4.91	1.33
0.5	18.93	12.22	3.34
0.7	29.92	20.79	4.57
0.9	34.37	29.32	2.53
0.99	33.52	32.94	0.29

По выражению (4) рассчитаем относительные значения E ₁ ^* = E ₁ / E ₀ и E ₂ ^* = E ₂ / E ₀. Запишем их в табл. 3 и там же укажем среднее относительное значение E ^* = E / E ₀, рассчитанное по выражению (7).

Воспользовавшись выражением (5), рассчитаем в каждой точке измерений коэффициент k 0 и запишем его в табл. 4.

Табл. 3. Рассчитанные по (4) относительные значения напряженностей

а	E 1*	E 2*	E *
0.1	1.008	0.994	1
0.3	1.076	0.95	1.014
0.5	1.190	0.878	1.034
0.7	1.3	0.792	1.046
0.9	1.344	0.706	1.026
0.99	1.336	0.67	1.004

Подставим коэффициенты k 0 в эмпирическую формулу (6); определим предполагаемые значения a ^* параметра a , соответствующего данной точке измерений, и оценим погрешность расхождения γ между ними. По проведенным расчетам погрешность расхождения γ между эмпирически определенными параметрами a ^* и заданными параметрами a по модулю не превышает 5.7%. Результаты расчетов запишем также в табл. 4.

Вычисленные значения параметра a ^* из табл. 4 подставим в выражения (2) и (3) и рассчитаем погрешности δ 1 ^* и δ 2 ^* измеренных относительных значений напряженностей E 1 ^* и E 2 ^* первым и вторым датчиками и погрешность δ ^* результата измерений E ^*. Результаты расчетов запишем в табл. 5.

При сравнении данных табл. 2 и табл. 5 устанавливаем хорошее согласование погрешностей, рассчитанных по теоретическим значениям a и эмпирическим значениям a ^* пространственного диапазона измерений.

Таким образом, рассмотренный метод позволяет не только определить результат измерения E с малой погрешностью δ , но и инструментально определять как эту погрешность, так и расстояние до источника поля как d = R / a .

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Технический прогресс не стоит на месте. Он требует как можно больше возможностей применяемых как методов, так и средств измерений. Рассмотренный в работе метод сильно отличается от известных методов измерений, направленных в большинстве своем на измерение вектора напряженности ЭП, его модуля и составляющих. В пределах этих направлений известные методы обеспечивают: повышение чувствительности и точности измерений, упрощение процесса измерений и расширение пространственного диапазона измерений. В основе известных методов измерения

Табл. 4. Рассчитанные значения коэффициента k 0 , параметра a ^* по эмпирической формуле (6) и расхождения γ

а	k 0	* a	γ , %
0.1	1.014	0.095	–5.0
0.3	1.133	0.283	–5.7
0.5	1.355	0.513	2.6
0.7	1.64	0.73	4.3
0.9	1.904	0.893	–0.8
0.99	1.994	0.943	4.8

Табл. 5 . Рассчитанные значения погрешностей δ 1^* , δ 2^* и δ ^* через параметр a ^*

а	* a	δ 1* , %	–δ 2* , %	δ * , %
0.1	0.095	0.787	0.523	0.132
0.3	0.283	6.758	4.397	1.181
0.5	0.513	18.931	12.219	3.356
0.7	0.73	29.923	20.79	4.566
0.9	0.893	34.367	29.319	2.524
0.99	0.943	33.527	32.942	0.293

напряженности ЭП лежат одинарные и в большей части двойные электроиндукционные датчики. Создание датчика нового типа [10, 11] — сдвоенного датчика — позволило расширить его возможности, а именно одновременного измерения в одной точке поля двух значений напряженностей с противоположными по знаку погрешностями. Эта особенность сдвоенного датчика сделала возможным создание метода измерений, позволяющего не только измерять модуль вектора напряженности ЭП с повышенной точностью, но и инструментально определять его погрешность в данной точке измерений и расстояние от источника поля. Метод с такими возможностями является новым и рассматривается впервые [15].

ВЫВОДЫ

В результате проведенной работы дана характеристика сдвоенного датчика и обоснована его пригодность для построения нового метода измерений. Установлена эмпирическая зависимость относительного расстояния a от отношения напряженностей k 0 = E 1 / E 2. . На основании этого разработаны теоретические основы и предложение нового метода измерений, позволяющего определять модуль вектора напряженности электрического поля, а также его погрешность и расстояние до источника поля. Метод подтвержден численным экспериментом.