Метод измерения толщины срезов одноосных анизотропных кристаллов и термическое управление преобразованием пучка Бесселя

Одноосные кристаллы X -срезов (вырезанные параллельно оптической оси) используются в интерференционно-поляризационных фильтрах [1], на основе которых выделяются узкие спектральные линии [2], осуществляется дистанционный контроль концентрации газов [3], изменяется длина волны излучения лазеров [4]. Кристаллические фазовые пластины и фильтры также применяются для преобразования пучков [5–7] и способствуют освоению новых спектральных диапазонов, например, терагерцового [8].

Для получения требуемой спектральной характеристики интерференционно-поляризационных фильтров необходимо с высокой точностью знать оптическую разность хода h Δ n используемых фазовых пластин. При механических измерениях толщины h фазовых пластин высокого порядка m ~ 10–100 эта задача осложняется технологической вариацией двулучепреломления Δ n . Для материалов с высоким двулучепреломлением, необходимым для создания компактных интерференционно-поляризационных фильтров, использование механических измерителей практически исключается вследствие их недостаточной точности. Другая проблема возникает при освоении новых диапазонов, в которых неизвестна спектральная зависимость двулучепреломления Δ n (λ). Следовательно, для решения этих задач необходимы оптические методы измерения толщины h , двулучепреломления Δ n, оптической разности хода h Δ n.

В специальной литературе, посвящённой исследованию природных и искусственных кристаллов [9– 12], рассмотрены различные методы поляризационной микроскопии для измерения оптической разности хода hΔn и двупреломления Δn. Однако высокий порядок фазовых пластин, требуемый для получения узких спектров пропускания интерференционнополяризационных фильтров с λ/Δλ~103–105, затрудняет использование этих методов ввиду наложения цветных полос, характерного для кристаллов с большой оптической разностью хода hΔn. Вместе с тем поляризационно-интерференционный метод [9] потенциально наиболее точен, поскольку учитывает вариацию оптических свойств кристаллов. Однако теоретические основы данного метода требуют учёта влияния спектральных характеристик элементов схемы (источника, поляризаторов, кристалла, фотоприёмника), а также влияния ограничивающих апертур оснастки. Кроме этого, необходима метрологическая оценка точности и разрешающей способности поляризационно-интерференционного метода.

Целью работы было развитие поляризационноинтерференционных методов измерения толщины h , двулучепреломления Δ n и оптической разности хода h Δ n одноосных кристаллов X -среза. Поставленная цель достигается за счёт использования особенностей спектрального пропускания X -среза одноосного кристалла, установленного между поляризатором и анализатором.

Теоретические основы метода

Известно, что при падении параллельного пучка света на X-срез одноосного кристалла происходит его разделение на обыкновенную и необыкновенную волны [1]. Каждая из этих волн распространяется со своей фазовой скоростью, определяемой обыкновенным no(λ) и необыкновенным ne(λ) показателями преломления. С помощью анализатора осуществляется интерференционное сложение этих волн на выходе кристалла. Спектральное пропускание Iout(λ) структуры «поляризатор–кристалл–анализатор» зависит от толщины кристалла h, длины волны λ и спектральной зависимости двулучепреломления Δn(λ) = no(λ) – ne(λ). Следовательно, по виду спектрального пропускания Iout(λ) такой структуры можно судить о толщине кристалла h и/или его двулучепреломлении Δn(λ).

Вычислим пропускание Iout(λ) для азимутальных углов поляризатора γ1 =0°, кристалла γ2=45° и анализатора γ3 =0°. Для этого воспользуемся формулой [9] с поправкой на реальное пропускание основных оп- тических элементов схемы, спектральную характеристику источника и чувствительность фотоприёмника:

I out (^X) = I s (^X) S ph ( X ) T pa ( X ) T cr ( X ) x x | 0,5 + 0,5cos ( (2 n/X ) • h A n ( X ) ) ] ,

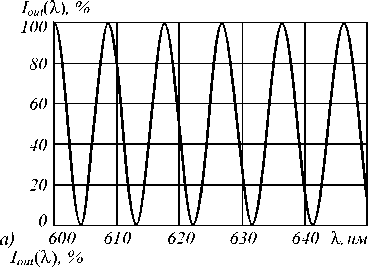
где Is(λ) – спектральная интенсивность источника излучения, W; Sph(λ) – спектральная чувствительность фотоприёмника, А/Вт; Tp,a(λ) – спектральное пропускание параллельно установленных поляризатора и анализатора, %; Tcr(λ) – спектр пропускания X-среза кристалла, %. При выполнении спектральных исследований предварительно производится измерение множителя Is(λ) Sph(λ) Tp,a(λ) (т.н. «базовая линия»), на который нормируются все последующие измерения. Поэтому в дальнейших расчётах величины Is(λ), Sph(λ), Tp,a(λ) не учитываются. Вычислим зависимость Iout(λ), полагая, что оси поляризатора, кристалла и анализатора ориентированы под азимутальными углами γ1 =0°, γ2 = 45°, γ3 =0°, а толщина X-среза кристалла (ниобат лития – LiNbO3) составляет 0,5 мм и 1,0 мм (рис. 1). При расчётах и дальней- ших измерениях показатели преломления кристалла вычислялись по формулам, приведённым в [10].

Из результатов расчётов следует, что I out (λ) имеет апериодический вид, причём период Δλ p увеличивается с ростом длины волны λ и уменьшается с увеличением толщины кристалла h . Для измерения толщины кристалла можно использовать длины волн λ 1 и λ 2 соседних максимумов I out (λ). Полагая, что λ 1 < λ 2 , запишем систему уравнений для нахождения толщины h и порядка интерференции m :

( 2 ^X 1 ) h A n ( X 1 ) = 2 n ( m + 1 ) , ( 2 n/X 2 ) h A n ( X ₂ ) = 2 n m.

Решая систему (2) относительно h и проводя замену вида Δ n (λ 1 ) = Δ n 1 , Δ n (λ 2 ) = Δ n 1 , получим искомое значение толщины кристалла:

h = ( X 1 X ₂)/( X ₂ A n 1 -X 1 A n 2 ). (3)

Из формулы (3) следует, что для кристаллов с большой оптической разностью хода h Δ n измерения лучше выполнять в длинноволновой части окна прозрачности, где расстояние между длинами волн λ 1 , λ 2 соседних максимумов больше. Для образцов с малой оптической разностью хода h Δ n , в т.ч. для анизотропных плёнок, необходимо проводить измерение λ 1 , λ 2 в коротковолновой части диапазона пропускания.

20 0

б)    600 610    620    630    640 X , нм

Рис. 1. Расчётное пропускание I out (λ) структуры «поляризатор–кристалл–анализатор» для X-среза кристалла LiNbO 3 при γ 1 = 0°, γ 2 = 45°, γ 3 = 0°: h = 0,5 мм (а), h = 1,0 мм (б)

Аналогичный подход может использоваться для определения спектральной зависимости двулучепреломления Δ n (λ) нового оптического материала или известного материала в осваиваемой части спектра. Пусть пропускание I out (λ) имеет вид чередующихся максимумов и минимумов, как показано на рис. 1. Поставим в соответствие соседним максимумам длины волн λ i , λ i +1 . Положим двулучепреломление на этих длинах волн приблизительно одинаковым Δ n i ≈ Δ n i+1 , что справедливо для достаточно толстых образцов с λ i ≈ λ i +1 . Тогда можно вычислить дискретные значения двулучепреломлений в этих точках по формуле Δ n i ≈ λ i λ i +1 / ( λ i +1 – λ i ) / h при известной толщине образца h . Для улучшения разрешающей способности метода можно использовать не только максимумы, но и минимумы спектрального пропускания I out (λ).

Вычислим абсолютную погрешность Δ h рассмотренного метода измерения толщины. Заметим, что погрешности (∂ h /∂λ 1 )Δλ 1 и (∂ h /∂λ 2 )Δλ 2 являются сильно коррелированными, поскольку источником Δλ 1 , Δλ 2 является один прибор – спектрометр. Аналогичным образом коррелированными оказываются погрешности (∂ h /∂Δ n 1 )Δ(Δ n 1 ) и (∂ h /∂Δ n 2 )Δ(Δ n 2 ). Между собой эти пары погрешностей не коррелированы, поскольку их источниками являются различные приборы [13]. Следовательно, расчёт результирующей абсолютной погрешности Δ h следует проводить по формуле (4). В (4) отсутствует учёт температурного изменения двулучепреломления Δ n , т.к. в лабораторных условиях оно вносит пренебрежимо малую погрешность.

A h = ±

^f f d h .^ dX

AX 1 +

f d h ) I dX ₂ J

AX 2

I d h I

+ I зТ" IA(An) ( dAnJ

+

d h dA n ₂

I ²

A(An2 )

где Δλ 1 , Δλ 2 – абсолютные погрешности измерения длин волн λ 1 , λ 2 соседних максимумов I out (λ), нм; Δ(Δ n 1 ), Δ(Δ n 2 ) – абсолютные погрешности измерения двулучепреломления кристалла на длинах волн λ 1 , λ 2 . Для современных спектрометров величина Δλ не превосходит 0,1 нм. Погрешность определения показателей преломления n o (λ), n e (λ) и, следовательно, двулучепреломления Δ(Δ n 1 ), Δ(Δ n 2 ) составляет 5×10^–5. Погрешность измерения толщины (4) для X -среза ниоба-та лития, использованного в эксперименте, с h = 1,052 мм с λ 1 = 632,10 нм, λ 2 = 635,65 нм составила Δ h = ±0,6 мкм.

В формулу (4) не входят значения азимутальных углов анализатора γ 1 , кристалла γ 2 и анализатора γ 3 . Это обусловлено формальным заданием величин γ 1 =0°, γ 2 =45°, γ 3 =0° при выводе (1). На практике азимутальные углы будут немного отличаться от номинальных значений, что окажет влияние на точность измерения. Выполним анализ влияния погрешности установки азимутальных углов анализатора γ 1 , кристалла γ 2 и анализатора γ 3 . При отличии γ 1 – γ 2 от номинального значения 45° в кристалле будут возбуждаться неравные по амплитуде обыкновенная и необыкновенная волны. В результате спектральное пропускание I out (λ) в минимумах не будет нулевым. Аналогичное влияние окажет отличие углов γ 2 – γ 3 от значения 45°, поскольку сложение обыкновенной и необыкновенной волн на выходе кристалла будет осуществляться с различными весовыми коэффициентами. Таким образом, неточность установки азимутальных углов равнозначна сглаживанию зависимости I out (λ), что потенциально затрудняет точное определение спектрального положения λ 1 , λ 2 пологих максимумов. Однако при реальных погрешностях γ 1 , γ 2 , γ 3 в 0,1–1° это оказывает незначительное влияние на определение характерных длин волн λ 1 , λ 2 , находящееся в пределах разрешающей способности спектрометра.

Экспериментальные результаты

В качестве кристалла X -среза использовался кристалл конгруэнтного ниобата лития производства ООО «ЭЛАН+» (Россия, СПб.). Кристаллы полировались алмазной суспензией до чистоты поверхности PIII по ГОСТ 11141-84, неплоскостности поверхности – не более 10′′, шероховатости R a <2 нм. Перед измерениями поверхности кристаллов обезжиривались и промывались в бидистиллированной воде. Толщина кристалла измерялась цифровым микрометром МКЦ-25 и составляла h =1,052±0,002 мм.

Измерение спектра пропускания Iout(λ) в диапазоне 600–650 нм с разрешением 0,05 нм осуществлялось на спектрофотометре Shimadzu UV-2450. При измерении кристалл помещался между плёночным поляризатором и анализатором оптического качества с коэффициентом поляризации не менее 104 в диапазоне 600–650 нм. Азимутальные углы поляризатора, кристалла и анализатора составляли γ1 =±0,5°, γ2=45,0±0,5°, γ3=±0,5°. Перед исследованием спектрального пропускания Iout(λ) проводилось измерение спектра Is(λ)Sph(λ)Tp,a(λ), входящего в (1) при установленных в рабочие положения поляризаторе и анализаторе. Азимутальный угол поляризатора соответствовал преимущественно вертикальной поляризации источника излучения спектрофотометра, что улучшало отношение сигнал/шум и точность определения λ1, λ2. Результаты измерения спектра пропускания Iout(λ) показаны на рис. 2.

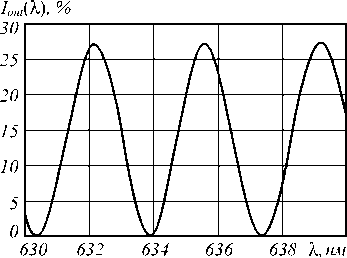
Рис. 2. Измеренное пропускание I out (λ) структуры «поляризатор-кристалл-анализатор» для X-среза кристалла LiNbO 3 толщиной h = 1,052±0,002 мм

Измерение подтвердило периодический характер спектра пропускания структуры «поляризатор-крис-талл-анализатор». Уменьшение максимального пропускания до 27–28 % по сравнению с расчётными данными на рис. 1 объясняется влиянием апертуры поворотной оправы кристалла и отражением от поверхностей кристалла. Возрастание зависимости I out (λ) обусловлено спектром пропускания кристалла ниобата лития T cr (λ), имеющего подъём на 0,5–1,0% в диапазоне 600–700 нм.

Характерные длины волн максимумов пропускания I out (λ) составили λ 1 = 632,10 нм, λ 2 = 635,65 нм. Согласно формулам (3), (4) это соответствует толщине кристалла h = 1,0530±0,0006 мм, что находится в пределах погрешности электронно-механического измерения толщины h = 1,0520±0,0020 мм.

Исследование возможности управления преобразованием пучков Бесселя за счёт изменения толщины кристалла

Дальнейшее развитие оптической техники и технологии требует создания приборов и методов формирования пучков Бесселя с вихревой фазой. Одним из путей решения этой задачи является использование анизотропных кристаллов. Теоретические исследования [5–7] показали, что в одноосных кристаллах происходит периодическое преобразование непараксиально распространяющегося вдоль оси пучка Бесселя нулевого порядка в вихревой пучок Бесселя второго порядка. В экспериментальных работах [15, 16] было отмечено повышение эффективности преобразования и уменьшение пространственного периода преобразования с ростом числовой апертуры пучка и двулучепреломления кристалла. Однако в этих работах не совсем точно согласованы длина кристалла и период преобразования, поскольку использовались готовые кристаллы и элементы Бессель-оптики. В результате не удалось достичь полного преобразования пучков, хотя всё равно степень преобразования была повышена по сравнению с работой [5]. Таким образом, задача достижения полного преобразования пучков в кристалле по-прежнему актуальна.

Как было показано ранее [14], период повторения формы пучка в кристалле p зависит от показателей преломления кристалла и числовой апертуры аксикона. Причём для аксиконов с числовой апертурой 0,15 – 0,50 период составляет десятки микрометров. Следовательно, для формирования заданного пучка толщина кристалла должна выдерживаться с микронными допусками, что затрудняется высокой трудоёмкостью изготовления и вариацией свойств кристаллов.

Всё это заставляет искать методы управления оптическими параметрами уже изготовленных кристаллов для согласования периода преобразования с толщиной кристалла. Для осуществления подстройки подходят различные физические эффекты, изменяющие показатели преломления и/или толщину кристалла: термооптический, электрооптический, тензо-оптический, фоторефрактивный, температурное расширение кристалла и т.д. Так, в [17] проведено теоретическое исследование электрического управления орбитальным и угловым моментом моды Гаусса– Бесселя, распространяющейся в электрооптическом кристалле LiNbO 3 . В работе [18] рассмотрено электрооптическое преобразование мод Лаггера–Гаусса с правой и левой круговой поляризацией.

В нашей работе в качестве управляющего воздействия выбрано изменение температуры, влияющее на показатели преломления и толщину кристалла. Выбранный метод управления не обладает высоким быстродействием, свойственным электрооптическому эффекту. Однако он пригоден для создания лабораторных устройств научного назначения.

Численный анализ предложенного подхода

Механизм рассмотренного управления преобразованием пучка состоит: 1) в термическом расширении кристалла вдоль оси, 2) термооптическом изменении показателей преломления и двулучепреломления кристалла. Для выявления степени влияния каждого из рассмотренных выше динамических механизмов проведём их анализ, основанный на математических моделях [14–16].

Для расчёта распределения интенсивности пучка Бесселя на выходе с -среза одноосного кристалла I ( x , y ), освещаемого дифракционным аксиконом, в работе [14] была получена формула:

I ( x , y ) = 1 | C|² J 02 ( kax ² + y ² ) +

2 (5)

+^ |S|2 J2 (ka Jx2 + y2), где k = 2π/λ – волновой вектор; α – пространственная частота аксикона; J0, J2 – функции Бесселя 0-го и 2-го порядков; C, S – условные величины, равные:

^C = exP ( jkz Y o ) ⁺ exP ( jkz Y e ) ,

S = exp ( jkz y o ) - exp ( ^jkz Y e ) ,

где z – толщина кристалла; γ o , γ e – величины, определяющие направление распространения обыкновенного и необыкновенного пучков:

Y o = a] n o ^-a 2 ,

Y e = n" 2 ^-a 2 n 2 / n 2 ,

где no, ne – обыкновенный и необыкновенный показа- тели преломления кристалла.

Из формул (5)–(7) следует, что при заданных значениях λ, α, n o , n e вид пучка Бесселя определяется характеристическим отношением h / p , где h – толщина кристалла вдоль оси z , а p – период преобразования пучка в кристалле. Причём дробная часть этого отношения определяет вид выходного пучка, а его полное значение – чувствительность к температурному изменению оптических характеристик кристалла и его толщины.

Дробная часть h / p может быть вычислена для каждой температуры на основе экспериментальных данных. Для этого следует варьировать толщину кристалла h, выраженную в долях p, в формуле (6) до совпадения расчётного и измеренного распределений интенсивности I ( x,y ). Для расчёта периода пространственного преобразования пучка p , отсчитываемого вдоль с -оси (т.е. вдоль оптической оси) кристалла, используется формула [14]:

_     % p 2 (Yo -Ye ) .

Отношение h / p при начальной температуре 21,1 °C вычислялось по измеренной микрометром МКЦ-25 толщине кристалла h =15007±2 мкм и формуле (8). Величины h / p при температурах 45,7°С, 70,5°С определялись по совпадению расчётного и измеренного распределения интенсивности пучка на основе формул (5)–(8). Такой комбинированный подход наиболее удачен, поскольку позволяет точно определить начальную рабочую точку температурной характеристики I ( t, x, y ), вычислить и целую, и дробную части h / p .

При расчётах длина волны лазера составляла λ =0,6328 мкм, пространственная частота – α =0,159, показатели преломления – n o =1,6557, n e = 1,4852. Средний коэффициент теплового расширения CaCO 3 вдоль с -оси принимался равным ( 1 / h· d h /d t ) =26,3· 10^–6 1/град в диапазоне 0–80°C [19], а термооптические коэффициенты – d n o /d t =0,9·10^–6 1/град, d n e /d t =10,8· 10^–6 1/град [20].

Обработка экспериментальных данных показала, что для температур 21,1 °С, 45,7°С, 70,5°С отношение h/p составило 87,48, 87,39 и 87,28 соответственно. Таким образом, увеличение температуры на 49,4°С внесло регистрируемое изменение в 0,20p. При этом ожидаемое изменение, вычисленное на основе термооптических коэффициентов и коэффициента линейного расширения, составляет 0,19p (h/p =87,48, 87,39, 87,29). Полученное расхождение в 5 % может быть обусловлено погрешностью измерения температуры, отличием свойств механически зажатого кристалла от справочных, формой и стабильностью освещающего лазерного пучка. Лазерные пучки, рассчитанные по (5)–(8) для температур 21,1 °С, 45,7°С, 70,5°С, показаны на рис. 3.

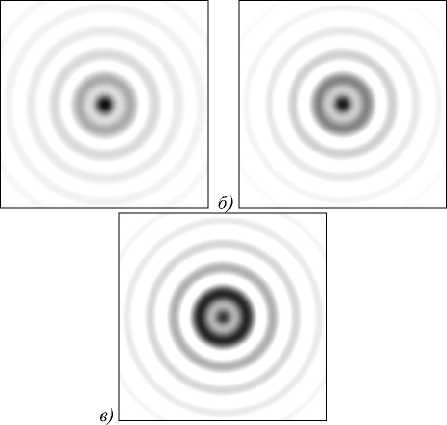
Рис. 3. Рассчитанные лазерные пучки при различных температурах (негативные изображения):

а) 21,1 °С, б) 45,7 °С, в) 70,5 °С

Период преобразования p , вычисленный на основе термооптических коэффициентов, увеличивается. Согласно (8) при 21,1 °С, 45,7 °С, 70,5 °С он принимает значения 171,55 мкм, 171,84 мкм, 172,14 мкм соответственно. Из этого следует противодействие механизма термооптического изменения показателей преломления и механизма теплового расширения кристалла. Это существенно снижает эффективность температурного преобразования пучков Бесселя на основе кристалла CaCO 3 . Для повышения чувствительности следует выбирать кристаллы с минимальными, а ещё лучше – отрицательными термооптическими коэффициентами.

Экспериментальное исследование термического управления

Для исследования термического управления преобразованием пучка Бесселя нулевого порядка в вихревой пучок второго порядка была собрана оптическая установка, схема которой показана на рис. 4. Термостатируемая оптико-механическая часть содержала дифракционный аксикон, с -срез кристалла CaCO 3 и микрообъектив, установленные на координатные и угловые оправы.

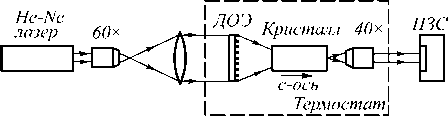
Рис. 4. Схема экспериментальной установки

Источником излучения служил гелий-неоновый лазер ЛГН-207А с линейно-поляризованным излучением. Расширение лазерного пучка производилось объективом 60× и плоско-выпуклой линзой диаметром 20 мм и фокусным расстоянием 150 мм. В качестве анизотропной среды использовался одноосный кристалл CaCO3 с размерами 8×8×15 мм. С-ось кристалла ориентировалась параллельно оптической оси схемы. Точное сведение обыкновенного и необыкновенного пучков обеспечивалось двумерной угловой оправой. Увеличение размеров выходного пучка осуществлялось 40× объективом с NA=0,65, превосходящей числовую апертуру ак-сикона. Распределение интенсивности выходного пучка фиксировалось чёрно-белой USB-видеокамерой DCM 310 с разрешением 3 МПкс и разрядностью аналого-цифрового преобразователя 8 бит.

Для формирования пучка Бесселя нулевого порядка был изготовлен амплитудный дифракционный ак-сикон диаметром 40 мм на стеклянной подложке с периодом колец 4 мкм (для λ = 0,6328 мкм соответствует угловой апертуре α = 0,159). Амплитудная маска аксикона формировалась на установке CLWS-200 методом термохимического окисления хрома с последующим химическим удалением немаскированных участков. Экспонирование маски фоторезиста производилось на установке CLWS-200 в векторном режиме, что обеспечивало отсутствие ступенчатых дефектов топологии и высокое качество формируемого пучка Бесселя. Фотография дифракционной маски (хром толщиной 100 нм), полученная на электронном микроскопе, показана на рис. 5.

Рис. 5. Фотография дифракционного аксикона с периодом колец 4 мкм

Ширина светлых и тёмных колец одинакова и составляет 2 мкм. В центральной части аксикона присутствуют два кольца с увеличенной шириной, необходимые для центрирования лазерного луча. Поскольку радиус внешнего широкого кольца хрома не превосходит 50 мкм, то вносимое им искажение пучка Бесселя будет наблюдаться на расстояниях до 350 мкм при апертуре α = 0,159. Поскольку кристалл располагался на расстоянии 5 мм от аксикона, а диаметр освещённой части аксикона составлял 15 мм, то наличие подобных дефектов не влияет на результаты экспериментов.

Аксикон, кристалл и объектив помещались в регулируемый термостат. Управление нагревателем термостата производилось измерителем-регулятором ОВЕН ТРМ 251. Датчик температуры имел номинальную статическую характеристику 100 М, погрешность измерения составляла до ±0,7ºС в исследуемом диапазоне температур 20–70ºС. Система управления позволяла поддерживать заданную температуру с отклонением не более ±0,1 ºС от измеряемой величины. Изменение температуры производилось с шагом около 25ºС, что занимало 15–20 мин. Для полного прогрева оптико-механической части она выдерживалась в термостате 1 ч для каждого измерения.

При измерениях было отмечено медленное координатно-угловое смещение пучка в плоскости матрицы видеокамеры, около 0,05 мм/ºС. Это было обусловлено обратимой температурной деформацией конструкции. Выдержка при заданной температуре останавливала это смещение. Возникающее расхождение сведённых ранее обыкновенного и необыкновенного пучков устранялось ручной юстировкой при установившейся температуре.

Кроме этого, фиксировались мерцание и хаотичное пространственное перемещение пучка с амплитудой до 0,1 мм при температурах более 25–30ºС. Это явление было обусловлено восходящими тепловыми потоками от нагревательного элемента, расположенного в нижней части термостата. Для снижения их влияния увеличивалось время достижения заданной температуры, что уменьшало скорость восходящих тепловых потоков, вертикальный градиент температуры и оптическую неоднородность воздуха.

На рис. 6 показаны экспериментальные результаты преобразования пучка Бесселя, наблюдаемого на выходе кристалла CaCO 3 при различных температурах.

Рис. 6. Фотографии лазерного пучка при различных температурах (негативные изображения): а) 21,1 °С, б) 45,7 °С, в) 70,5 °С

Сам факт, что при этом формируется пучок Бесселя, был теоретически, численно и экспериментально показан в работах [5, 6, 14–16].

На рис. 7 приведено радиальное распределение интенсивности пучков, представленных на рис. 6.

Они практически совпадают с рассчитанными пучками на рис. 3. Для более детального сравнения на рис. 7 совмещены сечения для экспериментальных и теоретических результатов. Следует отметить, что первое изображение хотя и выглядит как непреобразо-ванный пучок Бесселя нулевого порядка, в действительности уже имеет степень преобразования 0,5. Это определяется сочетанием длины кристалла и кривизны волнового фронта освещающего пучка. Из полученных результатов следует, что изменение температуры с 21,1 ºС до 70,5 ºС привело к существенному снижению интенсивности центрального максимума диаграммы направленности. Кажущееся падение мощности излучения на рис. 7 объясняется различной площадью дифракционных колец, что не отражено в радиальном сечении распределения интенсивности. Согласно измерениям, мощности пучков отличаются не более ±3 %.

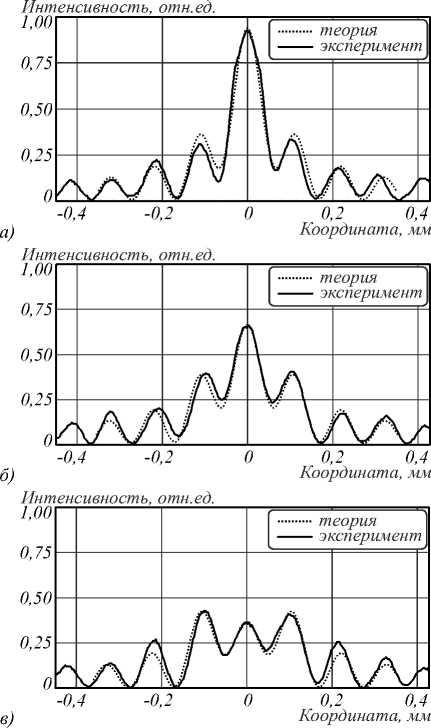
Рис. 7. Распределение интенсивности лазерного пучка при различных температурах:

а) 21,1 ºС, б) 45,7 ºС, в) 70,5 ºС

Заключение

Реализован поляризационно-интерференционный метод измерения толщины X-срезов одноосных кристаллов, основанный на интерференции обыкновенного и необыкновенного пучков на выходе анализатора. Экспериментальные результаты для ниобата лития показали совпадение толщины кристалла, измеренной электронно-механическим и предложенным методом в пределах допустимой погрешности. Расчёт погрешности измерения показал более высокую точность рассмотренного интерференционно-поляризационного метода (±0,6 мкм) по сравнению с механи- ческим измерителем (±2 мкм). Практическая значимость метода заключается в аттестации новых оптических материалов, в том числе в осваиваемых новых спектральных диапазонах.

Показана возможность управления преобразованием пучка Бесселя внутри кристалла CaCO 3 за счёт изменения его толщины. Экспериментально исследовано управление преобразованием пучков Бесселя нулевого порядка в вихревой пучок Бесселя второго порядка за счёт эффекта теплового линейного расширения кристалла и термооптического эффекта при его нагреве. При нагреве на 49,4 ° C получено изменение, равное 0,20 от пространственного периода полного преобразования пучка. Выявлено противодействие механизмов термооптического изменения показателей преломления и линейного расширения кристалла, снижающее эффективность преобразования. Предложено повышение чувствительности формы выходного пучка к температуре при использовании кристаллов с минимальными или отрицательными термооптическими коэффициентами за счёт увеличения апертуры освещающего аксикона и толщины кристалла. Рассмотренный подход позволяет создавать компактные твердотельные устройства управления оптическим излучением для использования в задачах лазерной обработки, литографии, манипуляции микрочастицами.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации и Российского фонда фундаментальных исследований (гранты РФФИ 16-07-00825, 14-02-97033р_поволжье_а).