Метод извлечения знаний из физически измеряемого сигнала обучения: проектирование баз знаний нечеткого регулятора

Разработка, развитие и реализация эффективных высоких наукоемких информационных технологий (ИТ) (создаваемых в различных областях науки и техники) неразрывно связаны с необходимостью разработки и повышения уровня интеллектуальности используемых процессов и систем управления, объективно учитывающие в законах управления контекстуально-зависимые физические эффекты, ограничения и информационные границы, реально существующие в конкретных моделях объекта управления (ОУ).

Важную роль при формировании уровня интеллектуальности системы автоматического управления (САУ) играет выбор используемого инструментария технологии интеллектуальных вычислений (ИВ) для проектирования соответствующей базы знаний (БЗ) при заданной цели управления [1].

В теории и проектировании систем управления в настоящее время большое внимание уделяется выявлению роли и эффективному применению робастных интеллектуальных систем управления (ИСУ) в интенсивном развитии и качественном совершенствовании современных высоких ИТ интеллектуального управления сложными физическими ОУ.

Сложность описания физических систем, в свою очередь, приводит к необходимости аппроксимации моделей ОУ и применению приближенных решений, которые не гарантируют необходимые и достаточные условия достижения цели управления в непредвиденных ситуациях и информационного риска. Поэтому в теории и систем управления одним из эффективных подходов снижения риска принятия решения (от неполноты описания модели ОУ) является разработка структур робастных ИСУ [1].

Данные структуры реализуют принцип компенсации информационной неопределенности описания модели ОУ за счет повышения уровня интеллектуальности традиционных систем управления [2, 3]. В частности, компенсация информационной неопределенности осуществляется за счет повышения интеллектуальности нижнего исполнительского уровня (с сохранением его функциональности) в виде соответствующих структур интеллектуальных нечетких регуляторов и соответственно спроектированных (с учетом в продукционных правилах информационного риска) самоорганизующихся робастных БЗ [4-6].

Таким образом, реализация данного принципа обеспечивает робастность ИСУ при неполном описании модели ОУ за счет учета в продукционных правилах проектируемых БЗ неточной (imperfect), извлекаемой из данной модели, информации и самоорганизации БЗ.

Динамическое поведение ОУ и системы управления (регулятора) служит источником объективных знаний для формирования БЗ, полнота (soundness) которой зависит от достоверности извлекаемой из конкретного источника информации. Неточность (imperfect) измерения (обусловленная объективной природой объекта) и недостоверность (unreliable) представления извлекаемой информации (например, из-за присутствия человеческого фактора в контуре управления) приводит к повышению информационного риска и возникновению непредвиденных ситуаций управления, компенсация которых для обеспечения робастности управления осуществляется применением необходимого уровня ИВ.

Выполнение и реализация новых физических (информационно-термодинамических) принципов интеллектуального робастного управления осуществляются на основе решения одной из принципиальных проблем построения объективных БЗ без участия эксперта. В этом случае необходимо, в отличие от прямой задачи (описания знаний количественными характеристиками), рассматривать решение обратной задачи теории искусственного интеллекта: извлечение, обработка и формирование знаний из количественных данных математического моделирования или физического эксперимента.

Принципиальное значение при формировании объективных БЗ в ИСУ имеет глобальная оценка физической и функциональной реализуемости аппроксимации моделей ОУ при наличии логикоинформационных границ и физических (термодинамических, квантово-релятивистских и др.) ограничений на описание реальных нелинейных ОУ [7].

На основе достоверности извлекаемого количества информации определяется информационная оценка приращения риска (статистической корректности) формируемого описания модели ОУ, и границ её применимости. Разработка логически непротиворечивых и адекватных (корректных) моделей ОУ с целью эффективной реализации ИСУ новыми видами современной техники является одной из актуальных проблем для современного этапа развития теории и систем управления.

В результате технология проектирования объективных БЗ на основе оптимизаторов БЗ на мягких и квантовых вычислениях исключает субъективизм экспертных оценок, обеспечивает достижение требуемого уровня робастности ИСУ [6].

В качестве классических состояний рассматриваются законы управления изменениями во времени коэффициентов усиления исполнительных автоматических устройств, которые формируют оптимальную управляющую силу (с минимальными потерями полезного ресурса в системе « объект управления + регулятор »).

Одним из важных элементов проектирования БЗ является разработка методологии и соответствующей программно-аппаратной поддержки процессов извлечения, обработки и формирования знаний из модели ОУ или количественных данных эксперимента с оценкой и контроля уровней робастности спроектированной структуры ИСУ.

В данной работе рассматривается способ повышения надежности и адаптивности САУ с помощью специального программного инструментария. Технология проектирования интеллектуальных регуляторов, представленная в работе, позволяет устранить субъективность при формировании БЗ. Использование инструментария позволяет также уменьшить время проектирования ИСУ и повысить ее робастность.

Объектом исследования в данной работе является проектирование БЗ робастных САУ с применением технологии мягких вычислений. Рассматривается технология проектирования ИСУ на примере классической задачи анализа динамики системы «каретка – перевернутый маятник». Динамика этого объекта является одной из типичных задач в теории управления, а решение этой задачи демонстрирует качество системы управления и метода проектирования системы управления.

Задачей управления является удержание маятника в вертикальном положении за счет оптимального регулирования выходных сигналов электродвигателей (исполнительных устройств).

Решить эту задачу позволяет интеллектуальный нечеткий ПИД-регулятор с глобальной отрицательной обратной связью, у которого коэффициенты усиления изменяются во времени по соответствующим законам управления.

Исходными источниками знаний при проектировании БЗ робастной ИСУ в данной работе являются динамическое поведение математической и физической модели ОУ (система "каретка – перевернутый маятник").

Для решения задачи извлечения, обработка и формирования знаний из количественных данных (математического моделирования или физического эксперимента) применяется программный инструментарий «Оптимизатор Баз Знаний» (ОБЗ) [8, 9], среда моделирования – MATLAB / Simulink и ОУ – физический макет – робот.

В работе рассмотрено два способа создания БЗ:

• -    Путем измерения результатов моделирования предварительно верифицированной математической модели.

• -    Путем измерения результатов моделирования физической модели ОУ.

Проведено сравнение спроектированных БЗ на основе математического моделирования и физического эксперимента.

Результатом работы является разработка способа и методики проектирования БЗ робастной ИСУ на основе математической модели ОУ или непосредственно физической модели ОУ без разработки математической модели ОУ.

Робастная структура ИСУ, с таким образом спроектированной БЗ, способна справляться с широким классом непредвиденных ситуаций управления.

Структура и основные функции оптимизатора баз знаний

Одним из основных результатов теории нечетких систем для теории и систем управления является теорема о наличии универсального аппроксиматора, утверждающая существование возможности аппроксимации сложных слабоструктурированных ОУ конечным числом продукционных правил в БЗ в виде нечеткого регулятора [1, 10].

Однако существование конструктивного алгоритма определения такого (необходимого и достаточного) конечного числа продукционных правил не установлено и в этом смысле теорема для системной инженерии не конструктивна.

На рис. 1 показана схема решения задачи определения необходимых параметров универсального аппроксиматора на основе оптимизатора БЗ (ОБЗ) на мягких вычислениях:

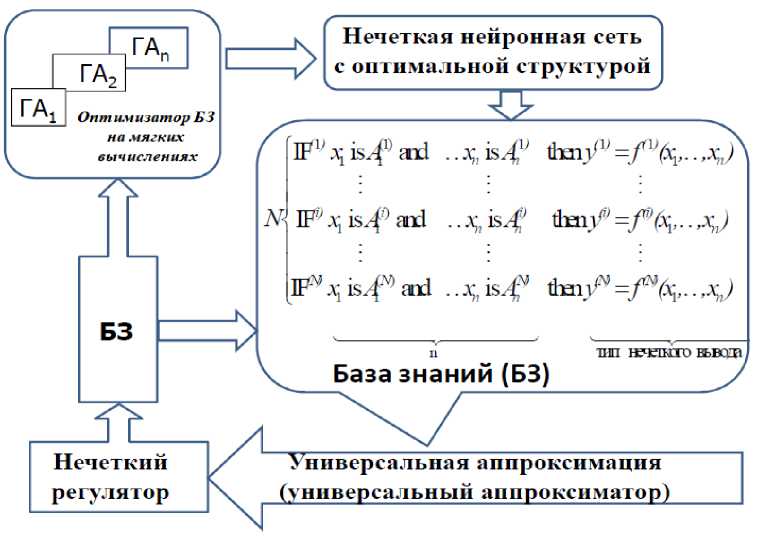
Рис. 1. Структурная схема определения параметров универсального аппроксиматора на основе ОБЗ

Данные определения и их применения в интеллектуальных нечетких регуляторах на основе ОБЗ на мягких вычислениях рассмотрены в [1, Глава 3].

Одной из основных проблем эффективного применения технологии мягких вычислений в задачах управления являлось решение следующих задач:

• -    объективное определение вида ФП и ее параметров в продукционных правилах в БЗ;

• -    определение оптимальной структуры нечетких нейронных сетей (ННС) в задачах обучения (аппроксимация обучающего сигнала с требуемой (заданной) ошибкой и с минимальным количеством продукционных правил в БЗ);

• -    применение генетического алгоритма (ГА) в задачах многокритериального управления при наличии дискретных ограничений на параметры ОУ.

Перечисленные проблемы были решены и апробированы на основе Оптимизатора Баз Знаний (ОБЗ) с применением технологии мягких вычислений [1, 8]. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок. В данном оптимизаторе используются три ГА, которые позволяют спроектировать оптимальную структуру нечеткого регулятора (вид и

Электронный журнал «Системный анализ в науке и образовании» Выпуск №1, 2013 год число ФП, их параметры, а также число самих правил нечеткого вывода), аппроксимирующей обучающий сигнал с требуемой ошибкой.

При этом автоматически проектируется оптимальная структуры нечеткой нейронной сети и универсального аппроксиматора в виде нечеткого регулятора.

Объединение методологий стохастического и нечеткого моделирования ИСУ в инструментарии ОБЗ позволило повысить уровень робастности проектируемых БЗ и решать сложные задачи формирования объективных знаний [4].

Таким образом, нечеткий регулятор является центральным элементом ИСУ и вырабатывает управляющие сигналы изменения во времени (законы управления) коэффициентами усиления k_p , k_d , k_i ПИД-регулятора основан на БЗ, которая интегрирована в интеллектуальный контроллер. Структурно БЗ состоит из продукционных правил, которые включают нечеткие входные и выходные значения функции принадлежности лингвистических переменных.

Наиболее актуальной проблемой при создании ИСУ является получение оптимальной и робастной БЗ, которая гарантирует высокий уровень качества управления. При проектировании базы присутствуют трудности, связанные со сложностью динамической системы и наличием шумов в системе измерения и управления.

Применительно к проектированию ИСУ, мягкие вычисления представляют собой комбинацию из следующих подходов: теория нечетких системы, генетические алгоритмы и нечеткие нейронные сети.

Функциональная структура ИСУ с блоками нечеткого регулятора и ОБЗ на мягких вычислениях представлена на рис. 2.

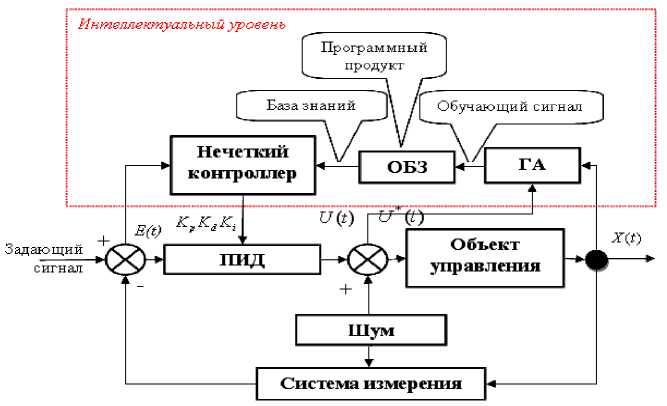
Рис. 2. Структура ИСУ с нечетким регулятором и оптимизатором БЗ

Такая структура включает одновременно следующие качества управления: управляемость, точность и устойчивость (нижний уровень управления – САУ), а также обучение и адаптация (верхний интеллектуальный уровень управления – нечеткий регулятор с БЗ).

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из результатов измерений динамических параметров физической модели ОУ.

ОС является источником знаний и представляет собой массив данных, разделенный на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде, каждый из составляющих сигналов является выборочной (репрезентативной) траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая корреляция между входными и выходными сигналами. Например, в случае аппрок- симации некоторого управляющего сигнала, входными компонентами могут являться ошибка управления, интеграл ошибки и ее производная, а выходным компонентом – требуемое значение управляющего воздействия, либо некоторые настраиваемые параметры системы управления, например коэффициенты усиления ПИД-регулятора. Пример ОС приведен на рис. 3.

e	ё	1 e^ 0	k„	к
-0. 01	-0. 01	-0. 01	13. 38	0.48	20.13
-0. 02	-0. 01	-0. 04	13. 38	0.48	20.13
-0. 04	-0. 01	-0. 07	13. 38	0.48	20.13
-0. 05	-0. 01	-0.12	13. 38	0.48	20.13
0. 25	-0. 02	7. 67	14. 20	0. 30	16. 26
0.18	-0. 07	7. 84	14. 20	0. 30	16. 26

Рис. 3. Обучающий сигнал

На рис. 3, входными данными для нечёткого регулятора является вектор ошибки. Он состоит из ошибки управления e ( t ), интеграла ошибки управления ie = j edt и скорости изменения ошибки управления e ( t ).

Выходными данными нечеткого регулятора является вектор, состоящий из значений коэффициентов усиления k_p , k_d , k_i ПИД-регулятора, значения которых применяются в формировании управляющего воздействия в виде:

t u (t) = kp (t) e (t) + kt (t )j edt + kd (t) e( t).                            (1)

Структурно ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА 1 , ГА 2 , ГА 3 ), оптимизирующих отдельные компоненты БЗ [1].

Структура ОБЗ и базовые шаги оптимизации представлены на рис. 4.

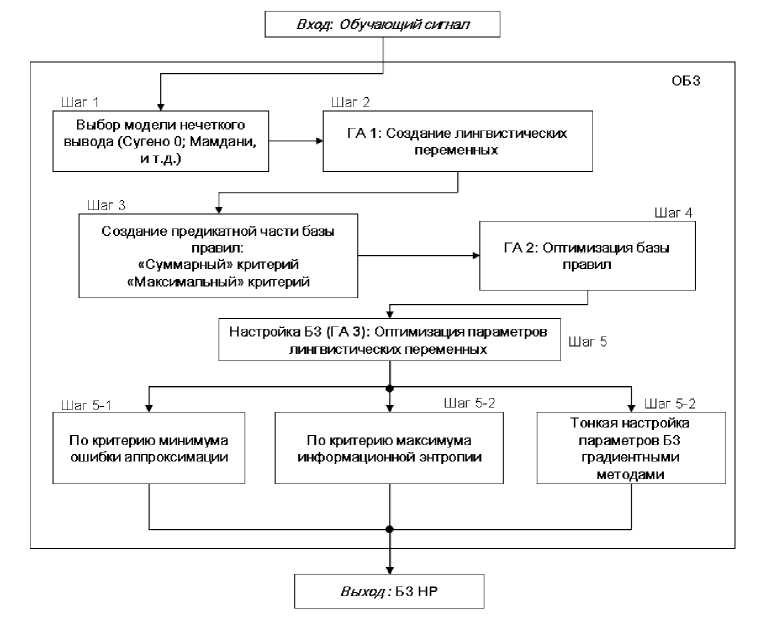
Рис. 4. Структура ОБЗ и шаги оптимизации БЗ

Рассмотрим шаги алгоритма оптимизации [1, 11]:

• -    Шаг 1: Выбор модели нечёткого вывода . Пользователь определяет тип нечёткой модели вывода (Сугено, Мамдани, и т.д.), и число входных и выходных переменных.

• -    Шаг 2: Создание лингвистических переменных . С помощью ГА 1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности (треугольная, Гауссовская и т.д.).

• -    Шаг 3: Создание базы правил . На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии со следующими двумя критериями:

« суммарный » критерий : выбрать только те правила, которые удовлетворяют следующему условию:

R otal _ fr >  TL ,                                             (2)

где TL (threshold level) – заданный (вручную или выбранный автоматически) уровень активации правила, и

R total _ fr = ^ R fr ⁽ t k ) , и R fr ⁽ tk ) = П^ У 1 ⁽ x 1 ⁽ t^k ^ ^ j 2 ⁽ x 2 ⁽ t^{k ))} ,."’ ^ jn ⁽ x n ⁽ t^{k )) ]} ,            ⁽³⁾

k = 1

где t_k - моменты времени, k = 1,..., N , N - равно числу точек в управляющем сигнале; ^ j_k ( x k ), k = 1,..., N — функции принадлежности входных переменных, l - индекс правила в БЗ; символ «П» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение).

« максимальный » критерий : выбрать только те правила, которые удовлетворяют условию:

max R fr ( t ) >  TL .                                      (4)

t

• -    Шаг 4: Оптимизация базы правил . С помощью ГА 2 оптимизируются правые части правил БЗ. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага 5 это решение может быть локально улучшено.

• -    Шаг 5: Настройка базы правил . С помощью ГА 3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных (с точки зрения заданной функции пригодности ГА). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем (шаги 5-1, 5-2 на рис. 3) . На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (см. шаг 5-3 на рис. 3).

Результатом аппроксимации ОС является построенная БЗ нечеткого регулятора, включающая конечное множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР.

Таким образом, результатом проектирования является требуемый тип универсального аппроксиматора в виде нечеткого регулятора с оптимальной структурой БЗ.

Математическая модель системы и объекта управления

Модель ОУ в виде одноосевой каретки с закреплённым на оси перевёрнутым вертикальным маятником, свободно вращающимся вокруг оси, показана на рис. 5. Динамика этого ОУ описывается системой дифференциальных уравнений второго порядка (5), выводимых, с учетом сил трения и упругости каретки, из баланса моментов и проекций сил на горизонтальную ось Z:

z _ u + ^ (t) - a 1 z — a 2 z + ml ( 9 sin 9 cos 9 )

<

g sin 9 + cos 9

9 =----------

т с + m

^ u + < ^ (t) + a 1 z + a 2 z — ml 9 ² sin 9

— k9

к

т с + m

l ( ⁴

—

m cos² 9

.

к 3 тс + m 7

Система позволяет вычислить управляющее воздействие на двигатели, необходимое для поддержания маятника в вертикальном положении при движении каретки:

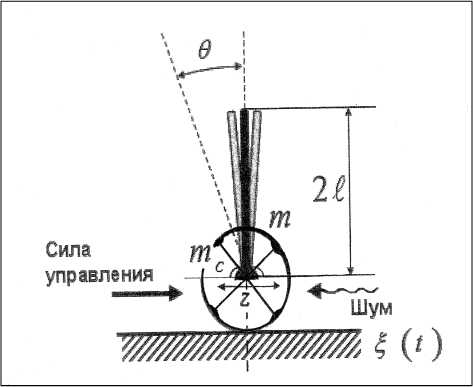
Рис. 5. Модель балансирующего макета «каретка - перевернутый маятник»

В системе уравнений (1) z и θ – обобщенные координаты; g – ускорение свободного падения (9.8 m /sec ² ), m_c – масса оси вращения (аналог массы подвижной каретки), m – масса перевернутого маятника (называемого «шест»), l – половина эффективной длины маятника, k и а ₁ коэффициенты трения о поверхность горизонтального перемещения вдоль оси z и в оси вращения θ , соответственно, а ₂ – сила упругости, препятствующая перемещению тележки, ξ ( t ) – внешний стохастический шум, а u – сила управления.

Структура компьютерной модели «каретка – перевернутый маятник», выполненная в среде моделирования MatLab/Simulink, представлена на рис. 6.

Данная модель включает в себя ПИД-регулятор, шумы в системе управления и измерения, а также блок, формирующий сигнал для регулятора.

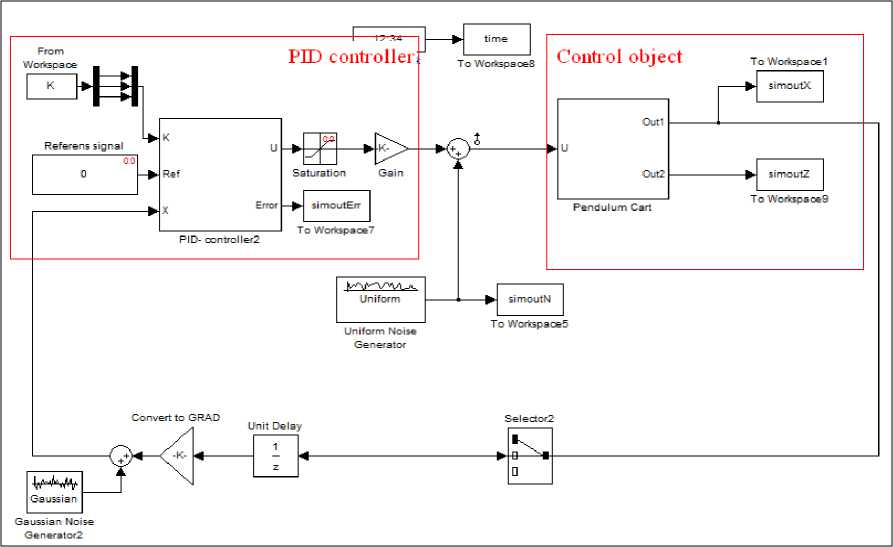
Рис. 6. Структура Matlab-модели с ПИД-регулятором

Эксперименты проводились на физической модели робота, представленной на рис. 7а, и стенде для экспериментов. Стенд оборудован несколькими покрытиями для имитации непредвиденной ситуации и представлен на рис. 7б.

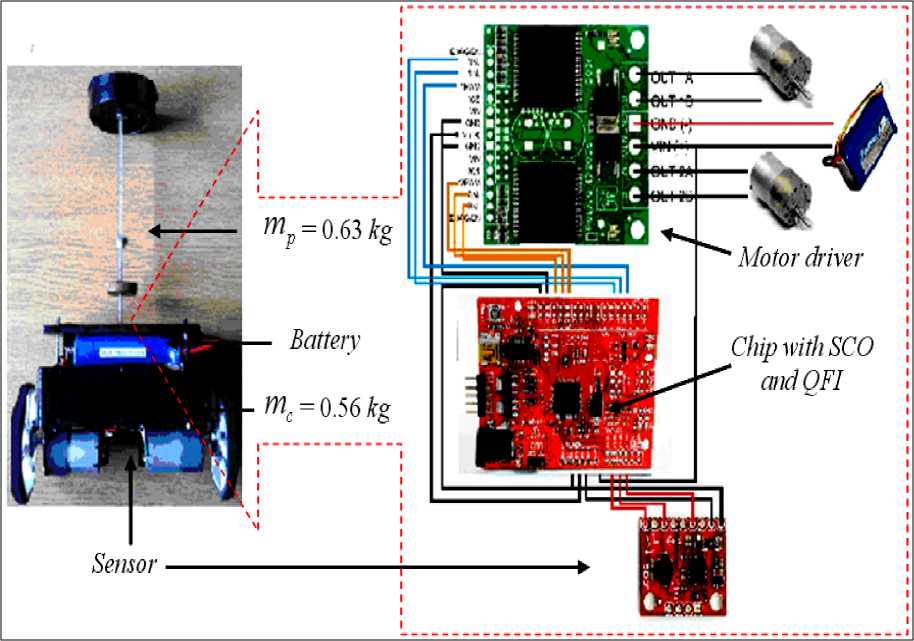
Рис. 7а. Макет робота (слева) и элементы платы управления робота (справа)

Рис. 7б. Стенд для экспериментов на штатные и непредвиденные ситуации

В качестве измерительной системы в роботе используется плата с комбинацией датчиков – гироскопа и акселерометра – 5 DoF (пять степеней свободы) IDG500/ADXL335.

Ядром и центральным элементам системы является микроконтроллер компании Microchip® Сhipkit основанный на процессоре PIC32MX320F128. Плата оборудована USB разъемом, для передачи данных с процессора на компьютер. Интерфейс USB используется при проведении экспериментов для передачи угла отклонения и величины управляющего воздействия. Для данного типа микроконтроллеров были реализованы алгоритмы ПИД-регулятора, ГА – ПИД-регулятора и нечеткого регулятора на основе ОБЗ.

Основные функции программ представлены на рис. 7в., обобщённо их можно записать в псевдо код:

• -    Измерение;

• -    Фильтрация;

• -    Управление;

• -    Подсчет времени (задержка).

Рассмотрим отдельно каждый блок схемы (рис. 7в).

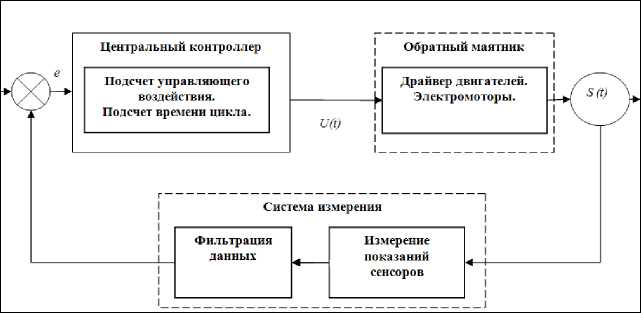
Рис. 7в. Алгоритм программы микроконтроллера

Система измерения считывает данные с датчиков. Количество считываний зависит от скорости работы процессора и чувствительности датчиков. В задаче управления кареткой с перевернутым маятником, важное значение имеет процесс получения достоверных данных о мгновенном состоянии системы. Для повышения точности измерения состояния объекта, полученные данные усредняются:

т

Z 5

,

ActualValue = —— т где т – количество произведенных замеров, S – показания датчиков.

На следующем этапе, происходит нормировка данных. Этот процесс преобразует данные датчиков к единой измерительной системе единиц, воспринимаемой процессором. После этого, данные с гироскопа и акселерометра поступают в фильтр Калмана [12] для получения угла отклонения. На рис. 7г приведен график показаний сенсоров (гироскопа и акселерометра) и величины угла отклонения после фильтрации.

Accel

Accel

0     500   1000   1500  2000   2500   3000   3500  4000   4500

Time

Gyro

-100

0     500   1000   1500  2000   2500   3000   3500  4000   4500

Time

Angle

-100

Angle

0     500   1000   1500  2000   2500   3000   3500  4000   4500

Time

-50

Рис. 7г. Данные получаемые от сенсоров и данные с фильтра Калмана

Используя полученные значения показателей динамики, процессор, в соответствии с алгоритмом, выполняет подсчет управляющего воздействия на основе формулы для ПИД-регулятора (1).

Микроконтроллер использует широтно-импульсную модуляцию (ШИМ-модуляцию), генерируя управляющее воздействие, которое посылается на драйвер двигателей (рис. 7в) для регулирования направления вращения колес и скорости вращения. Исполнительное устройство в данной системе это драйвер двигателей – Dual VNH3SP30 Motor Driver Carrier MD03A совместно с электродвигателями. Схема подключения устройств в роботе представлена на рис. 7а.

Отметим, что данный тип робота на рис. 7а, примеры аналогов [13-20] которого приведены на рис. 8, является типовым Benchmark для тестирования программного инструментария робастного интеллектуального управления.

Рис. 8. Аналоги рассматриваемого на рис. 7а робота

Очевидно, что используя математическую модель можно подобрать коэффициенты для ПИД-регулятора без запуска робота. Следовательно, возможно получить ОС для формирования БЗ в структуре ОБЗ как с математической, так и с физической моделях.

Верификация модели с использованием ГА

Прежде чем приступить к поиску коэффициентов и проектированию ОС, необходимо верифицировать параметры математической модели (5). В таблице 1 представлена классификация определенных и неопределенных параметров.

Проблема поиска недоопределенных параметров может быть решена на основе ГА. Предположительные диапазоны неопределенных параметров являются границами пространства поиска для многокритериальной оптимизации. Хромосома алгоритма состоит из вектора неопределенных параметров, а начальная популяция генерируется случайным способом, разбросом хромосом по пространству поиска.

ГА подбирает набор параметров математической модели так, чтобы динамика работы математической модели соответствует динамике работы робота (ошибка в виде разницы сигналов от математической модели и физического сигнала – минимальна).

Целевая функция алгоритма для верификации основана на дисперсии информации, подаваемой на вход и получаемой на выходе регулятора.

Таблица 1. Определенные и неопределенные параметры

: Хромосома ГА

Определенные		Неопределенные
Масса маятника		Трение в оси
Масса тележки		Коэффициент упругости тележки
Центр тяж ести маятника		Люфт в оси
Ограничения на упр-е воздействие		Коэффициент воздействия (нормирующий)
Время такта системы		Шум измерительной системы
ПИД Коэффициенты		Трение колес о поверхность
Входные и выхо дные данные регулятора технического изделия (2 тыс. точек).

В данной работе, в качестве такой функции пригодности применялась функция вида:

F ( e , u ) =

1 + ( ^Var ( e mod ) - ^Var ( e rob ) ) 2 + ( Var ( ie mod ) - ^Var ⁽ ie rob ) ) 2 + ( ^Var ⁽ u mod ) - ^Var ⁽ u rob ) ) 2 , Var ( e _mod)                  Var ( ie _mod)                   Var ( u _mod)

где, Var ( e _mod) – дисперсия ошибки управления в модели, Var ( e_rob ) – дисперсия ошибки управления в роботе, Var ( u_rob ) и Var ( u_rob ) – дисперсии управляющего воздействия в модели и макете.

После проведения верификации, найденные параметры подставляются в модель, и находим коэффициенты для ПИД-регулятора. Для этого используем ГА, хромосомой которого являются коэффициенты усиления, а функцией пригодности – функция оценки качества управления, например следующего вида:

f (X r ) = -4 --- (8)

• 1    + J e ² dt

где е – величина отклонения от задающего сигнала, t – диапазон интегрирования равен времени проверки одного решения.

Далее коэффициенты тестируются на макете по схеме на рис. 7в.

Примечание . В случае неудовлетворительного результата, следует (если это возможно) уменьшить (увеличить) количество неопределенных параметров путем фиксации одного или нескольких из них в математической модели и увеличением (уменьшением) пространства поиска параметров.

Алгоритм верификации представлен блок-схемой на рис. 9 .

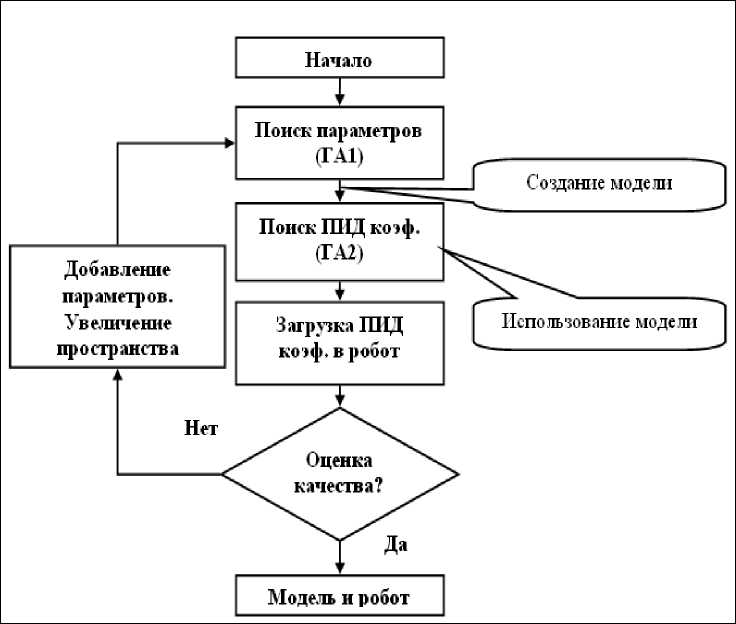
Рис. 9. Алгоритм верификации с использованием ГА

Преимущество генетического алгоритма (ГА), по сравнению с другими методами поиска экстремума, заключается в том, что не требуется вычисления производной от искомой функции. ГА, кроме того, обладает высокой способностью выходить из локальных минимумов. Простота применения ГА и проблемная независимость от вида задачи поиска (т.к. ГА работает с закодированными параметрами), позволяют применять его во многих задачах оптимизации.

Результаты верификации в виде графиков ошибки управления и управляющего воздействия макета и модели представлены на рис. 10 и 11.

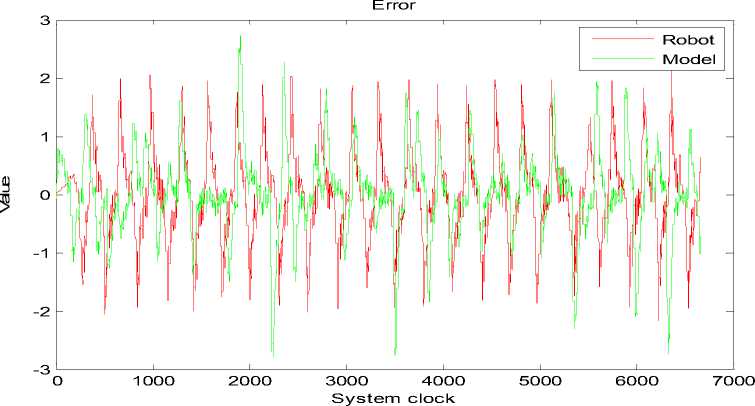
Рис. 10. Угол отклонения макета и модели

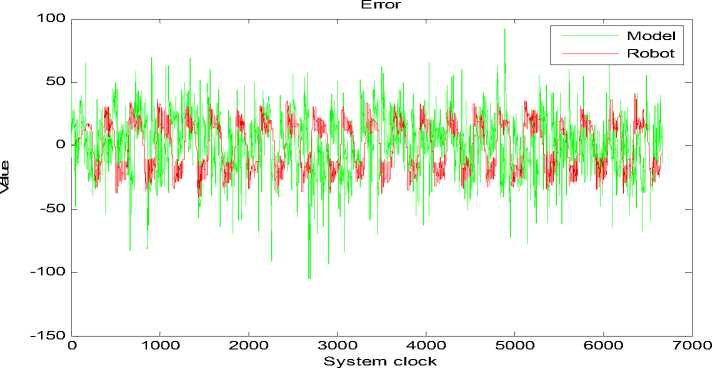
Рис. 11. Управляющее воздействие макета и модели

Сходимость функции пригодности алгоритма осуществлена со следующими значениями: Fit = 0.9847.

В таблице 2 представлены значения дисперсии входного и выходного сигнала ПИД-регулятора, макета и модели:

Таблица 2. Дисперсии входных и выходных данных макета и модели

	Макет	Модель
Дисперсия ошибки управления	0.566	0.511
Управляющее воздействие	336	389

Дополнительно, в таблице 3, представлены критерии позволяющее определить качество верификации. В качестве основного показателя используются разности между графиками:

Таблица 3. Критерии качества верификации

Формулы для вычисления Ошибка управления Управляющее воздействие T robot     mod el 2 J (e   - e ) F (er, em ) = --------T-------- 0,94 694 T robot      model J Ie»     I-\em      1 F(er , em ) = o      T 0,54 10,6 где T – время моделирования с шагом t , etrobot, etmod el – значения ошибки управления или управляю- щего воздействия в момент времени t .

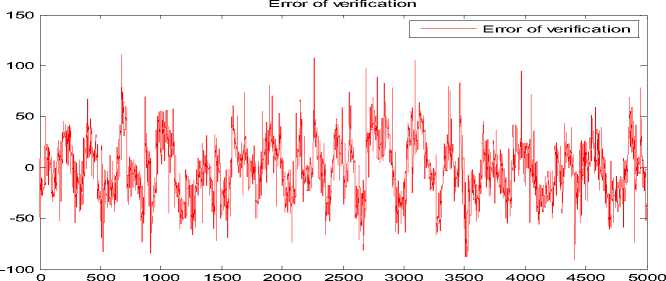
На следующих рис. 12 и 13 представлена в графическом виде разность между ошибкой управления макета и математической модели.

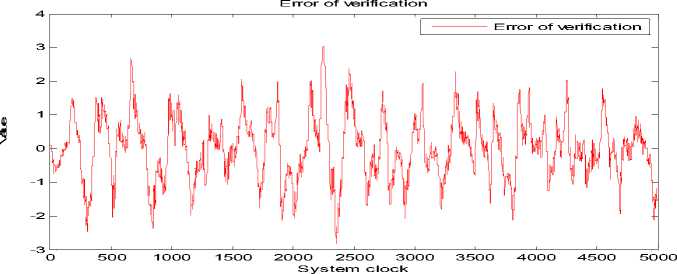
Рис. 12. Разность угла отклонения модели и макета

System clock

Рис. 13. Разность управляющего воздействия макета и модели

На основе верифицированной модели, включающей в себя подобранные не доопределенные параметры ( шум управления, интенсивность шума в управлении, коэффициент трение колес о поверхность, коэффициент трения в оси вращения, коэффициент упругости ) возможно создание БЗ, используя программный инструментарий ОБЗ.

Дальнейшее моделирование проводилось с использованием верифицированной модели.

Применение ГА в режиме реального времени для получения ОС

Создать точную математическую модель для сложной системы на практике достаточно трудно. Настройка такой системы сопровождается огромным количеством экспериментов и множеством сложностей, описанных выше.

Существуют различные способы настройки регуляторов в режиме реального времени. Очевидно, что в САУ добавляется блок настройки или адаптации, способный выполнять функции эксперта. Адаптивные интеллектуальные системы управления в процессе функционирования приспосабливаются к изменениям внешних и внутренних условий, изменяя свои параметры и структуру с целью улучшения качества управления.

В общем виде схема алгоритма САУ с ГА имеет следующий вид (рис. 14):

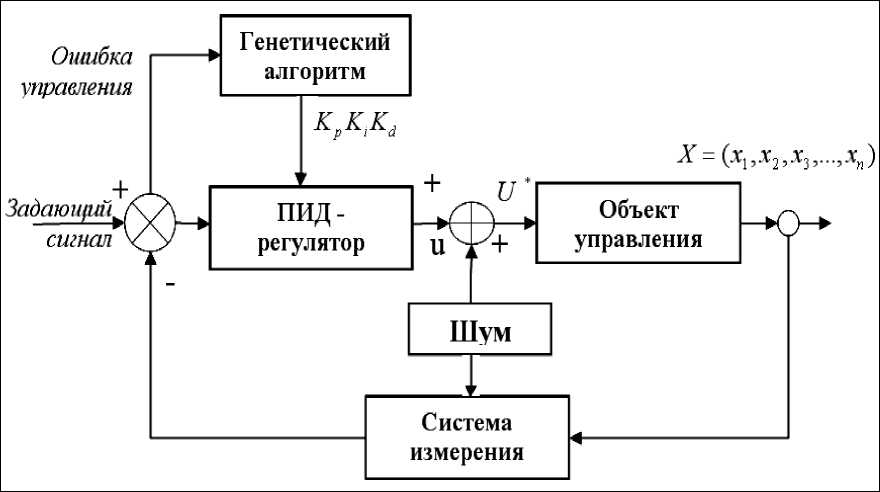
Рис. 14. Блок-схема САУ с системой адаптации

Подобные алгоритмы обычно начинают работу с генерации начальной популяции. Начальная популяция может быть получена случайным образом или путем экспертной оценки из предварительно проведенных экспериментов. Применительно к настройке ПИД-регулятора, каждое решение представляет значения коэффициентов усиления, сложенные в одну хромосому. Так как операции скрещивания и мутации работают с закодированными параметрами, коэффициенты кодируются в бинарную форму с заданной точностью, соответствующей длине бинарной строки. Также определяются диапазоны поиска коэффициентов.

Для поставленной задачи управления был разработан алгоритм управления и определена следующая функция пригодности хромосом – квадрат интегральной ошибки управления:

f ( .V , ) =      ----- .                                                        (9)

• 1 + j e ² dt

В этом случае большим значениям функции пригодности соответствуют малые значения ошибки управления и, следовательно, лучшее качество управления ПИД-регулятора.

Диапазоном интегрирования является период проверки одного решения. Следует уделить особое внимание выбору временного периода оценки решения и выбрать его исходя из динамических и информационных свойств работы контроллера и системы в целом.

Для многокритериальной оценки можно использовать функцию пригодности в виде комплексной величины, состоящей из суммы различных критериев качества работы системы. Например:

fit ( P ) =-------------------- , a + b + c = 1.

1 + ( ae + b I edt + ce ) 2

После каждой итерации робот управляется с использование найденного лучшего решения. Это позволяет ГА продолжать работу, не потеряв управления макетом (рис. 15).

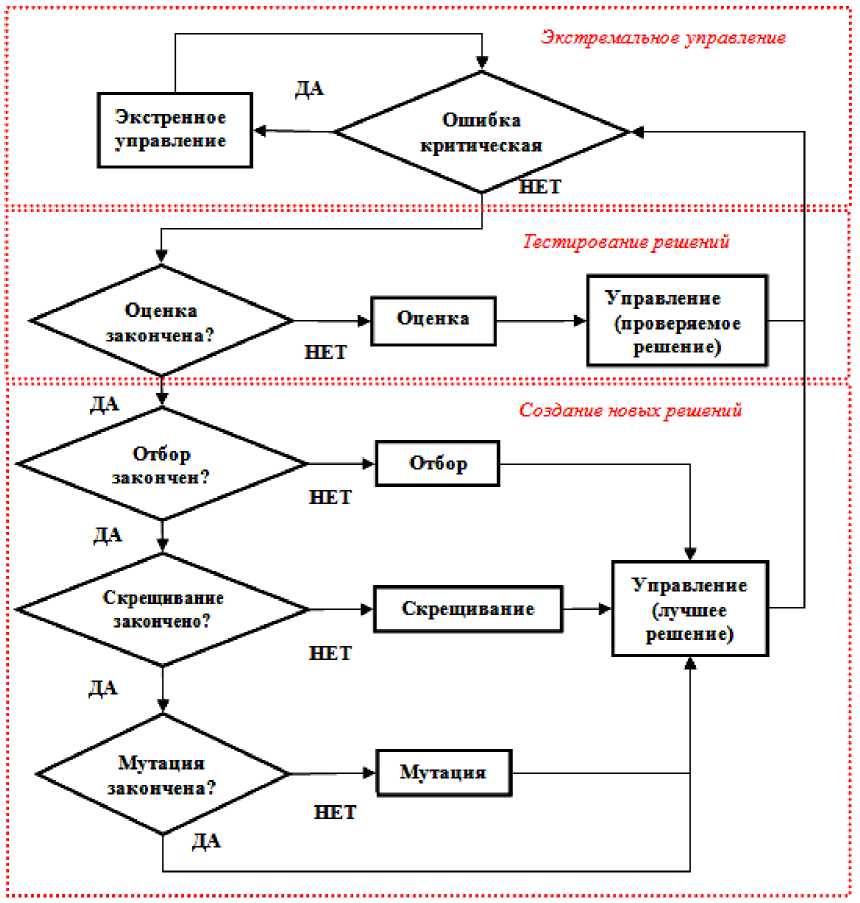
Рис. 15. Алгоритм адаптации ГА – ПИД-регулятора

Введение экстремального управления осуществляется в момент достижения величиной отклонения определенного заранее порога. В моменты работы операторов селекции, скрещивания и мутации, процессорное время занято обработкой данных и нахождением решений, а управляющее воздействие подсчитывается при лучших коэффициентах k_p , k_d , k_i .

Графики изменения коэффициентов такой системы управления представлены на рис. 16 и 17. Подобный алгоритм возможно использовать для настройки ПИД-регулятора в режиме реального времени без использования математической модели.

Kp

00                10                20                30               40                50                60

Time

Kd

Time

Рис. 16. Коэффициенты ГА – ПИД-регулятора в экспериментах с макетом

Рис. 17. Угол отклонения макета ГА – ПИД-регулятора

Такой алгоритм управления не является оптимальным с точки зрения эффективности управления и использования ресурсов контроллера – объема памяти и быстродействия. Полученные экспериментальные результаты показывают, что система управления на основе ГА – ПИД-регулятора уступает в росте интегральной квадратичной ошибки ПИД-регулятору.

Связан этот факт с самим процессом адаптации робота: снижая качество управления, ГА – ПИД-регулятор повышает свою адаптивность.

Рассмотрим возможность применения ГА – ПИД-регулятора для получения ОС и дальнейшей аппроксимации сигнала на нейронной сети с использованием ОБЗ.

Одним из недостатков ГА является невозможность использовать в дальнейшем решения, не попавшие в следующее поколение. При документировании решений, для стороннего наблюдателя работы алгоритма, эти данные превращаются в огромный массив трудно доступной для обработки информации.

Дадим анализ данных, полученных в процессе работы (обучения) ОУ с ГА – ПИД-регулятором в режиме реального времени. На рис. 18а представлен массив данных процесса обучения ОУ и выделены участки «знаний».

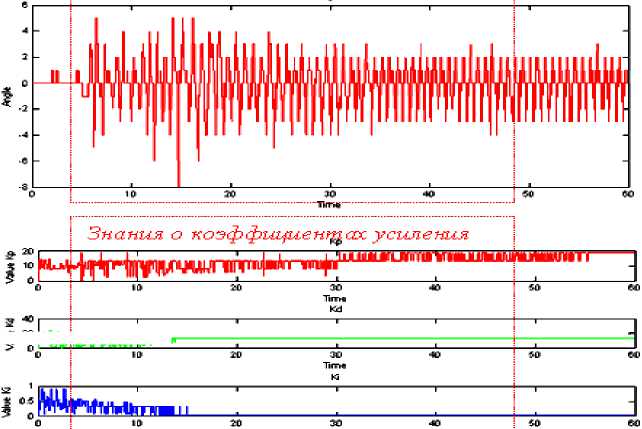
Рис. 18а. ОС с макета

На рис. 18б проиллюстрирована связь между коэффициентами усиления ГА – ПИД-регулятора и НР.

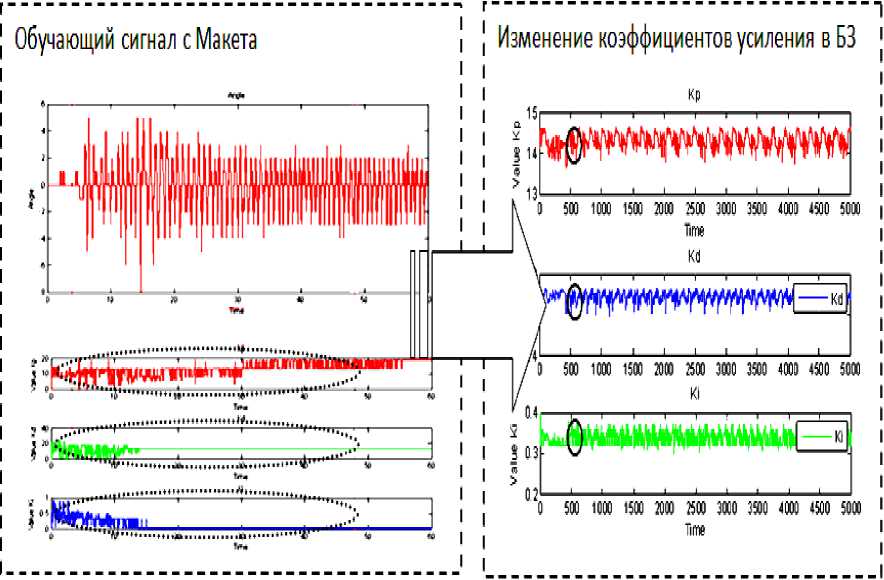
Рис. 18б. Коэффициенты усиления ГА – ПИД-регулятора (обучающий сигнал) и НР

Очевидно, что информация о процессе обучения робота содержит в себе знания (с точки зрения выбранного критерия качества) о пригодности проверяемых решений.

Важно отметить, что количество этих знаний растет в процессе обучения: в первых поколениях (при случайном распределении хромосом по пространству поиска) эти знания минимальны, однако, с течением времени и сменой поколений, количество полезной информации возрастает. В этом массиве данных содержится информация как о возможных состояниях ОУ, так и о коэффициентах усиления для каждого момента времени.

Результаты экспериментов и моделирования показали, что используя программный инструментарий ОБЗ, возможно выделить знания из сигнала, полученного в процессе работы ГА в режиме реального времени, с дальнейшим использованием их в БЗ нечеткого регулятора.

Проектирование БЗ

На рис. 19 представлены основные этапы проектирования БЗ, используя программный продукт ОБЗ.

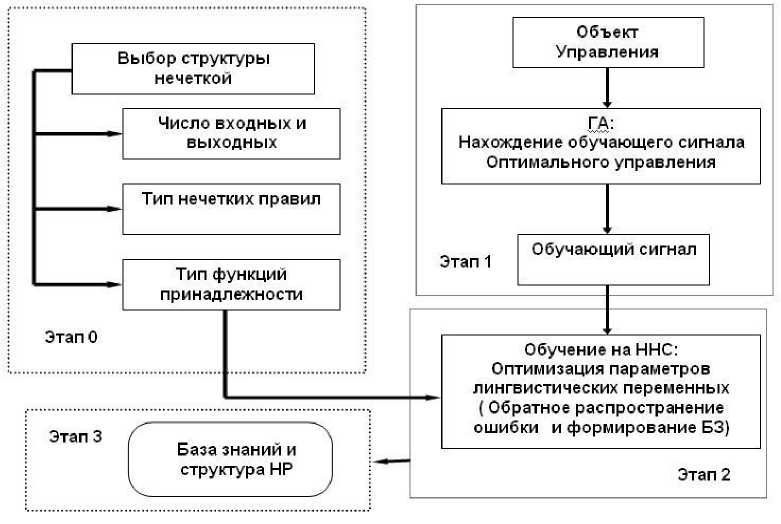
Рис. 19. Основные этапы проектирования БЗ для НР

Перед началом проектирования БЗ необходимо определить структуру БЗ, т.е. необходимо, прежде всего, установить число входных и выходных переменных. Применительно к ПИД-регулятору: 3 входные переменные (ошибки, интеграл ошибки и дифференциал ошибки) и 3 выходных – коэффициенты усиления ПИД-регулятора ( k_p , k_d , k_i ), тип нечетких правил – вид объединения левых частей союзы И/ИЛИ (см. рис. 1).

Тип функций принадлежности в правилах определяется ГА на первом этапе построения БЗ с использованием ОС. В данном случае, в качестве механизма нечеткого вывода, использовался механизм нечеткого вывода Сугено нулевого порядка.

При заданной типовой ситуации с использованием математической модели или реального ОУ, ГА, выбранной функции пригодности (критерия качества) и выбранной области поиска для значений коэффициентов усиления, находим близкое к оптимуму решение ( k_p , k_d , k_i ) в момент времени t .

В данной работе для создания двух БЗ НР использовались два набора параметров для математической модели.

В табл. 4 представлены начальные условия, значения параметров моделей, амплитуды и интенсивности шумов.

Таблица 4. Начальные условия, шумы и не доопределенные параметры модели для получения ОС

	Модель для БЗ 1	Модель для БЗ 2
Начальный угол	30 / -30	30 / -30
Начальная скорость	5 / -5	5 / -5
Коэффициент силы моторов	0.08	0.08
Шум в системе измерения	Амплитуда 0.32, Гауссовский шум, интенсивность 0.01	Амплитуда 0.32, Гауссовский шум, интенсивность 0.01
Шум в системе управления	Равномерный шум [-2.15, 2.15], интенсивность 0.48	Равномерный шум [-2.15, 2.15], интенсивность 0.48
Трение в креплении маятника	3.55	3.55
Трение колес	3.63 + Гауссовский шум 10%	3.63 + Гауссовский шум 20%
Сила упругости	5.54	5.54
Шум в креплении маятника	Нормированный шум с интенсивностью 0.01 и амплитудой 0.35	Гауссовский шум с интенсивностью 0.01 и амплитудой 0.7
Диапазон поиска коэффициентов усиления	15-21	10 - 30
Время и шаг моделирования	Время моделирования 7 при шаге 0.01	Время моделирования 7 при шаге 0.01

Параметры ГА для поиска ОС в программе ОБЗ проиллюстрированы на рис. 20. Также следует отметить установленное время такта системы. Для моделирования и эксперимента значение такта принимались равными и составляют 0.01.

Результатом генетического отбора стал сигнал, часть которого представлена на рис. 21, этот сигнал является входным сигналом в ОБЗ, где первые три столбца – ошибка управления, дифференциальная и интегральная ошибки соответственно, последние три – коэффициенты усиления k_p , k_d , k_i .

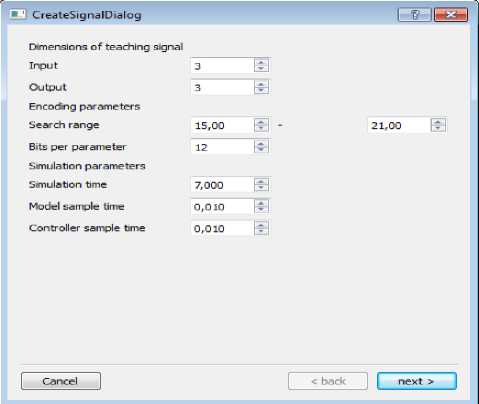
Рис. 20. Окно ОБЗ для установки параметров поиска обучающего сигнала

|-2.9989е+001 2.6002е-001 -3.0113е+001 1.6476е+001 1.9190е+001 1.4440е+001 -2.9239е+001 7.5О12е-ОО1 -б.0102е+001 1.2007е+001 1.О132е+ОО1 7.0293е+000 -2.7578е+001 1.6607е+000 -8.9340е+001 9.ОЗЗОе+ООО 8.7363е+000 1.7912е+001 -2.47б0е+001 2.8181е+000 -1.1692е+002 1.0813е+001 1.52бОе+ОО1 7.1319е+000

Рис. 21. Обучающий сигнал с модели

В виде графика на рис. 22 представлена часть обучающего сигнала – угол отклонения.

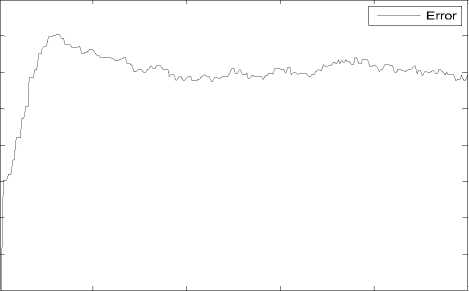
Teaching signal

-5

-10

-15

-20

-25

-30

0           50          100          150          200          250

Time сc

Рис. 22. Ошибка управления в обучающем сигнале угла отклонения маятника

На втором этапе, обучающий сигнал, подается на вход ОБЗ, который аппроксимирует его с помощью заданной пользователем модели нечеткого вывода. С помощью ГА определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности.

Результат этапа построения входных лингвистических переменных представлен на рис. 23-26.

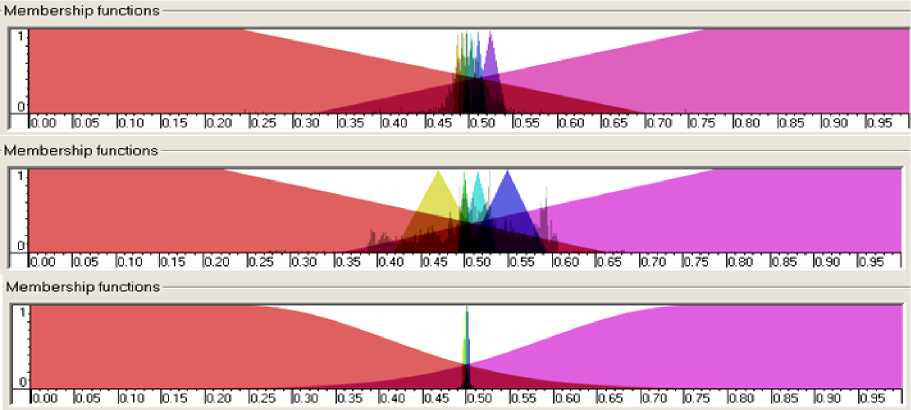
Рис. 23. Функции принадлежности для входных значений. БЗ 1

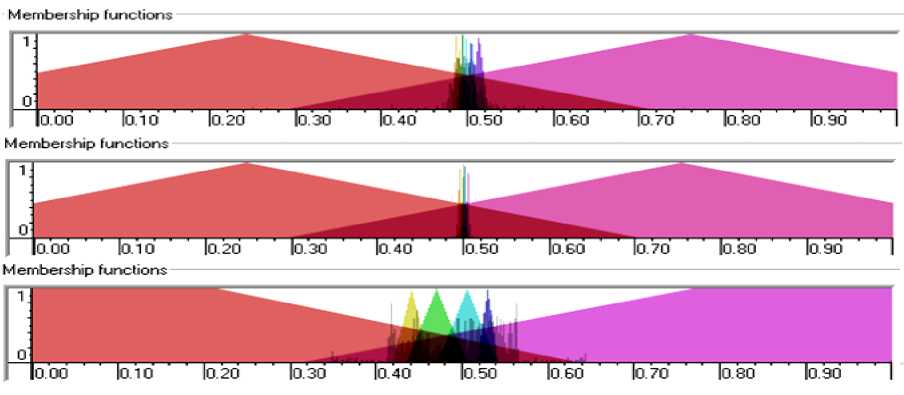
Рис. 24. Функции принадлежности для входных значений. БЗ 2

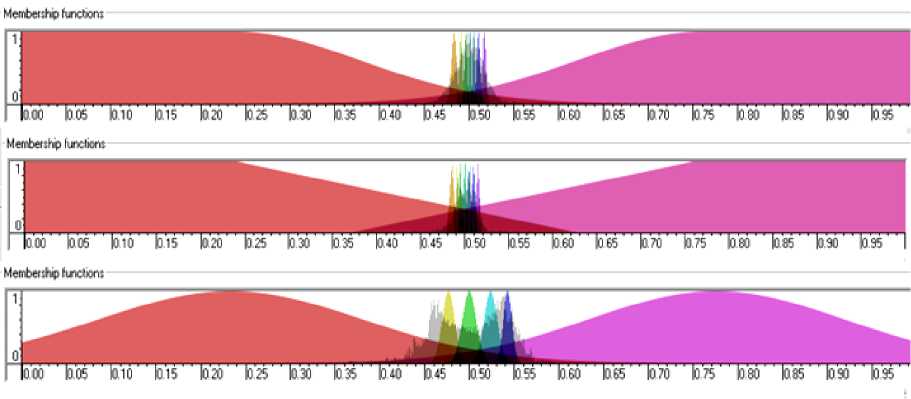
Рис. 25. Функции принадлежности для входных значений. БЗ 3

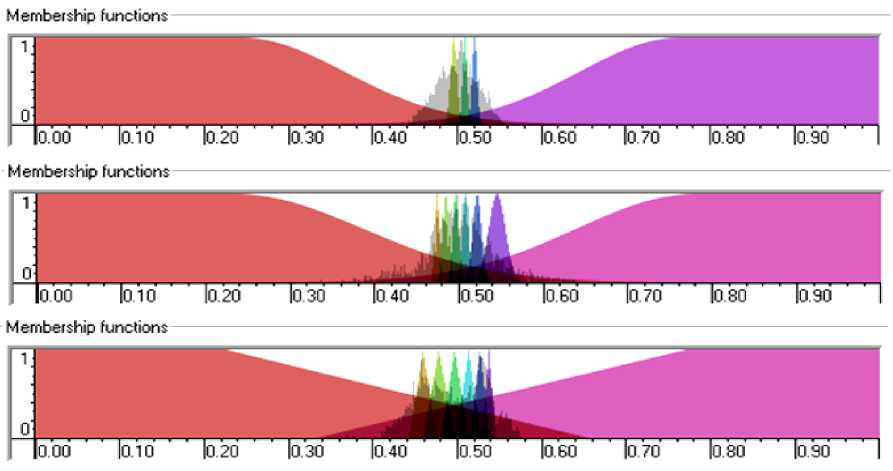
Рис. 26. Функции принадлежности для входных значений. БЗ 4

После формирования левых частей правил, переходим к построению базы правил и получению правых частей БЗ.

На этом этапе правые части правил оптимизировались с использованием ГА2 (для ОС с макета) и МатЛаб модели для ОС, полученных с использованием моделирования.

Результаты построения БЗ иллюстрируются ниже (рис. 27-30а).

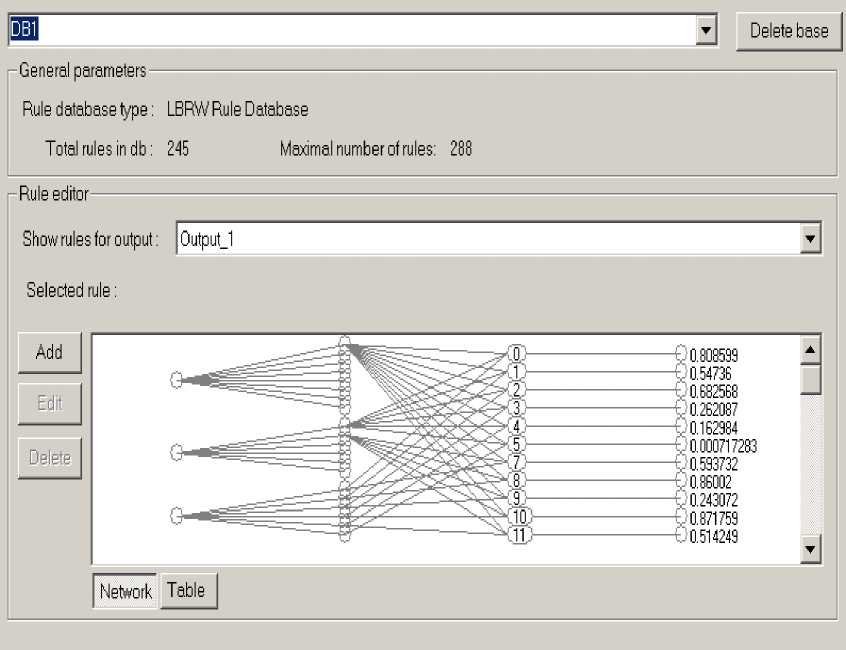
Рис. 27. БЗ 1 (ОС с модели). 245 правил

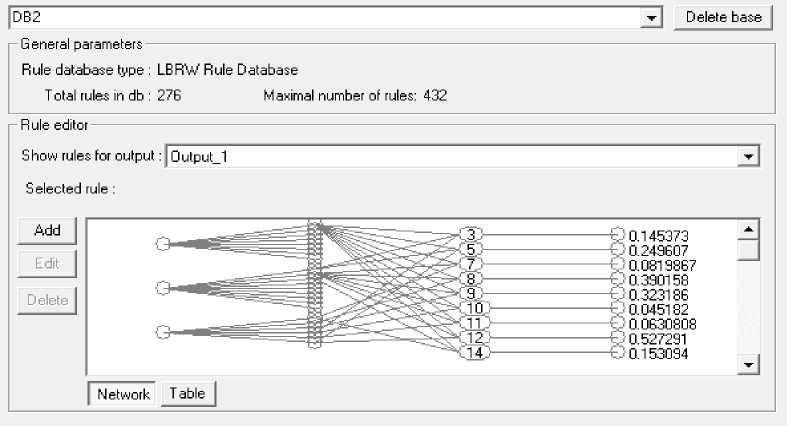
Рис. 28. БЗ 2 (ОС с модели). 276 правил

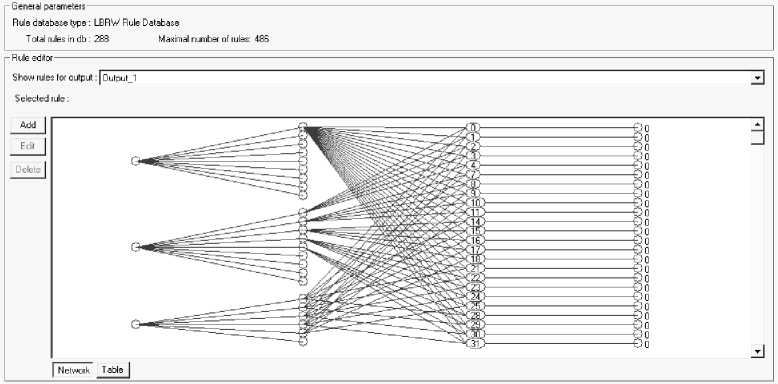
Рис. 29. БЗ 3 (ОС с модели). 288 правил

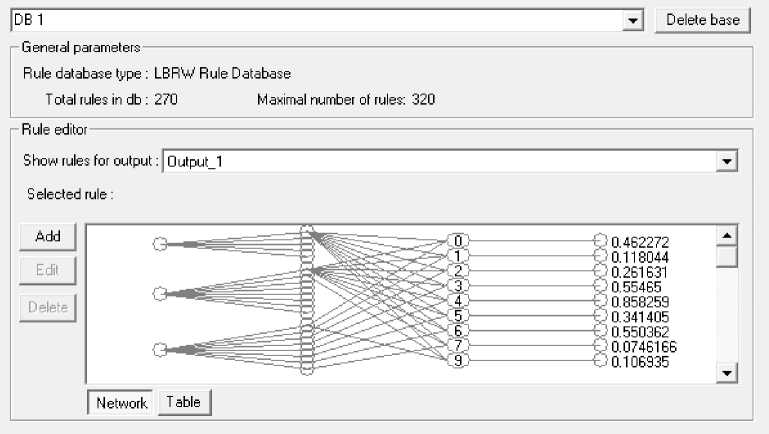
Рис. 30а. БЗ 3 (ОС с модели). 270 правил

Для формирования правых частей правил для БЗ, ОС которых получен с макета, использовался генетический алгоритм (ГА 2 – шаг 4 проектирования БЗ).

Функция пригодности на данном этапе – минимум ошибки аппроксимации ОС. Результат создания и оптимизации правил БЗ представлен в виде нейронной сети (рис. 27-30). Первый слой демонстрирует количество входных переменных, второй – количество функций принадлежности для каждой переменной, третий – продукционные правила БЗ, четвертый – значения коэффициентов усиления.

На рис. 30б. демонстрируется связь между обучающим сигналом полученного с использованием математической модели и коэффициентами усиления нечеткого регулятора.

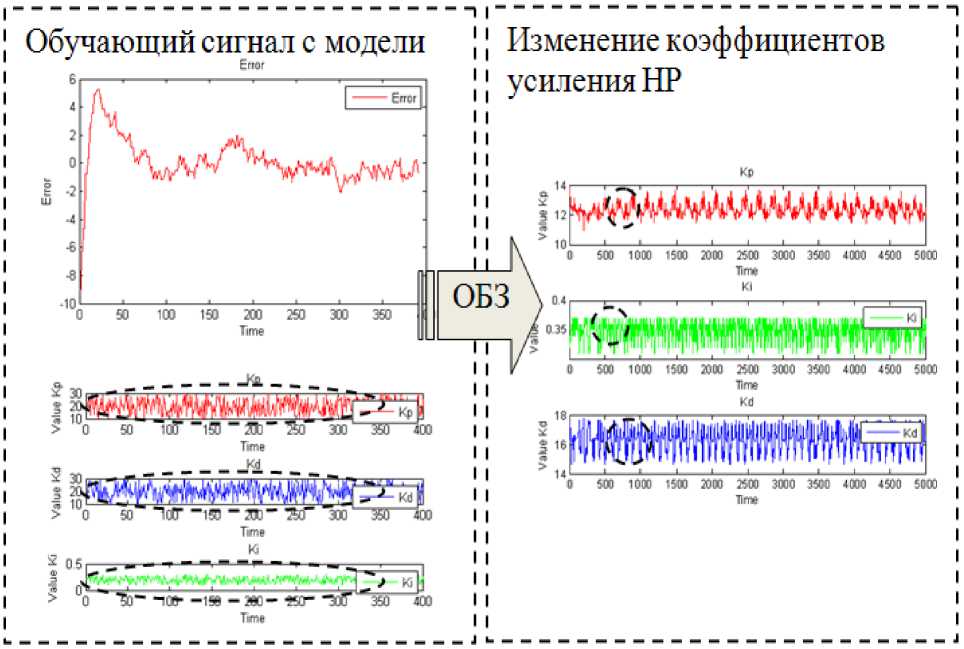
Рис. 30б. Обучающий сигнал с модели и коэффициенты усиления НР

В таблице 5 приведено сравнение БЗ по количеству правил, количеству функций принадлежности лингвистической переменной и способу оптимизации в программном инструментарии ОБЗ.

Таблица 5. Сравнение БЗ.

База №	Количество правил	Кол-во ф-ций принадлежности	Способ оптимизации
База 1 Модель	245	8х6х6	Моделирование
База 2 Модель	276	8х9х6	Моделирование
База 3 Макет	288	9х9х6	Аппроксимация ОС (ГА2)
База 4 Макет	270	5х8х8	Аппроксимация ОС (ГА2)

Моделирование и эксперимент

Исследование качества управления ПИД-регулятора и нечетких регуляторов на основе программного инструментария ОБЗ проводилось с использованием математической модели и реального ОУ. Регуляторы разрабатывались для функционирования в типовой ситуации управления. Параметры математической модели используемой для моделирования представлены в Таблице 6.

Таблица 6. Ситуации управления, параметры математических моделей

	Типовая ситуация (С1)	Непредвиденная (С2)
Начальный угол	0	0
Начальная скорость	1	1
Масса тележки	0.56	0.56
Масса маятника	0.63	0.63
Длинна маятника	0.07	0.07
Трение в креплении	3.55 + нормированный шум с интенсивностью 0.01 и амплитудой 0.35	2.75 + нормированный шум с интенсивностью 0.01 и амплитудой 0.35
Трение колес	3.63 + Гауссовский шум 15%	2.53 + Гауссовский шум 15%
Сила упругости	5.54	7.54
Шум в системе управления	Равномерный [-2.15 2.15], интенсивность 0.48	Равномерный [-2.55 2.55], интенсивность 0.48
Шум в системе измерения	Амплитуда 0.22, Гауссовский шум, интенсивность 0.01	Амплитуда 0.42, Гауссовский шум, интенсивность 0.01
Задержка управляющего воздействия	0.01	0.01

Для сравнения робастности разработанных систем управления используем непредвиденную ситуацию управления. Ситуация моделируется наличием шума в коэффициенте трения колеса о поверхность и в управляющем воздействии. В качестве такого шума в эксперименте используется специальное покрытие, а для моделей были установлены соответствующие значения параметров.

На рис. 31 представлена структура системы моделирования.

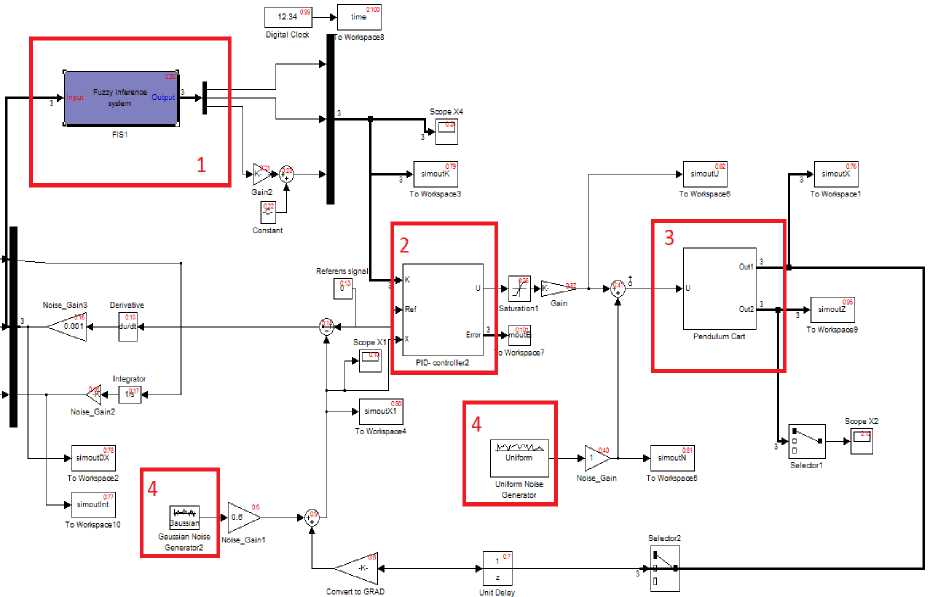
Рис. 31. Структура системы моделирования: 1 - Блок нечеткого вывода; 2 – ПИД-регулятор; 3 - объект управления; 4 - Генераторы шумов

Рассмотрим поведение ПИД и нечетких регуляторов в типичной ситуации управления.

На рис. 32-35 представлены результаты моделирования и экспериментов:

Error

PID

FC1

FC2

FC3

FC4

-1

-2

-3 IIIII---------------------------------!---------------------------------!---------------------------------1

0    100   200   300   400   500   600   700   800   900   1000

Time

Рис. 32. Ошибка управления. Типовая ситуация управления. Моделирование

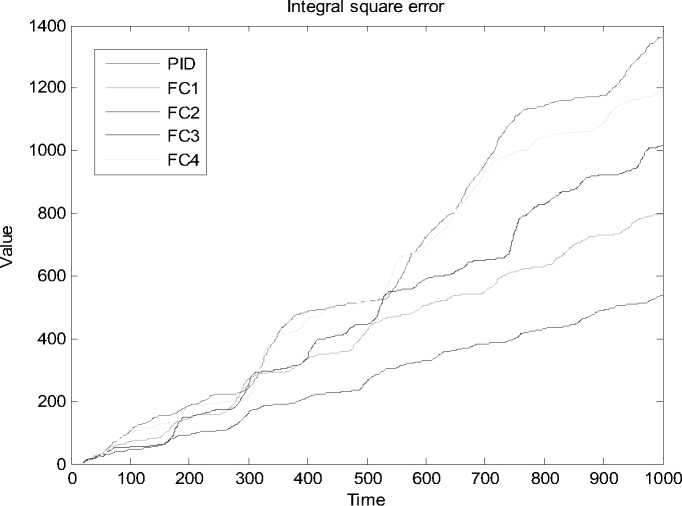
Рис. 33. Интеграл квадратичной ошибки. Типовая ситуация управления. Моделирование

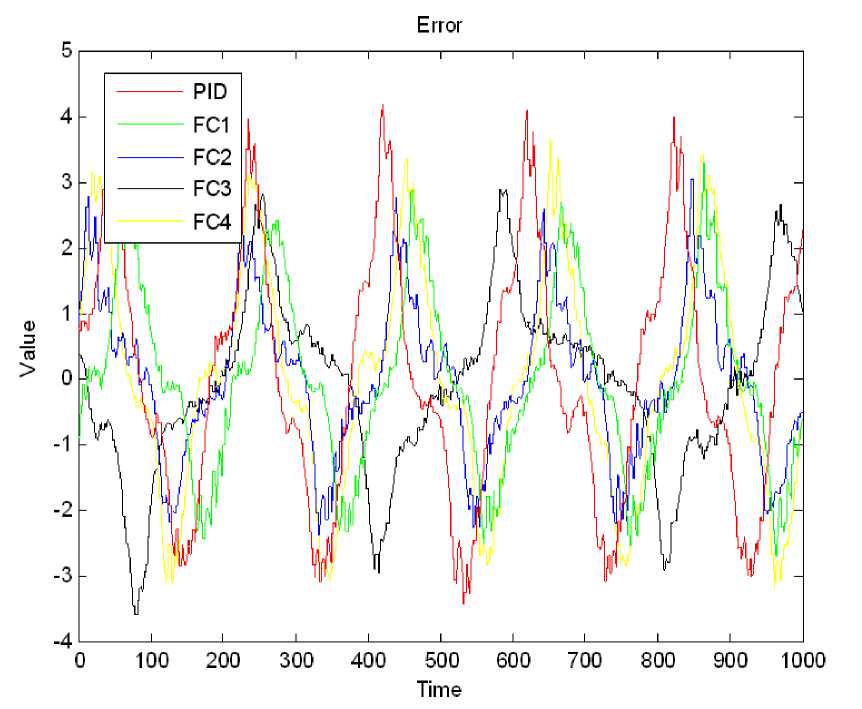
Рис. 34. Ошибка управления. Типовая ситуация управления. Эксперимент

Для оценки качества процесса управления используют показатели переходного процесса (рис. 36). К таким показателям относятся: сложность управления, устойчивость, величина перерегулирования.

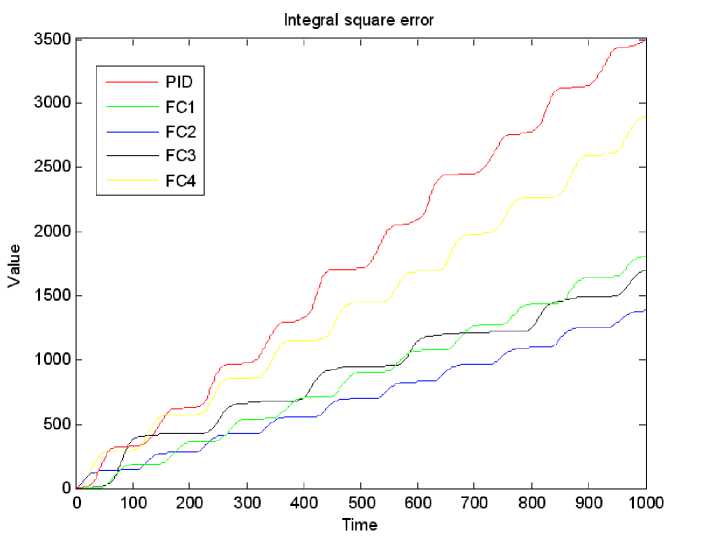
Рис. 35. Интеграл квадратичной ошибки. Типовая ситуация. Эксперимент

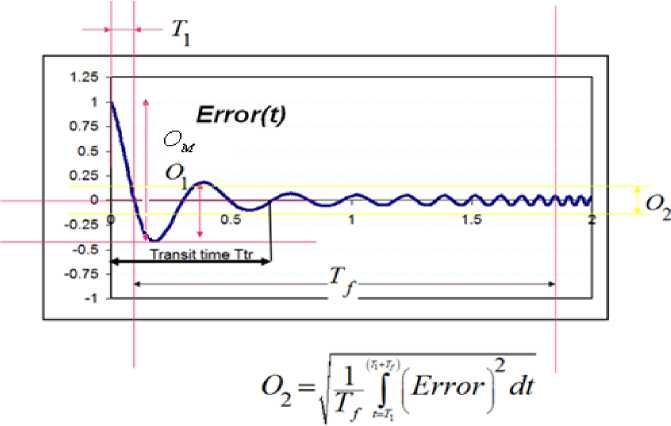
Рис. 36. Показатели качества управления

Перерегулирование характеризует колебательное свойство переходного процесса и рассчитывается согласно (11-13).

На рис. 37 представлена диаграмма уровня перерегулирования систем управления. Нечеткий регулятор, разработанный на основе верифицированной математической модели, имеет более низкий показатель перерегулирования, что характеризует работу такого регулятора как более эффективную:

O i = 1 - O 4 O m ( const .) >  O i .                                  (11)

m

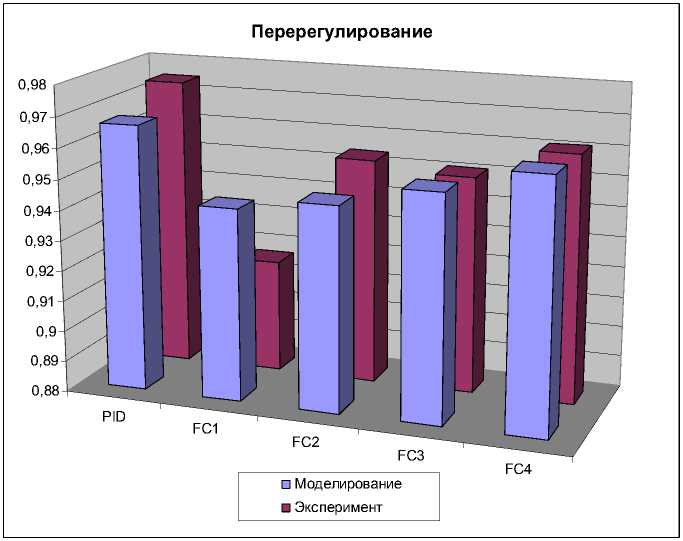
Рис. 37. Перерегулирование систем управления в типовой ситуации. Моделирование и эксперимент

Устойчивость переходного процесса (рис. 38) рассчитывается как:

O ₂ = 1 - —; O_m ( const .) >  O ₂. O m   ^m

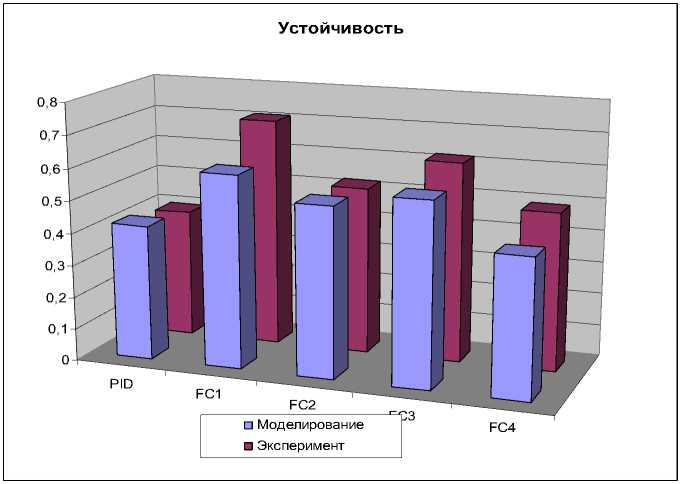
Рис. 38. Устойчивость систем управления в типовой ситуации. Моделирование и эксперимент

Качество управления характеризует способность системы управления эффективно расходовать энергетический и технический ресурс системы. В случаи реализации сложного управления, износ оборудования и затраты энергии будут велики.

Сложность управления (рис. 39) рассчитывается в виде:

P = 1 -

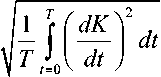
A

; A = ( const ).

Оценка сложности управления показала, что нечеткие регуляторы, разработанные с использованием ОБЗ, обеспечивают систему более простым управлением, что в конечном итоге положительно сказывается на сроке использования оборудования, снижая износ и повышая надежность.

Результаты моделирования и эксперимента в непредвиденной ситуации представлены в графическом виде на рис. 40 и 43. Из графиков (рис. 40 и 43) видно, что ПИД-регулятор не обладает необходимой робастностью, что в непредвиденной ситуации управления приводит потере устойчивости системы.

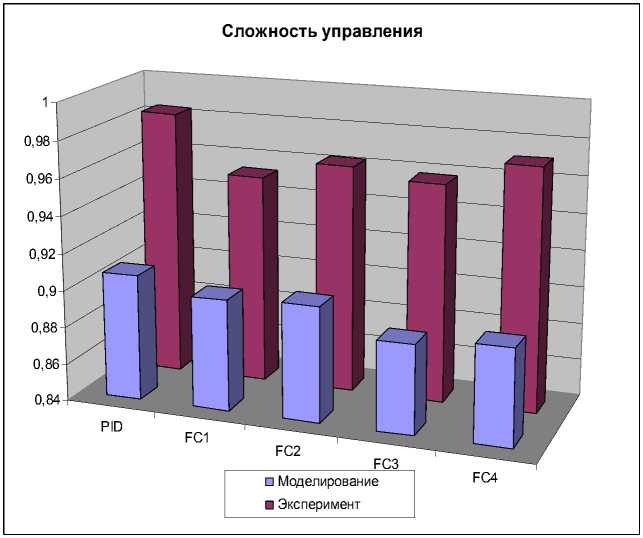
Рис. 39. Сложность управления в типовой ситуации. Моделирование и эксперимент

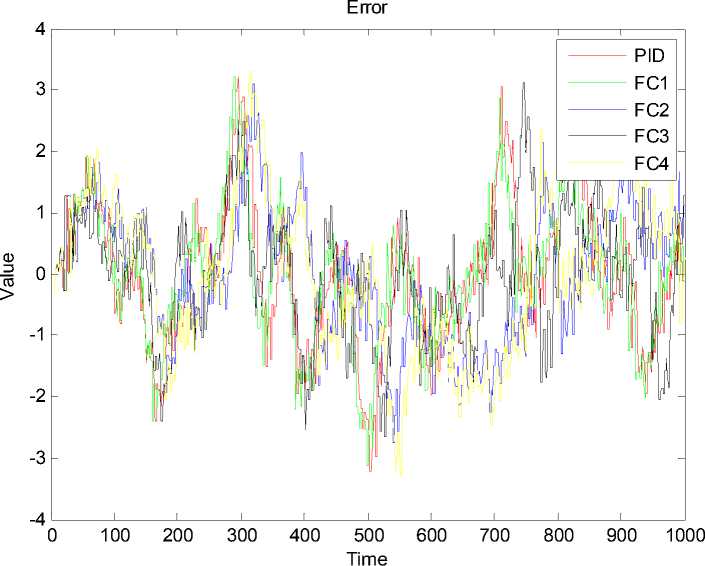
Рис. 40. Ошибка управления. Непредвиденная ситуация. Моделирование

Рис.

Value

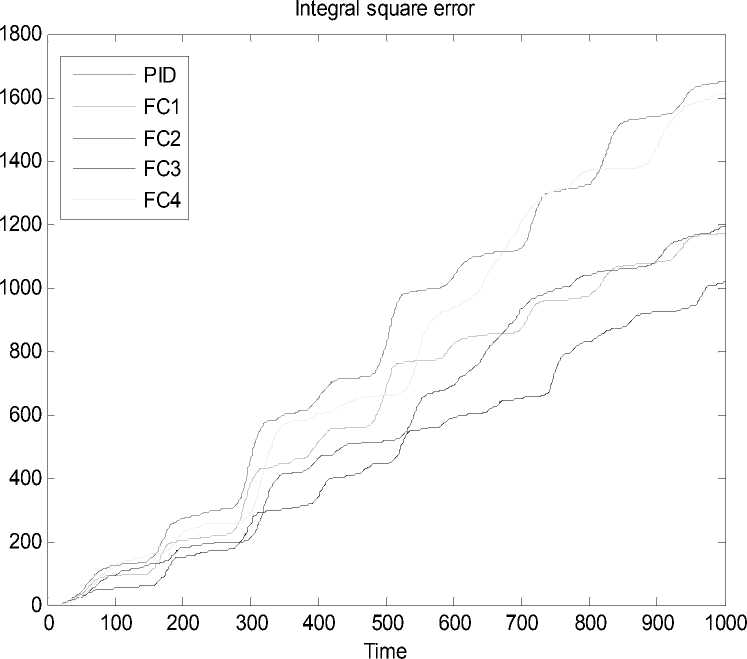
. 41. Интеграл квадратичной ошибки. Непредвиденная ситуация. Моделирование

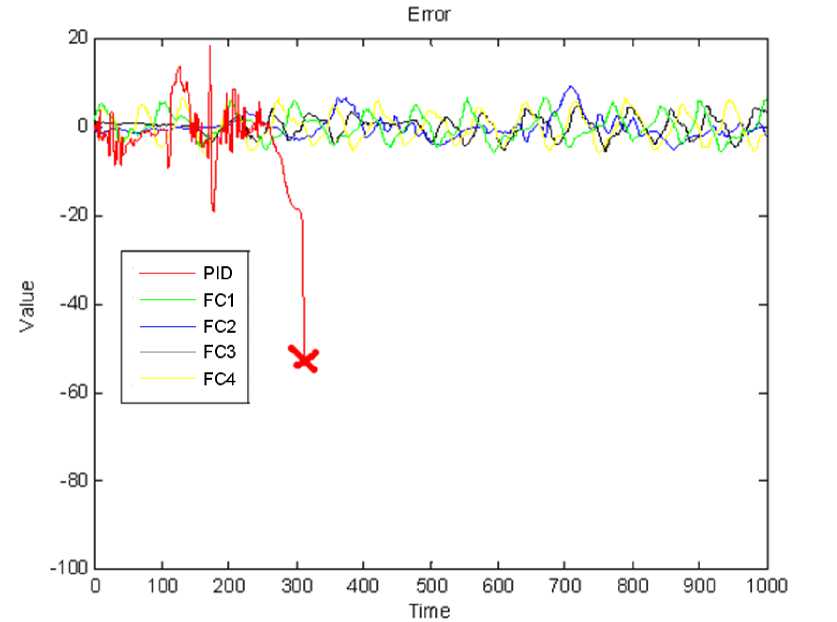
Рис. 42. Угол отклонения робота. Непредвиденная ситуация. Эксперимент

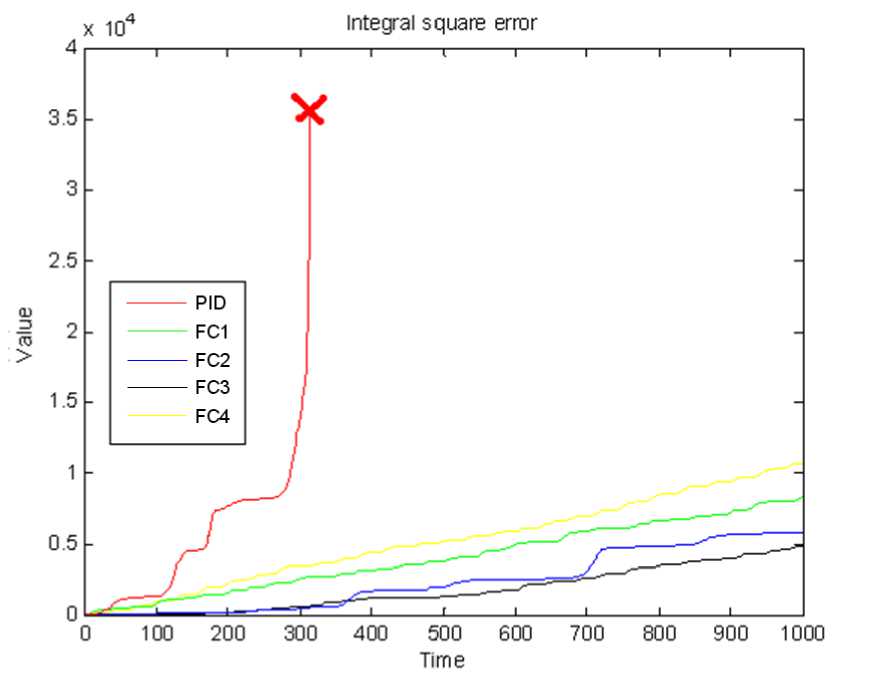
Рис. 43. Интеграл квадратичной ошибки робота. Непредвиденная ситуация. Эксперимент

Высокая эффективность работы нечеткий регулятор (fuzzy controller) FC1 демонстрирует качество проведенной верификации.

Разработанный с использованием математической модели, для типовой ситуации управления, НР1 (FC1) справился с задачей управления лучше всех, что подтверждено результатами моделирования и эксперимента. Данный результат демонстрирует качество метода верификации математической модели с применением ГА.

Смежные работы. Рассмотренный в данной работе автономный робот (рис. 7a) и разработанные в [13-20] и мн. др. его разновидности (рис. 8), являются частным случаем модели одноколесного робота – велосипеда [40-43], которая представлена на рис. 44.

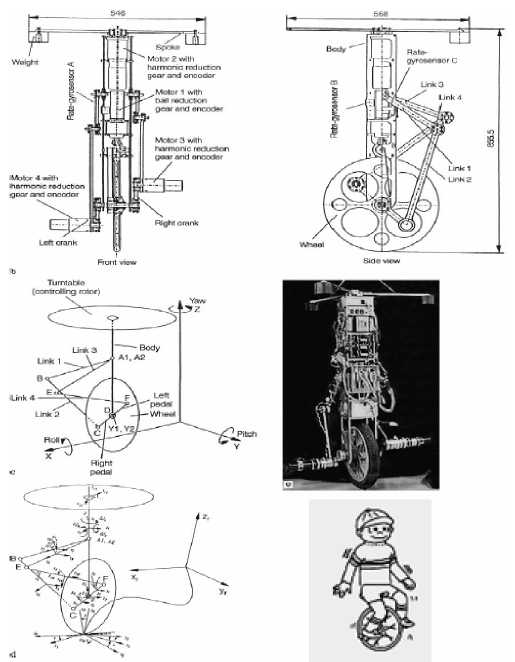
Рис. 44. Одноколесный робот – велосипед

Модель, представленная на рис. 44, описывает био-инспирированную физическую модель. Разработанная методология формирования ОС также применима для такой сложной динамической системы с 39 степенями свободы [44].

Следовательно, формирование ОС с физической модели с последующим этапом верификации недоопределенных параметров математической модели на основе ОБЗ на мягких вычислениях позволяет сформировать редуцированную математическую модель ОУ (робастную модель) без потери количества извлекаемых знаний и качества управления.

В этом случае реализуется принцип компенсации неполноты информационного описания математической модели ОУ за счет интеллектуальных вычислений в виде ОБЗ на мягких вычислениях.

Таким образом, результаты эксперимента показывают, что нечеткие регуляторы, БЗ которых спроектированы по разработанной методологии, обладают повышенной робастностью и способны справляться с задачей управления на широком классе непредвиденных ситуаций.

Выводы

Программный инструментарий разработанной технология проектирования ОБЗ для нечетких регуляторов ИСУ включает в себя:

• -    многокритериальный ГА для поиска оптимального управления и верификации,

• -    нечеткую нейронную сеть для аппроксимации найденного с помощью ГА оптимального сигнала управления и извлечение на его основе «оптимальной» БЗ,

• -    «тонкую» настройку БЗ на основе ГА с использованием информационно-энтропийных критериев.

ОБЗ позволяет осуществить принцип проектирования оптимальной ИСУ с максимальным уровнем надежности и управляемости сложным ОУ в условиях неопределенности исходной информации.

Применение БЗ, спроектированных с помощью ОБЗ, в структуре ИСУ расширяет область промышленных приложений САУ сложным динамическим ОУ.

Адекватность верификации подтверждается разработанным нечетким регулятором, способным справляться с задачей управления в непредвиденной ситуации управления.

Описанный метод получения обучающего сигнала с использованием ГА в режиме реального времени позволяет проектировать БЗ нечетких регуляторов, в отличии от методологий многих работ [21-39] и др., без использования математической модели.

Данные БЗ проявляют высокий уровень робастности.