Метод эквивалентных условий прочности в расчетах композитных конструкций регулярной структуры с применением многосеточных конечных элементов

Введение. Расчет на прочность конструкции – один из важнейших на этапе эскизного проектирования [1], которое является технико-экономическим обоснованием проекта конструкции. Как правило, расчет на прочность конструкций проводится по запасам прочности [1–3]. Согласно этому расчету, для коэффициента запаса n ₀ проектируемой конструкции V ₀ заданные условия прочности имеют вид n ₁ ≤ n ₀ ≤ n ₂,                     (1)

где n ₁, n ₂ – заданы, n ₁ >  1 .

На этапе эскизного проектирования конструктору в первую очередь важно знать, удовлетворяет или не удовлетворяет коэффициент запаса n0 проектируемой конструкции V0 заданным условиям прочности (1). Если коэффициент n0 удовлетворяет заданным условиям прочности, то считают, что конструкция V0 не разрушается при заданных условиях эксплуатации. Следует отметить, что в этом случае нет необходимости детально исследовать напряженно-деформированное состояние (НДС) конструкции V0 . Расчет на прочность конструкции V0 сводится к нахождению ее коэффициента запаса n0 и проверке условий прочности (1) для коэффициента n0 . Коэффициент запаса n0 определяют по формуле n0= σT / σ0 [1–3], где σT – предельное напряжение конструкции V0 (предел текучести [3]), σ0 – максимальное эквивалентное напряжение конструкции V0 . Отметим, что коэффициент запаса n0 отвечает точному решению задачи упругости, сформулированной для конструкции V0 . Если максимальные эквивалентные напряжения конструкций определяются приближенно, то в этом случае используются скорректированные условия проч- ности [4]. При анализе НДС композитных конструкций широко используют метод конечных элементов (МКЭ) [5–8]. Базовые дискретные модели конструкций с неоднородной и микронеоднородной структурой, которые состоят из конечных элементов (КЭ) 1-го порядка и учитывают их структуры в рамках микроподхода [9], имеют очень высокую размерность, что порождает трудности при реализации МКЭ на ЭВМ. Для таких моделей эффективно используется метод многосеточных конечных элементов (ММКЭ) [10–12], в котором используются многосеточные конечные элементы (МнКЭ) [13; 14]. Следует отметить, МКЭ есть частный случай ММКЭ, и если при решении краевых задач по МКЭ используются МнКЭ, то в этом случае, по сути, реализуется ММКЭ.

Для практики важно знать погрешность приближенного решения, которое используется в расчетах. Оценить погрешность приближенных решений можно тогда, когда они мало отличаются друг от друга и при этом образуют последовательность решений, которая быстро сходится к точному решению. При построении таких последовательностей применяется процедура измельчения исходного разбиения области тела на КЭ. Процедуры измельчения, используемые для разбиений, которые построены для неоднородной и микронеоднородной (волокнистой) структуры, сложные и труднореализуемы. Так как волокна имеют малую толщину, то измельчение таких разбиений приводит к резкому увеличению размерностей дискретных моделей. Реализация МКЭ для таких моделей требует больших ресурсов ЭВМ. Кроме того, на закон измельчения накладываются определенные ограничения, связанные с тем, что на каждом шаге измельчения разбиений необходимо учитывать микронеодно-родную структуру по микроподходу. Как известно, процедура измельчения, применяемая для дискретных моделей однородных изотропных тел, наиболее простая в реализации и требует меньше памяти ЭВМ, чем для тел с неоднородной и микронеоднородной структурой (с учетом их структуры).

В данной работе предложен метод эквивалентных условий прочности (МЭУП) для статического расчета на прочность линейно упругой конструкции V₀ с неоднородной (микронеоднородной) регулярной структурой, состоящей из пластичных материалов. Для простоты изложения считаем, что тело V ₀ имеет волокнистую структуру. Показано, что расчет на прочность композитного тела V ₀ сводится к расчету на прочность (с помощью МКЭ) изотропного однородного тела V b . Тела V ₀, V b имеют одинаковые форму, размеры, закрепление и нагружение. Модули упругости тела V b и волокна совпадают. В расчетах приме -няются скорректированные эквивалентные условия прочности вида

Pn 1⁽¹ +6 1 ) <  n b <  Pn 2 ⁽¹ -6 2 ), ⁽²⁾ где 6 1 = 1/(1 - 8 _p ) - 1, 6 ₂ = 1 - 1/(1 + 8 _p ); p - коэффициент эквивалентности; n b - коэффициент запаса тела V b , n b = ст T / ст ^b ; ст T - предел текучести волокна; ст ^b - максимальное эквивалентное напряжение тела V b (определяемое с помощью МКЭ); 8 _p - погрешность для напряжения ст ^b , 0 <8 _p <  1.

Показано, что если коэффициент запаса n_b изотропного однородного тела V b удовлетворяет скорректированным эквивалентным условиям прочности (2), то коэффициент запаса n ₀ композитного тела V ₀ (отвечающий точному решению задачи упругости) удовлетворяет заданным условиям прочности (1). Таким образом, реализация предлагаемого метода сводится к построению скорректированных эквивалентных условий прочности (2) и нахождению коэффициента запаса n b тела V^b , т. е. к определению коэффициента эквивалентности p и к нахождению с помощью МКЭ максимального эквивалентного напряжения ст ^b для тела V b (с погрешностью 8 _p ). Коэффициент эквивалентности p находим по формуле p = ст ₀ / ст ^b , где ст ₀ - максимальное эквивалентное напряжение тела V ₀. Напряжения ст ₀ для композитного тела V ₀ и ст ^b для изотропного однородного тела V^b определяем по МКЭ (с применением МнКЭ). Для построения оценки погрешности приближенных решений используются последовательности решений, полученные с помощью МКЭ, которые быстро сходятся к точным.

Достоинства МЭУП состоят в следующем. В расчетах используем изотропные однородные конструкции, которые имеют такие же формы и размеры, закрепления и нагружения, как композитные конструкции. При анализе НДС изотропных однородных конструкций по МКЭ применяются МнКЭ, которые позволяют строить последовательности решений бы-стросходящиеся к точным, что позволяет определить погрешность для полученных приближенных решений. МнКЭ для изотропных однородных конструкций порождают дискретные модели малой размерности и приближенные решения с малой погрешностью. Реализация МКЭ для многосеточных дискретных моделей требует в 103 ^ 106 раз меньше объема памяти ЭВМ, чем для базовых. При реализации МЭУП не используются процедуры измельчения дискретных моделей композитных конструкций. Приведен пример расчета на прочность балки с микронеодно-родной регулярной волокнистой структурой с помощью МЭУП.

Основные положения для конструкций. В работе рассматриваются трехмерные конструкции (тела), для которых выполняются следующие условия.

Положение 1. Рассматриваются в декартовых системах координат трехмерные линейно упругие изотропные однородные и композитные тела (конструкции), которые состоят из пластичных материалов, имеют гладкие границы, статические нагружения и одинаковые условия эксплуатации. Функции нагружений тел являются гладкими функциями. Тела имеют границы закрепления, которые не вырождаются в точки. Композитные тела состоят из разномодульных изотропных однородных тел, связи между которыми идеальны, т. е. на общих границах разномодульных однородных тел функции перемещений и напряжений являются непрерывными. Перемещения, деформации и напряжения разномодульных тел отвечают соотношениям Коши и закону Гука трехмерной линейной задачи теории упругости [15]. Эквивалентные напряжения для упругих тел определяются по 4-й теории прочности [1].

Эквивалентные условия прочности и эквивалентные по прочности конструкции, выраженные через коэффициенты запаса. Пусть две упругие конструкции V1 и V2 имеют одинаковые форму, геометрические размеры, закрепления и статические нагружения, но отличаются модулями упругости. Пусть для коэффициентов запаса n1 , n2 соответственно конструкций V1 , V2 заданы условия прочности na < n1 < nb,                       (3)

n ² <  ⁿ 2 <  n b ²,                      (4)

где n a , n 2 >  1; n a , n 2 , n b , n b - заданы, коэффициент n ₁ ( n ₂ ) отвечает точному решению задачи упругости, сформулированной для конструкции V ( V ₂).

Для конструкций V ₁ , V ₂ введем следующие два определения.

Определение 1. Если из выполнения условий (4) для коэффициента n2 следует выполнение условий (3) для коэффициента n1 и наоборот, если из выполнения условий (3) для коэффициента n1 следует выполнение условий (4) для коэффициента n2 , тогда условия прочности (3), (4) будем называть эквива- лентными условиями прочности соответственно для конструкций V, V2.

Определение 2. Пусть конструкции V₁, V₂, для которых соответственно условия (3), (4) являются эквивалентными условиями прочности, не разрушаются при одинаковых условиях эксплуатации. Тогда конструкции V₁ , V₂ будем называть эквивалентными по прочности.

На практике эквивалентность по прочности конструкций V , V ₂ означает, что вместо работающей конструкции V можно использовать конструкцию V , , и наоборот. Отметим, что из двух эквивалентных по прочности конструкций целесообразно использовать в работе такую конструкцию, которая более технологична в изготовлении, отвечает заданным техническим требованиям и требует меньше финансовых затрат на изготовление и эксплуатацию.

Теорема о существовании эквивалентных условий прочности. Рассмотрим теорему, в которой доказывается существование эквивалентных условий прочности для упругих композитных конструкций (тел).

Теорема 1. Пусть на трехмерное линейно упругое композитное тело V0 (расположенное в декартовой системе координат Oxyz) действуют заданные статические поверхностные силы q, т. е. силы, действующие на незакрепленной части границы Sq тела V, и объемные силы p, где q = {qx, qy, qz}T , p ={Px, Py, Pz}T: qx, qy, qz, Px, Py, Pz - гладкие функции координат x, y , z . На границе Su тело V0 жестко закреплено, т. е. на Su: u = v = w = 0 , S0 = Su + Sq, S0 — гладкая граница тела V0. Тело V0 состоит из компонент Vi, т. е. из пластичных разномодульных изотропных однородных тел Vi , где i = 1,...,N, N- общее число тел Vi тела V0. Пусть максимальное эквивалентное напряжение композитного тела V0 возникает в теле Va, 1 < a < N. Пусть для коэффициента запаса n0 композитного тела V0 (который отвечает точному решению задачи упругости для тела V0) заданы условия прочности ni < n0 < n2 , (5)

где n ₁, n ₂ - заданы, n ₁ >  1.

Тогда существуют такое трехмерное упругое изотропное однородное тело V b и такие числа n ” , n₂ , что если коэффициент запаса n 0 тела V b , отвечающий точному решению задачи упругости для тела V b , удовлетворяет эквивалентным условиям прочности вида

« Т <  n b <  n P , (6)

то коэффициент запаса n ₀ композитного тела V ₀ удовлетворяет условиям прочности (5), и наоборот.

Если коэффициента запаса n ₀ композитного тела V , удовлетворяет условиям (5), то коэффициент запаса n_b ⁰ изотропного однородного тела V^b удовлетворяет условиям (6), причем, между коэффициентами запаса n ₀, n b существует взаимно однозначная связь.

Доказательство. Пусть однородное изотропное тело V^b и композитное тело V ₀ имеют одинаковые форму, размеры, закрепления и нагружения, но отличаются модулями упругости. Пусть модули упругости тела V^b равны модулям упругости тела V _a композитного тела V ₀, 1 < a <  N . Коэффициенты запаса n ₀, n 0 находим по формулам (1-3)

ⁿ 0 = ^о t / ^о 0 ,                    ⁽⁷⁾

n b = о t / о 0 ,                    (8)

где о T - предел текучести тела V _a [3]; о ₀, о ° - максимальные эквивалентные напряжения, возникающие соответственно в телах V ₀ , V^b и отвечающие точным решениям задач упругости.

Пусть коэффициент n0 удовлетворяет условиям прочности (5). Тогда подставляя (7) в (5) получим неравенства n1 < — < n2 .

о 0

Существует такое число P (коэффициент эквивалентности), что

P = °0/о0-

Учитывая (10) в (9), имеем

Pn1 <^7 < Pn 2.

^о b

Используя (8) в (11), получаем

Pn1 < nb < Pn2.

Существуют такие числа n1P , n2P , что nP = Pn1, n” = Pn2.

Подставляя (13) в (12), получаем, что для коэффициента n b выполняются условия (6). Итак, существуют такие числа n ₁ ^P , n ₂ ^P , что коэффициент запаса n_b ⁰ изотропного однородного тела V^b удовлетворяет условиям (6). Обратно, пусть коэффициент запаса n b тела V b удовлетворяет условиям прочности (6). Подставляя (8) в (6) и учитывая (10), (13), получим

, PСТ /

Pn <   <  Pn 2 .

° 0

Откуда с учетом (7) следует выполнение для коэффициента запаса n0 композитного тела V0 условий прочности (5). Итак, показано, что всякому коэффициенту nb е (n1P, n2) соответствует единственный ко- эффициент n0 е (n1,n2), найденный по формуле (7), и наоборот, всякому коэффициенту n0 е (n1, n2) соответствует единственный коэффициент nb е (np, n2), отвечающий формуле (8). Рассмотрим предельные случаи. Пусть n0 = np . Используя соотношения (8), (13), (10) в последнем равенстве, получаем pа T / а0 = pn1. Откуда с учетом (7) следует n0 = n1. Аналогично можно показать, что если nb = n2, то n0 = n2. Пусть n0 = n1. Используя (7), (10) в последнем равенстве, получаем аT / а0 = pn1. Откуда с учетом (8), (13) вытекает nb = nf . Аналогично можно показать, что если n0 = n2, то n0 = n2 . Таким образом, между коэффициентами запаса n0 и nb0 существует взаимно однозначная связь. Теорема 1 доказана.

Эквивалентные условия прочности (6) можно представить через коэффициент эквивалентности p в виде pn 1 <  n b <  pn ₂, построение которых сводится к нахождению коэффициента p .

Отметим, что условия (5), (6) являются эквивалентными условиями прочности соответственно для тел (конструкций) V ₀ , V^b (см. определение 1). Считают, что если n ₀ удовлетворяет заданным условиям прочности (5), то конструкция V ₀ не разрушается при эксплуатации. Пусть конструкция V^b не разрушается при эксплуатации. Тогда конструкции V ₀ , V^b являются эквивалентными по прочности (см. определение 2).

Итак, доказано существование эквивалентных условий прочности для композитных тел (конструкций), имеющих любую структуру, форму, любые размеры, статические нагружения и закрепления, которые отвечают выше сформулированым положению 1 и условиям теоремы 1. Следует отметить, что для всякой композитной конструкции V ₀ всегда можно построить изотропную однородную конструкцию V^b , т. е. всегда для конструкции V^b можно задать по определенным правилам форму, размеры, нагружение, закрепление и модули упругости. Однако, в общем случае, эквивалентные условия прочности для изотропной однородной конструкции V^b можно построить лишь только для заданных усилий q , p , что непрактично. Это связано с тем, что напряжения а ₀, а 0 и p отвечают заданному нагружению q , p конструкций V^b , V ₀ (см. формулы (10), (13)).

Замечание 1. Пусть найдено значение p и максимальное эквивалентное напряжение а0 конструкции Vb . Тогда для конструкции V0 по формуле (10) определяем максимальное эквивалентное напряжение а0, т. е. а0 = pа0, и затем по формуле (7) вычисляем ко эффициент запаса прочности n0, т. е. n0 = аT /(pа0), что важно знать при проектировании конструкции V0 .

Скорректированные условия прочности, учитывающие погрешность напряжений. В общем случае (например, для тел сложной формы) построить аналитические решения трехмерной задачи теории упругости очень трудно. Однако с помощью МКЭ [5–8] и ММКЭ [10–12] можно построить приближенные решения задач теории упругости с заданной погрешностью для напряжений. Следует отметить, что при проектировании ряда конструкций (например, конструкций минимального веса) нарушение заданных условий прочности (5), т. е. эквивалентных условий прочности (6), недопустимо. Эквивалентные условия прочности (6) не учитывают погрешность приближенных решений, что порождает трудности при их выполнении.

Пусть для коэффициента запаса упругой конструкции Vb заданы условия прочности вида np < nb < np ,                 (14)

где n ₁ ^p , n ₂ ^p – заданы; n_b ⁰ – коэффициент запаса прочности конструкции V^b , отвечающий точному решению трехмерной задачи упругости, сформулированной для данной конструкции.

В теореме 2 сформулированы скорректированные условия прочности, учитывающие погрешность приближенных решений. Для удобства и непрерывности изложения в теореме 2 используются обозначения, введенные в теореме 1.

Теорема 2. Пусть для упругой конструкции V^b заданы условия прочности (14) и определено максимальное эквивалентное напряжение а _b , отвечающее приближенному решению задачи упругости. Пусть

1 5 1 <5 _р < C p

A n n^p + n^p ,

где An =| n2p - np |, np, n2 - заданы; 5 - относитель ная погрешность для напряжения аь, т. е.

5 = а^15а0-, (16) а b где а0 - максимальное эквивалентное напряжение конструкции Vb , отвечающее точному решению задачи упругости, напряжения аЬ, аb определяются по 4-й теории прочности, 5p - оценка для погрешности 5 .

Пусть коэффициент запаса nb конструкции, отвечающий приближенному решению, удовлетворяет скорректированным условиям прочности вида n1p

¹ — ⁵ p

< ⁿ b <

n ₂ ^p

1 + 5 p

где n_b = а T / а _b , а T - предел текучести.

Тогда коэффициент запаса n_b ⁰ конструкции, отвечающий точному решению, удовлетворяет заданным условиям прочности (14), где п 0 = а T / а ь .

Доказательство. Из (16) следует аь = (1 + 5) а0. Отсюда получаем п = (1 + 5)пь.(18)

Отметим, что в (15) C p <  1. Пусть 5 ₀ такое, что 5 ₀ = | 5 |. Тогда в силу (15) имеем соотношения

0<5о = |5| <5p < 1.(19)

Принимая в (18) последовательно 5 = -50, 5 = 50, введем коэффициенты пГ = (1 -50)пь, п2 = (1 + 50)пь,(20)

Тогда в силу (18), (20) получаем пЬ = пГ или п0 = п2.(21)

Введем коэффициенты n1d , n2d по формулам пр = (1 -5 p)пь, п2d = (1 + 5p)пь.(22)

В силу того, что 0 <5g < 1, пь > 0 , из (22) следует п2d > пр .(23)

Пусть для коэффициента nb выполняются условия прочности (17), т. е. пусть п’ < (1 -5p)пь, (1 + 5p)пь < п’ .

Тогда для коэффициентов n1d , n2d с учетом (23) выполняются неравенства п’ < пр < пd < п!p.              (24)

Сравнивая (20), (22) с учетом (19), следуют неравенства drrd п1 < п1 , п 2 < п 2 .

Отсюда, учитывая, что согласно (19) пГ < п2, по лучаем drrd п1 < п1 < п2 < п2 .               (25)

Тогда в силу (24), (25) выполняются неравенства п1p < п[ < п2 < п’ .

Из выполнения (26) с учетом (21) следует выполнение заданных условий прочности (14) для коэффициента запаса п0 . Ограничения на параметр 5p нахо- дим из предположения существования условий прочности (17), т. е. пусть пp < _n2L

1 — 5 p 1 + 5 p

.

Откуда следует pp

А п

.

п 1 p + п Р

Отметим, что поскольку п ₂ >  п ’ >  1, то из (28) следует 0 <  C_p <  1. Если 5 _p = C_p , то диапазон для варьирования значений коэффициента n_b равен нулю, т. е. в этом случае п_ь = ( п р ¹ + п 2 )/ 2, что трудно выполнить на практике при заданных n ₁ ^p , n ₂ ^p . Итак, при 5 _p <  C p возможно выполнение заданных условий прочности (14) для коэффициента n_b ⁰ с применением скорректированных условий прочности (17) и приближенного решения, которое порождает для напряжения а _ь такую погрешность 5 , что 1 5 1 <5 _p . Теорема 2 доказана .

Скорректированные эквивалентные условия прочности, учитывающие погрешность напряжений. На практике для решения задач теории упругости, сформулированных для трехмерных композитных конструкций, применяются численные методы, например ММКЭ [10–12], которые порождают решения с малой погрешностью. В связи с этим возникает необходимость учитывать погрешность решений в эквивалентных условиях прочности. В работе [16] рассматриваются эквивалентные условия прочности без учета погрешности приближенных решений. Используя результаты работы [4], на основе теорем 1, 2 сформулируем скорректированные эквивалентные условия прочности, которые учитывают погрешность решений. Скорректированные эквивалентные условия прочности отражает следующая теорема, в которой используются обозначения, введенные в теоремах 1, 2.

Теорема 3. Пусть для коэффициента запаса упругой изотропной однородной конструкции Vb определены эквивалентные условия прочности вида п? < п0 < п^ ,                 (29)

где n ₁ ^p , n ₂ ^p – заданы, т. е. определен параметр p (см. теорему 1); n_b ⁰ – коэффициент запаса прочности конструкции V^b , отвечающий точному решению трехмерной задачи упругости, сформулированной для конструкции V^b . Пусть для конструкции V^b определено максимальное эквивалентное напряжение а ь , отвечающее приближенному решению задачи упругости. Пусть

Ли

1 5 1 <5„< C„ =--------,            (30)

p p пр + п!’ где Ап =| п2 - п’ |, 5 - относительная погрешность для напряжения а ь, т. е. 5 = (а ь -а 00)/ а 0, где аь -максимальное эквивалентное напряжение конструкции Vb , отвечающее точному решению задачи упругости, 5p - оценка для погрешности 5 .

Пусть коэффициент запаса nb конструкции, отвечающий приближенному решению, удовлетворяет скорректированным эквивалентным условиям прочности вида

n ₁ ^p

¹ -⁵ p

< nb <

n ₂ ^p

1 + 5 p

Если толщина волокон меньше 0,5 мм, то такие волокна образуют микронеоднородную структуру [17]. Пусть L = 600 мм, H = 50 мм , тогда h = 0,3906 мм, т. е. балка V ₀ размерами 5 х 60 х 5 см имеет микроне-однородную регулярную волокнистую структуру.

где n b = g T / g _b , g T - предел текучести.

Тогда коэффициент запаса nb0 конструкции, отвечающий точному решению, удовлетворяет эквива лентным условиям прочности (29), где nb = gT / g^ .

Доказательство теоремы 3 аналогично доказательству теоремы 2. Отметим, что 5p можно рассматривать как максимальную погрешность для максимального эквивалентного напряжения gь конструкции Vb . Соотношения (31) представим в виде np (1 + 61) < Пь < np (1 — S2), или, учитывая (13), имеем

Pn 1^{(1 + S} 1 ) <  n b <  pn 2 ⁽¹ — S 2 ),

где величины 81, 82 определяются с помощью по грешности 5p напряжения gь по формулам

Si= —--1, s₂ = 1-- —, 0 <5 <  1, (33)

1 1 -5p 2      1 + 5p        p здесь p – коэффициент эквивалентности.

Основные положения метода эквивалентных условий прочности. Рассмотрим консольную композитную балку V ₀ регулярной структуры (которая расположена в декартовой системе координат Oxyz ) длиной L = 1536 h = 600, квадратного сечения размерами H х H , где H = 128 h = 50 (рис. 1). Балка V 0 состоит из пластичных материалов и имеет статическое нагружение q_z ( x , y , z ).

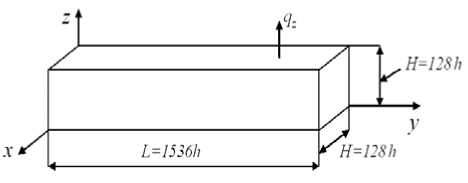
Рис. 1. Характерные размеры балки V ₀

Fig. 1. The characteristic sizes of the beam V ₀

Регулярная ячейка G ₀ композитной балки V ₀ имеет размеры 8 h х 8 h х 8 h , в которой расположены продольные волокна сечением h х h (рис. 2, сечения волокон закрашены, 16 волокон). Таким образом, балка армирована продольными волокнами – сечением h х h , расстояние между волокнами равно h . Волокна являются изотропными однородными телами и имеют одинаковые модули упругости.

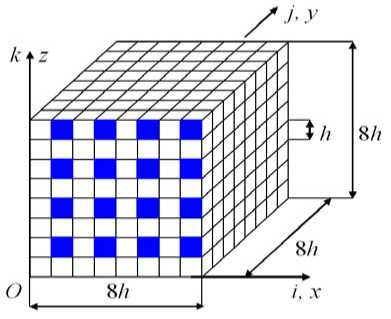
Рис. 2. Регулярная ячейка G ₀

Fig. 2. Regular cell G ₀

Для коэффициента запаса n ₀ композитной балки V ₀ заданы условия прочности вида (5). Требуется определить коэффициент запаса n ₀ данной балки, т. е. проверить, удовлетворяет ли балка V ₀ заданным условиям прочности. Для решения данной задачи используем МЭУП, основные положения которого рассмотрим (для простоты изложения, не теряя общности суждений) на примере балки V ₀ с микронеод-нородной регулярной структурой. Базовое регулярное разбиение R ₀ балки V ₀ состоит из (базовых) односеточных КЭ (1сКЭ) V_j^h 1-го порядка формы куба со стороной h [8], в которых реализуется трехмерное НДС. Разбиение R ₀ учитывает микронеоднородную структуру балки, порождает равномерную мелкую (базовую) сетку с шагом h размерности 129 х 1537 х 129 и дискретную модель с общим числом узловых неизвестных МКЭ N ₀ = 76681728, ширина ленты системы уравнений (СУ) МКЭ равна b ₀ = 50316 . Реализация МКЭ для базовой модели R ₀ (более 76 млн узловых неизвестных) требует больших ресурсов ЭВМ. Построение последовательности решений связано с применением процедуры измельчения базового разбиения, которая для композитной структуры балки V ₀ является сложной и труднореализуемой, так как каждый шаг измельчения приводит к резкому увеличению размерности дискретной задачи. Отметим, что шаг базового регулярного разбиения R ₀ композитной балки V ₀ не может быть больше h , так как сечение волокна имеет размеры h х h .

Согласно МЭУП, введем изотропную однородную балку Vb такую, что балки Vb , V0 имеют одинаковые форму, размеры, заданные закрепления и нагружения, но отличаются модулями упругости. Модули упругости балки Vb равны модулям упругости волокна балки V0. Реализация МЭУП сводится к построению скорректированных эквивалентных условий прочности (32) и к определению коэффициента запаса nb тела Vb, т. е. к определению коэффициента эквивалентности p для балки V0 и к определению с помощью МКЭ максимального эквивалентного напряжения gb для тела Vb с погрешностью 5p . Коэффициент p определяется по формуле p = g0 / gb, где g0 , gb - максимальные эквивалентные напряжения соответственно тел V0, Vb. Отметим, что нахождение напряжения g0 по МКЭ (с применением односеточных КЭ формы куба со стороной h [8]) для балки V0 с учетом ее микронеоднородной структуры требует больших ресурсов ЭВМ.

Для нахождения коэффициента эквивалентности p и напряжения g b предлагается следующая процедура. Для изотропного однородного тела V b строим последовательность базовых регулярных разбиений (дискретных моделей) { V n } N L1 , состоящих из базовых 1сКЭ V j ⁿ ) 1-го порядка формы куба со стороной h_n . Дискретная модель V_n ⁰ имеет размерность n ^{( n} ) х n 2 ⁿ ) x n 3 ⁿ ) , где

n(n) = 8n +1, n2n) = 96n +1, n3n) = 8n +1, n = 1,...,N. (34)

Шаги базовой сетки по осям Ox , Oy , Oz равны h X ⁿ ) = H /(8 n ), h y ⁿ ) = L /(96 n ), h z ⁿ ) = H /(8 n ), так как L = 12 H , то h_n = h x ⁿ ) = h yn ) = h z ⁿ ) , причем, h_n >  h , n = 1,..., N - 1. Отметим, что при n = N получаем h_N = h (для закона измельчения (34) при N = 16 имеем h ₁₆ = h ), т. е. при n = 16 размерности изотропной однородной дискретной модели V ₁⁰₆ и базового разбиения R ₀ композитной балки V , одинаковы. Важно отметить следующее. Закон измельчения для разбиений задается так, что каждое разбиение V_n ⁰ состоит из конечного числа одинаковых по форме и размерам таких областей G n , что область G n и область регулярной ячейки G ₀ (рис. 2) имеют одинаковую форму, но отличаются характерными размерами. Для заданного закона измельчения (34) область G_n^b имеет размеры 8 h_n х 8 h_n х 8 h_n . Область G b отличается от области регулярной ячейки G ₀ (размерами 8 h х 8 h х 8 h , см. рис. 2) характерными размерами вида h_n = в _nh , где в _n >  1. При n ^ 16 имеем в _n ^ 1, при n = 16 получаем в ₁₆ = 1.

Введем область G_n ⁰ , форма и характерные размеры которой совпадают с областью G b , n = 1,..., N . При этом область G_n ⁰ имеет композитную структуру, которая по виду совпадает со структурой регулярной ячейки G ₀ , т. е. область G_n ⁰ имеет такое же число волокон (с квадратным сечением размерами h_n х h_n ) и такое же их взаимное расположение, как в ячейке G ₀ (16 продольных волокон, см. рис. 2). Волокна в областях G_n ⁰ , G ₀ имеют одинаковые модули упругости. Области G_n ⁰ , G ₀ , по сути, отличаются только масштабностью, т. е. формально можно записать G n = в _nG₀ , где в _n — коэффициент масштабности, в _n >  1, n = 1,..., N - 1. При n = N получаем в N = 1, т. е. G N = G ₀. Для закона измельчения (34) при n = 16 имеем в ₁₆ = 1, т. е. G ⁰, = G ₀. Отметим, что в области G n учитывается неоднородная (волокнистая) структура.

Заменяем в дискретной модели V_n ⁰ все однородные изотропные области G_n^b на композитные области G_n ⁰ . В результате на основе изотропной однородной модели V_n ⁰ получаем композитную (базовую) дискретную модель, которую обозначим через R n (в которой учитывается неоднородная структура). Таким образом, при n = 16 композитная дискретная модель R ₁⁰₆ совпадает с базовой моделью R ₀ композитной балки V ₀, т. е. имеем R '6 = R ₀. Итак, дискретные модели V_n ⁰ , R_n ⁰ имеют одинаковую форму, характерные размеры и размерность, одинаковые закрепления и нагружения, но отличаются модулями упругости. Согласно (34) размерности моделей V_n ⁰, R n резко возрастают при увеличении n . Для понижения размерности дискретных моделей эффективно применяются МнКЭ [10; 11; 13; 14]. Используя m - сеточные КЭ в дискретных базовых моделях V_n ⁰, R 0 , получаем соответственно m - сеточные дискретные модели V_n^b , R_n , которые имеют одинаковую форму, характерные размеры, размерность, одинаковые закрепления и нагружения как балка V ₀ , но отличаются модулями упругости. Размерности m - сеточных дискретных моделей V_n^b , R_n значительно меньше размерностей соответственно базовых моделей V_n ⁰ , R_n ⁰ . Процедура определения коэффициента эквивалентности p заключается в следующем. Для дискретных моделей V_n^b , R_n определяем соответственно максимальные эквивалентные напряжения g n , g _n , с помощью которых находим коэффициент p_n =g _n / g n , n = 1,..., N . Имеем p_n ^ p при n ^ N . Пусть

8 n = 1 P n - P n -1 I / P_n есть малая величина, тогда принимаем p = p n . Пусть построена последовательность решений { а n ^, которая быстро сходится к точному решению и пусть 5 ^ = | а n - а n -1 | / а n малая величина. Тогда считаем, что а n есть максимальное эквивалентное напряжение изотропного однородного тела V b (найденное с погрешностью 5 _p ). Подставляя полученные p , 5 _p и заданные коэффициенты n 1 , n 2 в (32), определяем скорректированные эквивалентные условия прочности для композитной балки V ₀ . Коэффициент запаса n_b для тела V^b находим по формуле n b = а T / а П , где а T - предел текучести волокна. Если найденный коэффициент n_b удовлетворяет полученным скорректированным эквивалентным условиям прочности вида (32), то коэффициент запаса n ₀ композитной балки V ₀ (см. рис. 1) удовлетворяет заданным условиям прочности вида (5).

Результаты численных экспериментов. Рассмотрим модельную задачу о расчете на прочность консольной балки V ₀ с микронеоднородной волокнистой регулярной структурой размерами 128 h х 1536 h х 128 h , h - мало, задано (см. рис. 1). Балка V ₀ состоит из пластичных материалов, имеет квадратное сечение размерами H х H , где H = 128 h . Регулярная ячейка микронеоднородной структуры балки V 0 размерами 8 h х 8 h х 8 h имеет 16 одинаковых продольных волокон сечением h х h (см. рис. 2), т. е. балка армирована изотропными однородными продольными волокнами сечением h х h , расстояние между волокнами равно h . При у = 0 : u = v = w = 0, т. е. в плоскости xOz , балка V ₀ закреплена. Для коэффициента запаса n ₀ балки V ₀ заданы условия прочности вида

1,3 <  n ₀ <  3,2. (35)

Для балки V ₀ используем следующие исходные данные:

h = 0,3906 ; аT = 5 ; Ev = 10, Ec = 1, vc = vv = 0,3, qz = 0,0018, (36)

где E c , E_v ( v _c , v _v ) - модули Юнга (коэффициенты Пуассона) соответственно связующего материала и волокон, а T - предел текучести волокна, нагрузка q z действует на поверхности z = H , 0,5 L <  у <  L (см. рис. 1).

Для расчета балки V0 используем МЭУП с применением МнКЭ. В расчетах используем однородные и композитные лагранжевые трехсеточные КЭ (3сКЭ) формы прямоугольного параллелепипеда. Основные положения построения 3сКЭ рассмотрим на примере композитного 3сКЭ V® формы прямоугольного параллелепипеда размерами 8h х16h х 8h [10; 15]. 3сКЭ Va(3) расположен в локальной декартовой системе координат Oxyz , который содержит две регулярных ячейки G0 размерами 8h х 8h х 8h композитной балки V0 . Вначале рассмотрим процедуру построения композитного лагранжевого двухсеточного КЭ (2сКЭ) Vd(2) размерами 8h х 8h х 8h, который содержит одну регулярную ячейку G0 . В процедуре используем равномерную мелкую сетку hd с шагом h размерности 9 х 9 х 9 и крупную сетку Hd, вложенную в мелкую, Hd с hd . На рис. 3 показана мелкая сетка hd и крупная сетка Hd , имеющая 125 узлов, которые отмечены точками. Мелкая сетка hd порождена базовым разбиением Rd 2сКЭ Vd(2) , которое состоит из 1сКЭ Vjh 1-го порядка формы куба со стороной h (в которых реализуется трехмерное НДС, j = 1,...,M , M - общее число 1сКЭ Vj, M = 512) и которое учитывает микронеоднородную структуру 2сКЭ Vd(2) . Волокна параллельны оси Oy , сечения волокон в плоскости Oxz закрашены, 16 волокон (рис. 3).

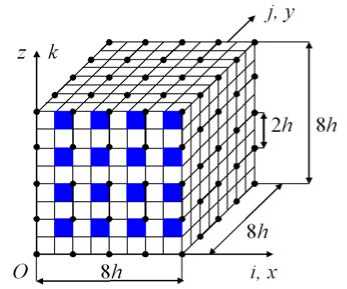
Рис. 3. Мелкая и крупная сетки 2сКЭ V_d ⁽²⁾

Fig. 3. Small and large mesh 2gFE V_d ⁽²⁾

Полную потенциальную энергию П _d базового разбиения R_d 2сКЭ V_d ⁽²⁾ представим [5; 8]

П d = Z (т q T [ K h ] q j - q^ y ),        (37)

j =1 ²

где [ K^h_j ] – матрица жесткости, P _j , q _j – векторы узловых сил и перемещений 1сКЭ V_j^h базового разбиения 2сКЭ, T – транспонирование.

С помощью полиномов Лагранжа [5] на крупной сетке H_d определяем аппроксимирующие функции перемещений u ₂, v ₂, w ₂ для 2сКЭ V_d ⁽²⁾, которые запишем в форме

555       555

u 2 = ∑∑∑ N ijk u ijk , v 2 = ∑∑∑ N ijk v ijk , i =1 j =1 k =1                          i =1 j =1 k =1

w 2 = ∑∑∑ N ijk w ijk ,         (38)

i =1 j =1 k =1

где u_ijk , v_ijk , w_ijk – значения перемещений u , v , w в узле i , j , k сетки H_d ; i , j , k – координаты целочисленной системы координат ijk , введенной для узлов сетки H_d (см. рис. 3); N_ijk = N_ijk ( x , y , z ) – базисная функция узла i , j , k сетки H_d , i , j , k = 1,...,5, N_ijk = L_i ( x ) L_j ( y ) L_k ( z ), где

L i ( x ) = ∏ ^{5 x - x α} , L j ( y ) = ∏ ^{5    y - y α} ,

α=1,α≠ i x i ^- x α            α=1,α≠ j y j ^- y α

L k ( z ) = ∏ ^{zz α} ,          (39)

α=1,α ≠ k zk - zα здесь xi,yj,zk – координаты узла i,j,k сетки Hd в системе координат Oxyz (см. рис. 3).

Обозначим: Nβ =Nijk, uβ =uijk,     vβ =vijk, wβ = wijk, где i, j,k= 1,...,5, β =1,...,125 . Тогда выражения (38) принимают вид

125                125125

u2 = ∑Nβuβ, v2 = ∑Nβvβ, w2 = ∑Nβwβ.(40)

β=1               β=1

Обозначим через qd ={u1,...,u125, v1,...,v125, w1,...,w125}T вектор узловых перемещений сетки Hd , т. е. вектор узловых неизвестных 2сКЭ Vd(2) . Используя (40), компоненты вектора q j узловых неизвестных 1сКЭ Vjh выражаем через компоненты вектора qd , в результате получим равенство qj =[A2j] qd,(41)

где [ A ² _j ] – прямоугольная матрица, j = 1,..., 512 .

Подставляя (41) в выражение (37), из условия ∂ П_d / ∂ q _d = 0 получаем [ K_d ] q _d = F _d , где

[Kd]=∑[A2j]T[Khj][A2j], Fd=∑[A2j]TPj,(42)

j=1

здесь [ K_d ] – матрица жесткости (размерности 375 × 375 ), F _d – вектор узловых сил (размерности 375) 2сКЭ V_d ⁽²⁾.

Рассмотрим построение лагранжевого трехсеточного КЭ (3сКЭ) V _α ⁽³⁾ , используя два 2сКЭ V_d ⁽²⁾ . Мелкая h _α и крупная H _α сетки 3сКЭ V _α ⁽³⁾ показаны на рис. 4, узлы сетки H _α отмечены точками, 12 узлов. Узлы мелкой сетки h _α являются узлами крупных сеток H_d двух 2сКЭ V_d ⁽²⁾ , d = 1, 2 .

Полную потенциальную энергию П _α 3сКЭ V _α ⁽³⁾ представим в форме

П α = ∑ (¹ q ^T d [ K d ] q d - q ^T d F d ),         (43)

d =1 2

где [ K_d ], F _d , q _d – матрица жесткости, векторы узловых сил и перемещений 2сКЭ V_d ⁽²⁾ , d = 1, 2 .

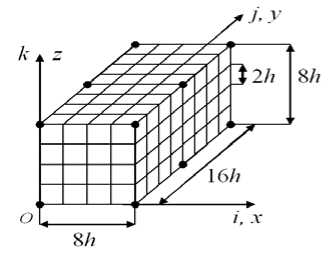
Рис. 4. Мелкая h _α и крупная H _α сетки 3сКЭ V _α ⁽³⁾

Fig. 4. Small h _α and large H _α mesh 3gFE V _α ⁽³⁾

С помощью полиномов Лагранжа на крупной сетке H _α определяем аппроксимирующие функции перемещений u ₃, v ₃, w ₃ для 3сКЭ V _α ⁽³⁾ , которые запишем в форме

232       232

u 3 = ∑∑∑ N ijk u ijk , v 3 = ∑∑∑ N ijk v ijk , i =1 j =1 k =1                          i =1 j =1 k =1

w 3 = ∑∑∑ N ijk w ijk ,          (44)

i =1 j =1 k =1

где u_ijk , v_ijk , w_ijk – значения перемещений u, v, w в узле i , j , k сетки H _α ; i , j , k – координаты целочисленной системы координат ijk , введенной для узлов сетки H _α (см. рис. 4); N_ijk = N_ijk ( x , y , z ) – базисная функция узла i , j , k сетки H _α , i , k = 1,2, j = 1,2,3 , N_ijk = L_i ( x ) L_j ( y ) L_k ( z ), где

L i ( x ) = ∏ ^{x - x α} , L j ( y ) = ∏ ^{y - y α} , α=1,α≠ i x i ^- x α            α=1,α≠ j y j ^- y α

L k ( z ) = ∏ ^{zz α} ,          (45)

α=1,α ≠ k zk - zα здесь xi,yj,zk – координаты узла i,j,k сетки Hα в системе координат Oxyz , рис. 4.

Обозначим: N _β = N_ijk , u _β = u_ijk , v _β = v_ijk , w _β = w_ijk , где i , k = 1, 2, j = 1, 2, 3 , β = 1,...,12 . Тогда выражения (44) принимают вид

12                  1212

u3= ∑Nβuβ, v3= ∑Nβvβ, w3=∑Nβwβ.(46)

β=1                 β=1

Обозначим через qa = {u1,...,u12, v1,...,v12, w,,...,w12}T вектор узловых перемещений крупной сетки Ha , т. е. вектор узловых неизвестных 3сКЭ Va3). Используя (46), компоненты вектора qd узловых неизвестных 2сКЭ Vd(2) выражаем через компоненты вектора qa, в результате получим qd = [Ad] qa, (47)

где [ A d ] - прямоугольная матрица, d = 1, 2 .

Подставляя (47) в выражение (43), из условия ^д П a / ^a = ⁰ получаем ^[ K a ^] q„ = F a , гДе

2 2

[ K a ] = Е [ A d ] T [ K d ][ A d ], F ^ ' A d ] T F d , (48) d =1 d =1

здесь [ K _a ] - матрица жесткости (размерности 36 x 36), F _a - вектор узловых сил (размерности 36) зскэ v a ³⁾.

Замечание 2. Решение, построенное для крупной сетки H _a 3сКЭ V j ³⁾, с помощью формулы (47) проецируется на мелкую сетку h _a 3сКЭ V ⁽³⁾. Затем, с помощью формулы (41) определяем узловые перемещения базовых разбиений 2сКЭ V / ²’, что дает возможность вычислять напряжения в любом 1сКЭ V j базового разбиения R d 2сКЭ V_d^{( 2)}, d = 1, 2 .

Замечание 3. В силу (41) размерность вектора q _d (т. е. размерность 2СКЭ V_d ⁽²⁾) не зависит от общего числа M 1сКЭ V j , т. е. от размерности разбиения R d . Поэтому для учета в 2сКЭ микронеоднородной структуры можно использовать сколь угодно мелкие базовые разбиения R d , состоящие из 1сКЭ V j . В этом случае в 2сКЭ V_d^{( 2)} (следовательно, и в 3сКЭ V a ³⁾) сколь угодно точно описывается трехмерное НДС (без введения дополнительных упрощающих гипотез).

С помощью процедур, изложенных в работе [14], проектируются 2сКЭ для расчета композитных оболочек вращения, колец сложной формы и валов, которые имеют центральные круговые отверстия, композитных и однородных цилиндрических оболочек, пластин и балок сложной формы, которые широко используются на практике. Процедура построения однородных МнКЭ аналогична процедуре построения композитных МнКЭ.

Для композитной балки V0 определяем изотропное однородное тело V4 (балку V4). Тела V0, V4 имеют одинаковые форму, размеры, закрепление и нагружение, модули упругости тела Vb равны модулям упругости волокна. Используя закон измельчения (34), строим по процедуре, описанной выше, трехсеточные дискретные модели Vb, Rn, состоящие соответственно из изотропных однородных и композитных 3сКЭ типа V*3) размерами 8hn x16hn x 8hn, n = 1, 12. Для дискретной изотропной однородной модели Vb находим решения wb, с4n, где wb, с4 -максимальные перемещение и эквивалентное напряжение дискретной модели Vb, n = 1,...,12 . Эквивалентные напряжения определяем по 4-й теории прочности. Результаты расчетов представлены в табл. 1. Анализ результатов расчетов показывает быструю равномерно монотонную сходимость приближенных решений (wb, сn) к точному. Напряжения cb1 = 0,665 , ab2 = 0,686, отличаются на 5 = 3,061 % . Тестовые расчеты показывают, что в этом случае напряжение ab2 найдено с погрешностью 10 +15%. Принимаем 5p = 0,15. Условие (30) для 5p выполняется. Учитывая в (30) соотношения (13), (35), имеем 5p = 0,15 < Cp = 0,42. Согласно (33) при 5p = 0,15 получаем s1 = 0,176, s2 = 0,131. Скорректированные эквивалентные условия прочности (32) для s1 = 0,176 , s2 = 0,131 имеют вид

1,176 pn₁ < n₄ < 0,869 pn ₂,            (49)

где n b - коэффициент запаса тела V⁴ , определяемый с помощью МКЭ.

Результаты расчетов балки V ^b

V n b	b w n	a 4	V n b	b wn	σ bn
V	204,851	0,377	V 7 b	238,033	0,569
V	228,503	0,489	V	238,263	0,595
V	234,023	0,524	V 9 4	238,422	0,620
	236,109	0,537	V	238,545	0,643
V	237,119	0,543	v 4	238,630	0,665
V	237,683	0,547	V	238,697	0,686

Отметим, что трехсеточная дискретная модель V j, состоящая из лагранжевых 3сКЭ типа V a ³⁾

( a = 1,...,32768) размерами 8 h ₁₂ x 16 h ₁₂ x 8 h ₁₂, имеет

N b ₂ = 73008 узловых неизвестных МКЭ, ширина ленты СУ МКЭ равна 4₁₂ = 1059. Реализация МКЭ для дискретной модели V ₁ ^b ₂ требует

в

к =        = ^{76681728 x 50316} = 49903,566

N b ₂ x b ₁₂     73008 x 1059

раз

меньше объема памяти ЭВМ, чем для базовой модели R0 балки V0, что показывает высокую эффектив ность применения лагранжевых 3сКЭ типа V(3 в расчетах. Коэффициент эквивалентности p для компо- зитной балки V0 определяем с помощью процедуры, которая описана выше. Дискретные модели Vnb , Rn , n = 9, 11, 12 построены с помощью 3сКЭ типа р3) на основе базовых регулярных разбиений соответственно размерностей: 73 х 865 х 73, 89 х1057 х 89 и 97 х1153 х 97. Коэффициенты эквивалентности pn находим по формуле pn = an / an, где an, an - максимальные эквивалентные напряжения соответственно моделей Rn, Vnb, n = 9, 11, 12 . В результате расчетов получаем: p9 = 3,002, p11 = 3,000, p12 = 2,999. Относительные погрешности для найденных коэффициентов p9 , p11 , p12 равны

5 1 (%) = 100% х | p _п - p 9 |/ р и = = 100% х 13,002 - 3,0001 /3,000 = 0,066%’

5 ₂(%) = 100% х | p 22 - p _n|/ _А2 = = 100% х 13,000 - 2,9991 /2,999 = 0,033% ^.

Поскольку p ₉ >  p 11 >  p ₁₂ и 5 2 самая малая величина, то считаем, что коэффициент эквивалентности равен p = p ₁₂ = 2,999. Подставляя в (49) p = 2,999, n 1 = 1,3, n ₂ = 3,2, получаем

4,584 <  n b <  8,339. (50)

Коэффициент запаса однородного тела V^b равен n_b = a T / a b ₂ = 5 / 0,686 = 7,288, который удовлетворяет скорректированным эквивалентным условиям прочности (50). Это означает, что коэффициент запаса n ₀ композитной балки V ₀ удовлетворяет заданным условиям прочности (35).

Проведем проверочные расчеты. На основе базового разбиения R ₀ балки V ₀ с применением 3сКЭ Р ^ ³ ) строим трехсеточные дискретные модели: композитную R ₁₆ и изотропную однородную R ₁ ^b ₆ , отвечающие закону измельчения (34) при n = 16. Считаем, что напряжения a ₁₆ = 2,279, a b ₆ = 0,762 отвечают точным решениям, т. е. a ₀ = a ₁₆ , a _b = a b ₆. Тогда коэффициент запаса для композитного тела V ₀ равен n ₀ =a T / a ₀ = 5/2,279 = 2,194, т. е. n ₀ = 2,194 удовлетворяет заданным условиям прочности (35), что подтверждает аналогичный вывод, полученный с помощью МЭУП.

Коэффициент эквивалентности p ₀ (отвечающий точным решениям) для балки V ₀ равен p ₀ =a ₀/ a _b = 2,279/0,762 = 2,990. Отметим, что коэффициенты p = 2,999 и p ₀ = 2,990 отличаются на 0,301 %, т. е. в самом деле, можно принять p ₀ = p .

Размерность базовой дискретной модели V102 (сетка которой при n = 12 имеет размерность 97 х 1153 х 97 , см. формулы (34)) равна 32517504, ширина ленты СУ МКЭ равна 28524. Число узловых неизвестных МКЭ трехсеточной дискретной модели V1b2 равно 73008, ширина ленты СУ МКЭ равна 1059. Реа- лизация МКЭ для однородной изотропной трехсеточ- ной дискретной модели   V1b2    требует в k 2 =

32517504 х 28524 73008 х 1059

= 11996,685 раз меньше объема памяти ЭВМ, чем для базовой модели V102 , состоящей из известных 1сКЭ формы куба со стороной h12 .

Заключение. Предложен метод эквивалентных условий прочности для расчета на статическую прочность конструкций (пластины, балки, оболочки) с неоднородной, микронеоднородной регулярной структурой при заданных условиях прочности. Реализация метода сводится к расчету на прочность изотропных однородных тел с применением эквивалентных условий прочности, построенных на основе заданных. При расчете однородных тел по МКЭ используются МнКЭ, которые порождают дискретные модели малой размерности и решения с малой погрешностью. Реализация предлагаемого метода требует малых ресурсов ЭВМ.