Метод эмпирических категориальных коррелограмм и его применение

В самом общем случае любая случайная функция натурального аргумента t (или временной ряд) может быть представлена в следующем виде [1]:

X ( t ) = A ( t ) sin(m( t ) t + v( t )).

В связи с этим, самая большая сложность, встречаемая в спектральном анализе, заключена в оценке параметров A ( t ) – амплитуды колебаний, ω( t ) – их частоты и ψ( t ) – фазового сдвига колебаний, которые являются также функциями времени. Проиллюстрируем эту проблему на примере оценки частоты колебаний.

Проанализируем взаимосвязи спектров циклических компонент, которые обладают примерно одинаковыми частотами. Отметим, что при определенных условиях циклические компоненты с близкими частотами будут линейно-независимыми, в частности, линейные корреляции между ними будут равны 0 [2]. Это вытекает из свойства, которое широко используется при преобразованиях Фурье, Хартли и различных модификаций этих методов [2]. А именно набор гармоник {sin(2n ■ t -1/ j), где j = 2п/k, k - целое} образует базис в бесконечно-мерном функциональном пространстве. На практике, в силу жестких ограничений (например, стационарность исходных временных рядов), накладываемых на использование чистого преобразования Фурье [2], широкое распространение получили методы (SSA, MTM или CWT), для которых такие ограничения не столь критичны.

Существует ряд классических примеров, которые показывают сложность определения при спектральном анализе истинных частот для временных рядов, встречаемых в различных областях естественных наук. Эти ряды, как правило, отличаются наличием нестационарных амплитуды, фазовых сдвигов и «колорированного» шума, кото- рый может полностью изменить спектр изучаемого природного процесса.

Автором предлагается новый алгоритм спектрального анализа - метод эмпирических категориальных коррелограмм (МЭКК), который позволяет с высокой степенью вероятности определять истинные частоты и фазовые сдвиги как для количественных данных, так и качественных (категориальных) временных рядов. Примером последних могут служить косвенные данные о климатических изменениях, привязанные к временной шкале. Отметим, что такие наблюдения за климатическими событиями отличаются нерегулярностью при их фиксации во времени, а именно большим количеством пропусков самих событий во времени [3; 4]. Последнее объясняется несовершенством методики фиксации, сбора и обработки подобных сведений в доинструментальной исторической эпохе обработки климатической информации [4].

Описание алгоритма МЭКК. Преобразуем анализируемый временной ряд (ВР) по следующему правилу Во-первых, проведем группировку с равными интервалами всех значений этого ВР [5]. При этом, количество групп М определим при помощи известной формулы Стерджесса, т е. М = Целое (1 + Ln( N )), а длину группиро-вочного интервала h - как h = ( 5 _max - 5 _тш)/ M , где 5 _max -максимальное значение временного ряда 5 ( t ) и 5 _min -минимальное значение временного ряда 5 ( t ), соответственно. Группировочный интервал для i -группы ( i = 1... M ) определим по следующему соотношению:

д = 1 5min + (i - 1)h ; 5min + ih), если i < M, i 1 [5min + (i-1)h ; 5max], если i = M.

Далее значению категориального временного ряда 5 ( t ) в момент времени t припишем номер той группы, в группировочный интервал которой попало значение исходного временного ряда 5 ( t ).

Процедура группировки значений ВР позволяет стабилизировать амплитуду ВР и снизить влияние фонового шума на абсолютные значения исходного ВР.

Охарактеризуем каждую из М -групп средним груп-пировочным значением S k (оценкой математического ожидания для каждой к -группы, к = 1... M ), группировоч-ным среднеквадратическим отклонением о k (оценкой дисперсии для каждой к -группы) и количеством попавших в эту группу значений анализируемого ВР. Эти характеристики будут использованы при восстановлении ВР после спектрального разложения. Конечно, количество признаков для каждой образованной группы можно увеличить, например, центральными моментами более высоких порядков.

На следующем этапе будем сравнивать полученный категориальный ряд с синус-функциями {sin(2n ■ t -1/ j + ф ), ф е [0, 2п] ( j' = 2... N )}. Предварительно, каждую j - синус-функцию B j ( t ,ф) = sin(2n ■ t -1/ j + ф), ф е [0, 2п] ( j' = 2... N ), которая также представляет собой ВР, преобразуем в категориальный ВР B j ( t ) по правилу, описанному выше.

Оценим степень сходства между двумя категориальными рядами 5 ( t ) и B j ( t ) при помощи коэффициента корреляции Спирмена, который позволяет сравнивать категориальные данные. Повторим процедуру сравнения

5 ( t ) и B j ( t ) при фиксированной частоте 1/j для B j ( t , ф), последовательно изменяя фазу ф от 0 до 2 п с достаточно малым шагом 5 .

Таким образом, можно найти оптимальную фазу для каждой B j ( t ) при фиксированной частоте 1/ j путем нахождения максимального коэффициента корреляции Спирмена по ф .

В результате, можно получить коррелограмму, где по оси абсцисс откладываются значения частоты (или соответствующим им периодам), а по оси ординат - максимальные значения коэффициента корреляции Спирмена (рис. 1). Критерием определения базовых частот может служить порог значимости коэффициента Спирмена для соответствующего объема выборки N (в нашем случае -длины ВР) и выбранного уровня надежности p .

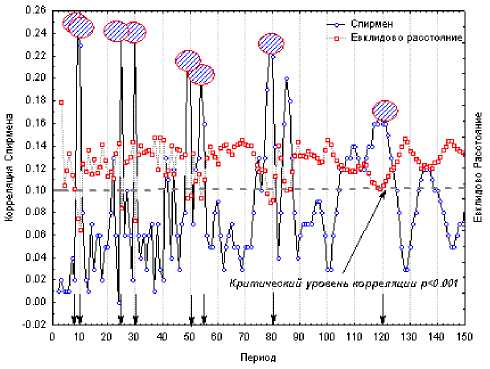
Рис. 1. Пример коррелограммы, полученной при сравнении ,$.

категориального ряда 5 ( t ) с категориальными синус-функциями B j ( t ) ( j' = 2... N )

После определения базовых частот, естественно, появляется необходимость в восстановлении чистого сигнала, т. е. исходного 5 ( t ) без аддитивной шумовой составляющей.

Для этого на основе коррелограммы определяются к ( к <  N /3), базовые частоты ю^6аз = 1 j и соответствующие им фазы ф^6аз, при которых коэффициент Спирмена достигает локальных максимумов. Далее, восстанавливается чистый сигнал 5 ( t ) на основе линейной комбинации базовых синус-функций В б аз ( t , ф), а именно

5 рек (t) = ^^AjB баз (t, ф), где все амплитуды Aj равны 1.

Отметим, когда все амплитуды A_j близки к 1, чистый сигнал 5 ^чист ( t ) (без шума) и реконструированный сигнал 5 ^рек ( t ) получаются сильно положительно коррелированными ( R = 0,89, p < 0,000 01) (рис. 2). При этом, 5 ^рек ( t ) объясняет 80 % изменчивости 5 чист ( t ). Сравним полученные результаты с корреляцией между исходным ВР 5 ( t ) и чистым сигналом 5 ^чист ( t ). В данном случае 5 ( t ) объясняет всего 30 % изменчивости 5 чист ( t ).

В случае если амплитуды Aj неизвестны, можно воспользоваться следующей процедурой: реконструированный 5рек(t), при условии Aj = 1 (j' = 1...к), перевести в категориальный ряд 5 (t) по алгоритму, описанному выше, считая, что существует взаимно-однозначное со- ответствие между группами, полученными для S(t) и Sрек(t).

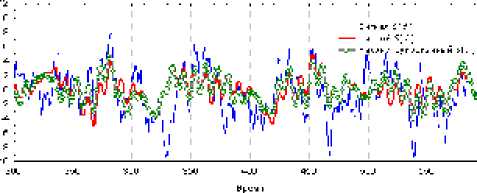
Рис. 2. Фрагмент динамики исходного сигнала S ( t ) , чистого сигнала S ^чист ( t ) (без шума) и реконструированного сигнала S ^рек ( t ) на основе метода эмпирических категориальных коррелограмм

Далее следует считать, что группировочные средние s ⁱ для каждой i -группы S ( t ) ( i = 1… M ) и соответствующие группировочные среднеквадратические отклонения σ ⁱ являются группировочными характеристиками для каждой из M -групп, полученных для S ^рек( t ).

После этого необходимо окончательно заменить номера групп S ( t ) на соответствующие группировочные средние, для которых можно указать доверительные интервалы.

Рассмотренная выше процедура спектрального анализа называется методом эмпирических категориальных коррелограмм (МЭКК).

Автром на базе вычислительного эксперимента и метода Монте-Карло проводятся исследования на статистическую устойчивость к различного рода шумовым воздействиям.

Отмечается также, что традиционные методы спектрального анализа (MTM-метод, метод максимальной эн- тропии, Вейвлет-анализ, сингулярный спектральный анализ) на подобных сильно зашумленных случайных функциях теряют до 50 % информации об истинном сигнале.

Данный метод апробирован при спектральном анализе и получении реконструкции 4-х сверхдлительных древесно-кольцевых хронологий для циркумполярной области Евразии. В реконструированных хронологиях наблюдается динамика, обратная к температурной после 1960 г.

Техническая реализация МЭКК и его исследование на статистическую устойчивость. Для проведения расчетов на основе метода эмпирических категориальных коррелограмм (МЭКК) и анализа его статистической устойчивости была разработана прикладная программа Spectral_Testing в среде программирования Delphi 5 компании Borland. Эта программа при запуске имеет стандартный вид Windows окна (рис. 3). Для использования программы необходима операционная система MS Windows XP.

При запуске программы по умолчанию будет выполняться спектральный анализ реальных временных рядов. По умолчанию указатель стоит на радиокнопке Real Data Analysis. При этом необходимо указать имя входного файла, находящегося на любом логическом диске, нажав на кнопку «Browse».

Опция «% Missing value» позволяет из исходного временного ряда выбрасывать случайным образом определенный процент значений. Эта опция позволяет исследовать полученное спектральное представление ВР на устойчивость, а именно, какой процент выброшенных значений критическим образом сказывается на спектре, изменяя его. В качестве тестового примера может выступать любой смоделированный временной ряд, для которого известны его истинные амплитуды, частоты и фазы.

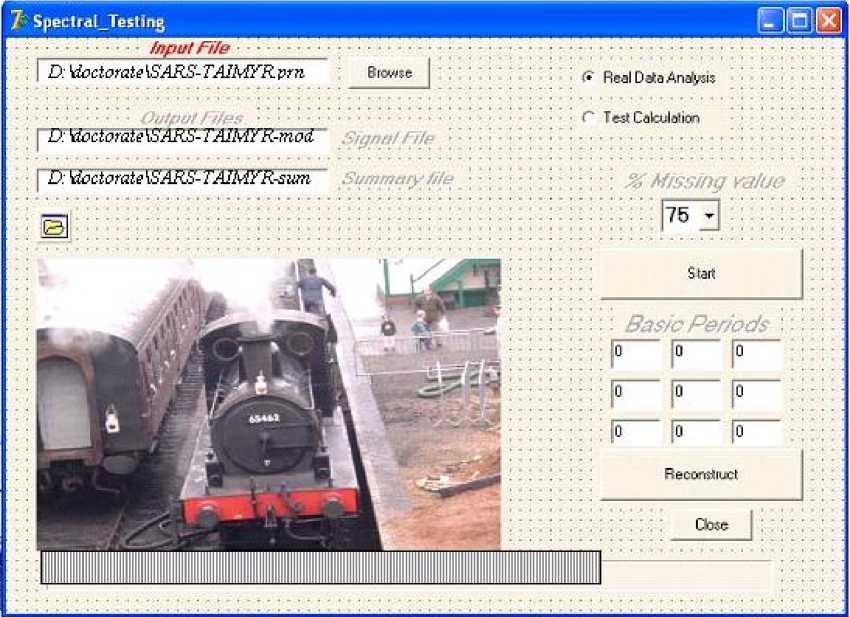
Рис. 3. Интерфейс программы Spectal_Testing, реализующей метод эмпирических категориальных коррелограмм

Для восстановления исходного ряда необходимо указать «базовые» периоды в строке «Basic periods».

Выходные данные представляются в виде двух файлов. Данные файла * summary dat представлены в 4-х столбцах в ASCII (DOS-формат): в 1-м столбце – период, 2-й столбец – соответствующая частота, 3-й столбец – максимальный коэффициент корреляции Спирмена, рассчитанный между двумя наборами категориальных данных, 4-й столбец – оптимальная фаза, при которой достигается максимальное значение коэффициента корреляции Спирмена. Также в первой строке указывается количество значений ВР, участвующих в анализе. Анализ данных этого файла позволяет принять решение о количестве базовых частот и их значениях, которые будут использованы на втором этапе анализа данных – этапе восстановления сигнала.

Рассмотрим результаты, касающиеся статистической устойчивости описанного алгоритма. В качестве исходного гармонического сигнала был использован смоделированный сигнал, на который воздействовал «красный» шум с AR(1) = 0,8 [6]. Количество реализаций такого шума было 1 000 ВР. Здесь и далее все вычислительные эксперименты имели не менее 1 000 повторностей.

Прежде всего, была исследована способность данного алгоритма выявлять базовые частоты при определенном проценте потери информации о значениях исходного временного ряда при фиксированных амплитудах, близких к 1.

Для этого последовательно выбрасывался случайным образом определенный процент значений категориального ВР. Этот процент изменялся последовательно в пределах от 5 до 80 % с шагом в 5 %. Такого рода потери информации во времени характерны при построении некоторых рядов в климатологии, дендроклиматологии, лимнологии, истории и т. д. [3; 4; 7; 8; 13].

Алгоритм стабильно выявляет все пики базовых частот в коррелограммах при выбрасывании до 75 % значений различных реализаций категориального ВР. При 80%-ных потерях информации, алгоритм МЭКК начинает терять от 2 до 4 пиков истинных базовых частот в зависимости от реализаций категориального ВР. Напомним, что таких реализаций было не менее 1 000. При анализе единичных реализаций коррелограмм только в 7 % случаев, алгоритм МЭКК ошибался при определении базовых частот, теряя 1...3 пика в высокочастотной области.

Таким образом, получено, что вероятность потерять базовую гармонику в высокочастотной области значительно выше, чем в низкочастотной, при спектральном анализе на основе МЭКК. Этот результат хорошо согласуется с теорией, разработанной для стохастических стационарных процессов [2].

Отметим также, что в теории стохастических процессов известны примеры аппроксимации эмпирических значений автокорреляционной функции простой комбинации элементарных функций. Получаемые таким образом спектральные плотности обладают рядом привлекательных свойств, а именно они являются гладкими функциями частоты, не содержащих «противоестественных пиков и провалов» [2; 9].

Но в методе МЭКК речь идет не об аппроксимации некоторой функции другими более элементарными, а о корреляционных сопоставлениях категориальных прообразов самого изучаемого процесса с прообразами простейших тригонометрических функций в те моменты времени, где определен изучаемый случайный процесс.

На практике на основе предложенного метода (МЭКК) невозможно оценить амплитудный вклад каждой из выявленной гармоники в общий сигнал. Но для восстановленного сигнала, содержащего минимальный уровень шума это можно сделать при помощи традиционных спектральных методов, таких как Вейвлет-анализа или МТМ-метода.

Применение МЭКК. Было рассмотрено 4 древеснокольцевых хронологии, полученных для Скандинавии (SCANDN), п-ова Ямал (Urals), п-ова Таймыр (Taimyr) и Северной части Якутии (Yakut). Все хронологии были получены на базе SARCS-стандартизации, являющейся робастной модификацией метода стандартизации региональными кривыми – RCS-метода [10].

При использовании МЭКК условно все выявленные периоды, которым соответствует значимый коэффициент ранговой корреляции Спирмена (р < 0,000 1), можно разбить на 4 группы: 30-летние колебания с периодом от 31 до 33 лет, 70 летние колебания с периодом от 72 до 76 лет, 90-летние колебания от 85 до 97 лет и, наконец, 150-летние колебания от 132 до 178 лет.

Отметим, что при помощи МЭКК были получены фазовые сдвиги для различных периодов (или частот). Предположим, что выявленные общие колебания являются оценкой внешнего климатического сигнала, действующего на все экосистемы для обширной территории Евразии. Тогда фазовые сдвиги могут быть интерпретированы, с одной стороны, как пространственно-временные запаздывания или опережения в действия данного сигнала на прирост древесных растений, как одного из основных индикаторов состояния экосистем. С другой стороны, такие фазовые сдвижки могут отражать региональные особенности роста древесных растений.

Динамика реконструированных сигналов древеснокольцевых хронологий на базе МЭКК отличается уже отмеченными выше опережениями и запаздываниями, несмотря на сходство выявленных значений частот. Можно также отметить, что амплитуда колебаний реконструированных хронологий меняется синхронно для всего анализируемого периода (рис. 4). Например, экстремально большие амплитуды для периодов 1450–1525, 1650–1775, 1900–2000 гг. сменяются более низкими значениями для следующих периодов: 1550–1625, 1775–1850 гг., соответственно. При этом, имеется 2 периода синхронизации (1600–1700 и 1880–1980 гг.) и 2 периода дисонхронизации в динамике реконструированных хронологий (1500–1600 и 1725–1860 гг.) (рис. 4).

Все анализируемые хронологии являются температурно-чувствительными [11; 12]. Известно также, что с 1960-х гг.

XX в. отмечается практически повсеместное увеличение летних температур в субарктической области Северного полушария [13]. Но в динамике реконструированных хронологий аналогичной тенденции не наблюдается (рис . 4). После 1960 г. в реконструированных хронологиях наблюдается динамика, обратная к температурной. Подобное расхождение в динамике прироста древесных растений и изменений летней температуры были выявлены в ряде работ. Более того, были описаны механизмы подобного расхождения в тенденциях [14; 15].

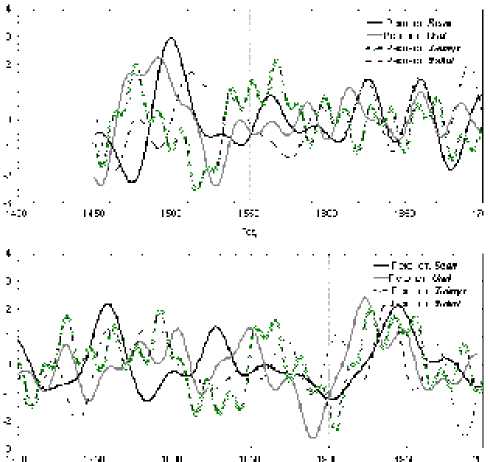
Ги,

Рис. 4. Динамика реконструирования сигналов, выявленных в супердлительных древесно-кольцевых хронологиях для двух временных периодов

На основании проведенного анализа можно сделать следующие заключения.

Предлагается новый спектральный метод к анализу категориальных данных – метод эмпирических категориальных коррелограмм (МЭКК), который является статистически устойчивым к различного рода шумовым воздействиям, даже в тех случаях, когда амплитуда колориро-ванного шума превосходит амплитуду сигнала. Разработано программное обеспечение, реализующее МЭКК.

На базе вычислительного эксперимента было показано, что алгоритм стабильно выявляет все пики базовых частот в коррелограммах при выбрасывании до 75 % значений различных реализаций категориального ВР. При 80%-ных потерях информации алгоритм МЭКК начинает терять до 70 % базовых частот, составляющих исходный сигнал.

На базе МЭКК был проведен спектральный анализ и получены реконструкции 4-х сверхдлительных древеснокольцевых хронологий для циркумполярной области Евразии. В реконструированных хронологиях наблюдается динамика, обратная к температурной после 1960 г. По- добного рода расхождение в динамике прироста древесных растений и изменений летней температуры известны в дендроклиматологии.