Метод кластеризации в системе оценки результатов работы экспертов по проверке экзаменов в форме ЕГЭ

Введение. С 2009 года в России единый государственный экзамен (ЕГЭ) является единственной формой государственной итоговой аттестации обучающихся в организациях общего среднего образования и одновременно вступительных испытаний в вузы.

По большинству предметов задания делятся на три группы в зависимости от их сложности. Первая группа — задания области А , самые простые. В них предлагается выбрать правильный ответ из предложенных вариантов. Вторая группа — задания области В. Они сложнее, предполагают самостоятельное написание краткого ответа. Ответы на задания групп А и В вносятся в бланк и проверяются с помощью компьютера. Третья группа — задания области С , самые сложные. Они требуют развернутых ответов. Например, предлагается написать эссе, привести решение задачи, дать обоснованный ответ на вопрос и т. д. Тексты ответов вносятся в бланк и проверяются экспертами региональной экспертной комиссии. Следует отметить, что нередки случаи некорректного выставления баллов экспертами при проверке заданий области С . В связи с этим конечный балл, полученный экзаменуемым, зависит не только от правильности выполненных им заданий, но и от компетентности проверяющих [1].

Таким образом, важной задачей является формирование квалифицированной экспертной комиссии, проверяющей задания области С .

В данной работе предложен метод, позволяющий ответственным за формирование предметных комиссий обосновано разделять экспертов на кластеры в зависимости от значений показателей их работы. Такая кластеризация позволит руководителям принимать решения об уровне квалификации экспертов, необходимости переподготовки некоторых из них или исключении из состава комиссии.

Ошибки при проверке экзаменационных работ. Процедура проверки экспертом экзаменационных работ области С регламентируется инструкциями Федерального института педагогических измерений (ФИПИ), которые содержат подробные схемы (алгоритмы), определяющие число баллов, выставляемых за выполнение заданий каждого варианта. Экспертам предоставляются отсканированные копии работ.

Анализ результатов работы экспертов позволяет утверждать, что при выполнении проверки возможны ошибки трех типов:

• 1)    эксперт не обнаруживает имевшееся решение задачи и, следовательно, не оценивает его;

• 2)    эксперт неверно понимает ход решения задачи;

• 3)    эксперт неверно понимает инструкцию ФИПИ по процедуре оценивания решения задания.

Ошибки 1-го типа будем называть ошибками идентификации решения [2]. Ошибки 2-го и 3-го типов будем называть ошибками оценивания.

Для сокращения влияния ошибок экспертов на оценку заданий области C предусмотрена процедура проверки решения каждого задания двумя экспертами. Процедуру проверки задания вторым экспертом будем называть второй проверкой. Если суммы баллов разных экспертов различаются несущественно, то учитывается большая из них.

Перед проведением экзамена для каждого предмета ФИПИ устанавливает критерий несущественности различия баллов. Например, при проверке заданий по математике несущественным будет отличие в два балла. Если расхождение больше, то данное задание отправляется на проверку третьему эксперту. Процедуру проверки задания третьим экспертом будем называть третьей проверкой. Третью проверку выполняет опытный эксперт высокой квалификации, выставленный им балл считается окончательным.

Основная идея метода определения корректности работы экспертов . Рассмотрим оценивание одного и того же задания разными экспертами. Примем следующие допущения.

— Оценивая задания, эксперты действуют независимо друг от друга.

— Если суммы баллов в двух случаях совпадают, то можно считать малой вероятность одновременного принятия двумя экспертами ошибочного решения.

— Если суммы баллов в двух проверках существенно различаются, то вероятность ошибки третьего эксперта мала в силу его высокой квалификации.

— Если эксперт допустил ошибку первого типа (не обнаружил задачу), то его оценка за эту задачу принимается равной 0.

— Определение корректности результатов работы экспертов основывается на значениях оценок, удельных относительно количества проверенных заданий, с учетом параметров случайных процессов.

Будем оценивать различия в баллах, выставленных за задание с номером к при второй ( А х 2 k ) и третьей ( А х 3 k ) проверке, по формулам:

А х 2 к = х 2 к - х 2 к ,                                               (1)

где х 2 k — оценка, выставленная за к -е задание i -м экспертом; х 2 k — оценка, выставленная за к -е задание j -м экспертом, в паре с которым был i -й эксперт.

Соответственно,

Ах3k = х3к - х3k,                                            (2)

где х 3 k — оценка, выставленная за к -е задание i -м экспертом; х 3 k — оценка, выставленная за к -е задание j -м экспертом, осуществляющим третью проверку.

Корректность работы экспертов в комиссии может быть оценена рядом показателей. Разделим их на четыре группы.

• 1.    Базовые выявляются при первичном анализе результатов проверки комиссией области С .

• 2.    Статистические формируются на основе оценки базовых показателей работы экспертов.

• 3.    Нормированные строятся для базовых и соответствующих им статистических оценок по множествам экспертов [3].

• 4.    Качественные представляют собой оценку параметров на основании результатов выполнения алгоритма кластеризации и нечеткого логического вывода.

• Сп исок рассматриваемых базовых показателей результатов работы экспертов представлен в табл. 1.

Таблица 1

№	Показатель	Сокращение
1	Количество проверенных заданий	ОбщЗдн
2	Количество заданий, по которым оценка (сумма баллов) расходится с результатом второй проверки	2ПрКор
3	Количество заданий, для которых была проведена третья проверка	3ПрОбщ
4	Количество заданий, по которым оценка (сумма баллов) расходится с результатом третьей проверки	3ПрКор
5	Сумма абсолютных значений расхождений с суммой баллов третьей проверки	3ПрАбсКор

Базовые показатели результатов работы экспертов

Показатель ОбщЗдн отражает объем работы, выполненной экспертом. Показатель 2ПрКор отражает количество расхождений с результатами второй проверки, но не дает возможности понять, кто из двух экспертов допустил ошибку. Показатель 3ПрОбщ отражает количество ошибок эксперта, выявленных при третьей проверке. Показатель 3ПрАбсКор определяет, насколько существенными были ошибки эксперта.

В табл. 2 представлены статистические оценки базовых показателей работы экспертов.

Таблица 2 Статистические оценки показателей работы экспертов

№	Показатель	Сокращение
1	Показатель слаженности работы экспертов	СлажГрп
2	Среднее значение расхождений при второй проверке ( Δ x 2)	2ПрСрКор
3	Среднеквадратическое отклонение балла расхождений при второй проверке	СКО2ПрСрКор
4	Частота возникновения у эксперта корректировок при вторых проверках	2ПрЧастКор
5	Среднее значение балла корректировок при третьей проверке ( Δ x 3 )	3ПрСрКор
6	Среднеквадратическое отклонение корректировок при третьей проверке	СКО3ПрСрКор
7	Частота возникновения третьих проверок у эксперта	3ПрЧаст
8	Частота возникновения корректировок эксперта при третьих проверках	3ПрЧастКор
9	Удельное значение корректируемого балла для эксперта	3ПрУдВелКор

Исходя из принятых допущений, качество работы эксперта можно оценить с помощью показателя СлажГрп , который вычисляется по формуле:

nгрп

СлажГрп = ——,                                     (3)

nгрп грп                                                                                          грп где n — общее число задач экзаменующихся, решение которых было оценено в группе эксперта; n   — число задач, оценка (сумма баллов) которых совпала с результатами второй проверки.

Показатели 2ПрСрКор и 3ПрСрКор могут использоваться при принятии решения о наличии соответствующей тенденции у оцениваемого эксперта.

Показатель 2ПрСрКор находится по формуле:

z t2 i^{A x} 2 к

2 ПрСрКор =   ^к = 1 ---i- ,                                      (4)

k где t2 — количество расхождений при второй проверке у i-го эксперта; Δx2  — расхождение выставленного i-м экс пертом балла в k-м задании по формуле (1).

Показатель 3ПрСрКор находится по формуле:

z t3 3_ ,д х з к

3 ПрСрКор = ^к = 1 ---i- ,                                      (5)

k где t3 — количество корректировок эксперта при третьей проверке; Δx3  — корректировка выставленного i-м экспер том балла в k-м задании по формуле (2).

Показатели 2ПрЧастКор , ЗПрЧаст и ЗПрЧастКор характеризуют частоту несовпадений оценок экспертов при вторых проверках, частоту возникновения третьей проверки и частоту корректировки при третьей проверке соответственно. Данные показатели находятся относительно общего числа проверенных заданий. Для определения этих показателей использовались формулы:

2 ПрКор

2 ПрЧастКор = ^ ^ ;

3 ПрОбщ

3 ПрЧаст = ^    ;

3 ПрКор

3 ПрЧастКор =

ОбщЗдн

.

Показатель ЗПрУдВелКор отражает количество ошибочно выставленных баллов, приходящееся на одно проверенное экспертом задание. Данный параметр находится по формуле:

3 ПрУдВелКор =

t 3

^ k = 1

Δ x 3 _i ^k

ОбщЗдн

,

где 1 3 — количество корректировок эксперта при третьей проверке; A x 3 k — отличие от выставленного i -м экспертом балла в k -м задании — в соответствии с формулой (2).

Для построения системы сравнения качества работы экспертов рационально использовать нормированные значения оценок — будем называть их индикаторами (имеют приставку « Инд »). Индикаторы соответствуют количественным показателям оценки эксперта. Например, ИндЗПрСрКор рассчитан для параметра ЗПрСрКор . Значения индикаторов находятся в интервале [0;1]: 1 соответствует наилучшему значению параметра, 0 — наихудшему. Рассматриваются 7 нормированных параметров: — Инд2ПрСрКор, — ИндСКО2ПрСрКор, — Инд2ПрЧастКор, — Инд3ПрСрКор, — ИндСКО3ПрСрКор, — Инд3ПрЧастКор, — Инд3ПрУдВелКор.

Показатель Инд3ПрЧастКор i для i -го эксперта находится по формуле:

max(3 ПрЧастКор ) - 3 ПрЧастКор.

Инд 3 ПрЧастКор- =------------------------------'— ,

i  max(3 ПрЧастКор ) - min(3 ПрЧастКор )

где  max(3 ПрЧастКор )

максимальное

значение показателя ЗПрЧастКор среди всех членов комиссии;

min(3 ПрЧастКор ) — минимальное значение показателя ЗПрЧастКор среди всех членов комиссии.

Аналогично равенству (10) (и при соответствующей замене показателей ЗПрЧастКор и ЗПрЧастКор ) находятся величины Инд2ПрЧастКор_i , Инд3ПрУдВелКор_i , ИндСКО2ПрСрКор_i и ИндСКО3ПрСрКор_i.

Итак, завышение или занижение баллов при оценивании заданий является отрицательной характеристикой эксперта. Предпочтительно отсутствие любого из названных недостатков. Поэтому показатели Инд2ПрСрКор_i и Инд3ПрСрКор_i для i -го эксперта рассчитываются по формулам:

Инд 2 ПрСрКор. =

Инд 3 ПрСрКор. =

max(| 2 Пр СрКор |) -12 Пр СрКор. | max(|2ПрСрКор|)-min(|2ПрСрКор|) ’ max(|3 ПрСрКор |) -13 ПрСрКор. | max(|3 ПрСрКор\) - min(|3 ПрСрКор\) ’

где _max(|2 ПрСрКор\ ), _max(|3 ПрСрКор\ ) — максимальные абсолютные значения соответствующих показателей среди всех членов комиссии; min(|2 ПрСрКор ), _min(|3 ПрСрКор |) — минимальные абсолютные значения соответствующих показателей среди всех членов комиссии.

При обосновании принятия решений по оцениванию результатов работы экспертов была применена теория нечетких множеств. Данная теория предложена Л. Заде и позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. В нечеткой логике значения любой величины представляются не чис- лами, а словами естественного языка и называются термами [4, 5]. При оценивании качества работы экспертов количественные показатели дополняются качественными оценками, выраженными базовыми и расширенными терм-множествами. Для качественных оценок значений показателей были использованы три основных терма базового терм-множества: «низкое» (низкое качество проверки), «среднее» (среднее качество проверки), «высокое» (высокое качество проверки). Также были введены четыре терма, относящиеся к расширенному терм-множеству: «скорее низкое, чем среднее», «скорее среднее, чем низкое», «скорее среднее, чем высокое» и «скорее высокое, чем среднее». Термы из расширенного терм-множества позволяют классифицировать экспертов, которые явно не относятся ни к одной из основных групп. Использовались следующие качественные параметры эксперта (имеют приставку «Оц»): — Оц2ПрСрКор,

— Оц2ПрЧастКор,

— Оц3ПрСрКор, — Оц3ПрЧастКор.

Метод нечеткой кластеризации . В качестве метода кластеризации экспертов по результатам их работы был использован алгоритм Fuzzy C-Means ( FCM) [6, 7]. Этот алгоритм чаще всего применяется для нечеткого группирования объектов. Он формирует группы, прототипы которых представляются точками в пространстве параметров кластерных объектов. Для выполнения алгоритма группировки объектов с множеством параметров A необходимо выбрать подмножество параметров объектов B с A , по значениям которых будет реализована кластеризация, определить подходящую метрику, количество групп с , степень нечеткости n , параметр ε в критерии остановки алгоритма, а также случайным образом инициировать матрицу принадлежности объектов к той или иной группе U^a ° £ Z i ( i — количество групп) и вектор прототипов V^ [8].

Были проведены эксперименты по обработке результатов проверки работ различных экзаменационных комиссий [1, 2, 10]. С помощью анализа показателей результатов работы экспертов с учетом принятых допущений установлено, что качество работы экспертов наиболее информативно отражают следующие показатели: ИндЗПрЧастКор , ИндЗПрУдВелКор, ИндЗПрСрКор и ИндСКОЗПрСрКор . Показатель ИндЗПрЧастКор представляет нормированную частоту появления ошибок у экспертов при оценивании результатов выполнения задания. Инд3ПрУдВелКор отражает существенность ошибок эксперта при оценивании. Инд3ПрСрКор оценивает наличие тенденции к занижению или завышению оценок при выставлении баллов. ИндСКО3ПрСрКор демонстрирует стабильность в принятии экспертом решения. Для наглядности было выбрано двумерное пространство параметров, построенное по индикаторам, оценивающим частоту корректировки при третьей проверке (параметр y ) и удельное значение корректируемого балла оценивания при третьей проверке (параметр x ).

В рассматриваемом двумерном пространстве координаты точки — это оценки результатов работы экспертов. Расстояние между точками может быть измерено различными метриками, которые являются формулами (правилами) для определения расстояния между любыми двумя точками заданного пространства. При выборе метрики были рассмотрены несколько возможных вариантов: расстояние Чебышева, Евклидово расстояние, квадрат Евклидова расстояния, «взвешенное» Евклидово расстояние, расстояние городских кварталов (Манхэттенское расстояние).

Для рассматриваемых параметров экспертов приемлемые результаты кластеризации были получены с применением метрики взвешенного расстояния Евклида.

Расстояние ( dist i ) от точки до центра i -го кластера находится по формуле:

dist i = 7 ^k 1 ⁽x i ^- x ⁾² + k 2 ⁽ У. ^- У ⁾² ,                                            ⁽¹³⁾

где x i , y i — значения координат центра i -го кластера; x, у — значения координат точки эксперта; k 1 , k ₂ — весовые коэффициенты.

Для каждого эксперта введем понятие нормы как взвешенную метрику (13), в которой вместо центра i -го кластера ( x i , y i ) используется точка (1,1). Будем считать, что чем ближе к точке (1,1) находится эксперт, тем лучше качество его проверки. В этом случае норма ( r ) может быть вычислена по формуле:

r = 7 k 1 (1 - x )² + k 2 (1 - У )² ,                                               (14)

где x, y — значения координат точки эксперта; k 1 , k 2 — весовые коэффициенты.

В качестве условия завершения алгоритма рассматривается малое суммарное изменение параметра dist между соседними итерациями среди всех экспертов:

Е distj -Е dist-1 <£,                                               (15)

где е — заданная константа.

Алгоритм FCM чувствителен к резко отклоняющимся значениям оцениваемых параметров — так называемым шумам или выбросам [9]. Поэтому перед применением основного алгоритма производится поиск и исключение таких точек из исходных данных. Выбросами считаются точки, которые удалены от центра группы на расстояние, превышающее удвоенное среднеквадратическое отклонение этого расстояния для точек данной группы. Начальные центры кластеров распределяются равномерно по центрам отрезков от минимального значения нормированного параметра до максимального. Центры кластеров выбираются таким образом, чтобы минимизировать суммарное расстояние от объектов группы до ее центра и максимизировать расстояние между центрами кластеров. Количество кластеров принимается равным 3 — по количеству основных групп оценивания экспертов (низкое качество проверки, среднее качество проверки и высокое качество проверки).

Начальное значение центра i -го ( i £ [1: count ]) кластера ( centr i ) находится по формуле:

max( npar ) - min( npar ) centr. = min( npar ) + i x------------------------ ,

i                        2,0 x count где min (npar) — минимальное нормированное значение параметра; max (npar) — максимальное нормированное значение параметра; count — количество кластеров.

Параметр принадлежности ( belongs ) эксперта к i -му кластеру находится по формуле [8]:

2,0

1 0 ^{n - 1}’⁰

be longs = - ------,                                                (17)

dist где disti — дистанция до центра i-го кластера по формуле (13); n — коэффициент нечеткости.

Анализ полученных результатов. Рассмотрим работу предложенного метода на примере обработки результатов проверки экспертной комиссией бланков заданий по дисциплине «Математика: профильный уровень». Комиссия состоит из 59 экспертов, количество проверенных заданий варьируется от 520 до 1462 и в среднем составляет 758.

На рис. 1 и 2 представлены графики распределения экспертов по группам с учетом шумов и без учета шумов соответственно. Эксперты с низким качеством проверки обозначены квадратами, со средним — треугольниками, с высоким — ромбами. Перечеркнутыми фигурами обозначены значения параметров экспертов, которые были приняты выбросами (шумами). Темными точками на графиках обозначены центры кластеров.

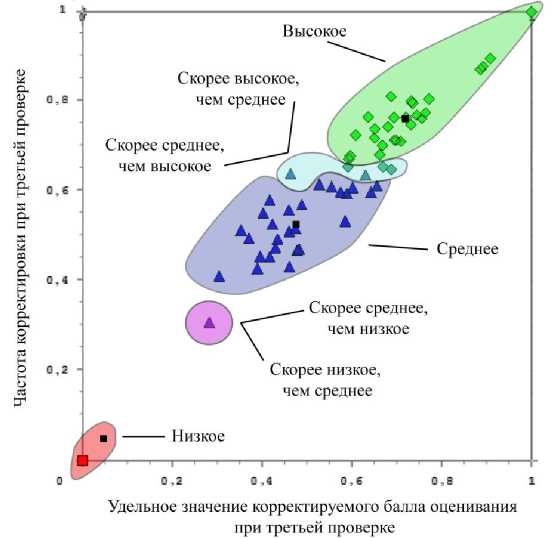
Рис. 1. График распределения экспертов на группы без учета шумов

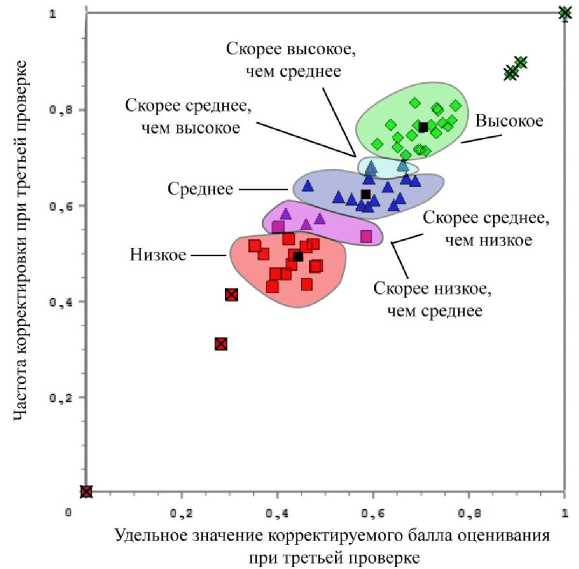
Рис. 2. График распределения экспертов на группы с учетом шумов

Как видно из рис. 1 и 2, шум оказывает влияние на работу алгоритма при нахождении центров кластеров и является причиной неточного определения качественных параметров экспертов. Неточность определения связана с тем, что шумовые значения могут полностью перетягивать на себя центры кластеров.

Оценка результатов работы комиссии приведена в табл. 3.

Оценка работы экспертов комиссии с учетом шумов

Таблица 3

№	ИН*	3ПрЧастКор, %	3ПрУдВелКор	Выс.	Сред.	Низ.	Результирующая оценка	Шум
1	1506	0,17	0,001718	1,0	0,0	0,0	Высокое	+
2	1211	0,49	0,004902	1,0	0,0	0,0	Высокое	+
3	196	0,55	0,005464	1,0	0,0	0,0	Высокое	+
4	1426	0,57	0,005671	1,0	0,0	0,0	Высокое	–
5	166	0,77	0,009615	1,0	0,0	0,0	Высокое	–
24	229	1,15	0,013436	0,37	0,63	0,0	Скорее среднее, чем высокое	–
25	185	1,16	0,015732	0,2	0,80	0,0	Скорее среднее, чем высокое	–
26	292	1,19	0,01581	0,09	0,91	0,0	Среднее	–
27	632	1,24	0,013201	0,03	0,97	0,0	Среднее	–
28	1505	1,25	0,012545	0,02	0,98	0,0	Среднее	–
38	1427	1,42	0,015986	0,0	0,99	0,01	Среднее	–
39	1425	1,46	0,021938	0,0	0,85	0,15	Скорее среднее, чем низкое	–
40	1428	1,50	0,019461	0,0	0,81	0,19	Скорее среднее, чем низкое	–
41	1507	1,53	0,020443	0,0	0,51	0,49	Скорее среднее, чем низкое	–
42	799	1,55	0,022453	0,0	0,27	0,73	Скорее низкое, чем среднее	–
43	1230	1,61	0,0161	0,0	0,16	0,84	Скорее низкое, чем среднее	–
44	163	1,63	0,021739	0,0	0,025	0,975	Низкое	–

45	633	1,66	0,019934	0,0	0,007	0,993	Низкое	–
46	289	1,68	0,020438	0,0	0,002	0,998	Низкое	–
55	646	1,92	0,020408	0,0	0,0	1,0	Низкое	–
56	638	1,94	0,022887	0,0	0,0	1,0	Низкое	–
57	215	1,99	0,025845	0,0	0,0	1,0	Низкое	+
58	245	2,30	0,026596	0,0	0,0	1,0	Низкое	+
59	1214	3,26	0,036399	0,0	0,0	1,0	Низкое	+

*ИН — идентификационный номер эксперта.

Рассмотрим пример распределения экспертов на группы с учетом шума. В табл. 3 параметры «Выс.», «Сред.», «Низ.» показывают нормированное значение отношения к кластерам высокого, среднего и низкого качества проверки соответственно. При расчетах принадлежности экспертов к кластерам был выбран коэффициент нечеткости ( n ) 1,5. Параметр «Результирующая оценка» представлен термами базового и расширенного терм-множества. Эксперты упорядочены по значению их норм (14).

Как видно из табл. 3, показатели шестерых экспертов (1506, 1211, 196, 215, 245, 1214) были приняты за шумы и исключены из алгоритма нахождения центров кластеров. Наихудшие показатели у экспертов 646, 638, 215, 245 и 1214, которые были отнесены к кластеру низкого качества проверки. Некоторые группы экспертов находятся на границах кластеров: высокого и среднего качества проверки (229, 185) и среднего и низкого качества проверки (1425, 1428, 1507, 799, 1230). Наилучшее качество проверки показали эксперты: 1506, 1211, 196, 1426 и 166, которые были отнесены к кластеру высокого качества проверки. У данных экспертов наименьшие показатели частоты корректировок при третьей проверке и удельного корректируемого балла.

Выводы. Проведенный анализ методических рекомендаций ФИПИ по проверке экзамена в форме ЕГЭ показал, что качество работы экспертов отражают следующие параметры: частота корректировки при третьей проверке, удельное значение корректируемого балла оценивания при третьей проверке, среднее значение балла корректировки и среднеквадратическое отклонение балла корректировки.

В результате проведенных экспериментов был выбран двумерный критерий оценки качества работы экспертов, с использованием которого реализовано нечеткое разделение экспертов на классы (высокое, среднее и низкое качество проверки). Оставшиеся показатели могут быть использованы для уточнения тенденции эксперта и определения его уверенности в выставлении баллов.

Разработанная методика позволяет оценить качество работы экспертов и обосновать решения о повышении квалификации членов предметной комиссии.

В соответствии с полученным распределением предлагается при формировании комиссий отказываться от экспертов, которые попали в группу низкого качества проверки. Экспертам со средним качеством проверки следует дать рекомендации, позволяющие улучшить показатели.