Метод количественного описания зависимости модуля Юнга никелида титана от температуры

В ряде работ сообщалось, что в материалах с обратимыми мартенситными переходами упругие постоянные, например модуль Юнга, сложным образом зависят от температуры [1,2]. Отмечено, что при нагревании материала через интервал обратного мартенситного перехода модуль Юнга может сильно изменяться, уменьшаясь в три–пять раз и достигая локальный минимум примерно в середине интервала обратного мартенситного перехода. В связи с этим была поставлена задача экспериментального изучения зависимости эффективного модуля Юнга от температуры.

В работе применялась экспериментальная методика, описанная в [7]. В качестве объекта исследований использовали проволоку из сплава ТН-1 с длиной 1 м и диаметром 2 мм. Характеристические температуры мартенситных переходов составляли соответственно Мн= 330 К, Мк= 290 К, Ан=340 К, Ак= 380 К. Эффективный модуль Юнга находили двумя способами: при активной изотермической догрузке и при разгрузке. В первом случае внешнее напряжение увеличивалось от 5 до 6 МПа, а во втором – оно уменьшалось от 6 до 5 МПа. Эффективное значение модуля Юнга определяли как тангенс угла, образуемого касательной к кривой и горизонтальной осью ε , что в конечных разностях можно представить согласно выражению (1)

Δ σ

Δ ε ,

где Δ σ – изменение величины напряжения, связанное с изменением нагрузки, Δ ε – соответствующий деформационный отклик.

Основные результаты экспериментов представлены на рисунках 1–2.

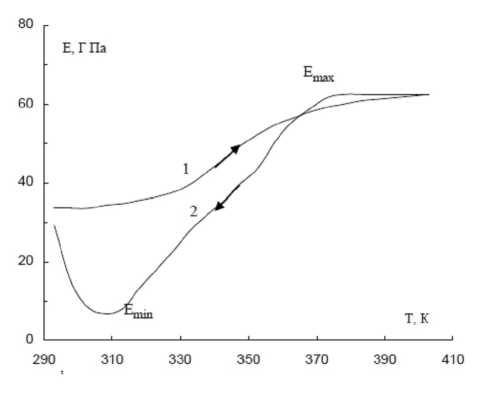
Рис. 1. Зависимость эффективного модуля Юнга, определяемого при догрузке от температуры при термоциклировании в полном интервале мартенситных переходов. Здесь и ниже стрелки обозначают направление изменения температуры.

Из рис. 1 видно, что если модуль Юнга E определять первым способом, то его величина монотонно возрастает (примерно в 2,5 раза, кривая 1) с увеличением температуры в интервале обратного мартенситного перехода. Последующее охлаждение в интервале прямого мартенситного перехода приводит к экстремальной зависимости модуля E, с достижением локального минимума при Т ≈ 305÷308 К. При этом его величина за такт охлаждения изменяется примерно в семь раз. Иная картина, если определять эффективный модуль Юнга при разгрузке (рис. 2). В этом случае E демонстрирует сложную экстремальную зависимость при нагревании с локальным минимумом при температуре Т ≈ 332 ÷ 335 К с последующим возрастанием при нагревании примерно в шесть раз. Охлаждение через интервал прямого мартенситного перехода приводит к монотонному уменьшению модуля E в интервале температур от 340 до 305 К приблизительно в два раза. Сравнение кривых на рис. 1 и 2 показывает, что при переходе от первого способа определения E ко второму кривые при нагревании и охлаждении качественно как бы меняются местами.

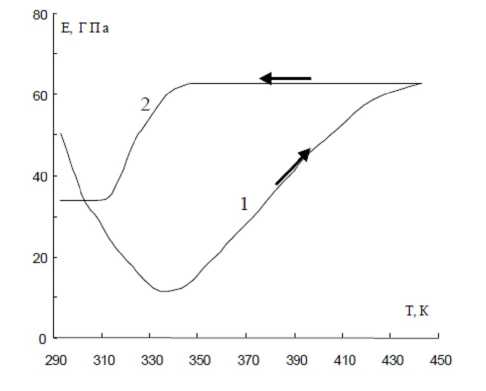
Рис. 2. Зависимость эффективного модуля Юнга, определяемого при разгрузке от температуры при термоциклировании в полном интервале мартенситных переходов.

Для численного моделирования полученных экспериментальных зависимостей предлагается использовать следующую одномерную модель мартенситной неупругости.

Дифференциал количества низкотемпературной мартенситной фазы определяется формулой dФ = н(-dT*)• H(T* - Mk) •

• H ( M k + ( M n - M k ) • arccos(2 -Ф- 1)/ п - T *) •

^П sin ( ⁿ ^ ( T * ^- M k )/( M n ^- M k ) ) /2 • ⁽ M n ^- M k ) ^- (2)

- H ( dT *) • H(T * - A n ) •

• H (T * - An - (Ak - An) • arccos(2-Ф-1)/п )• п sin (п (T * - An)/(Ak - An))/ 2 • (Ak - An)

где T ^* – эффективная температура, определяемая формулой

T * = T - C • CT ,                 (3)

C – константа материала, T и σ – температура образца и приложенное к нему внешнее напряжение, H ( x ) – функция Хевисайда.

Пластичность превращения имеет место, если

M k <  T * <  M k + ( M n - M k ) • arccos(2 • Ф - 1) / n , при этом Ф изменяется от 0 до 1 при уменьшении T ^* от M n до M k .

Эффект памяти формы имеет место, если

A_n + ( A_k - A_n ) • arccos(2 •Ф - 1) / п <  T * <  A_k , при этом Ф изменяется от 1 до 0 при увеличении T ^* от A_n до A_k .

Дифференциал фазовой составляющей деформации образца определяется формулой de6 = K • ст • dФ ,                (4)

где K – константа материала.

Упругую составляющую деформации учитываем обычным способом, полагая, что выполняется закон смеси фаз.

u Em -Ф + Ea ■ (1 -Ф) ’ где Em и Ea – модули Юнга мартенсита и аустенита.

Полная деформация образца вычислялась как сумма фазовой и упругой компоненты дефор- мации

S = ^ 5 + ^ ^{ô u} .                         (6)

При численном моделировании константы принимали следующие значения:  M n = 330 K,

Mk= 290 K, An= 340 K, Ak= 380 K. Модули упругости для мартенситной и аустенитной фаз определяли экспериментально в соответствии с форму- лой (1), что составило Em= 3,3·1010 ГПа, Ea = 6,2·1010 ГПа. Характеристические температуры мартенситного перехода и упругие постоянные аустенита и мартенсита были взяты из вышеприведенных экспериментальных данных. Численное значение константы C = 3.35·10-7 взято из экспе-

риментальных зависимостей величин характеристических температур мартенситных переходов от напряжения, при котором осуществлялось термоциклирование [5].

Константу ^K находили методом последовательных приближений. В качестве исходного приближения брали значение, найденное по экспериментальным зависимостям γ от τ из работы [6], которое составило K = 12 d Y (Тт = 2 - 10 ^{— 10} МПа \ В качестве эталонного параметра приближения принима-

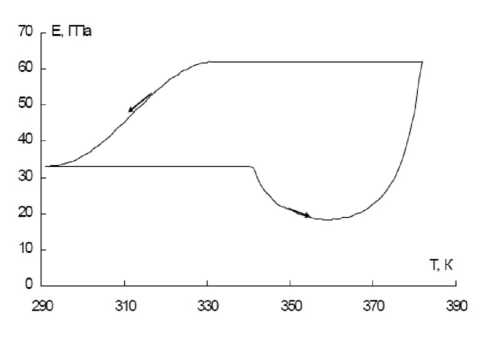
Рис. 4. Результаты численного моделирования зависимости модуля Юнга никелида титана от температуры при разгрузке.

ли величину, равную E _min

Е +Е .

min разгр min нагр

где E _{min разгр} и E _{min нагр} – минимальные значения экспериментального модуля Юнга, найденного при разгрузке и нагрузке. Расчетным путем определяли аналогичные характеристики E _{min разгр} и E _{min рнагр} – минимальные расчетные значения модуля Юнга, найденные при разгрузке и нагрузке. Точно так же находили расчетную величину

Е +Е .

min разгр     min нагр

E mi n р =----------------- . Приближения пре-

кращались, когда расчетные значения удовлетво-

ряли условию

E min р

—

E min

Е min

< 0.05.

Условие (7) выполнялось уже после пятой итерации при ^K = 10-12 МПа-1.

Результаты численного моделирования приведены на рисунках 3 и 4.

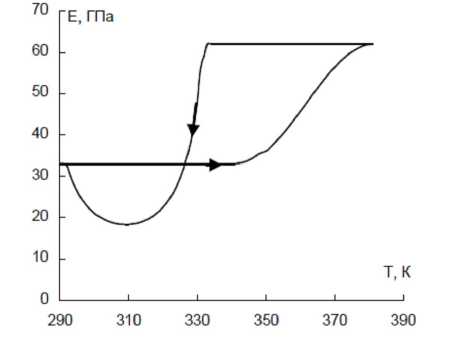
Рис. 3. Результаты численного моделирования зависимости модуля Юнга никелида титана от температуры при нагружении.

Сравнение рисунков 1–2 и 3–4 показывает, что предложенная модель мартенситной неупруго-сти удовлетворительно описывает зависимости упругих постоянных никелида титана от температуры. Это говорит о том, что предложенный аналитический подход может быть использован при определении эффективного модуля Юнга. Разработанная в данной статье аналитическая модель даст возможность более корректно ставить и точно решать краевые задачи термомеханики для материалов с памятью формы. Это позволит создать математические принципы программируемого формирования требуемых функционально-механических свойств мартенситной неупругости на элементах конструкций и изделиях с памятью формы.