Метод коллокации с бикубическим эрмитовым базисом в области с криволинейной границей

Широкое применение метода конечных элементов при решении дифференциальных уравнений с частными производными не уменьшает необходимости создания и использования новых методов, которые при более простом алгоритме реализации позволяют получить приемлемые решения с повышенной точностью.

Метод коллокации успешно применялся для численного решения краевых задач для обыкновенных дифференциальных уравнений [1] и уравнений с частными производными [2], в том числе для эллиптических уравнений второго порядка [3]. В них приближенное решение ищется в пространстве кусочноквадратичных функций на сетках с прямоугольными или треугольными ячейками. В работах [4; 5] рассматривается метод коллокации и наименьших квадратов. В работе [6] метод рассматривается в областях общего вида.

Метод коллокации с бикубическим эрмитовым базисом имеет некоторые преимущества. Так, по сравнению с методом конечных элементов Галеркина не требуется вычислять интегралы для определения коэффициентов матрицы. Для общего линейного эллиптического оператора с достаточно гладкими коэффициентами и граничными условиями Дирихле, эрмитова коллокация обеспечивает точность O( h ⁴ ) в норме L 2 , где h – шаг сетки. Эрмитовы элементы более эффективны по сравнению с лагранжевыми элементами, так как размерность систем алгебраических уравнений оказывается меньше при одинаковом порядке аппроксимации [7].

При фиксированном значении одной из переменных бикубическая эрмитова функция и ее первая производная по этой переменной превращаются в одномерные эрмитовы кубические функции относительно другой переменной [8], это дает 16 степеней свободы в каждом прямоугольнике. Стандартный базис в одномерном случае состоит из функций двух типов, интерполирующих значения функции и ее производных соответственно на отрезке [ x j , x l ]:

I 1 в узле x = x j

Ф j = <               ^J ; ш l = 0 вовсех узлах;

[0 вдругих узлах дфj                    дш, I 1 вузле x = xl;

—- = 0 вовсехузлах; —L = < дx                   дx   [0 вдругихузлах.

На эти функции натянуты все кусочно-кубические функции класса С ¹ . Эрмитово бикубическое пространство есть произведение двух эрмитовых кубических пространств, и четыре параметра в обычных узлах z = ( x j , y _l) приводят к четырем соответствующим базисным функциям:

^Ф 1 = Ф j ^{( x} ) Ф 1 ⁽ У X ^ф 2 = Ф j ^{( x} ) ш 1 ⁽ У X

^Ф 3 = V j ( x ) Ф 1 (y ), ^ф 4 =ш j (x ) ш 1 (y ).

Бикубические элементы (конечные элементы с базисом из бикубических эрмитовых элементов) применяются только на прямоугольниках (или, после простого линейного преобразования плоскости, на параллелограммах). На прямоугольной области эрмитов бикубический элемент – один из самых лучших. Его гладкость непосредственно следует из гладкости базиса. Поэтому бикубические элементы можно использовать для уравнений четвертого порядка, пробные функции будут принадлежать H ² . Эрмитово пространство S h состоит из всех непрерывных кусочнобикубических функций v , у которых v x , v y , v xy непрерывны [9].

Рассмотрим первую краевую задачу для эллиптического уравнения в области Ω:

Lu = f , x e Q , u ( x ) = 0, x e 5Q ,

где Q = {( x , y ) | x ² + y ² <  1; x >  0; y >  0}; dQ - граница;

L – линейный эллиптический оператор второго по-

( д ² u д ² u )

рядка Lu = -1 —+ I .

(д x ² д y ² J

На примере решения этой задачи рассмотрим алгоритм метода коллокации. Суть метода заключается в том, что приближенное решение ищется в конечномерном линейном пространстве функций, а неизвестные коэффициенты его разложения по базису пространства определяются из уравнений коллокации и краевых условий. Уравнения коллокаций представляют собой требования того, чтобы приближенное решение удовлетворяло уравнениям исходной дифференциальной задачи в конечном множестве точек области (точках коллокации), в которой ставится данная задача. Для получения краевых условий соответствующие условия задачи записываются в нескольких точках на границе области.

Для аппроксимации решения покроем область согласованной с границей сеткой с прямоугольными ячейками:

I               n i            . n j    .

w_h =< x = sin—, y, = sin —, j = ^h I ¹     2 N ^j 2 N

⁰ ,N,i = °_l (4)

0, N - i + 1, i = 1, N I

При этом ячейки сетки делятся на внутренние (регулярные), которые не содержат границы области, и граничные (нерегулярные). Сетка согласуется с границей так, чтобы два узла в нерегулярных ячейках лежали на криволинейной границе. Это позволяет уменьшить общее количество базисных функций в области. Общее число ячеек на такой сетке равно

= N ( N + 1).

el 2

В качестве базисных функций в каждой ячейке задаются бикубические многочлены Эрмита с 16 степенями свободы. В области [–1,1]×[–1,1] они определяются следующим образом [10]:

ф i ⁽ z i ) = ¹ , Ф / C z j ) = 0, i * ^j ;

дф /(Zi ) 1 дФ xi (zj) A ..

^xi i = 1,-------— = 0, i * j ;

дxд дФ yi( zi) , дФ yi(zj) „ ..

—^y— = 1, — ^y—— = 0, i * j ;

дyд д2Ф xyi( zi) , д 2Ф xyi(zj) „ ..

---y— = 1, —y—— = 0, i * j, дx дy        дx дy дф xyi (zj) = 0,дф xyi (zj) = 0, i, j = 1,2,3,4.

д x          д y

Для каждой ячейки точки коллокации берутся в нулях полинома Лежандра

P2 I^yx—xi—xi-L|, чтобы ( xi- xi-1 J достичь наибольшей возможной точности [11]:

^i,m = xc,i ± "6" hx,i, ^ym = Ус,J ±    hy, j, m = 1,2, где    xc,i

x + x - 1 „ _^yj + yj - 1

2    , y c , j =      2

h x , - = x ^- x - 1 ,

h y , j = y j - y j - 1 , i = 1, ..., k , j = 1, ...,l.

При этом для прямоугольной области верна оценка || u - uh^ <  Ch⁴ ||u||H 4 (_П) [12], где H m ( Q ) обозначает пространство Соболева с нормой

II v l H m ( Q )

. 2

0 < - + j <  m

d ^{- + j}v d x^- d y^-

2     12

L 2 ( Q ) у

Оценки в других нормах даны в работе [13].

В каждой граничной ячейке добавляются по 3 точки коллокации равномерно на границе:

^ x_{u 4} = cos —[- + 1 , ^- , ^{k + 4}        ( 2 N ( 4 JJ

§ ^y _{jfc+ 4} = sin |—^f j + 1| , k = 1,2,3. j , ^k I 2 N I     4 J J

При такой расстановке общее число точек коллокации совпадает с общим числом базисных функций с учетом граничных условий и равно N _ф = 2 N ² + 5 N . На рис. 1 изображена построенная сетка с точками коллокации. Узлы сетки обозначены жирными точками, точки коллокации – крестами.

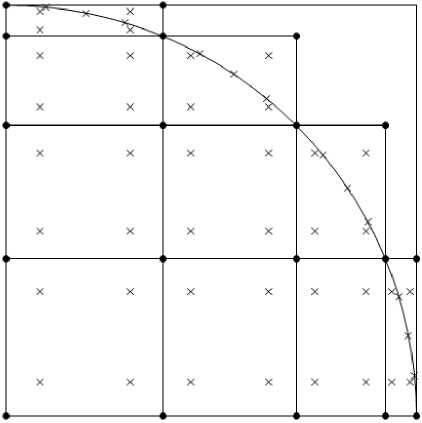
Рис. 1. Согласованная сетка и точки коллокации

Построенный метод коллокации аппроксимирует неизвестную функцию u функцией U в пространстве конечномерных функций V . В построенном базисе эрмитовых бикубических функций функция U равна:

u h ( x , y ) = 2 u h Ф _n ( x , y ),               (6)

n = 1

где Ф _n - эрмитовы бикубические базисные функции; n G – число точек коллокации; U n – коэффициенты.

Задача эрмитовой коллокации состоит в том, чтобы найти U е V , удовлетворяющее (1) в точках коллокации, т. е.:

Lu^h (^ , ^ y ,_m ) = f (^m , ^ y ,_m ) , ()£„ , ^ y ,_m ) eQ ; 7 U h ( ^ x m , ^ y ,m ) = 0, ( ^ x m , ^ y m ) е dQ .

Решение задачи сводится к решению линейной системы Au = f , где элементы матрицы

A _{[ -} j ij ^{L Ф} j ⁽ x - , y - ) , ⁽ x - , y - ^)eQ

, J [Фj (x-,y-),(x-,y- )edQ

вектор правой части f [-"] = f (x-, y-), (x-, y- )eQ 0, (x-, y- )edQ

Для исследования порядка сходимости приближенного решения U(x,y) к точному проведены расчеты на последовательности сеток при h→0. В табл. 1 приведены результаты численных экспериментов с решением u (x, y ) = sin (1 - x2 - y2) xy,              (8)

которое удовлетворяет уравнению Пуассона (3) с правой частью f (x, y) = 4xy(3cos(1 - x2 - y2) - (x2 + y2) sin(1 - x2 - y2)).

Таблица 1

Значения погрешности в норме L ₂

N	N el	N φ	max	5 й = u - u h	δ 2 h /δ h	log 2 (δ 2 h /δ h )
3	6	33	0,5	4,93 x 10 - 4
6	21	102	0,2588	2,25 x 10 - 5	21,9	4,45
12	78	348	0,1305	1,18 x 10 - 6	19,1	4,25
24	300	1272	0,0654	6,32 x 10 - 8	18,7	4,22
48	1176	4848	0,0327	3,53 x 10 - 9	17,9	4,16

Численные эксперименты с другими функциями, удовлетворяющими граничным условиям, свидетельствуют о том, что порядок сходимости приближенного решения к точному при h →0 здесь не хуже 4. Порядок сходимости α вычисляется методом наименьших квадратов из || u - u h^L <  Ch max || u|| H 4 _(Q) , где h max -максимальный линейный шаг по всем ячейкам сетки (табл. 2, рис. 2).

Таблица 2

Порядок сходимости для различных функций

Функция	Порядок сходимости α
u 1 = sin ( 1 - x 2 - y 2 ) xy	4,2779
u 2 = ( 1 - x 2 - y 2 ) sin ( nx ) sin ( n y )	4,2169
u 3 = ( ( 1 - x 2 - y 2 ) xy )	4,4270
u 4 = ( 1 - x 2 - y 2 ) sin ( xy )	4,3803
( 1 - x 2 - y 2 ) xy     , u 5 = ev        1 - 1	4,3953

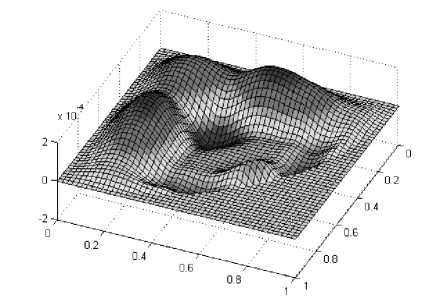
Рис. 2. Распределение ошибки при разбиении на 10 ячеек

Результаты численных экспериментов показывают, что данный алгоритм обладает сходимостью повышенного порядка. Согласование узлов ячеек расчетной области с областью определения задачи позволяет увеличить теоретический порядок сходимости метода и уменьшить размерность пространства базисных функций. При этом по сравнению с методами Галеркина и Ритца метод коллокации более прост в реализации, так как нет скалярных произведений, а значит, не нужно интегрировать. Вместе с этим эффективно используются бикубические эрмитовы базисные функции, так как по сравнению с лагранжевыми они показывают больший порядок аппроксимации.