Метод контроля плотности жидких сред по спектральным характеристикам отраженных акустических импульсов

цов волноводов 1 и 2 устанавливается зеркальная пластина 4 для отражения импульсов из горизонтальной плоскости распространения в вертикальную и обратно. Между открытым концом волновода 1 и отражающей пластиной 4 существует технологическое отверстие, предназначенное для свободного хода продукта в полости волноводов. Генератор 5 выдает зондирующие импульсы на акустический датчик 3, вернувшийся отраженный сигнал принимается также датчиком 3 и передается в устройства 6 и 7 для определения времени распространения импульса в полости волноводов, а также проведения спектрального анализа. Устройство позволяет:

• -    осуществлять комплексные измерения уровня и плотности жидких сред, находящихся в резервуаре,

• -    устранить проблему получения неточных данных при наличии пены на поверхности продукта,

• -    уменьшить возможность загрязнения датчика,

• -    учесть влияние “мёртвой” зоны акустического датчика.

Предлагается использовать для контроля плотности отражающей поверхности метод импульсного акустического зондирования. Сущность импульсного зондирования состоит в следующем. Посредством применения акустического датчика в направлении контролируемой среды излучается зондирующий импульс p(0,t) , (точка излучения принимается за начало координат). Дойдя до границы раздела сред, при этой пройдя расстояние Н , импульс искажается за счет свойств среды распространения (среда I) и преобразуется в импульс p(H,t) . Этот импульс частично отражается от поверхности раздела, частично преломляется, проходя в контролируемую среду (среда II), таким образом, разделяясь на два импульса: p₁(H,t) и p₂(H,t) . Эти импульсы, искаженные по форме и амплитуде относитель-

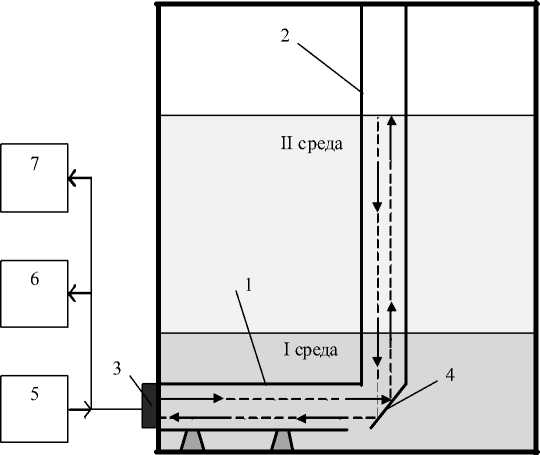
Рис. 1. Конструкция устройства для акустического контроля:

1, 2 – волноводы, 3 – акустический датчик, 4 – зеркальная пластина, 5 – генератор зондирующих импульсов, 6 – блок измерения времени, 7 – блок спектрального анализа

но зондирующего импульса, несут в себе информацию свойствах контролируемого продукта, в том числе и плотности.

В рамках математического моделирования процедуры контроля плотности приняты следующие допущения.

• 1.    Контролируемая отражающая среда однородна, изотропна и стационарна с точки зрения электрических параметров.

• 2.    Среда линейна и пассивна с точки зрения электромагнитных свойств.

• 3.    Распространение акустических сигналов происходитв полости одномерного волновода, то есть энергия в нем (вектор Пойтинга) распространяется вдоль одной координаты z .

Зондирующий импульс любой формы p(0,t) представляет собой сгусток энергии, возбуждающий вокруг себя набор колебаний разных частот, комплексный амплитудный спектр которых определяется преобразованием Фурье [2]:

∞

S (0, j®)= J p (0, t) e- j".

-∞

где z_I

В работах [4, 5] на основе теоретических положений, изложенных в [1-3] показана общая математическая модель распространения импульсов в однородных стационарных средах Спектральная плотность отраженного от контролируемой среды сигнала, прошедшего расстояние 2 Н (от точки излучения до границы сред и обратно), S(2H, jω) определяется по выражению:

S (2H, j®) = K(j®)S (0, j®) e-j2k 1j)H ,(2) где K(jщ) – коэффициент отражения, k (j®)=®1 - j^®)       (3)

cρc

– волновой вектор среды, где с – фазовая скорость звука,

• r плотность среды,

• 4 С

• ^b = - n + Z + ^C P^V      (4)

PV

– диссипативный коэффициент, где h, z, x , С _Р ,C _V – динамическая вязкость, вторая вязкость и коэффициент теплопроводности среды, удельные теплоемкости среды в изобарном и изохорном процессах соответственно.

Коэффициент отражения определится как [3]:

K(jw) = ^zi.^(j ® ) ^- z i ^(j ® )    (5)

zn(j ® ) ^{+ z}i(^j ® ) ’

^ρ I^2сI^{3                  ρ} I²I ^сI³I

2             , z u 2              ^,

ρ_Iс_I - jb_Iω       ρ_IIс_II - jb_IIω

zI , zII – акустические импедансы контактирующих сред, cI,cII,ρI,ρII,bI,bII – скорости звука, плотности и диссипативные коэффициенты контактирующих сред.

Скорости звука c_I , c_II в средах могут быть представлены как полиномиальные зависимости от плотности и в общем виде определяться выражением:

n c = f(P) = Ё akp .       (7)

Данные о плотности отражающей поверхно- сти заключены в выражении для акустического импеданса среды в соответствие с (6). Преобразуя (5), получим выражение:

z. x         X К( № ) + 1

zn(Jto) = zi(Jto) , „ , . . . (8) 1 - K( jω)

Если не учитывать поглощение сред ( b=0 ), тогда (8) примет вид:

K + 1 си ^p II = с I ^pI ~,   77 .

1 - K

Выражаем из (2) коэффициент отражения K(j ω ) , а также с учетом (7) представляя скорости звука как функции плотности f₁( ρ _I),f₂( ρ _II) , получим:

^р( P ii ) P ii = ^f( P i )P i

Sl(2H,J^) + e-.

S(0,jω)

_e ^{- 2 j} f1(^ωρI)^H _- S 1 (2H, jω) . (9)

S(0, jω)

При учете поглощения сред для расчета зависимости плотности среды II, получим, что выражение (9) имеет вид:

S№Je) + e - j-clPTH

C11P11   _   C2p2   . S(0jto)_____________ (10)

с I²I ρ II - jb II ω с I² ρ I - jb I ω - jω^2cI _c ^ρ_I2_I^I_ρ ^- _I^jbIH _S1( _{2H, j}ω) ^.

e           S(0,jω)

Рассмотрев скорость звука как функцию плотности, имеем:

⁽ f 2^{( P} II⁾ ) ^P II

( ^f2^{( P} Ii) ) ^P II - ^JbII ^to

_{- j ω} 2f 1 ( ρ I ) ρ I - jb I _H

,      ^{( f} 1 ⁽ P I ) ) ² Pl

⋅

S i (2H,Jg) + e S(0,jω)

2 f1 ( ρI )ρI - jbI - jω e      fi(PI))2 Pi

^H S 1 ( 2H, jω)

-

_ ( f i ( P i ) ) p

⁽ f i⁽ P i ) ) 2 Pi - Jbto

S(0,jω)

Полученные выражения включают в себя спектральные плотности S(0,j ω ) и S(2H,j ω ) , которые являются комплексными числами. Для дальнейшего анализа удобно с учетом формулы Эйлера представить их в показательной форме следующим образом:

S(0,Jto) = A(0,to)eJ^0m),       (12)

S(2H ,Jto ) = A(2H ,to )е]ф2н,°).(13)

Выразив отношение спектральных плотностей S(0,j ω ) и S(2H,j ω ) из выражения (2), (12), (13), получим выражения:

S(2H'J^) = K(i® )e-*"')2H (14)

S(0, ω)S(2H, J to ) _ A(2H'to)eP<2H^”)S(0,Jto) " A(0'to)e^(0to) . (15)

Приравняв выражения (14) и (15), получим:

A(2H,ω) A(0,ω)

e - k 1 ( ω )2H

e(^(2H,to) -ф(0ДО)) _ K(Jto)

При рассмотрении случая, не учитывающего поглощения сред, в выражении (16) отношение модулей спектральных плотностей зондирующе-

A(2H,ω)

го и отраженного сигналов          и модуля

A(0,ω)

коэффициента отражения K( ω ) определяют действительные части спектральных плотностей, а показатели степени е – их мнимые части. Поскольку комплексные числа равны в том случае, если равны их действительные и мнимые части, получим выражение, определяющее модуль комплексного коэффициента отражение через отношение модулей спектральных плотностей зондирующего и отраженного импульсов:

A(2Hto) _ K( Jto)|A(0,ω)            ,

Тогда согласно (16) и (17) получим выражение, определяющее зависимость плотности отражающей среды от отношения модулей спектральных плотностей контролируемых сигналов без учета поглощения сред:

A (2 H , to ) + 1

A (0, to )              |K ^{( to )}|⁺ 1

с " ^P" = ^{Ci P i} ₁ A (2 H , to ) = ^{Ci P i} T — K ( to )| '⁽¹⁸⁾

A (0, to )

Если представить скорости звука в средах как функции плотности, выражение (18) примет вид:

I K ( to )| + 1

f - ⁽ P ii ) P ii ^_ f l ⁽ P i ^)pi 1 - K ( _to )| .   (19)

При известных параметрах среды I, правая часть выражения (19) сводится к действительному числу, а левая будет представлять полином степени ( k+1 ), где f₂( ρ _II ) определяется в соответствие с (7). В простейшем случае, когда f 2 ( P ii ) _ ^ 1 "  P ii + a o — линейная зависимость с коэффициентами a₀, a₁ , выражение (19) будет представлять собой квадратное уравнение относительно ρ _II . В таком случае выражение для плотности контролируемого продукта с_II из (19) определится как:

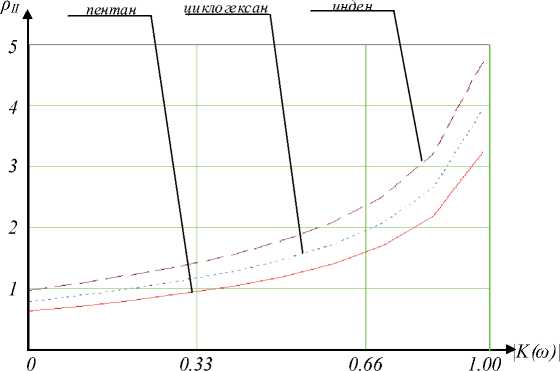
Рис. 2. График зависимости плотности отражающей среды от модуля комплексного коэффициента отражения

K (to) + 1 ’1 1 - K(to)

^- a о ⁺ a ^{2 +} 4 a i • ^f _x ⁽ p,^p

pII =

2 a 1

. (20)

Пример расчета зависимости плотностей отражающих сред от отношения модулей спектральных плотностей зондирующего и отраженного импульсов представлен на рис. 2. Показаны три варианта зависимостей для различных сред распространения зондирующих импульсов: пентан ( с=0,6263 кг/м³ ), циклогексан ( с=0,8109 кг/м³ ), инден ( с=0,9638 кг/м³ ).

Выражения (1) - (20) определяют общую методику контроля плотности жидких сред в резервуарных парках. На практике, данная методика наиболее эффективна применима, когда плотности контролируемых сред ρI , ρII соизмеримы, тогда коэффициент отражения зондирующего импульса есть значение из интервала (0,1). Пример такого случая, измерение плотности продук- та, находящегося над уровнем подтоварной воды в резервуаре. Также метод может быть применен для решения задач химической промышленности, связанных с работой с многофазными растворами и другими жидкими средами.