Метод контроля температуры при исследовании упругих свойств материалов с кристаллической микроструктурой в статическом подходе при дискретно-атомистическом моделировании

(статические) упругие модули. Использование статической постановки [4-5] позволяет получать изотермические упругие модули без расчетов переходных процессов к термодинамически равновесному состоянию. Главным недостатком статического подхода является невозможность задания температуры системы, связанной с кинетической энергией движения атомов. В работе применяется способ контроля температуры в статической постановке [3-4]. Рассматриваются идеальные монокристаллы с кубической симметрией, силы взаимодействия атомов – парные и центральные, задаваемые для примера потенциалом         Леннард-Джонса         [1-3]

^ф( r 2 ) = Р[ ( ^а/ r ) - ² ( ^а/ r ) J , где r - расстояние между взаимодействующими атомами, α – равновесное расстояние изолированной пары атомов, β - «глубина» потенциальной ямы парного взаимодействия. Полная потенциальная энергия системы есть

M - 1 M

• ф=ё£ф( rj • rj)

• ¹    = 1 j =^{1 + 1}                  ,                 (1)

где M – полное число атомов, r ij ≡r i – r j , r i – радиус-векторы атомов.

Задание температуры в статическом подходе. Атомы в твердых телах участвуют в хаотическом тепловом движении, совершая колебания вблизи положений равновесия. Температура системы атомов согласно молекулярнокинетической теории есть мера осредненной кинетической энергии их теплового движения. Пусть ri – радиус-векторы равновесных положений атомов, а hi – векторы отклонения от положения равновесия. Если θ – температура системы атомов, то

Mm^ •hi/2)i=T;M te[0,T]

где mi – масса i-го атома системы. Осреднение ^ -^ ведется по всем атомам тела и по достаточно большому промежутку времени T, в течение которого температура не меняется. При mi =m=const, получим 9~(hz •h^^i^ • Для зада- te[0,T]

ния температуры в статическом подходе принимается гипотеза:

H1. Тепловые колебания атомов кристалла являются дополнительной независимой степенью свободы и подчинены гармоническому закону с одинаковой для каждого атома амплитудой.

Эта гипотеза соответствует гармоническому приближению, справедливому для не слишком высоких температур. Пусть ω i – частота колебаний i -го атома, A – амплитуда. Осредняя по интервалу времени T, получим (h j • h j ) _te[₀,_T] ~^²w² то есть 6~Л ² ш 2 где to = ^ to ,² ^ ~^ - «эффективная» частота колебаний атомов, относительно которой делается предположение:

H2. Эффективная частота колебаний атомов кристаллической решетки не зависит от их амплитуды.

Температуру системы атомов в статическом подходе будем вводить с помощью амплитуды случайных смещений атомов:

0 = у A A

,

где γ – параметр материала, подлежащий идентификации. Фактически каждому значению температуры соответствует семейство возмущенных состояний системы атомов, представленное совокупностью всевозможных конфигураций атомов, колеблющихся с заданной амплитудой, во всевозможные моменты времени. Зафиксированная в случайно выбранный момент времени t е [ ^0, T ] конфигурация r , = R , + h , является элементом этой совокупности. Каждый такой элемент может быть реализован с некоторой вероятностью. Относительно h i делается предположение:

H3. Случайные смещения атомов h i независимы, их направления равновероятны, а модули подчинены закону распределения

' 0,   h <- A;

F ( h ) = ¹ arcsin( h A) +1/2,

1, h >  A .

- A <  h <  A ;

Функция F(h) описывает вероятность обнаружения гармонического осциллятора в некотором положении x>h в случайно фиксируемый момент времени t ^e [ 0, ^T ] (в пределе при T ^^ ).

При увеличении амплитуды колебаний атомов кристалла растет его потенциальная энергия и происходит увеличение межатомных расстояний в состоянии термодинамического равновесия – решетка кристалла при нагревании расходует часть подводимой к ней тепловой энергии на совершение работы по расширению, переходя в энергетически более выгодное состояние. Устойчивое термодинамическое равновесие системы отвечает минимуму свободной энергии F = U – θS Гельмгольца, что при условии постоянства температуры θ( A ) и энтропии S ( A ) соответствует минимуму внутренней энергии U=U kin +U pot , где U kin – кинетическая энергия тепловых колебаний, U pot – потенциальная энергия. Осредняя U по большому интервалу време ни, получим U\^_T ] = UJ_km \_e [ 0, _T ] + UJ_pot )t _e [ 0, _T ] , где Ul n^t _e[ _{0 T} ] ( 0 ) есть функция температуры, значение которой задано для рассматриваемого состояния. Тогда термодинамическое равновесие соответствует минимуму средней потенциальной энергии pot)t_e[₀,r][^(•D], представляющей собой функционал совокупности траекторий атомов системы, то есть траектории !/<(•)! конфигурации при тепловом движении. Относительно траектории, минимизирующей энергию, делается предположение:

H4. В конфигурациях термодинамически равновесной траектории системы значения периода кристаллической решетки доставляют минимум текущим значениям потенциальной энергии системы.

Для произвольной скалярнозначной функции f ( K ) конфигурации K ее осредненное по времени значение

т

>_t e[i,r] К»= ^ J f(Kto)dt

О совпадает с математическим ожиданием этой функции от траектории [K(^)] выбранной конфигурации, фиксируемой в случайный момент t ^G [ ⁰, ^T ] , то есть случайной величины K: ( ^f\ _{е [ 0} , _t ] = E [ f ( ^K ) ] . ^Эмпир^{ической} состоятельной оценкой математического ожидания является выборочное среднее, следовательно,

1 m кf\4о,ri < m7   — Z f (Kk), где Kk - незави-

■                 m k =1

симая повторная выборка реализаций случайной конфигурации K, m - объем выборки, P - вероятностная мера. При оценке (f \е[0,т] вместо fKk) удобно использовать реализации случайной величины fk с более простой зависимостью от K. Эта величина должна обладать одинаковым с f(K) математическим ожиданием, оценку которого далее будем обозначать просто как f, где

m

=1Z

m k = 1

Пусть a - равновесный период решетки невозмущенной конфигурации (A=0), а к - от- ношение к нему равновесного периода в возмущенной (A>0), то есть коэффициент температурного расширения. В соответствии с гипотезой H4, параметр к в каждой реализуемой конфигурации равновесной траектории определяется из условия минимума энергии (1). Для потенциала Леннард-Джонса из определения (1) значение к равно свойств идеальных монокристаллов с гранецентрированной (ГЦК) и объемоцентрированной (ОЦК) кубическими решетками. Образцы в форме куба содержат ne атомов на ребре. Для различных ne вычисляются равновесный период решетки и удельная потенциальная энергия ф=Ф/(nea)3. Зависимости a(ne) и ф(ne) от числа атомов аппроксимируются методом наименьших квадратов функциями из семейства fne)=c3(ne+c 1)c2+c4. Их предельные значения при ne^w являются оценками макроскопических параметров равновесного состояния (табл. 1). Получено, что размер представительного объема соответствует значению ne=30. Дальнейшие расчеты проводятся только на таких образцах.

Таблица 1. Макроскопические значения равновесных параметров

Параметр	Тип решетки
	ГЦК	ОЦК
( а/ a ) 6	0,149	0,567
Ф/Р	-34,44	-16,473

к = а

(М - 1 М     „  /М - 1 М

ZZк»I  ZZЫ у i=1 j= i+1           / i=1 j=i+1

I -(

X 1/6

- 6

7

Равновесный период a и полная потенциальная энергия Ф в невозмущенной конфигурации при P j = Р i - Р j , Р i = R i / а выражаются как

7 М - 1 М         /М - 1 М

-(

X 1/6

- 6

a = а

,

ZZк.I  ZZкj у i=1 j=i+1           / i=1 j=i+1

ф = в

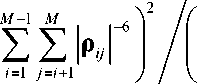
М - 1 М

ZZ Ы i = 1 j = i + 1

Для оценки упругих модулей рассматривается чистое растяжение-сжатие и простой сдвиг. Используется несимметричная форма закона Гука, обладающая материальной индифферентностью при малых искажениях _о = C : ( F - 1 - w # ) , где w # — кососимметричный тензор малого поворота кристаллической решетки. Мера деформаций f - i - _w# соответствует мере, предложенной в [8] для больших деформаций. Тензор C для материалов с кубической симметрией имеет 4 независимые ненулевые компоненты:

С С

1111 ^1122 ^,

С С

1212 ^1221

Изменение упругих модулей при нагреве образца. С помощью предложенного метода контроля температуры в статическом подходе исследуется изменение при нагреве упругих

Компоненты (4) - это функции случайной фиксируемой конфигурации K и выражаются с помощью (1-2) в базисе кристаллографических осей { x ; y ; z } как

М - 1 М                             М - 1 М

( n e ^к a ) С 1111 ( K ) = Z Z [ ² ф ( r ij ² ) ^{+ 4} x j V( r j ² ) ] + ² Z Z ^xij M r ij ² ) i = 1 j = i + 1                                                    i = 1 j = i + 1

,

М - 1 М                            М - 1 М

( n e ^к a )³ C 1122 ( ^K ) = Z Z [^ ( r j ² ) ^{+ 4} x j ⁴ ф"( r j ² ) ] ^{- 2} Z Z ( x j ^{2 +} У У ² ) V' ( r ij '² ) i = 1 j = i + 1                                                 i = 1 j = i + 1

М - 1 М

( n e ^к a ) C 1221 ( ^K ) = Z Z [ ⁴ x ij ² У Ц ² ^"( r ij ² )

i = 1 j = i + 1

( n e К a ) 3 C ₁₂₁₂ ( K ) = ( n e K a )³ C ₁₂₂₁ ( K ) + 2 У У x j ² ф‘( r j ² )

i = 1 j = i + 1

, где rjj = {Xj; у-; z- }. Упругие модули находятся как математические ожидания этих функций в равновесных конфигурациях, соответствую- щих минимуму полной потенциальной энергии (1), условие которого принимает вид

M - 1 M              M - 1 M              M - 1 M

У Ух..² ф'( г^УУ Уу²<р‘( г² У У У z² ф’Г г² У о

Z—i Z—i у Ф j ) 2—1 2—1 yj Ф i/ / Z—i 2—1 у Ф у i=1 j=i+1                        i=1 j=i+1                        i=1 j = i+1

Так как направления случайных смещений каждого атома равновероятны, а конфигурации их равновесных положений кубически симметричны, то все слагаемые этой суммы имеют один и тот же закон распределения и каждое из них должно иметь равное нулю математическое ожидание:

₃             M - 1 M

(neКa) C1111 (к) = У У [2ф(rj2 ) + 4xj4ф"(rj2 )]

i = 1 j = i + 1 ^,

M - 1 M

( n e ^K a ) C 1122 ( к ) = У У [ф ( r ij ² ) ^{+ 4} x j ⁴ ф" ( r j ² ) ]

= 1 j = i + 1 ^,

M - 1 M

⁽ n e ^K a ) ^C 1221 ( к ) = ⁽ n e ^K a ) ^C 1212 ( к ) = У У |^⁴ x j y j Ф ⁽ r ij ) ]

i = 1 j = i + 1

следовательно, тензор C сохраняет симметрию при нагреве образца.

а)

б)

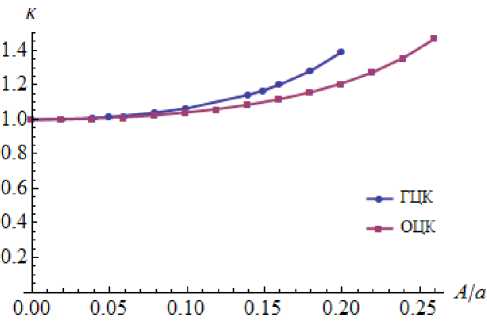
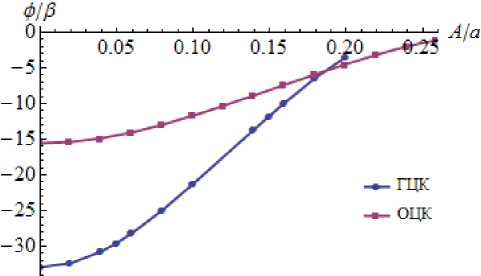
Рис. 1. Зависимость а) коэффициента температурного расширения к, б) удельной потенциальной энергии от амплитуды тепловых колебаний

Результаты и их обсуждение. Для вычисления введенных параметров генерировалась выборка из 1000 случайных конфигураций представительных образцов для каждого значения A . Зависимость коэффициента температурного расширения к от безразмерной амплитуды A / a колебаний атомов показывает монотонный рост (рис. 1, а).

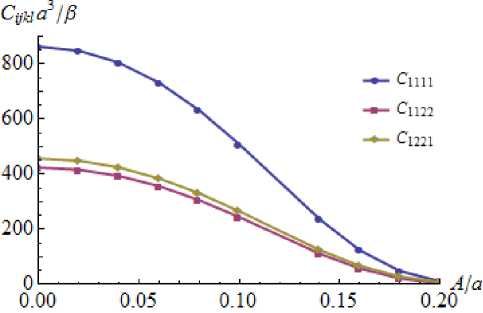
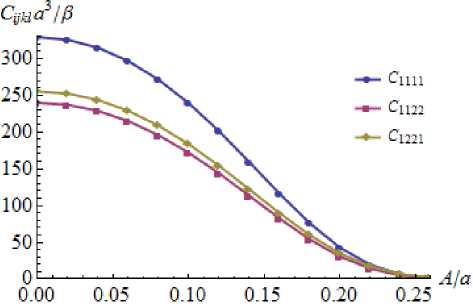
Зависимости безразмерной удельной энергии ф/в для ГЦК- и ОЦК- монокристаллов имеют общую точку (рис. 1б), позволяющую оценить температуру полиморфного превращения, как перехода в энергетически более выгодное состояние. Показано, что упругие модули при нагреве уменьшаются (рис. 2). Полученные кривые пресекаются в некоторой точке A _m , где упругие модули обращаются в ноль. Возможно, эта точка связана с температурой плавления материала. Зная ее значение 9 _m из экспериментов для конкретного материала, можно оценить параметр γ из соотношения (2): Y=9 _m / A _m ² .

Выводы: предложенный вычислительностатистический подход контроля температуры при исследовании кристаллических образцов конечных размеров с кубическими решетками в статическом подходе позволил найти изменения коэффициента температурного расширения, а также удельной потенциальной энергии и значения упругих модулей при нагреве тела. Упругие модули при нагреве уменьшаются, происходит вырождение анизотропии материала. Показано, что кривые, отражающие зависимости удельной потенциальной энергии образцов от температуры, построенные для ОЦК- и ГЦК- монокристаллов макроскопических размеров, имеют точку пересечения, соответствующую полиморфному превращению.

а)

б)

Рис. 2. Зависимость упругих модулей от амплитуды тепловых колебаний атомов: а) ГЦК-решетка, б) ОЦК-решетка

Работа выполнена в рамках задания № 2014/152 на выполнение государственных работ в сфере научной деятельности в рамках базовой части госзадания Минобрнауки РФ (код проекта 1911) .