Метод коррекции искажений волнового фронта в системе атмосферной оптической связи с малым объемом передаваемой по служебному каналу информации

В настоящее время оптические пучки с орбитальным угловым моментом получили широкое распространение в атмосферных системах связи [1], поскольку с их помощью достигается высокая плотность кодирования [2, 3]. К сожалению, из-за наличия атмосферной турбулентности [4, 5] такой способ кодирования применим лишь для небольших расстояний между приемником и передатчиком. Тем не менее, большое число статей посвящено разработке различных адаптивных систем коррекции искажений в условиях сильной турбулентности. Например, в работе [6] авторы с помощью достаточно сложной оптической схемы с обратной связью достигли ошибки передачи бита не более 10–3 при отношении сигнал / шум 15,5 дБ.

Основная задача адаптивной корректирующей системы заключается в вычислении маски фазового транспаранта по результатам измерения распределения интенсивности излучения от опорного источника [7]. Маску обычно вычисляют различными итеративными методами, а также в последнее время получили развитие методы коррекции, основанные на машинном обучении [8, 9]. Так, например, в работах [10, 11] фазовая маска строится глубокой нейронной сетью. Такой подход удобен тем, что он быстрее итеративных способов и для решения задачи не обязателен мощный опорный источник, так как может использоваться изображение, формируемое на приемнике сиг- нальным лучом. Однако в этом случае требуется передавать это изображение от приемника к передатчику по служебному каналу.

Чтобы уменьшить объем передаваемых по служебному каналу данных, можно использовать архитектуру сети, схожей с автоэнкодером. Особенностью этой архитектуры является наличие узкого «бутылочного горлышка» – скрытого слоя с небольшим количеством узлов. В таком случае задача сети заключается в том, чтобы описать изображение малым числом параметров, а затем по ним построить корректирующую маску. В итоге после обучения сеть можно разделить на две части: первая находится на стороне приемника, и информация с ее выхода отправляется на передающую сторону, где вторая часть сети, используя эти данные, управляет компенсирующим транспарантом.

Метод

Рассмотрим предлагаемый метод на модели атмосферного оптического канала связи (см. рис. 1). Гауссов пучок G (x, y, w0) с радиусом w0 =20 мм проходит через пространственный фазовый модулятор размером M ×M ячеек (M = 64). Параметры пучка выбраны таким образом, чтобы он занимал как можно большую площадь модулятора. Координаты x, y заданы на равномерной прямоугольной сетке с пространственным шагом дискретизации Δ = 1 мм. Фазовая маска θ (x, y) модулятора является суперпозицией двух мод с противоположными значениями углового орбитального мо- мента l: θ (x, y) = arg [exp (– ilψ) + exp (ilψ)], где ψ – азимутальный угол. Такая фазовая маска формирует изображение, состоящее из чередующихся темных и светлых пятен, число которых пропорционально l.

Распределение интенсивности излучения на приемнике рассчитывается в параксиальном приближении:

I ( x,y ) -F ¹ { U ( k x , k y ) x

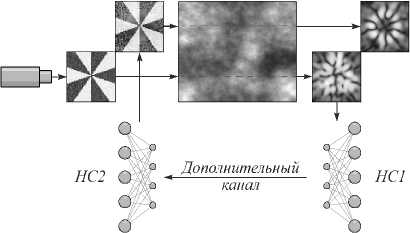
Рис. 1. Схема работы метода коррекции искажений в турбулентной атмосфере. Нейронная сеть НС1 преобразует информацию об искажениях распределения интенсивности на фотоприемнике в малый набор параметров. Эти параметры передаются по служебному каналу к источнику излучения где НС2 по ним строит корректирующий транспарант

X F { G ( x,y,w 0 ) e^{i ф}( ^xy ) e^ ^x ' ^y ) }}| 2 .

Здесь введено обозначение:

U ( k_x , k_y ) = exp I - iz ₀

k x + k y )

2 k 0² )

Атмосферная турбулентность имитируется стохастическим фазовым экраном в соответствии со спектральной моделью Хилла–Эндрюса [12]:

г

Ф n ( k x ,k y ) - 0,033 C 2 1 + 1,802,

I

k x ² +k y ² k l ²

- 0,254

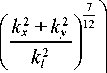
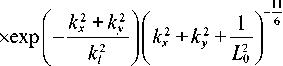
где kx , ky = –π/Δ, …, π/Δ, kl = 3,3/ l 0 ; l 0 = 1 мм и L 0 =50 м – внутренний и внешний масштаб турбулентности соответственно, Cn ² = 10^–12 м^–2/3 – индекс атмосферной рефракции. Фазовый спектр Ф ( k_x , ky ) связан со спектральной плотностью флуктуаций индекса рефракции Ф n ( kx , ky ) выражением [7, 9]:

Ф(kx,ky) - 2пk02z0Фn (kx,ky), где z0 =300 м – расстояние между излучателем и приемником, k0 =2π / λ – волновое число, λ = 1550 нм – длина волны лазерного излучения. Различные реализации фазовых экранов строятся с помощью обратного быстрого преобразования Фурье (БПФ) F-1 :

При вычислении прямого преобразования Фурье исходное двумерное распределение (во вложенных фигурных скобках) размером M × M точек дополняется нулями до N × N = 1024×1024. В результате приемная матрица фотодетектор (размером K × K = 128×128 точек) фиксирует центральную часть изображения (3) с добавлением нормального шума с нулевым средним и дисперсией σ = 10^–2.

При моделировании используется трехслойная полносвязная нейронная сеть. Входными данными для сети является распределение интенсивности I ( x , y ), искаженное турбулентной атмосферой. Первый слой содержит 1000 нейронов с функцией активации leaky ReLU. Второй слой с той же функцией активации является «бутылочным горлышком», и его размер P определяет количество параметров, используемых при построении компенсирующего транспаранта третьим слоем сети. Значения с выходов последнего слоя ( M × M = 4096 нейронов с функцией активации гиперболический тангенс), умноженные на π, представляются в виде квадратной матрицы, которая является корректирующей фазовой маской ф ( x,y ) .

Тогда после коррекции распределение интенсивности на приемнике принимает вид:

I ( ^x,y ) ^-

U ( k_x , k_y ) T ^ { e ^x,y ) G ( x,y,w₀ ) e ^x,y ) e^{i 6( x,y} ) } }

2 (4)

ˆ

Ф( х,У ) - ^4 F M A L

{ С ^ Ф ( k x ,k y ) }

здесь C – набор (размером M × M ) независимых случайных комплексных величин, распределенных нормально с нулевым средним и единичной дисперсией, знак R указывает на то, что используется только действительная часть от получившегося распределения в квадратных скобках.

Отсюда видно, что в случае ф ( x,y ) - -ф ( x,y ) получим неискаженное изображение на приемнике:

I 0 ( x,y ) ^-I ( x,y ) I ф ( xy ) - 0 .

В процессе обучения минимизируется среднеквадратичное отклонение (СКО) между неискаженным изображением и тем, которое получается в результате коррекции:

E^- 7? E| I 0 ⁽ x,y ) - I ⁽ x,y )| 2 .

K x',y'

Существенным для некоторых приложений является необходимость сохранения топологического заряда пучка [13, 14]. Однако несложно показать, что так как распределение интенсивности однозначно зависит от l, то минимизация E приводит к восстанов-

лению исходного заряда [15]. Поскольку СКО E имеет аналитическую зависимость от выходных значений сети, обучение осуществляется методом обратного распространения ошибки. Для эффективного расчета градиентов ошибки от настраиваемых параметров сети граф вычислений строится с помощью библиотеки Tensorflow 1.14. Минимизация E осуществляется за 300 итераций адаптивного алгоритма Adam. На каж- а)

б)

Рис. 2. Распределения интенсивности на фотоприемнике без искажений (а), до (б) и после коррекции (в) для топологического заряда l = 5 при P = 30

дой итерации ошибка вычисляется на обучающем множестве, которое содержит 2000 пар изображений I 0 ( x , y ) и I ( x , y ) с различными значениями орбитального момента l = 1,…, 10.

На рис. 2 и 3 изображены распределения интенсивности без искажений ( а , б ) и после коррекции ( в ) для двух значений топологического заряда l =5 (рис. 2) и l =3 (рис. 3) при P =30.

в)

б)

Рис. 3. Распределения интенсивности без искажений (а), до (б) и после коррекции (в) для топологического заряда l = 3 при P = 30

В этом случае после коррекции СКО в среднем уменьшается приблизительно в 1,8 раза вне зависимости от значения топологического заряда l. На рис. 4 приведена зависимость <  E > усредненного СКО E по 50 различным реализациям от числа параметров P . Из графика видно, что оптимальное число параметров P =30 и дальнейшее их увеличение не приводит к улучшению коррекции. Рис. 2, 3 и 4 построены для реализаций турбулентности не используемых при обучении нейронных сетей.

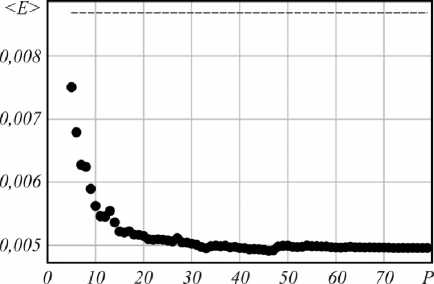
Рис. 4. Зависимость усредненного СКО от числа параметров P (показана точками). Пунктирной линией показано усреднённое СКО без компенсации

Необходимую пропускную способность служебного канала передачи данных можно оценить исходя из времени корреляции:

т = - (0,55 c n k 02 z 0 )" ⁵ v 0

между реализациями турбулентности [16]. При поперечной скорости ветра v 0 =7 м/с получаем τ ≈ 1 мс, тогда если на каждый параметр необходимо 32 бита, то необходимая общая емкость служебного канала равна 32 P / τ = 0,96 Мбит / с. В работе [10] авторам удалось добиться уменьшения СКО после коррекции в 3 раза, но при этом требуется передавать целиком изображение размером 128×128 точек, тогда, если на точку требуется 8 бит, то необходимая емкость канала при тех же условиях составляет 131 Мбит / с.

Заключение

После предварительного обучения сети на модельных распределениях ее веса можно подкорректировать с использованием данных, полученных экспериментально. Для этого можно воспользоваться процедурой, описанной в работе [17]. В этом случае также используется метод обратного распространения ошибки, но градиент ошибки вычисляется не аналитически, а с помощью имитатора среды. Использование нейронной сети позволяет не только эффективно решать обратную задачу по вычислению компенсирующего транспаранта, но и описать этот транспа- рант малым количеством параметров. На наш взгляд, представляется возможным улучшить эту схему применением более глубоких нейронных сетей, с помощью которых достигнута высокая точность распознавания изображений.

Исследование выполнено за счет гранта Российского научного фонда (проект № 18-79-00080).