Метод коррекции конечно-элементных моделей динамических систем
Автор: Красноруцкий Д.А., Лакиза П.А., Бернс В.А., Жуков Е.П.
Статья в выпуске: 3, 2021 года.
Бесплатный доступ
Предлагается метод коррекции конечно-элементных (КЭ) моделей динамических систем по результатам модальных испытаний. Целью коррекции является изменение спектра частот собственных колебаний. Метод заключается в изменении матрицы жесткости посредством добавления корректирующей КЭ-модели, построенной на узлах исходной модели в соответствии с существующими взаимосвязями между линейными степенями свободы. В качестве параметров коррекции, подлежащих определению, выступают жесткости элементов корректирующей модели. Целевой функцией является взвешенная сумма квадратов разностей между целевыми (найденными экспериментально) и текущими обобщенными жесткостями. Выполняется итерационный процесс, на каждом шаге которого осуществляется безусловная минимизация целевой функции методом сопряженных градиентов. Для расчета текущих обобщенных жесткостей используются собственные векторы, найденные из решения обобщенной проблемы собственных значений на предыдущем шаге. Метод не имеет ограничений по числу степеней свободы КЭ-моделей и не нарушает симметрию матриц. Он позволяет выделять отдельные участки конструкции, подлежащие коррекции, проводить поэтапную коррекцию, в ходе которой в качестве целевых принимаются различные группы частот. Кроме того, могут быть учтены геометрические особенности конструкции, например наличие плоскостей симметрии и конструктивно идентичных элементов. Метод реализован в виде программы и протестирован на примере свободной динамически подобной модели самолета Ту-204 (ДПМ). Для проведения экспериментального модального анализа ДПМ была вывешена на упругой подвеске малой жесткости. Проведена коррекция КЭ-модели ДПМ из объемных элементов по шести наборам экспериментально определенных частот собственных колебаний. Целевые частоты при коррекции по каждому из шести наборов были достигнуты с высокой степенью точности.
Конечно-элементная модель, собственные колебания, обобщенные модальные характеристики, коррекция матрицы жесткости, mac-критерий, модальный анализ, корректирующие жесткости, ферменные конечные элементы, объемные конечные элементы, динамически подобная модель самолета
Короткий адрес: https://sciup.org/146282371
IDR: 146282371 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.3.08
Текст научной статьи Метод коррекции конечно-элементных моделей динамических систем
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2021PNRPU MECHANICS BULLETIN
Конечно-элементные модели (КЭ-модели) широко используются для проведения статистических и динамических расчетов во многих областях техники. Однако такие модели в ряде случаев содержат неизбежные погрешности моделирования, обусловленные дискретизацией модели, неточностью задания свойств материалов, геометрических характеристик и граничных условий [1]. Для устранения погрешностей моделирования были разработаны различные методы коррекции КЭ-моделей применительно к разным конструкциям: топливным бакам ракет-носителей [2], соплу ракетного двигателя [3], композитному самолету [4], архитектурным сооружениям [5], пластинчатым теплообменникам [6]. В основе этих методов лежит минимизация разницы между ключевыми характеристиками реальной конструкции и параметрами КЭ-модели. В качестве таких параметров могут выступать, например, частоты собственных колебаний и отклик конструкции на динамическое воздействие [7]. Кроме того, методы коррекции нередко используются для оценки поврежденностей различных конструкций: дамб [8], мостов [9, 10], контейнеров для хранения радиоактивных отходов [11]. Обзор подходов к решению проблемы мониторинга поврежденности приведен в работе [12].
Следует отметить, что погрешность описания механических свойств реальной конструкции методом конечных элементов зачастую обусловлена особенностя- ми моделирования узлов сопряжения, например болтовых и заклепочных соединений. Однако описание нелинейного поведения таких узлов посредством построения нелинейной КЭ-модели в ряде случаев может оказаться вычислительно затратным. Во избежание этого такие узлы сопряжения могут быть заменены специальными элементами с эквивалентными жестко-стными и диссипативными характеристиками. Так, в работах [13, 14] болтовые узлы сопряжения двухбалочной модели были заменены гистерезисными элементами Iwan’a, параметры которых были определены методом коррекции.
Известные методы коррекции могут быть разделены на две категории: стохастические и детерминированные. В основе стохастических методов лежит представление о том, что экспериментальные данные являются случайными и содержат неизбежные ошибки измерения, обусловленные как объективными факторами (температура, влажность, вибрации, оборудование), так и субъективными (опыт проведения экспериментов) [15]. В зависимости от типов ошибок измерения были разработаны различные методы коррекции: метод симуляции Монте-Карло [16, 17], методы пертурбаций [18, 19], методы случайных поверхностей отклика [20, 21] и Байесовcкие методы [22, 23]. Однако стохастические методы коррекции на несколько порядков вычислительно затратнее детерминированных методов. Заметим, что вопрос выбора параметров коррекции для стохастических методов не является однозначным [24].
Детерминированные методы коррекции обычно сводятся к итерационной процедуре коррекции параметров КЭ-модели. Среди итерационных методов наиболее популярным и интуитивно понятным является подход, основанный на создании матрицы чувствительности [25–28]. В основе этого метода лежит проблема минимизации целевой функции, равной сумме квадратов разностей между измеренными в эксперименте данными и соответствующими данными, полученными с помощью модели. Удобство такого подхода заключается в том, что в целевой функции одновременно могут фигурировать разнородные параметры, такие как собственные частоты и отклики конструкций на динамическое воздействие. Чтобы уравновесить вклад этих данных в результирующую функцию, авторы работы [29] вводят весовые коэффициенты, значения которых определяют методом анализа иерархий.
Нередко применение методов коррекции приводит к тому, что результирующая система уравнений является плохо обусловленной [30]. Для борьбы с этой проблемой существуют две техники регуляризации, наиболее часто используемые исследователями: регуляризация Тихонова [31, 32] и сингулярное разложение [33]. Особенности применения обоих подходов на примере модели бетонного сооружения показаны в работе [34].
В данной работе предлагается детерминированный метод коррекции КЭ-моделей конструкций по результатам модальных испытаний. Матрица масс считается определенной точно и в ходе коррекции не изменяется.
1. Метод коррекции конечно-элементной модели
Пусть задана конечно-элементная модель исследуемого объекта в виде матрицы жесткости K и матрицы масс M , тогда собственные числа X = ( 2 nv ) 2 (где v -частота собственных колебаний) и формы колебаний Y определяются из решения обобщённой проблемы собственных значений:
( K -X M ) Y = 0 . (1)
Для коррекции динамических свойств КЭ-модели будем вносить изменения только в матрицу жесткости путем добавления к исходной матрице K матрицы жесткости корректирующей КЭ-модели A K . Для модели из объемных элементов предлагается использовать в качестве корректирующей КЭ-модели невесомую ферменную конструкцию, которая строится на узлах исходной КЭ-модели. Заметим, что жесткость корректирующих элементов может быть отрицательной для изменения упругости конструкции в сторону уменьшения. Жесткость каждого такого «ферменного» элемента является параметром коррекции, подлежащим определению из решения задачи безусловной минимизации целевой функции.
На рис. 1 приведена принципиальная схема, иллюстрирующая физическую сторону предлагаемого метода на примере четырехузлового КЭ в виде пространственного тетраэдра. В данном случае добавлено 6 ферменных элементов (по сути, это 6 пружин) для коррекции упругости суммарной модели. Таким образом, корректирующая модель образует «каркасную» структуру, которая подходит для коррекции моделей из объемных КЭ-элементов. В случае, когда корректируемые динамические свойства модели существенно зависят от из-гибных и крутильных жесткостей её балочных или оболочечных элементов, необходимо вводить корректирующую модель из балочных элементов. Рассмотрение этого случая выходит за рамки данной статьи.
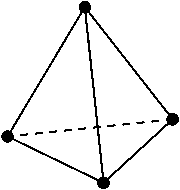
Рис. 1. Создание корректирующей КЭ-модели на примере четырехузлового КЭ в виде пространственного тетраэдра
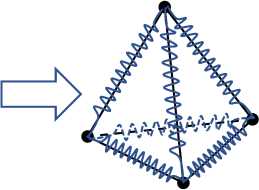
Fig. 1. Creating the updating finite element model illustrated by the example of a tetrahedrical finite element
Матрица жесткости корректирующего элемента строится как ферменный конечный элемент и имеет следующий вид:
где ,, – направляющие косинусы; с – неизвестная корректирующая жесткость; m – число корректирующих элементов. Матрица (2) симметричная, поэтому не нарушает симметрию матрицы жесткости корректируемой модели при суммировании с ней.
Для автоматического формирования набора корректирующих элементов используется портрет матрицы жесткости корректируемой конструкции. Так, если в матрице линейные степени свободы двух узлов «связаны» между собой внедиагональными элементами, то добавляется корректирующий элемент между этими узлами. В общем случае число корректирующих элементов определяется количеством связей между узлами в матрице, но оно может быть уменьшено посредством выбора областей коррекции, например элементов кон- струкции с наибольшей неопределенностью физических и геометрических характеристик. Кроме того, число независимых корректирующих жесткостей может быть уменьшено посредством введения зависимостей между элементами. Например, могут быть учтены геометрические особенности конструкции: наличие плоскостей симметрии и конструктивно идентичных элементов. Также можно проводить поэтапную коррекцию, в ходе которой в качестве целевых принимаются различные группы частот.
В зависимости от геометрии модели и типов конечных элементов может получиться так, что при добавлении (2) к матрице жесткости исходной конструкции появятся новые ненулевые элементы (изменится портрет разреженной матрицы). Такая ситуация возникает, например, когда есть геометрическая симметрия относительно некоторого узла и в исходном портрете соответствующие элементы при ассемблировании матрицы жесткости в сумме дают ноль и не попадают в портрет. Поэтому перед началом процедуры коррекции портрет матрицы жесткости дополняется портретом корректирующей матрицы.
Рассмотрим алгоритм метода коррекции на примере одного целевого значения для упрощения индексных обозначений, а затем обобщим формулы для случая коррекции по нескольким значениям собственных частот. Пусть в результате коррекции необходимо достигнуть целевого значения X . Необходимо найти такую A K * , чтобы достигнуть значения X при решении следующей обобщенной проблемы:
[ ( K + A K * ) -X * m ] Y * = 0 . (3)
Так как в (3) собственный вектор Y * зависит от матрицы A K * , то использовать (3) напрямую как нелинейное матричное уравнение для поиска корректирующих жесткостей слишком затратно с вычислительной точки зрения: придется многократно решать обобщенную проблему. Поэтому для поиска корректирующей матрицы A K * предлагается следующий итерационный алгоритм.
Пусть решена обобщенная проблема для исходной модели
( к -X( 0 ) M ) Y ( 0 ) = 0, (4)
то есть найдены X( 0 ) и Y ( 0 ) . Здесь и далее верхний индекс в круглых скобках обозначает номер итерации. На первой итерации ищем такое A K ( 1 ) , чтобы удовлетворить следующему уравнению:
-
[ ( k + A K ( 1 ) ) -X * m ] Y ( 0 ) = 0 . (5)
Здесь необходимо отметить, что A K ( 1 ) является функцией от корректирующих жесткостей c , c ... c .
Число корректирующих элементов m в общем случае больше размерности матрицы жесткости N , а следовательно, больше числа уравнений в (5). Поэтому для решения (5) необходимо устремить к нулю следующую скалярную величину (невязку):
-
f ( 1 ) = Y ( 0 ) T [A K ( 1 ) - AX( 1 ) * M ] Y ( 0 ), (6)
где AX( 1 ) = X * - X( 0 ) .
В результате минимизации невязки (6) по корректирующим жесткостям получим A K ( 1 ) и, решив новую обобщённую проблему
-
[ ( K + A K ( 1 ) ) - X( 1 ) M ] Y ( 1 ) = 0, (7)
найдем X( 1 ) и Y ( 1 ) . Это первая итерация метода. Аналогично (5) составим следующее уравнение для поиска A K ( 2 ) :
[ ( k + A K ( 1 )+A K ( 2 ) ) -X * M ] Y ( 1 )= 0, (8)
представим X* = (x(1) + AX(2)*), тогда (8) перепишется в следующем виде:
(K + AK(1) + AK(2)) - (X(1) + AX(2)*) M [aK(2)-AX(2)*M ] Y(1) = 0, где AX(2) = X -XU). Аналогично (6) устремим к нулю невязку
-
f ( 2 ) = y ( 1 ) T [a k ( 2 ) - aX( 2 ) * m ] Y ( 1 ). (10)
Y (1) = 0;
Это была вторая итерация метода коррекции. Обобщим формулы на случай нескольких целевых собственных значений. Пусть их число равно s . Таким образом, на каждой итерации метода коррекции минимизируется следующая целевая функция:
s
F C1, C2^. ) = E w[ f j+1)] = i=1
s
= £ w ( Y ( j ) T A K ( j +1 ) Y ( j ) - AX( j +1)* Y ( j ) T M Y ( j ) ) ^ min, (11) i = 1
где j – номер итерации; w – весовой коэффициент i -го тона.
Для минимизации (11) используется метод сопряженных градиентов. С вычислительной точки зрения важно найти аналитические выражения для вектора-градиента целевой функции. Для этого найдем производные от целевой функции по неизвестным корректирующим жесткостям (здесь и далее опустим номер итерации в круглых скобках):
d F г 5 f ,
— = 2 E wf^ , P = 1" m .
d C P -= 1 d c p
Пусть y(r), i = 1..N - компоненты вектора собственной формы Y , тогда частные производные -f- из (12) r д Ср примут вид
f- = А( Y д к Y. ) = £ у Г'£ уи , r = 1.. , ,
З ср д Ср j = 1 - = 1 дСр
р = 1.. m .
Для вычисления (13) нет необходимости «прокручивать» два цикла (суммы), так как ненулевыми компо-дДк нентами ---- в общем случае без учета симметрии дСр
являются максимум 36 элементов в (2), поэтому (13) можно заменить на циклы по элементам (2). Рассмот-
рим такую замену на примере одного корректирующего элемента. Для удобства изложения обозначим произведения направляющих косинусов как Pz? и введем ло-
кальную нумерацию элементов, входящих в произведения (13):
У 1
У 2
У з
< —f
У 4
У 5 . У 6
<
T
р11
Р 12 - Р -з.. -0 11 -0 12
<-Р 13
Р 12 Р 13
в 22 P 23
в 23 Р з3
-Р11
-Р12
-Р13
-Р 12 -Р 13 ; "вГТ/
—в 22 -Р 23 ; Р12 Р 22
-Р 23 -в 33 : Р 13 Р 23
-Р13 )
Р 23
-Р 33
Р 13
Р 23
Р 33 V
У 1
У 2 .у3.., У 4 У 5 . У 6
= 0 11 ( У 1 - У 4 ) 2
+
+ Р 22 ( У 2 - У 5 ) 2 + 0 33 ( У 3 - У 6 ) 2 + 2 в 12 ( У 1 У 2 - У 1 У 5 - У 2 У 4 + У 4 У 5 ) +
+ 2₽ 13 ( У 1 У 3 - У У б - У 3 У 4 + У 4 У б ) +
+ 2Р 23 ( У 2 У 3 - У 2 У б - У 3 У 5 + У 5 У б ) . (14)
На основе выражений (14) можно вычислить производные f . Рассмотрим другой вариант вычисления д Ср производных. Для этого воспользуемся тем фактом, что
симметричные матрицы хранятся в виде верхнего или нижнего треугольника, причем в разреженном формате хранения матрицы её элементы отсортированы в порядке возрастания номеров строк и столбцов. Для определенности рассмотрим построчное хранение разреженной матрицы:
ГР 1 в 2
₽ 7
Д К = c j
Р3 iP4 р5 Рб
Р8 ! Р9 Р10
Р12 ' Р13 Р14
Р 18
Р 20
Р 21 у
В (15) введена другая нумерация произведений направляющих косинусов, и для удобства отрицательный знак внесен в значения соответствующих элементов. В общем виде один корректирующий конечный элемент
с учетом симметрии имеет максимально 21 ненулевой элемент. В зависимости от конкретных значений направляющих косинусов ненулевых элементов в (15) может быть меньше. Для каждого корректирующего элемента предлагается хранить все произведения направляющих косинусов в виде последовательности в,Р2..Дцур где L ( j ) - количество ненулевых элементов j -го корректирующего конечного элемента. Кроме того, для каждого такого элемента хранится порядковый номер элемента в портрете разреженной матрицы жесткости, по которому можно определить строку - , столбец j (от 1 до N ) и соответствующие номера степеней свободы id , jd (принимают значения от 1 до 3, соответствуют перемещениям вдоль осей глобальной системы координат). Тогда формула для вычисления производной (13) примет вид
I f- = Е р k [-5 -d,jd ( У - - У ) 2 + ( 1 - 5 -d , jd ) 2 У - У ] ,(16)
где 5. j - символ Кронекера.
Если сравнить вычислительные затраты на (14) и (16), первый имеет примерно в 2 раза меньше умножений, но для его реализации требуется дополнительная память на массив, содержащий Pt р Р22, Р33, Рг2, Pt3, Р23 для каждого корректирующего элемента.
В процессе итераций при «движении» к целевым значениям частот возможно изменение порядка частот, особенно при наличии в спектре близких и кратных частот, поэтому после каждой итерации необходимо находить соответствие новых тонов колебаний старым. Обычно это можно сделать, используя критерий модального соответствия (MAC-критерий):
( ~ \ ( Y T Y ) 2
MAC( Y , Y) = ,? _х/—г,
( , ) ( Y T Y )( Y T Y )
однако при наличии кратных частот колебаний MAC-критерий может дать близкие численные значения сразу для нескольких форм колебаний, что не позволяет установить однозначное соответствие между формами колебаний до и после коррекции. Для решения этой проблемы предлагается находить собственные частоты и формы колебаний на каждом шаге коррекции методом итераций в подпространстве [35], используя в качестве начальных приближений векторы, найденные на предыдущем шаге.
Рассмотрим более общий алгоритм, который в частном случае вырождается в представленный выше. Представим X =Х( 0 )+ДХ , тогда (5) перепишется в следующем виде:
[ ( к + д к ( 1 ) ) - ( х( 0 )+ДХ * ) M ] Y ( 0 ) = 0 . (17)
Вычтем (4) из (17), составим целевую функцию для поиска Д К ( 1 ) :
{ Y T [a k ( 1 ) -AX * m ] Y } ^ min, где AX * = X * -X ( o ) . (18)
Решив задачу минимизации (18), получим A K ( 1 ) и решим новую обобщенную проблему:
[ ( k + A K ( 1 ) ) -X ( 1 ) m ] Y ( 1 ) = 0. (19)
При этом X( 1 ) ^ X * , если A K ( 1 ) ^ A K * и Y ( 1 ) # Y * .
Сформируем целевую функцию для поиска второго приближения A K ( 2 ) . Невязка будет иметь следующий вид:
f = [ ( К + A K ( 2 ) ) - ( x ( 0 ) + АХ * ) M ] Y ( 1 ) ;
f = [ ( К + a k ( 2 ) ) - ( x :" + AX * ) M ] ( y ( 0 ) + a y ( 1 ) ) .
Умножим f слева на транспонированный собственный вектор, получим
{y(0) T [ak(2)-ax*m] y(0) +
+ Y ( o ) T [ ( k + A K ( 2 ) ) -X * m ]a Y ( 1 ) | 2 ^ min. (20)
Решив задачу минимизации (20), будем иметь А К ( 2 ) . Решим новую обобщенную проблему:
[(k+ak(2))-x(2)m] y(2) = 0 .
При этом X( 2 ) # X , если А К ( 2 ) ^ А К и Y ( 2 ) ^ Y . Сформируем целевую функцию для поиска третьего приближения A K ( 3 ) :
{[ ( k + a k ( 3 ) ) - ( x + ax * ) m ] ( y ( 0 ) + a y ( 2 ) ) } 2 ^ min.
В итоге аналогично (20) получим
{y(0) T [ak(3) —ax*m] y(0) +
+ Y(o)T [(k + AK(3))-X*M]AY(2)|2 ^ min. (21)
Таким образом, проанализировав (20) и (21), для поиска корректирующей матрицы жесткости a k ( i + 1 ) ^a k * имеем следующую целевую функцию:
{ Y (o) t [A K ( i + 1) -AX * m ] Y (o) +
+ Y (o) t А К ( i + 1)A Y ( i ) + Y (o) t [ К - X * m ] A Y ( i ) } 2 ^ min. (22)
Выберем следующую нормировку для собственных v ( 0 )
векторов Y :
y (0) t my (0) = 1.
После решения обобщенной проблемы нормируем Y ( i ) - сначала Y ( i ) T M Y ( i ) = 1 , для установления соответствия тонов колебаний до и после коррекции по МАС-критерию, а затем Y (o) t M Y ( i ) = 1, тогда
y ( 0 ) t m ( y ( 0 ) +a y ( i ) ) = 1 , y (0) t m a y ( i ) = 0 .
Таким образом, целевая функция (22) примет следующий вид:
{ y ( 0 ) T A K ( i + 1) Y ( i ) + ( Y ( o ) T К A Y ( i ) - ax * ) } 2 ^ min . (23)
Выражения для производных от целевой функции, входящие в градиент по типу (16), имеют следующий вид:
L ( p )
= Z ₽ k [-S id ,jd ( y - y j ) ( a y i -A y j ) +
° c p k = 1
+ ( 1 -s M , jd )( у Д y j + yj А y ) ] , (24)
где у - компоненты вектора Y ( o ) , а А у - компоненты вектора A Y (1) .
Таким образом, в целевой функции (23) содержатся собственные векторы для двух обобщенных проблем: исходная [ К - X (o) M ] Y (o) = 0 и достигнутая в процессе итераций проблема для скорректированной матрицы [( К + А К ( ‘) ) — X( i ) M ] Y ( i ) = 0 для поиска следующего приближения корректирующей матрицы А К ( i + 1 ) . Если обновлять «базовую точку» итерационного процесса на каждой итерации, то получим первый алгоритм с целевой функцией (10) при условии выбора нормировки собственных форм к единичным обобщенным массам: ( Y ( i ) T А К ( i + 1) Y ( i ) -AX( i + 1) * )2 ^ min.
Сходимость представленного итерационного алгоритма существенно зависит от геометрии и физического соответствия расчетной модели реальной конструкции, поэтому она определяется практическим путем в каждом конкретном случае на основе требований, предъявляемых к расчетной модели летательного аппарата. Так, например, если назначением модели является оценка эксплуатационной нагруженности летательного аппарата, то, как правило, коррекция расчетной модели призвана обеспечивать соответствие с заданной точностью расчетных значений собственных частот низших тонов колебаний их экспериментальным значениям. В то же время решение проблемы аэроупругой устойчивости самолетов требует сохранения в расчетной модели собственных частот таких тонов, которые оказывают первостепенное влияние на исследуемое явление. И степень соответствия модели реальной конструкции здесь определяется ограничениями максимальной скорости летательного аппарата.
-
2. Апробация метода
Алгоритм предложенного метода коррекции реализован в виде программы на языке Fortran. Программа была успешно протестирована на простых КЭ-моделях, составленных из оболочечных и объемных элементов.
Для апробации метода на примере реальной конструкции была выбрана динамически подобная модель самолета Ту-204 (ДПМ), выполненная по отсечнобалочной схеме (рис. 2). Габаритные размеры: размах крыла 3172 мм, длина фюзеляжа 3462 мм (масштаб моделирования 1:10). Масса с датчиками и кабелями 50,5 кг. Упругие характеристики фюзеляжа и крыла смоделированы лонжеронами, расположенными по оси жёсткости каждого агрегата. Топливо, коммерческая нагрузка, оборудование, носовая и основные опоры имитировались жёсткими сосредоточенными грузами. Для проведения экспериментального модального анализа ДПМ была вывешена на упругой подвеске малой жесткости.

Рис. 2. Общий вид ДПМ на упругой подвеске
Fig. 2. General view of the dynamically-scaled model with the flexible suspension
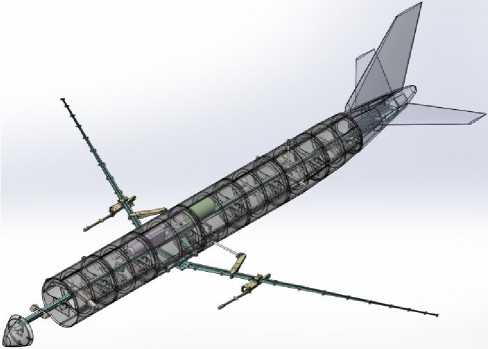
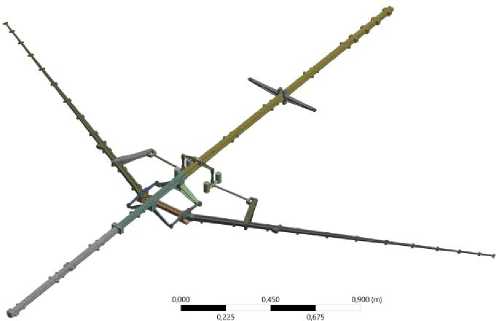
Создание 3D-модели (рис. 3, a ) производилось по натурной ДПМ. Геометрические модели крыльевых отсеков не создавались, так как они, в силу конструктивного исполнения ДПМ, являются точечными массами для упругого крыла – они не вносят жесткостей и не соприкасаются между собой при малых амплитудах колебаний. В силу последнего обстоятельства отсеки и хвостовое оперение при создании КЭ-модели также моделировались дискретными массами с инерционными характеристиками, определенными по соответствующим геометрическим моделям. Число степеней свободы в результирующей КЭ-модели (рис. 3, б ) составило 751871.
Коррекция КЭ-модели проводилась по шести наборам экспериментально определенных частот:
-
1) по 7 тону – симметричный изгиб крыла I тона (СИКр1);
-
2) с 7 по 8 тон – СИКр1, антисимметричный изгиб крыла I тона (АСИКр1);
-
3) с 7 по 9 тон – СИКр1, АСИКр1, горизонтальный изгиб фюзеляжа I тона (ГИФ1);
-
4) с 7 по 10 тон – СИКр1, АСИКр1, ГИФ1, вертикальный изгиб фюзеляжа I тона (ВИФ1);
-
5) с 7 по 10 и 12 тону – СИКр1, АСИКр1, ГИФ1, ВИФ1, симметричный изгиб крыла II тона (СИКр2);
-
6) с 7 по 10, 12 и 15 тонам – СИКр1, АСИКр1, ГИФ1, ВИФ1, СИКр2, вертикальный изгиб фюзеляжа II тона (ВИФ2).
а
б
Рис. 3. Геометрическая ( a ) и конечно-элементная ( б ) модели ДПМ
Fig. 3. Geometrical ( a ) and finite element ( b ) models of the dynamically-scaled model
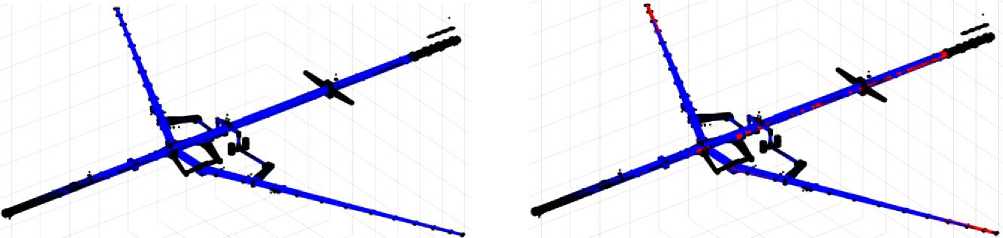
Итерационный процесс коррекции по предложенному алгоритму считался завершенным при достижении целевых значений частот с точностью 0,0001 %. Результаты коррекции сведены в таблице. Распределения изменений узловых жестокостей по всем линейным степеням свободы КЭ-модели до и после каждой из коррекций приведены на рис. 4, a–е . Синяя цветовая гамма на рисунках соответствует областям понижения исходной жесткости (корректирующая КЭ-модель имеет отрицательную жесткость в этих областях), а красная – областям повышения исходной жесткости. Черному цвету соответствуют области, жесткость которых в ходе коррекции осталась неизменной.
Заметим, что коррекция по одному тону (набор 1) приводит к снижению жесткости практически во всех областях (рис. 4, a) с измененной жесткостью. Добавление в набор других тонов приводит к появлению облас- тей с положительным изменением жесткости в узлах (рис. 4, б–е). При этом для каждого набора распределение корректирующих жесткостей уникально.
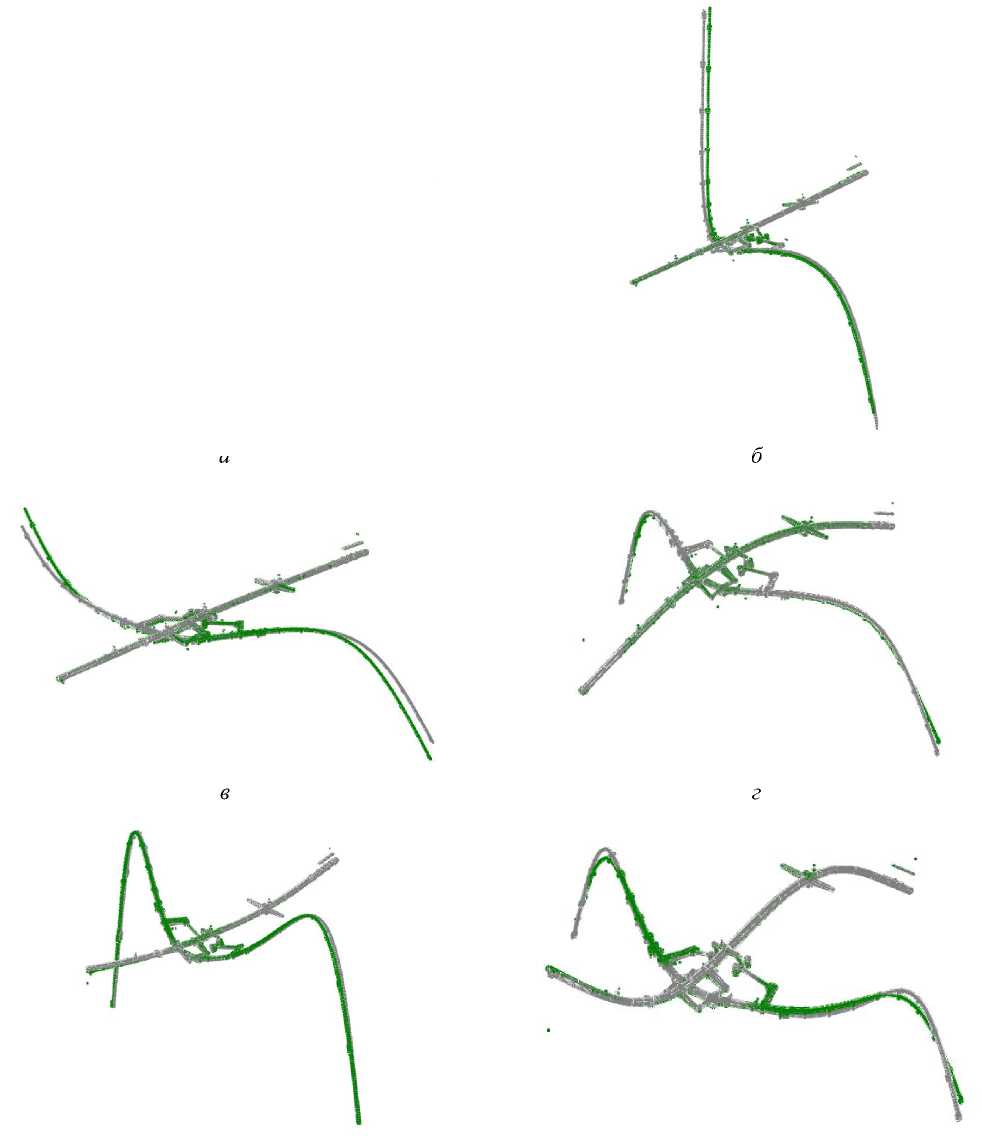
Вследствие изменения упругости корректируемой модели происходит изменение частот и форм колебаний. Нормированные к массе формы колебаний до (серым цветом) и после коррекции (зеленым цветом) по шестому набору частот приведены на рис. 5. Из рисунков видно, что формы колебаний до и после коррекции хорошо коррелируют между собой, разница между формами колебаний по MAC-критерию до и после коррекции составила: 0,02, 1,12, 1,74, 0,87, 0,18 и 4,09 % соответственно.
Результаты коррекции
Results of the model updating
|
Тон |
Частота, Гц |
Погрешность до и после коррекции, % |
|||||||
|
эксперимент |
исходная модель |
до |
после |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||||
|
СИКр1 |
3.440 |
3.492 |
1.5 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|
АСИКр1 |
4.873 |
4.955 |
1.7 |
-0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|
ГИФ1 |
5.440 |
5.728 |
5.3 |
4.7 |
4.7 |
0.0 |
0.0 |
0.0 |
0.0 |
|
ВИФ1 |
5.730 |
5.968 |
4.2 |
3.5 |
3.3 |
2.6 |
0.0 |
0.0 |
0.0 |
|
СИКр2 |
9.300 |
9.131 |
-1.8 |
-4.4 |
-3.2 |
-3.9 |
-4.4 |
0.0 |
0.0 |
|
ВИФ2 |
14.18 |
14.77 |
4.2 |
3.7 |
3.8 |
3.4 |
2.0 |
3.3 |
0.0 |
a б
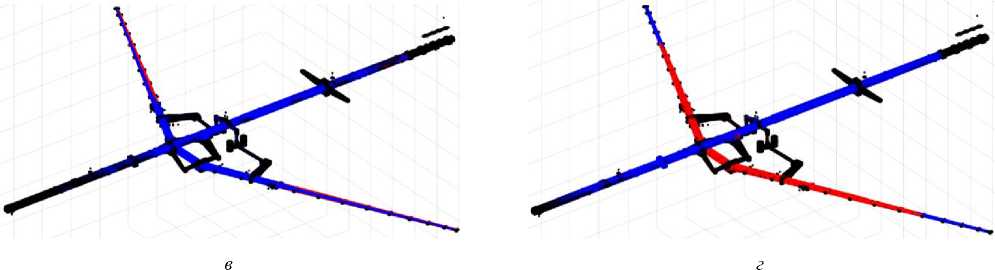

Рис. 4. Распределения изменений узловых жесткостей при коррекции: по наборам целевых частот от 1 до 6 ( a–е )
Fig. 4. Alterations of nodal stiffnesses during updating: by the sets of the target frequencies from 1 to 6 ( a-f )
д
е
Рис. 5. Формы колебаний до и после коррекции: a – СИКр1; б – АСИКр1; в – ГИФ1; г – ВИФ1; д – СИКр2; е – ВИФ2
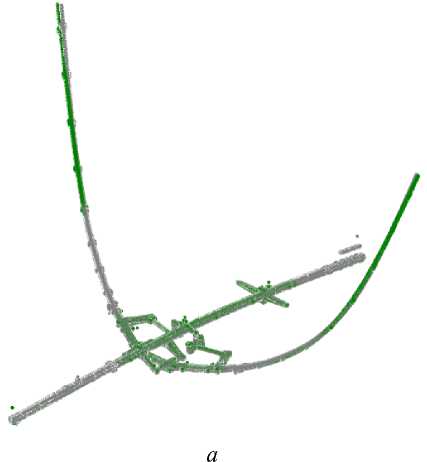
Fig. 5. Modeshapes before and after updating: a – the first symmetric wing bending; b – the first asymmetric wing bending; c – the first horizontal fuselage bending; d – the first vertical fuselage bending; e – the second symmetric wing bending; f – the second vertical fuselage bending
Заключение
Предложен метод коррекции расчетных динамических моделей, который состоит в том, что к исходной матрице жесткости добавляется матрица жесткости корректирующей КЭ-модели, при этом матрица масс считается определенной точно и не изменяется в ходе коррекции. В рамках данной работы корректирующая модель представляет собой невесомую ферму, построенную на узлах исходной модели. Жесткости корректирующих элементов вычисляются итерационно из решения задачи минимизации целевой функции, кото- рая является взвешенной суммой квадратов разности текущих и целевых значений частот собственных колебаний. Проведена коррекция свободной КЭ-модели ДПМ самолета Ту-204 по шести наборам частот собст- венных колебаний, определенных экспериментально. Целевые частоты при коррекции по каждому из шести наборов были достигнуты с высокой степенью точности.
Список литературы Метод коррекции конечно-элементных моделей динамических систем
- Bartilson D.T., Jang J., Smyth A.W. Finite element model updating using objective consistent sensitivity-based parameter clustering and Bayesian regularization // Mechanical Systems and Signal Processing. - 2019. - Vol. 114. - P. 328-345.
- Li Y., Tian K., Hao P. Finite element model updating for repeated eigenvalue structures via the reduced-order model using incomplete measured modes // Mechanical Systems and Signal Processing. - 2020. - Vol. 142.
- Finite element model updating of liquid rocket engine nozzle based on modal test results obtained from 3D SLDV technique / S. Yan, B. Li, F. Li, B. Li // Aerospace Science and Technology. - 2017. - Vol. 69. - P. 412-418.
- Zhao W., Gupta A., Regan C.D. Component data assisted finite element model updating of composite flying-wing aircraft using multi-level optimization // Aerospace Science and Technology. - 2019. - Vol. 95.
- Girardi G., Padovani C., Pellegrini D. Finite element model updating for structural applications // Journal of Computational and Applied Mathematics. - 2020. - Vol. 370.
- Modeling of plate heat exchanger based on sensitivity analysis and model updating / Y. Guo, F. Wang, M. Jia, M. Zhang // Chemical Engineering Research and Design. - 2018. - Vol. 138. - P. 418-432.
- Petersen O.W., Oiseth O. Sensitivity-based finite element model updating of a pontoon bridge // Engineering Structures. - 2017. - Vol. 150. - P. 573-584.
- Bayraktar A., Sevim B., Altunisik A.C. Finite element model updating effects on Nonlinear seismic response of arch dam-reservoir-foundation systems // Finite Elements in Analysis and Design. - 2011. - Vol. 47. - P. 85-97.
- Dinh-Cong D., Nguyen-Thoi T., Nguyen D.T. A FE model updating technique based on SAP2000-OAPI and enhanced SOS algorithm for damage assessment of full-scale structures // Applied Soft Computing Journal. - 2020. - Vol. 89.
- Polanco N.R, May G., Hernandez E.M. Finite element model updating of semi-composite bridge decks using operational acceleration measurements // Engineering Structures. - 2016. - Vol. 126. - P. 264-277.
- Experimental modal analysis and finite element model updating for structural health monitoring of reinforced concrete radioactive waste packages / J.N. Eiras, C. Payan, S. Rakotonarivo, V. Garnier // Construction and Building Materials. - 2018. - Vol. 180. - P. 531-543.
- Simoen E., Roeck G.D., Lombaert G. Dealing with uncertainty in model updating for damage assessment: A review // Mechanical Systems and Signal Processing. - 2015. - Vol. 56.
- Lacayo R.M., Allen M.S. Updating structural models containing Nonlinear Iwan joints using quasi-static modal analysis // Mechanical Systems and Signal Processing. - 2019. - Vol. 118. - P. 133-157.
- Yuan P.P., Ren W.X., Zhang J. Dynamic tests and model updating of Nonlinear beam structures with bolted joints // Mechanical Systems and Signal Processing. - 2019. - Vol. 126. - P. 193-210.
- Huang B., Chen H. A new approach for stochastic model updating using the hybrid perturbation-Garlekin method // Mechanical Systems and Signal Processing. - 2019. - Vol. 129. - P. 1-19.
- Bao N., Wang C. A Monte Carlo simulation based inverse propagation method for stochastic model updating // Mechanical Systems and Signal Processing. - 2015. - Vol. 60.
- Boulkaibet I., Mthembu L., Marwala T. Finite element model updating using the shadow hybrid Monte Carlo technique // Mechanical Systems and Signal Processing. - 2015. - Vol. 52.
- A model-updating approach based on the component mode synthesis method and perturbation analysis / T. Wang, H. He, W. Yan, G.P. Chen // Journal of Sound and Vibration. - 2018. - Vol. 433. - P. 349-365.
- Deng Z., Guo Z., Zhang X. Interval model updating using perturbation method and Radial Basis Function neural networks // Mechanical Systems and Signal Processing. - 2017. - Vol. 84. - P. 699-716.
- A stochastic model updating strategy-based improved response surface model and advanced Monte Carlo simulation / X. Zhai, C.W. Fei, Y.S.Choy, J.J. Wang // Mechanical Systems and Signal Processing. - 2017. - Vol. 82. - P. 323-338.
- Fang S.E., Zhang Q.H., Ren W.X. Parameter variability estimation using stochastic response surface model updating // Mechanical Systems and Signal Processing. - 2014. - Vol. 49. - P. 249-263.
- Xin Y., Hao H., Li J. Bayesian based nonlinear model updating using instantaneous characteristics of structural dynamic responses // Engineering Structures. - 2019. - Vol. 183. - P. 459-474.
- Lam H.F., Yang J., Au S.K. Bayesian model updating of a coupled-slab system using field test data utilizing an enhanced Markov chain Monte Carlo simulation algorithm // Engineering Structures. - 2015. - Vol. 102. - P. 144-155.
- Yuan Z., Liang P., Silva T. Parameter selection for model updating with global sensitivity analysis // Mechanical Systems and Signal Processing. - 2019. - Vol. 115. - P. 483-496.
- Mottershead J.E., Link M., Friswell M.I. The sensitivity method in finite element model updating: A tutorial // Mechanical Systems and Signal Processing. - 2011. - Vol. 25. - P. 2275-2296.
- Bakir P.G., Reynders E., Roeck G.D. Sensitivity-based finite element model updating using constrained optimization with a trust region algorithm // Journal of Sound and Vibration. - 2007. - Vol. 305. - P. 211-225.
- Sensitivity-based finite element model updating with natural frequencies and zero frequencies for damped beam structures / C.H. Min, S. Hong, S.Y. Park, D.C. Park // IJNAOE. - 2014. - Vol. 221. - P. 904-921.
- Hernandez E.M., Bernal D. Iterative finite element model updating in the time domain // Mechanical Systems and Signal Processing. - 2013. - No. 34. - P. 39-46.
- Chen L., Guo Y., Li L. Structural dynamic model updating based on multi-level weight coefficients // Applied Mathematical Modelling. - 2019. - Vol. 71. - P. 700-711.
- Hua X.G., Ni Y.Q., Ko J.M. Adaptive regularization parameter optimization in output-error based finite element model updating // Mechanical Systems and Signal Processing. - 2009. - Vol. 23. - P. 563-579.
- Li X.Y., Law S.S. Adaptive Tikhonov regularization for damage detection based on nonlinear model updating // Mechanical Systems and Signal Processing. - 2010. - Vol. 24. - P. 1646-1664.
- Density filtering regularization of finite element model updating problems / P. Reumers, C.V. Hoorickx, M. Schevenels, G. Lombaert // Mechanical Systems and Signal Processing. - 2019. - Vol. 128. - P. 282-294.
- On the application of singular value decomposition and Tikhonov regularization to ill-posed problems in hyperbolic passive location / I. Mantilla-Gaviria, M. Leonardi, J.V. Balbastre-Tejedor, E. Reyes // Mathematical and Computer Modelling. - 2013. - Vol. 57. - P. 1999-2008.
- Weber B., Paultre P., Proulx J. Consistent regularization of Nonlinear model updating for damage identification // Mechanical Systems and Signal Processing. - 2009. - Vol. 23. - P. 1965-1985.
- Bathe K., Wilson E. Solution methods for eigenvalue problems in structural mechanics // International Journal for Numerical Methods in Engineering. - 1973. - Vol. 6. - P. 213-226.


