Метод корректировки координат текущего местоположения для систем точного земледелия

Современные спутниковые навигационные системы (СНС), применяемые в большинстве устройств, имеют высокую точность позиционирования и малое время отклика. Эти особенности позволяют использовать спутниковую навигацию для точных земляных работ, таких как опрыскивание и посев, качество которых в обычных условиях не удовлетворяет предъявляемым требованиям. Однако применение СНС в точном земледелии ограничено ввиду возникновения скачков координат, причины которых различны – от тропосферных задержек из-за погодных условий до искажения сигнала, связанного с появлениями различных препятствий.

При проведении экспериментов на точность позиционирования GPS-чипа MediaTek MT3329 были получены следующие результаты: на протяжении достаточно продолжительного времени (порядка нескольких часов) позиционирование системы устойчиво, затем происходит скачок позиции на 3–4 метра и дальнейшее устойчивое позиционирование (рис. 1).

При выполнении различных точных земляных работ такие скачки координат могут внести существенную погрешность в измерении текущего положения техники и привести к значительному ухудшению качества выполняемых работ.

Предлагается математический метод коррекции, позволяющий скорректировать скачки координат GPS системы. Данный метод основан на измерении ускорения движения техники. Частота поступающих данных с СНС равна 5 Гц, следовательно, время между расчетами не превышает 200 мс. Ускорение, развиваемое техникой в этом случае, будет равно:

Е = V n - V m ) • ⁵ (м/с²), (1) где V – скорость, измеренная на прошлой итерации;

• V – скорость, измеренная на текущей итерации;

ε – ускорение, развиваемое техникой на данном интервале времени.

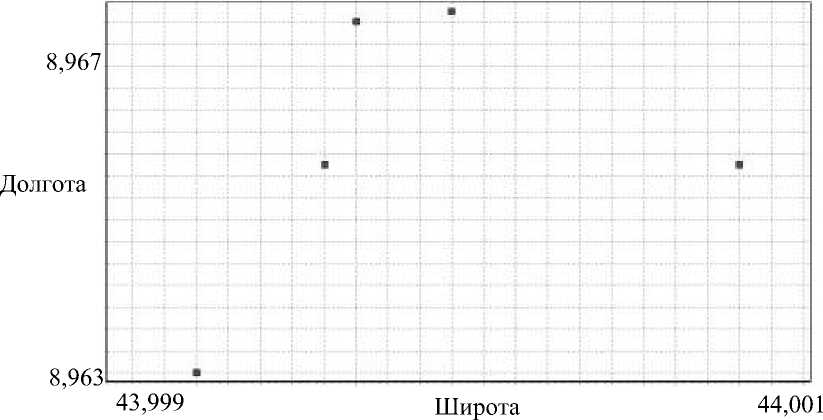
Рис. 1. Разброс значений координат при статическом позиционировании

При подстановке в формулу (1) полученных экспериментальных данных мы получим следующие значения ускорений: для первого скачка ε = 17,25 (м/с²); для второго скачка ε = 19,9 (м/с²);

не

для третьего скачка ε = 12,2 (м/с²);

для четвертого скачка ε = 2 (м/с²).

Очевидно, что при движении техника может развивать такие ускорения. На рисунке 2 представлено движение техники по криволинейной траектории.

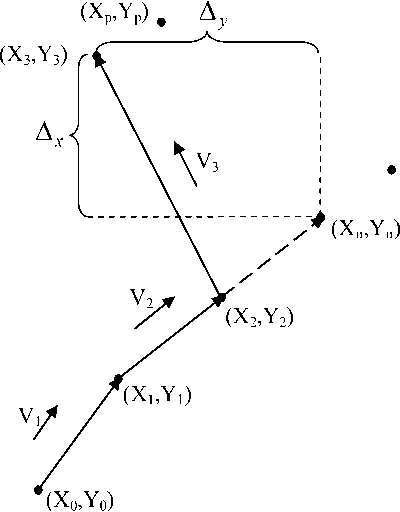
(X н ,Y н )

Рис. 2. Схема движения техники

При движении техники с СНС поступают сигналы о рассчитанном текущем местоположении (X 0 , Y 0 ), (X 1 , Y 1 ), (X 2 , Y 2 ), (X 3 , Y 3 ). В каждый момент времени позиционирования необходимо рассчитывать текущую скорость движения техники:

V i = J ⁽ x i - x o )² + ⁽ У 1 - У 0 ⁾² , (2)

V 2 = 7 ⁽ x 2 - x 1 ⁾² + ⁽ У 2 - У1⁾² , (3) V = 7 ( X 3 - X 2 ) 2 + ( У 3 — У 2 ) 2 , (4)

где V – скорость, рассчитанная в точке ( X i , У 1 );

• V – скорость, рассчитанная в точке ( X 2 , У 2 );

V – скорость, рассчитанная в точке ^{( x} 3 , У з^).

Зададим некоторое допустимое ускорение £_do . Для того чтобы обнаружить ошибку при расчете текущего местоположения (т.е. выявить факт скачка), необходимо при каждом новом поступлении координат с навигационной системы производить расчет ускорения:

S t = V m — V ,),           (5)

где £ _m - текущее рассчитанное ускорение;

V _т – текущая рассчитанная скорость;

Vп  – скорость, рассчитанная на предыдущем этапе.

При выполнении условия £_до^ S_m необходимо корректировать рассчитанное местоположение. Для этого полагаем, что движение происходило в том же направлении и с той же скоростью. Отклонения по координатам для рассматриваемого случая будут следующие:

5Х = x2 — х,(6)

5y = У2 — У1, где 5Х - отклонение по оси абсцисс;

5 у - отклонение по оси ординат.

Рассчитаем истинное положение точки:

X,. = х9 + 5,(8)

Хи = х2 + 5х.(9)

После расчета истинного положения необходимо рассчитать величину ошибки позиционирования:

АX = Хи — Х3 ,

А У = Уи— У3, где Ах - ошибка позиционирования по оси абсцисс;

А у - ошибка позиционирования по оси ординат.

Общая ошибка позиционирования будет равна сумме текущей и предыдущей ошибки:

^д х =^д пх ^+А x ,           ⁽¹²⁾

д У =д пу +А у ,           ⁽¹³⁾

где  д,x - ошибка позиционирования по оси абсцисс, рассчитанная на предыдущем этапе; при первом корректировании полагается равной нулю. дпу - ошибка позиционирования по оси ординат, рассчитанная на предыдущем этапе; при первом корректировании полагается равной нулю.

При последующих итерациях при расчете текущего местоположения при отсутствии скачка необходимо корректировать текущее местоположение:

Х н = Х р +д х ,         (14)

У н = У р +д у .          ⁽¹⁵⁾

Если же обнаружен скачок, то необходимо производить коррекцию, описанную выше.

Данный метод разработан для применения совместно со спутниковой навигационной системой GPS, реализованной на чипе MTK3329, при использовании совместно с наземной техникой. Он позволяет избежать ошибок, связанных с внезапными скачками значений координат, присылаемых с СНС. Представленный метод может быть применен с незначительными изменениями для других систем спутниковой навигации или других видов техники.