Метод математического моделирования тепловых источников в термоэлектрических элементах Пельтье

Исследования термоэлектрических свойств полупроводниковых веществ были начаты в нашей стране академиком А.Ф. Иоффе, которого теперь называют "отцом" нобелевских лауреатов [1]. Эта область физики твердого тела и по сей день является одной из наукоемких и требующих теоретических и экспериментальных разработок. Одним из промышленных воплощений термоэлектрических эффектов является термоэлектрическая батарея (ТЭБ), состоящая из полупроводниковых p—n- термопар.

В термобатарее реализуется термоэлектрический эффект Пельтье — возникновение перепада температур на ветвях термопары при подключении источника тока. Термобатареи, состоящие из термопар, в зависимости от полярности подключения могут работать как на нагрев, так и на охлаждение рабочего спая. Термобатареи, чьи характеристики оптимизированы только на эффективное охлаждение, называют термоэлектрическими микроохладителями (ТЭМО) [2-4].

Спектр применения ТЭБ в устройствах термостатирования велик. В последнее время они стали применяться в устройствах, где требуется как термостатирование с высокой точностью, так и циклический нагрев и охлаждение объекта.

Одним из таких устройств является применяемый в области технологии живых систем ампли-фикатор ДНК [5].

Подбор термобатареи для устройства термостатирования требует знания основных характеристик:

• •    номинального напряжения U (В);

• •    номинальной силы тока I (А);

• •    номинальной мощности W (Вт);

• •    холодопроизводительности Q ₀ (Вт) — при нулевой нагрузке на рабочем спае;

• •    сопротивления R (Ом).

Таким образом, для применения стандартной ТЭБ в конкретном техническом устройстве необходимо провести расчет холодо- или теплопроиз-водительности батареи при работе с тепловой нагрузкой и в условиях теплообмена.

Подобные методики расчета описаны в [2-4] и в случае стационарных условий нагрева или охлаждения дают результаты с инженерной точностью.

При аналитических расчетах рассматриваются изолированные термопарные элементы. Холодопроизводительность находится по формуле

Q x = а IТ x - -1 ² R , (1)

где T X — температура холодного спая (К); а — коэффициент термо-ЭДС; I — сила тока в цепи (А); R — сопротивление термоэлемента (Ом).

Далее используются номограммы для определения требуемого качества термопар. В случае уточнения расчета возможен учет:

• •    эффекта Томсона (эффекта возникновения дополнительной термо-ЭДС в результате градиента температур в ветви термопары);

• •    коммутационных пластин и слоев;

• •    нагрузки на спае (массы);

• •    коэффициентов теплоотдачи на спаях.

Однако применяемые расчетные формулы не эффективны по сравнению с возможностью расчета и использования численных методов и ЭВМ.

В 1991 г. ТЭБ стали применяться в качестве источника нагрева/охлаждения в устройстве, называемом амплификатором ДНК. Особенности работы амплификатора связаны с тем, что он является биотехнической системой, а следовательно, требует прецизионной точности поддержания и изменения температуры объекта нагрева/охлаждения во временных интервалах, измеряемых секундами.

Конструктивная схема амплификатора ДНК

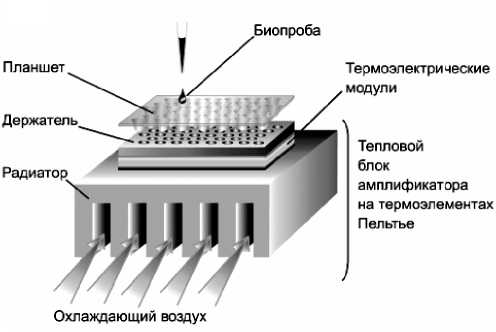
Рис. 1. Принципиальная схема прецизионного, программируемого устройства нагрева /охлаждения на ТЭБ представлена на рис. 1. Острая необходимость в разработке различных схем амплификато-ров с использованием ТЭБ потребовала создания методики численного расчета с целью моделирования рабочих процессов на виртуальной модели для создания эффективных устройств по следующим параметрам:

• •    точности поддержания температуры;

• •    потребляемой мощности;

• •    надежности работы ТЭБ (долговечности);

• •    рассеиванию тепла;

• •    уменьшению уровня шума;

• •    снижению расходуемых материалов;

• •    снижению себестоимости изделия.

Известные модели, в основе которых лежат зависимости типа (1), позволяют с достаточной степенью точности рассчитывать процессы в термоэлектрических устройствах, работающих в стационарном режиме (в условиях термодинамического равновесия, при этом параметры системы не зависят от времени). В данном устройстве время переходных процессов сопоставимо со временем стабилизации температуры, следовательно, подобный подход не применим для моделирования рабочих процессов.

ПОСТАНОВКА ЗАДАЧИ

Построение методики расчета термоэлектрического устройства в динамическом режиме заключается в разработке подхода совместного решения задачи нестационарной теплопроводности и теплообмена всех элементов и задачи описания термоэлектрических эффектов в ТЭБ методами неравновесной термодинамики [6]. Графически структура математической модели может быть представлена в виде, как на рис. 2.

Получение нестационарных уравнений тепловых источников в термоэлектрических элементах в зависимости от вектора плотности тока базируется на принципах, предложенных Осиповым [7]. Рассмотренный Осиповым вывод уравнения сохранения энергии для случая работы термопарного элемента в стационарном режиме был применен в данной работе для вывода нестационарных уравнений тепловых источников в термоэлементах.

Эффект охлаждения в твердом теле возникает в результате протекания по нему потока заряженных частиц (например, электрического тока), который непосредственно создает направленный тепловой поток и соответственно градиент температуры в охладителе (рис. 3). К этой группе можно отнести термоэлектрические эффекты, включая различные анизотропные, магнитотермоэлектрические и гальванотермомагнитные эффекты с учетом увеличения носителей заряда фононами; эффект охлаждения за счет переноса тепла инжектированными через p—n -переход неосновными носителями и др.

Эта группа физических эффектов охлаждения имеет ту особенность, что на их основе можно создать охладители непрерывного действия.

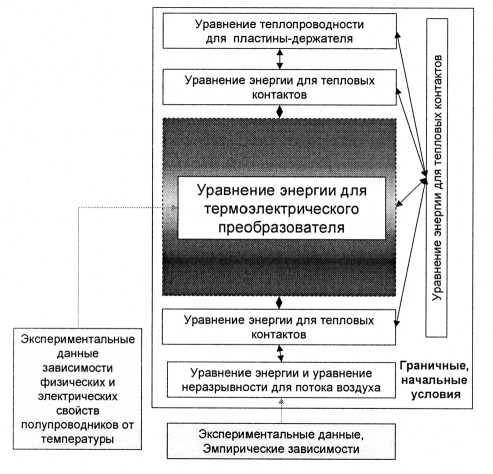
Рис. 2. Графическое представление математической модели расчета теплового блока амплифика-тора

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Закон сохранения энергии в нестационарном случае [7] имеет вид

^=- = - (qn)dQ + ц d^dA + e ф —dA + dt J             J 0 dt             dt vv

+ e J ( jE ) d A ,                             (2)

v где изменение энергии в элементарном объеме происходит по нескольким причинам:

• 1.    За счет потока тепла через поверхность объема v

• - J ( qn ) d Q ;

перейдем в первом интеграле к интегрированию по объему, тогда в соответствии с теоремой Гаусса получим

• - J ( qn ) d Q=- J div q d A ,            (3)

• 2.    За счет притока частиц (например, электронов и дырок)

• 3.    За счет перераспределения электрических зарядов, которое определим из выражения для потенциальной энергии частиц в объеме v , находящихся в электрическом поле с потенциалом ф ,

v где dA — элементарный объем.

J ц od^ dA , dt v где ц0 — химический потенциал.

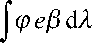
v

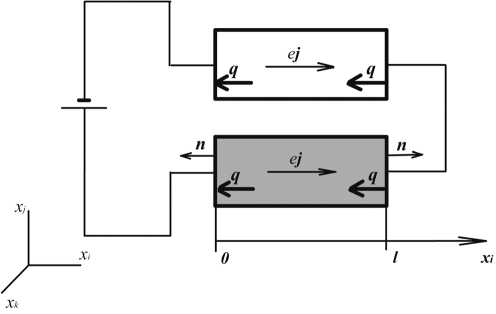
Рис. 3. Схематическое изображение термопарного полупроводникового элемента где e — электрический заряд частицы; отсюда следует, что изменение энергии за счет перераспределения частиц равно

I*феd^dA = e[фd^dA . dt            dt vv

Второй и третий интегралы можно объединить, если воспользоваться выражением для электрохимического потенциала

I"ц d^dA + e [ф d^dA = ц d^ dA,(4)

• 0    dt             dtd

vvv где ц — электрохимический потенциал, ц = ц0 + + eф. Если в дифференциальной форме баланса частиц [7]

d e

+ div j = b dt рассматривать случай отсутствия источника частиц, то, положив в уравнении b = 0, получим de        •

= - div i .

d t

Тогда выражение (4) преобразуется в f ц d^dA + e Гф d^dA =

• 0    dtd

vv

• =    -|(ц div j)dA.(5)

• 4. За счет работы, произведенной электрическим током,

v

J(e jE)dA = e J(jE)dA,(6)

vv где j = j(x, У, z, t) — плотность потока частиц, носителей электрических зарядов; E — напряженность электрического поля. Четвертый интеграл можно преобразовать, подставив вместо напряженности электрического поля его выражение через градиент электрохимического потенциала:

E = - 1 у ц .

e

Получаем e J(jE)dA = -J(jVц)dA.           (7)

vv

Введем плотность энергии w . Тогда dUv dt

= fd ^ d A . d t

v

Тогда

Таким образом, закон сохранения энергии в нестационарном случае можно записать

J dw dA = -J div q dX - vv

• д q     д     д Tд

divq = —i- =--Xik----+ e---П,,j, .(12)

ik                           ik k ^.

• дxi     дxi     дxk

Используя обобщенный закон электропровод ности (10), учитывая, что a = -J—, можно записать Рэ

- J ( ц div j ) d X - J ( j V ц ) d X .

vv

1 ди               _ д T

^-_:i     E i ~ ^р эik e к ^{+ a} ik 3—,         ⁽¹³⁾

e д x i                       д x k

В каждой точке системы существуют плотности потоков тепла и частиц, определяемых обобщенными законами электропроводности и теплопроводности:

e j = —о Vц - oa V T ,          (10)

e q = - X V T + П ej,                 (11)

где вводятся следующие тензоры:

• a — удельная электропроводность;

• a — термо-ЭДС;

• X — коэффициент теплопроводности;

П — коэффициент Пельтье.

Кинетические коэффициенты o , a , X и П не зависят от градиентов температур и электрохимического потенциала, а определяются свойствами конкретного материала. Между компонентами этих кинетических тензоров существует определенная связь, вытекающая из статистической механики. Эти связи называются соотношениями Онзагера:

oik = oki, Xik = Xki, где рэ — удельное электрическое сопротивление (Ом/м).

Тогда для третьего члена в уравнении (9):

■ дц       2     ■ ■ дT .        ....

j ^V ^ = Ji^" = - e P ik J k J i - e ^a ik     J‘ "     ⁽¹⁴⁾

^д x i                        ^{д Х} к

Аналогично для второго члена уравнения (9) можно записать

•     дJ цdiv j = ц —. дxi

Векторы j = [ j' ,0,0 ] и n = [ 1,0,0 ] . Подставляя выражения (12), (14) и (15) в уравнение (9), получаем следующую формулу закона сохранения энергии в нестационарном случае для однородной термоэлектрически анизотропной среды:

f ^ w d A = d t

v

= - J

д дT д , V_

Xik    + e^-ПikJk dX + дxi     дxk     дxi которые показывают, что в отсутствии магнитного поля тензоры а и X симметричны, а также

П» = Тай, которое связывает между собой компоненты тензоров Пельтье и термо-ЭДС.

Выражение (11) представляет собой обобщенный закон теплопроводности, т. к. учитывает перенос тепла, обусловленный не только градиентом температуры, но и переносом энергии частицами. Поток тепла Пельтье возникает благодаря переносу потоком частиц энтропии.

Для анизотропных тел выражение (11) раскрывается как

+ J

-

v V

2 _    • • e PikJkJi

-

д T . ^{e a} ik^ J i ^{d A} .

^д xk   )

Поскольку тензор Пельтье зависит от температуры

П» =П» ( T ) ,

получим

д n

^П ik ^J k д x i

„  д T ।       • qz- = - Xik 3— + eП ikjk. дxk

f8^) . -"i дх дx. , э t at, IA 1 7 T                 i.

J к +П»

^д / k д x i

Если рассматривать однородные термоэлектрически анизотропные проводники, то

П» П . ( T ),

( ^дП.)

дx,

V 1

J т

= 0.

Тогда уравнение (17) перепишется как

д п

^П ikJk д х.

дП 1к д T

д T д х

J_k +П ,к

^д j k д х ^.

Первый член правой части уравнения (21) представляет собой плотность тепла, выделяющегося в единицу времени за счет теплопроводности, второй член — плотность тепла Джоуля, третий и четвертый члены являются соответственно плотностями тепла Томсона и тепла Бриджмена. Пятый выражает выделение тепла при изменении плотности тока.

Коэффициент Томсона можно выразить, воспользовавшись соотношением Онзагера, которое еще называют вторым соотношением Томсона, и выражением (20):

Таким образом, уравнение закона сохранения энергии можно переписать в виде

k

T Ol д т "

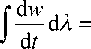
v

В случае однородной изотропной среды

X i. = X^{( T} ) 5 . , P i. = P ₃ 5 ik , ^T ik = TS ik , ^П 1. = ^. k .

-J

v

+J

V V

+J

v

д д T

^X ik Д ^{+ д} x i     ^д x k

+ е

Г дП1к д T

V

д T д x .

ц dj- d A + d x

^{1 J}

2 _     • • e PikJkJi

V

J_k +n_ft ^J д x,.

1 /

dA +

д T . ).-, ^e « ik^— Ji ^{d A} .

^{д x} k   J

Вносим в правой части все выражение под знак интеграла и упрощаем подынтегральное выражение

[ d A d A =f d t

v

v

д       "T . . _

4- Xik .. + e PikJkJi dA - дxi     дxk

-J

v

Здесь

^дП ki

-

V

д T

^a ik

д T . д x_i^il

^- e ⁿ ik

^д i k    „ ^d i i

ц дxi      dx i

d A .

дП ki

д T

^{- a} ik

-- ^ -7  ---- ik

тензор коэффициента Томсона, называемый также первым соотношением Томсона. Поэтому

f dA dA = f dt vv

д „ д T , . 4— X ik ^ ⁺ e P ikJkJi д X i д x .

-

-

д T - _n ^{e T} ik ^Ji ^- e ^П д x_i

дJk ik дxi

-

ц di. A d x _i

Тогда при суммировании в (21) остаются только диагональные элементы

fdA’ dA = dt

v

= j T" X(t)|T+e2 Рэ (t)Jij i j д xj       дx,- v

- eT ”j, - «пТА дx.         дx.

dA+

+ f ^ d ^J - d A .

^J d x

Примем для нашего случая d x . = d y . Тогда уравнение сохранения запишется в виде

[ d A d A = d t

v

= / XXT)X + e2P.(т)J2

V ^дy     дy

-

v

-

ет^J-enTA dA + дy       дy

+ I" ц -d ^J d A .

d y v

Таким образом, получаем уравнение для нахождения интегрального баланса энергии в бесконечно малом контрольном объеме полупроводникового изотропного элемента с током в нестационарном режиме работы.

Если на данном отрезке времени изменения плотности тока не происходит, то выражение для сохранения энергии упрощается и принимает вид

ЛщМ ^Рт^.и¹

^J dr , ЬчУ оу

V

V

^■^™

дТ - ет —у dZ .

ду

Подставляя соотношение Томсона из (22), в случае для изотропной среды получим

J dr

V

Д XzW^aP_+e'-_P,w j|_dy ду

^■^™

V

^■^™

Э«(Т)ЭТ .1 еТ———/ dz.

ЭТ dy _

РЕШЕНИЕ ЗАДАЧИ

В уравнении (24) записаны ки:

• Джоуля

тепловые

источни-

Рис. 4. Градиент температуры по высоте элемента Пельтье (AL — алюминиевая подложка, CU — медные спаи, P-N — эквивалентный (усредненный) полупроводниковый слой)

9 Д» = eW)f;

• Пельтье—Томсона

Уп-т -

—I

■el-------- dT

ЭТ .

Уравнение (25) позволяет проводить тепловой расчет с учетом источников в полупроводниковых элементах в нестационарных условиях, а также изменять:

(<5 у)^ — расстояние между узлами К и Р;

aPU - 7

^PU

^■^™

Хр

J Xz d£;

теплофизические свойства полупроводни- ков;

электрические свойства полупроводников;

закон изменения во времени плотности то- ка.

Полученное уравнение входит в состав математической модели, структура которой графически представлена на рис. 2. Данная математическая модель имеет только численное решение, реализуемое с помощью гибридного метода контрольного объема [8, 9]. Как было показано, дискретный аналог нестационарного уравнения энергии для твердого тела имеет вид

Q.рТр — и^Т^ + a_sT_s + U^T^y + ^Е^Е "*"

+ aNETNE + awsTws + aPUTPU + aPDTPD + b, где а Р — а ру + a s + qw + а' Е +

+ Gy + g ру + g РЕ) + а — S РДУ, ак = Хк / aPD"

р

— UzdS;

PD

^PD

*

_      __ ___ *__ b = 8СДУ + a TP ,

* Р с ДР а =-------

Ат

I

Тепловой источниковый член S_T = S_c + S_P Т для полупроводникового слоя описывается термоэлектрическими источниками (25) и (26), представленными в конечно-разностном виде.

Таким образом, мы получили методику, которая позволяет моделировать неравновесные термоэлектрические процессы в дифференциальной форме, с минимальными допущениями, с возможностью учета температурных зависимостей свойств полупроводниковых материалов.

Полученный метод позволил провести математическое моделирование процессов в термоэлектрическом амплификаторе. Сравнение полученных результатов численного моделирования и экспериментальных данных показало адекватность

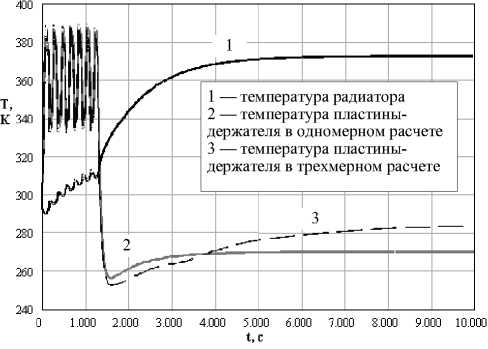
Рис. 5. Результаты расчета температуры пластины-держателя и радиатора по созданной методике созданной модели. Примеры результатов расчета представлены на рис. 4 и 5.

ЗАКЛЮЧЕНИЕ

Для расчета исполнительного устройства на термоэлектрических элементах Пельтье в динамическом режиме была разработана математическая модель и методика расчета тепловых источников. Методика позволяет численно моделировать термоэлектрические источники в дифференциальной форме, с минимальными допущениями, с возможностью учета температурных зависимостей свойств полупроводниковых материалов.