Метод математической индукции при доказательстве геометрических задач

В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений - это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

Математическая индукция— один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1.

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.

Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И, тем не менее, этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.

В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство \B\ + | BC | > | AC |.

Полная и неполная индукция

Индуктивное умозаключение – такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер.

Учитывая зависимость от характера исследования различают полную и неполную индукцию.

Полная индукция - это умозаключение, в котором общее заключение делается на базе изучения всех предметов или явлений данного класса. В этом случае рассуждение имеет следующую схему:

К примеру, установление того, что каждый из документов, необходимых для оценки готовности уголовного дела для передачи в суд, имеется, позволяет с полным основанием делать вывод, что дело следует передавать в суд

Полная индукция дает достоверное знание, так как заключение делается только о тех предметах или явлениях, которые перечислены в посылках. Но область применения полной индукции весьма ограничена.

Полную индукцию можно применить, когда появляется возможность иметь дело с замкнутым классом предметов, число элементов в котором является конечным и легко обозримым. Она предполагает наличие следующих условий:

• а)    точное знание числа предметов или явлений, подлежащих изучению;

• б)    убеждение, что признак принадлежит каждому элементу класса;

• в)    небольшое число элементов изучаемого класса;

• г)    целесообразность и рациональность.

Вот почему полная индукция чаще всего используется при расследовании уголовных дел, связанных с недостачей материальных ценностей. Здесь вывод осуществляется на базе подсчета всех без исключения содержащихся на складе или в хранилище предметов путем инвентаризации.

При этом в большинстве случаев юристу приходится иметь дело с такими однородными фактами, количество которых не ограничено или которые не все доступны в настоящее время для непосредственного изучения. Вот почему в таких случаях прибегают к использованию неполной индукции, которая на практике применяется значительно шире, чем полная.

Неполная индукция - это умозаключение, в котором на базе повторяемости признака у некоторых явлений определенного класса делается вывод о принадлежности этого признака всему классу явлений. Неполная индукция имеет следующую схему рассуждения:

Неполная индукция часто применяется в реальной жизни, так как позволяет делать заключения на базе анализа определенной части данного класса предметов, экономит время и силы человека. Правда, в данном случае мы получим вероятностное заключение, ĸᴏᴛᴏᴩᴏᴇ исходя из вида неполной индукции будет колебаться от менее вероятностного к более вероятностному.

Во многих разделах арифметики, алгебры, геометрии, анализа приходится доказывать истинность предложений А(n), зависящих от натуральной переменной. Доказательство истинности предложения А(п) для всех значений переменной часто удается провести методом математической индукции, который основан на следующем принципе.

Предложение А(п) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:

• 1.        Предложение А(п) истинно для п=1.

• 2.        Из предположения, что А(п) истинно для п=к (где k - любое

натуральное число), следует, что оно истинно и для следующего значения п=к+1.

Этот принцип называется принципом математической индукции. Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства.

Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения А(п) для всех натуральных п, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(к), попытаться доказать, что высказывание А(к+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(п) признается истинным для всех значений п.

Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

Наиболее естественное применение метода математической индукции в геометрии, близкое к использованию этого метода в теории чисел и в алгебре, -это применение к решению геометрических задач на вычисление.

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P (n),  зависящее от натурального числа n, справедливо для любого натурального n если:

• 1.       P (1) является истинным предложением (утверждением);

• 2.       P ( n )    остается истинным предложением (утверждением),

если n увеличить на единицу, то есть P ( n + 1) - истинное предложение (утверждение).

Таким образом метод математической индукции предполагает два этапа:

• 1.       Этап проверки:   проверяется, истинно ли предложение

• 2.       Этап доказательства: предполагается, что предложение P ( n ) истинно, и

• доказывается истинность предложения P(n + 1) (n увеличено на единицу).

(утверждение) P (1).

Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:

Пусть m - натуральное число, m > 1 и P ( n ) - предложение, зависящее от n , n >  m .

Если

• 1.        P ( m ) справедливо;

• 2.        P ( n )   будучи истинным предложением, влечет истинность

предложения P ( n + 1) для любого натурального n , n >  m , тогда P ( n ) - истинное предложение для любого натурального n , n >  m .

В дальнейшем рассмотрим примеры применения метода математической индукции.

Рассмотрим несколько примеров.

Пример 1. На сколько треугольников n-угольник (не обязательно выпуклый) может быть разбит своими непересекающимися диагоналями?

Решение.

Для треугольника это число равно единице (в треугольнике нельзя провести ни одной диагонали); для четырехугольника это число равно, очевидно, двум.

Предположим, что мы уже знаем, что каждый k-угольник, где k1А₂.А_П на треугольники.

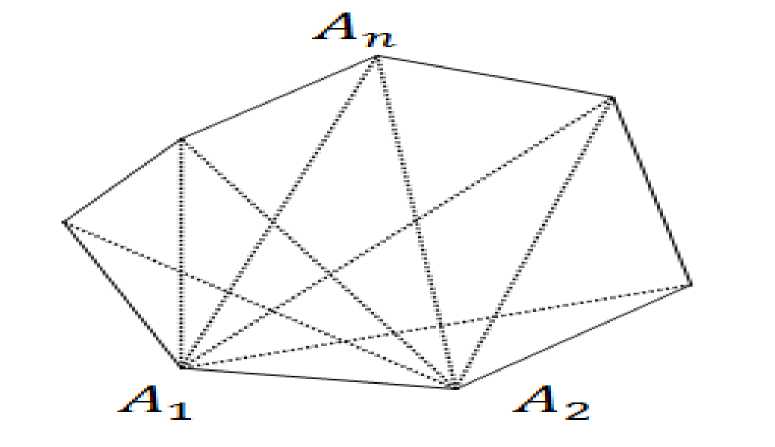
Пусть А₁А_к - одна из диагоналей этого разбиения; она делит n-угольник А 1 А₂^А_п на k-угольник A 1 A₂^A_k и (n-k+2)-угольник A₁A_kA_k+1^A_n. В силу сделанного предположения, общее число треугольников разбиения будет равно (k-2)+[(n-k+2)-2]=n-2;

тем самым наше утверждение доказано для всех n.

Пример 2. Вычислить сторону а₂ п правильного 2 n -угольника, вписанного в окружность радиуса R .

Решение. При n = 2, правильный 2 ² -угольник есть квадрат, и в этом случае a ₄ = R

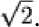
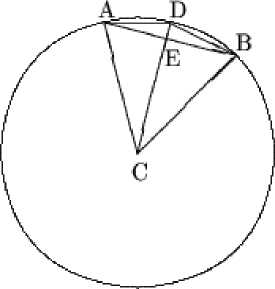
Пусть а₂ п = а и определим а₂ п+1 = а Если AB = d , то AE = d /₂; BD = а . По теореме Пифагора, из прямоугольного треугольника DEB

а'=© + DE2

В свою очередь DE = R - EC и

Таким

DE=R-^R2-^)’

EC2 = ВС2 - BE2

и, следовательно,

= R2

-

образом,

a2"+i=Ji) ^-/^-GO = J*2 - 2RjR2-l- формула перехода от n к n + 1.

В частных случаях

a^ — R42 —— cig

= Lr2 - 2R/R2

R2 • 2

— R^2 - V2.

a₁₆ — ^2R²-2R /r²-

1r2(2 -42) —r /2- J2 + V2.

Возникает гипотеза

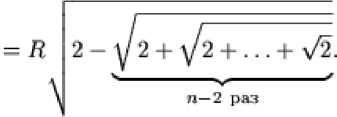
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2)

выполняется при n = k . Вычислим ■_■  . Согласно формуле перехода,

откуда следует, что формула (1) справедлива при всех n.

Замечание. Из (2) следует, что длина окружности равна

и, поскольку I = 2nR , получим

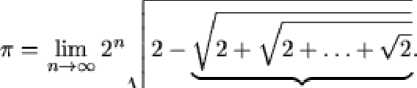
п— 1 рал