Метод моделирования цифровых полутоновых изображений

Сейчас трудно найти научно-техническую область, где бы в той или иной форме не встречались прикладные задачи цифровой обработки изображений. Переход к ЦПИ, представленных малоразрядными двоичными числами (4-8 разрядов) резко расширил возможности использования изображений как наиболее емкого носителя различного рода информации. При передаче изображений на расстояние под действием шумов в канале связи ЦПИ разрушаются, и тем больше, чем больше интенсивность шумов.

Для разработки и исследования алгоритмов восстановления (фильтрации) ЦПИ и их ВП, представляющих собой многомерные случайные процессы, необходимо располагать ММ, адекватными реальным процессам. К настоящему времени разработано большое число различных ММ двумерных изображений [1-5], подавляющее большинство которых требуют больших вычислительных ресурсов. Работ, посвященных ММ ВП ЦПИ немного, в основном это работы по построению ММ на основе многомерных непрерывных по значениям и дискретных по времени гауссовских марковских процессов (МП) [6-11]. Структура таких ММ проста и физически ясна, но реализация их даже в трехмерном варианте по заключению самих авторов требует чрезмерно больших вычислительных ресурсов.

К ММ предъявляются два основных требования – наиболее точное соответствие модели реальным процессам и минимальные вычислительные ресурсы на ее реализацию. Эти требования являются противоречивыми, так как при стремлении точно описать реальный процесс приходится усложнять ММ и соответственно увеличивать ресурсы на ее реализацию. При построении ММ ВП ЦПИ компромиссным решением может быть построение ММ на основе дискретнозначного ММП. В этом случае, если фильтрация изобра-

жения осуществляется сразу после получения его из канала связи, то отталкиваясь от каузально расположенного множества ранее принятых элементов изображения, наибольший эффект может быть достигнут при рекурсивной нелинейной фильтрации [12]. Поэтому в качестве ММ ВП ЦПИ возьмем многомерную многозначную цепь Маркова (ЦМ).

Постановка задачи

Пусть статистически связанные ВП ЦПИ представляют собой дискретнозначный ММ ^ ( i , j ..., q ) , где i, j,..., q - дискретные координаты, с разделимой корреляционной функцией вида:

r ( k , l ,..., s ) = a^ exp{-a i |k| -a ₂ |l|,..., -a q |s|} , (1) где σ μ² – дисперсия многомерного процесса; _a i ( i = 1, q) _— множители, зависящие от ширины спектральной плотности мощности случайных процессов по каждой из координат.

Необходимо построить ММ ВП ЦПИ на основе ММП. Будем считать в соответствии с (1), что д ( i , j ..., q ) представляет собой суперпозицию q одномерных дискретнозначных МП с нескольки-

ми значениями.

При цифровом представлении q -мерных слу-

чайных дискретнозначных МП двоичными g-раз-

рядными числами

у. .     = (у ^{( 1 )}

yi, j ,..., q          y i , j ,..., q

у ^{( 2 )} yl, j,.

-, q

У ⁽ g)    )

•yi, j,...,q

каждый разряд У^,.,._д ( l = 1, g ) можно рассматривать как случайную последовательность двоичных символов 0 и 1, а оцифрованный многомерный МП адекватный статистически связанным ВП ЦПИ как сумму последовательностей разрядных двоичных изображений (РДИ). Причем, статистическая избыточность, свойственная коррелированному ММП, присуща также и двоичным сечениям, на которые он разбивается [12].

Представляя ВП ЦПИ набором и g РДИ, сведем задачу построения ММ ВП ЦПИ к ММ видеопоследовательностей РДИ, каждая из которых представляет собой q -мерную ЦМ с двумя равновероятными ( py ¹ = p^ ) ) значениями M ^ ¹ ) , M 2l ) и матрицей вероятностей переходов (МВП) из одного состояния в другое n ^{( l} ) ( l = 1, g ) .

Для демонстрации метода построения ММ ВП ЦПИ на основе многозначного ММП ограничимся построением ММ одной и двух статистически связанных ВП ЦПИ, представляющих со-

бой трехмерный и четырехмерный многозначные МП.

Математическая модель последовательности РДИ

Будем считать, что последовательность кадров l -го РДИ представляет собой трехмерный дискрет-нозначныйМП { Ц ( l ) ( i, j, k ) } с двумя пространственными координатами ( i, j ; i = 1, m, j = 1, n , l = 1, g ) и третьей – временной k = 1,2…, связанной с номером кадра в последовательности l -го РДИ.

В соответствии c (1) ВП l-го РДИ можно представить как суперпозицию трех одномерных дискретнозначных МП с двумя равновероятными (pf = p2)) значениями M1(1), M^ и МВП от одного состояния в другое внутри кадра l-го РДИ 1П(1) =||'п^|, 2П(1) =||2пj)||, i, j g 2, l g g и между соседними кадрами 4П(1) =|14п«I|, i, j = 1,2,l = 1,g , соответственно. Элементы матриц 4 n(l) и 8 П(1) одинаковые для всех (1 = 1, g).

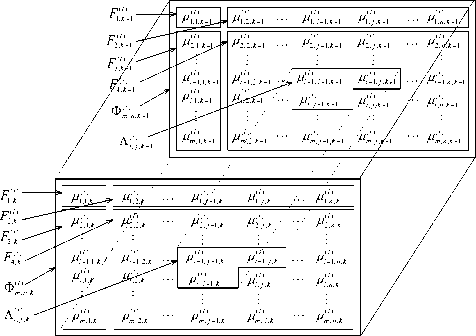
Рис. 1. Области ОМСП двух кадров ЦПИ с окрестностью из трех элементов

Выберем в качестве ММ l -го РДИ в k -том кадре одностороннее марковское случайное поле (ОМСП) на несимметричной полуплоскости (НСПП) (рис. 1) с окрестностью элемента p j

Л 1 ) л = { j , M i^ j , k , <  j -„ } ,     (6)

[0 ,

Л -

{ ( i — 1, j,^k ) } , { ( i , j — 1 ) , k } ,

{ ( i , j ^{-1, k} ) , ( i^-1,j , ^k ) ^, ( i^-1, j ^{-1, k} ) } ,

пРи ( i , j ) ^e F l ) при ( i , j ) ^e F l ) при ( i , j ) ^e F k пРи ( i , j ) ^e F?

где F ikl ) e F k , i = 1,4 .

Рассмотрим случай, когда моделированию подлежит случайный двоичный элемент p j l - го РДИ в k -м кадре (см. рис. 1), принадлежащий области F ₄ ⁽ k ⁾ g F _{4 k} . Моделирование элементов l -го

РДИ, принадлежащих областям F kl ’ , F ₂ ⁽ k ’ и F¹ ’ проще, чем области F ₄ ⁽ k ’ и сводится к моделированию одномерных и двумерных стационарных ЦМ []. Окрестность элемента v * l ⁾ = pflj _k l -го РДИ с учетом элементов соседнего кадра l -го РДИ составляет семь соседних элементов (рис. 2).

Л£ ,k = {< ; v 2l) ; v <¹) ; v^ ; v ^ ; v ^ ) ; v ‘ ^{( 1 )} } , (7)

где

V ^(l ) ₌ „( l )         ) ₌ „( l )           ₌^{( l} )

^V 1        H i, j - 1, k , ^v 2       ^H i-1, j,k , ^v 3       H i - 1, j - 1, k ,

V^(l ) ₌ „^{( l} ) _v'^{( l} ) ₌ „^{( l} ) _v'^{( l} ) ₌ „^{( l} )

^V 4 ^H i, j,k , ^V 1 ^H i, j-1,k - 1 , ^V 2 ^H i - 1, j,k - 1 ,       (8)

_v'^(l ) ₌ „^{( l} )          _v'^{( l} ) ₌ „^{( l} )

^v 3        ^H i-1, j-1,k - 1 , ^v 4        ^H i, j,k - 1 •

Сплошными и пунктирными линиями на рис. 2 указаны статистические связи между элементами РДИ, входящими в окрестность Л\¹ j _k элемента v 4^ ⁾ .

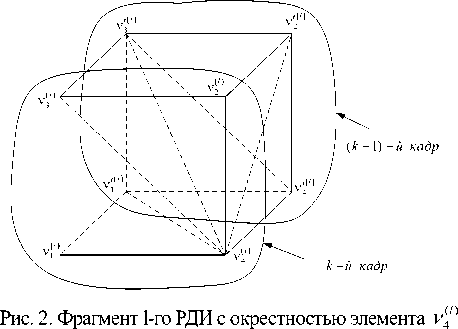
Появление значений элемента v 4 ( l ) = M^^ или v 4 ) = M 2 l ) зависит от количества взаимной информации между элементом v ^t( ) l -го РДИ и элементами окрестности (7), которое определяется выражением [13]

I ( у(‘ ) ,V«, V 4⁽l⁾ , V 4l⁾ ) =

_w(v (l ) (l ) v^(l ) i/^(l) 1/^,(1 ) v'(l ) v'(l ) v'^v ’1 (9) _ lo w y y 4 I ^V 1 , ^v 2 , ^v 3 , ^V 1 , ^v 2 , ^v 3 , ^v 4 ) ⁽⁹ 7 “ Wv 4l ’| v ' l ’ , v 2^y ’ ,v 3l’ , v ‘ ⁽ ’ ) '

В условной плотности вероятности w(V(l ) lv^f(l ) v'⁽l ) ) v'⁽l ) 1 чттрм put i/^f(l) етятт/тетт/Г ^{ww v} 4 ^v i , ^v 2 , ^v з , ^v з элемент v ₃ , статистически связан с элементами v 3l⁾ , v ,^(l) , v 2l⁾ , что недопустимо для сложной ЦМ. Убрав эту связь, выражение (9) можно представить в виде

I ( v ,⁽ l ⁾ , v 2 l ) , V ‘ ) ,V« ) =

.     w(v 4l)|v1(l)) ■ w(v 4l v )) x g w(v4° | v3(l)) ■ w(v4° | v;y))             (10)

_x w( v 4 l ) | v 3^{( l} ) ) ■ w(v 4 l ) | v 44^{( l} ) )

w( v 4 l ) | v1^u ) ) ■ w(v 4 l ) | v ₂'^{( l} ) )

Сложная ЦМ, которую образует окрестность

(7) с элементом v4^) l-го РДИ, полностью опреде- ляется вероятностями pl), рУ) и МВП П(1), элементы которой имеют вид

П jimnqr = П ^{( l )} ( v У ⁾ = MУ ⁾ | v , ^{( l )} = M ^, v 2l ⁾ = M У ⁾ ;

V у ) = M ( ) ; v ‘ l’ = MУ ) ; v ‘ l’ = M У ⁾ ;        (_U)

v ‘ l ⁾ = M q ⁾ ; V ₄ ' ^{( l )} = M y ⁾ ), i , j , k , l , m , n , q , r = 1,2.

При известных матрицах ’ n ^{( l )} , ² П ^{( 1 )} , ⁴ П ^{( 1 )} для вычисления элементов матрицы П ^{( l )} (11) необходимо предварительно вычислить матрицы

³ n ^{( l )} = ¹ П ^{( l )} • ² П ^{( l )} ;

• ⁵    П ^{( 1} ) = 1 П ^{( 1} ) • ⁴ П ^{( 1} ) ;

• ⁶    П ^{( 1} ) = ² п ^{( 1 )} • ⁴ П ^{( l )} ■                              ⁽¹²⁾

• ⁷    П ^{( 1 )} = ³ П ^{( l )} • ⁴ n ^{( l )} = 1 n ^{( l )} • ² n ^{( l )} • ⁴ n ^{( l )}

• 3.    Из первого столбца матрицы П ^{( 1} ) выбирается элемент a s ^{( l )} ( s = 1,8) , соответствующий значениям элементов окрестности Л ⁽ |j _k ;

• 4.    Число 5^ сравнивается с выбранным элементом а У ) ( s = 1,8) и ^ У ) <  а^{( )} , то элемент изображения v У ⁾ принимает значение v У ⁾ = M , ^{( l )} = 0 , в противном случае v 4У ⁾ = M У ⁾ = 1 ;

• 5.    Если i, где K – длина ВП, -переход к п.3, иначе п.6;

• 6.    Останов.

определяющие попарную статистическую связь элемента v У ⁾ с элементами v ₃ ^{( l )} ,V _X ’ ^{1 )} , v 2 ^{( l )} , v ₃ ‘ ^{( l )} соответственно.

Используя энтропийный подход к попарно статистически связанным элементам последова-

На рис. 3 представлены 1 и 5 кадры в ВП искусственных РДИ размером 256х256, полученных с помощью разработанной ММ при условии, что матрицы ’ П ^{( 1 )} , ² П ^{( 1 )} , ⁴П^{( 1 )} равны, с элементами 1п( l ⁾ = ²п i l l ⁾ = = ⁴п ( l ⁾ = 0,9 ( i е 2 ) , из которых видно, что структура искусственных изображений однородна,чтоподтверждаютоценки 1 п * и ²п*. , вычисленные по искусственным PДИ в каждом из приведенных кадров l -й ВП.

тельности l -го РДИ, запишем МВП для сложной ЦМ в виде:

n ( l ) =	У П (lL. iiiiiiii П (l).... iiijiiii	П (l ’...? jiiiiiii П ( l L.. jiijiiii		'оу Х ау Х	аУ1 Х )
					а 2 ‘ ( 1 Х
	п (17... jiijiiii	п ( l X.... jjjiiiii	⎟=	аУ	а 7 ‘ ( 1 Х	, i , j = 1,2; i * j . (13)
	п (12... ⎝ ijjjiiii	п ( l ‘Х.... jjjjiiii ⎠		alX X < а 8	аУ' \ 8

Значения элементов матрицы П(l) (13) мо- гут быть вычислены с учетом матриц

Например, выражения для вычисления ментов первой строки матрицы П(l)

(12). эле-при

Кадр 1 ¹п * = 0,8979; ²п * = 0,89936

1 n ^{( l )} = ² n ^{( l} ) = ⁴ п ^{( l} ) =

0,9

0,1

0,1

0,9

имеют вид

It (l I...

iiiiiiii

1^(1) 2 (1) 4 (1 ) 7(1)

π⋅π⋅π⋅π ij ij ij ij

3(1 ) 5 (1 ) 6(1 )                    "'                   ^,

π _ii ⋅π _ii ⋅π _ii

П (l L- jiiiiiii

1„(l)    2„,(1 ) 4   (1)    7 (1)

π⋅π⋅π⋅π ij ij ij ij

3(1) 5(1 ) 6(1 )                                   ^,

π _ii ⋅π _ii ⋅π _ii

i≠j.

Вычисление остальных элементов матрицы П ^{( l )} осуществляется в соответствии со значениями элементов окрестности Л.уy_t.

Алгоритм      формированияпоследовательности марковских РДИ

Моделирование ВП l -го РДИ состоит из 6 следующих этапов.

• 1.    Задаются МВП ’ П ^{( l )} , ² П ^{( 1 )} , ⁴П^{( l )} , вычисляются матрицы ³ П ^{( 1 )} , ⁵ П ^{( 1 )} , ⁶ П ^{( l )} , ⁷ П ^{( 1 )} и матрица П ^{( l} ) ;

• 2.    Берется случайное число ^ r ^l l ( _r <  _m . n ) , равномерно распределенное на интервале [0,1];

Кадр 5 ' п * = 0,8993; ² п * = 0,897

Рис. 3. Искусственные РДИ в различных кадрах

Проведены исследования ММ ВП l -го PДИ для различных статистических связей между соседними элементами l -го РДИ в пространстве (кадре) и времени (между кадрами), показавшие

высокую адекватность аналогичным l -м РДИ реальных 8-разрядных ЦПИ.

Математическая модель видеопоследовательности ЦПИ

Математическая модель ВП ЦПИ представляет собой трехмерную ЦМ с q = 2 ^g значениями и состоит из g ММ ВП РДИ, упорядоченных по разрядам двоичных чисел представления ЦПИ. Объединение РДИ в ЦПИ в каждом кадре ВП осуществляется на g -разрядном регистре и не требует вычислительных операций. Объем памяти при этом не превышает размера одного кадра ЦПИ. При моделировании ЦПИ необходимо учитывать, что каждое l -е РДИ имеет свои индивидуальные разрядные МВП, полученные на большом количестве реальных ЦПИ [14].

На рис. 4 приведены 1 и 10 кадры ВП искусственных ЦПИ при значениях элементов матриц     ’ П ^{( 1 )} , ² П ^{( 1 )} , ⁴П^{( 1 )} , равных 1 п ( 1 ) = ²п ( 1 ) = 0,6 ,

1 п ( 2 ) = ²я^ ) = 0,65 , '4 )= ²я^³ ) = 0,7 , 14 ) = ²п < ⁴ ) = 0,75 1 п ^{( 5} ) = ²л^ ) = 0,8 ,    ^⁶ )= 2л^ ) = 0,85 , П^ )= 2^ >= 0,9

1 п ^{( 8 )} = ²п ^{( 8 )} = 0,95 и ⁴п^⁾ = 0,9 для всех l = 1, g .

Математическая модель двух статистически связанных ВП РДИ

Чем больше размерность случайного процесса, тем сложнее привести пример его физической реализации. Будем считать, что трехмерный случайный двоичный МП, описанный ранее, перемещается в пространстве от позиции d -1 к позиции d дискретно с равными интервалами, фиксируя изображения одного и того же объекта с двух разных позиций.

Представим марковское ЦПИ размером m х n элементов как сумму из g РДИ. По аналогии с предыдущей ММ построим ММ двух статистически связанных ВП l -ых РДИ. Пусть { ^"j k d } является процессом l -го ( 1 = 1, g ) РДИ двух статистически связанных ЦПИ в k -м кадре в позиции d и представляет собой суперпозицию четырех одномерных двоичных МП с двумя равновероятными ( P i ⁾ = P 2 ⁾ ) значениями M j ^{( l )} , M ⁾ и МВП от одного значения к другому внутри кадра ( ’ П ^{( l} ) , ²П ^{( l} ) ), от кадра к кадру ( ⁴ П ^{( l} ) ) и от позиции к позиции ( ⁸ П ^{( 1} ) =||⁸ п^ |, i , j = 1,2, l = 17 g ). Матрицы ⁴П ^{( 1 )} и ⁸П ^{( 1} ) для всех l е g постоянны.

1 кадр

10 кадр

Рис. 4. Кадры искусственной видеопоследовательности ЦПИ

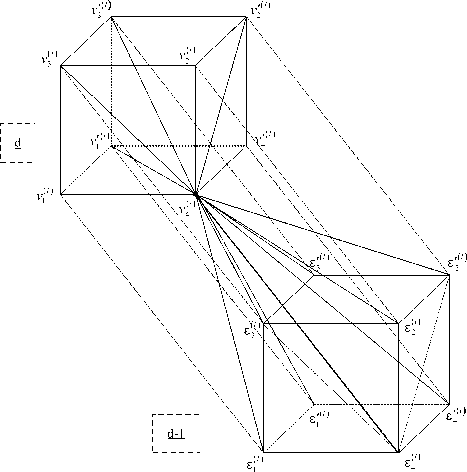
Рис. 5. Фрагмент двух статистически связанных последовательностей l -х РДИ

Элементы l -го РДИ в позиции d (рис. 5) обозначим через v ^ ⁾ = ^.м , ^v 2 l ⁾ = P i - L. k , d ,

V (l ) = U) )                 V)^ ) V 3       P i - 1, j - 1, k , d ,        V 4	= u (l ) P i, j,k,d ,	v'(l ) =     ) V 1         P i , j - 1, k - 1, d ,
(l ) = „( l )            V'W = V 2        P i- \, j , k- 1, d ,    V 3	( l ) P i - 1, j - 1, k - 1, d ,	( l )           ( l )               я V 4       P i,j,k - 1,d , а
через         к,1 ) = plj	- 1, k , d - 1 ,	£ (l ) = U) ) к 2       p i - 1, j , k , d - 1 ,
( l )             ( l )                                  ( l ). ь 3       P i - 1, j - 1, k , d - 1 , b 4	= ^ ilk , d — 1 ,	( l )             ( l ) 6 1         p i , j - 1, k - 1, d - 1 ,

• ⁽ l ⁾ = U) ⁾                 £-'⁽l )        ⁽ l )                     f'⁽l ) = и

' 2        Pi-1, j ,k - 1, d - 1 , ^c 3     = Pi-1, j - 1, k - 1, d - 1 ,     ^c 4        Pi, j,k - 1, d - 1

элементы изображения в позиции ^{d - 1 .} .

Окрестность элемента vУ ⁾ l -го РДИ в позиции d составляет 15 соседних элементов соседних l -х РДИ (рис. 5)

л" = К ⁾ ,v; > ,v ;-x" ⁾ ,v «- ,v «⁾ ,v «- ....

Pll ) p- ) p- ) p- ) p'M ) р'У ) р'У) р'У)

... 6 ] , ⁶ 2 , ⁶ 3 , ⁶ 4 , ⁶ ] , ⁶ 2 ’ ⁶ 3 ’ ⁶ 4 )

Будем считать, что заданы МВП для трехмерного ’ П ^{( l )} , ² n ^{( l )} , ⁴ П ^{( 1 )} в позиции d и аналогичные МВП ’ п^{, ( 1 )} , ² П' ^{( 1 )} , ⁴ П' ^{( 1 )} для трехмерного МП в позиции d -1, статистическая связь между трехмерными процессами в позициях d и d-1 характеризуется МВП ⁸ п ^{( l )} . Тогда для моделирования четырехмерного МП потребуется 15 переходных

Количество информации, определяющей появление того или иного значения элемента v 4 ) l -го РДИ в позиции d , должно зависеть лишь от статистических связей между элементом v 4 ) и элементами vf ’ , v * ^{l )} , v ‘^l ’ , s У’ окрестности (16) и определяется выражением вида

I ^) , V 2^{l )} , V ‘ ) , V <2 , 8 <^l) ) =

l ) „w (^V4 I ^V1 ^,V2 ^,V3 ^,V1^,V2 ^,V3 ^,V4 ••• log----------;------------------------------------

• 1 )    „<1) „'<1) „'<1) „'<1)

w (V 4 |V3 ,V1 ,V 2 ,V3 ••• pl)) PH РУ) PH р'У) р'У) р'У) р'У)

•••81  , 8 2  , 83  ,84  , 81   , 8 2   ,8 3   ,84   )

pl) ) p) ) p) ) p) ) р'У ) p)(t ) _Р'У ) _Р-У)

••81   , 82  , 83  , 84  , 81    , 82   , 83   , 84

w(v <^l) lv'<^l) s'^v ) s'^v ) s^w s'^{) ) 1 w v 4 v 3 , ⁸ 1 , ⁸ 2 , ⁸ 3 , ⁸ 3

• x—-----------;---------;•

• ll)    L'll)

w (v

матриц вида:

' П ^(l) , ' П'¹⁷⁾ , ² П ⁽¹⁾ , ² П^,(1) , ⁴ П ⁽¹⁾ , ⁴ П^,(1) ,

³ п ^(l ) = ' П^,(1) X ²П^,(1) ,

³п^,(1 ) = ' П^,(1 ) X ²П^,(1 ) ,

⁹ П ^{( 1 )} = ³П^{,( 1 )} х ⁸ П ^{( l )} ;

¹⁰ П ^{( 1} ) = ⁵П^{,( 1} ) х ⁸ П ^{( 1} ) ;

^ПП^{( 1} ) = ⁶П^{,( 1} ) х ⁸ П ^{( 1} ) ;

¹² П ^{( 1} ) = ⁷П^{,( 1 )} х ⁸ П ^{( 1} ) ;           (20)

• ⁵ П ^(l) , ⁵П^,(1) = ' П'¹⁷⁾ х ⁴П'¹⁷⁾ ;

• ⁶ П ⁽¹ ) ⁶П'⁽¹ ) = ²П'⁽¹ ) _х ⁴П'⁽¹ ) ■

• ⁷ П ^(l ) , ⁷П'¹⁷ ) = ³П^,(1) х ⁴П'¹⁷ ) ;

• ¹³ П ^{( l )} = 'П'¹⁷⁾ х ⁸ П ^{( l )} ;

• ¹⁴ П ^{( 1} ) = ²П'^{( 1 )} х ⁸ П ^{( 1} ) ;

¹⁵ П ^{( l} ) = ⁴П'¹⁷) х ⁸ П ^{( l} ) .

Для выполнения условия взаимной независимости элементов окрестности Λ_ijkd преобразуем выражение (17) к виду

I (v? ’ ,V У’ ,V ‘ l ) , 8 4 ) ) =

= 1o w(v4)|v1))w(v4)|v2l))w(v4)|v4(l)) x g w(v 4 )|v3(l) )w(v 4 )|v;(l) )w(v4 )|v2(l))

_x w ⁽v 4 l ⁾ I 8 4 ⁾ ) w ⁽v 4 ⁾ I 8 ’ ^{1 )} ) _x             ⁽¹⁸⁾

w ( v 4 ) | 8,^(l ) ) w ( v 4 ) | 8 2 ) )

_x w ( v 4 ) | 8‘^l ) ) w (v 4 ) | 8 ^ ) ) w (v 4 ) | v 3^{( l} ) ) w ( v 4 ) | 8 4^{( l} ) ) w (v 4 ^l ) | 8 3⁽⁽ ) )

Уравнение (18) является основой для построения ММ четырехмерного дискретнозначного МП с двумя значениями.

Вероятности переходов от значений элементов окрестности (16) к значению элемент v 4 ) в позиции d , для дискретнозначного четырехмерного МП определяются МВП П ^{( l} ) , элементы которой имеют вид:

Вероятности появления элемента v 4( l ’ l -го РДИ со значением v 4 ⁾ = M , ^{( l )} или v 4 ⁾ = M 2 l ⁾ зависят от комбинаций значений элементов РДИ, входящих в окрестность (16), и образуют матрицу

П ^{( l )} =

. ( i )

^iii---H

^п iiiijii — ii

71⁽ ) ⁿ ijjjijj ™

1.-

П ⁽ ) щО---.у

1—.—'

71' '

^П jiiiiii — ii

71 '

^П jiiijii^ii

- (l)

J'jjji^-JJ

¹ .'

. (l )

j;'mjj—J

¹ —.—'

i , j = 1, 2; i * j

Значения элементов матрицы П ^{( l )} могут быть вычислены в соответствии с аргументом логарифма (18), используя энтропию между генерируемым элементом v 4 ⁾ в позиции d и взаимоне-зависимыми элементами окрестности Л * ¹j _{k d} . Например, при известных значениях матриц (20), выражения для вычисления элементов первой строки матрицы П ^{( l} ) имеют вид:

П ^{1 1} )              = П (v <^{l )} |v ^(l) = M ^(l) ;v ₃ ^(l) = M (‘ ⁾ ;

ijklmnqrtsfhuvpw         \ 4 I 1            j 3            k v311) = M(l) ;v4(l) = Mn) ;v‘l) = M^;

8 _X = M t ; 8 1 ) = ( l ⁾ Mt‘ ) ; 8 « = M(; ) ; 8 « = M hl ) ; (19) ^ ‘ l ⁾ = M W ) ; 8 ’- ) = M Vl ) ; 8 ’- ) = M Pl ) ; 8 4^{( l )} = M W¹ ) ),

7Г (l ) ^п iiiiiii — ii

•. ■

1_(l) 2_(l) 4(l ) 8(l ) 7   (l ) 9 (l) 10„(1) 11 (l)

^π ij ^π ij ^π ij ^π ij ^π ij ^π ij     ^π ij     ^π ij

³ п ) ⁵ n <;) ⁶ n ⁽ ‘ ) ¹³ n ⁽ ‘ ) ¹⁴ п ⁾¹⁵^ ‘) ¹² n^ ‘ )

₍ 1)        ¹ n j ⁾² n j ⁾⁴ n j ⁾⁸ n j ⁾⁷ n j’’ n ⁷¹ )" n j)" n j l) (22)

ⁿ ymiii ^ ii          3 (1 ) 5 (1) 6(1 )V3„,(1 ) 14 (1 )1S(1) 12 (1) ’

—       ⁿ;. ⁿ;. ⁿ;.    ⁿ ;.    ^ i.    ^ i.   ^п;.

i , j , k , l , m , n , q , r , t , s , f , h , u , v , p , w = 1,2.

i * j -

Вероятность п ^l i ‘ ⁾ _i при условии, что

1 п ( l ) = ² п ^{( 1} ) = ⁴ п ( l ) = 1 n‘ ( l )

= ² n‘ ( l ) = ⁴ n‘ ^{( l} ) = ⁸ п ( l ) =

⎛ 0,9

^⎜⎝ 0,1

0,1

0,9

П^ L =1 1 - (0,¹) ⁴ (0,^{756) 4} = 0,9998494 , “г     (0,82) ⁶ 0,7048

j _M = 0,0001506 .

Остальные элементы вычисляются аналогично в зависимости от комбинаций значений элементов окрестности A ilj _k d .

Исключая соответствующие МВП из формул (22), легко получить матрицу П ^{( l )} для ММ меньшей размерности.

Алгоритм формирования статистически связанных ВП марковских РДИ

Алгоритм работы ММ аналогичен алгоритму работы трехмерной ММ.

Математическая модель двух статистически связанных ВП ЦПИ

Математическая модель статистически связанных ВП ЦПИ, представленных g -разрядными двоичными числами, формируется простой поразрядной записью значений элементов g РДИ в g -разрядный регистр двоичного числа, представляющего собой выборку четырехмерного многозначного МП.

1 кадр d -1

последовательности

1 кадр d последовательности

5 кадр d -1

последовательности

Рис.6. Кадры искусственных статистически связанных видеопоследовательностей ЦПИ в позициях d -1 и d

5 кадр d последовательности

На рис. 6 представлены 1 и 5 кадры двух статистически связанных ВП искусственных ЦПИ, полученных с помощью разработанной ММ для * п ( 1 ) = ²п ( 1 ) = 0,6 , *п ( ^{2 )} = ² п * ^{2 )} = 0,65 , 1 п ^{( 3} ) = 2^ ) = 0,7 , ^ = ² п ( 4 ) = 0,75 П^ ) = 2^ ) = 0,8 , 1^ = ² п^) = 0,85 , 1 я ; * ^{7 )} = ² п< ^{7 )} = 0,9 и 4л^ ‘ ) = ⁸ п^ ) = 0,9 .

Важной особенностью ММ является отсутствие вычислительных операций при генерации искусственного ЦПИ в k -м кадре в позиции d .

Выводы

Из анализа результатов полученных для трехмерной и четырехмерной ММ следует, что при одних и тех же статистических характеристиках составляющих случайного процесса, его статистическая избыточность возрастает с увеличением размерности процесса. Если в одномерном случае вероятность появления одного и того же значения элемента изображения по строке (столбцу) равна п ^{( l )} = 0,9 , то в двухмерном (первый кадр) п ( l ) = 0,9878 , в трехмерном ^п = 0, ⁹⁹⁹⁵ 6 , в четырехмерном п ( = 0,9998478 [14] Откуда ¹.

следует, что статистически связанные ВП ЦПИ могут обладать очень большой статистической избыточностью, которую целесообразно использовать при обработке ЦПИ.

Аргументы уравнений (1 1) и (19) позволяют однозначно определить структуру алгоритмов фильтрации l -х РДИ реальных ЦПИ, что было успешно использовано при синтезе и исследовании алгоритмов нелинейной фильтрации ЦПИ в условиях действия белого гауссовского шума. Результаты исследований опубликованы в трудах различных конференций и журналах, в том числе в работах [12; 15-16].