Метод модельного представления спектров

ММПС позволяет избежать некоторых трудностей, связанных с численным интегрированием тонкой структуры спектра. Для модели равностоящих линий одинаковой интенсивности Эльзассера ФСП имеет вид:

^т = 1 - sh |? exp ^{( -} ych ^e ) J 0 ⁽ iy ) dy                           ⁽ 1)

где y = s to / dsh в = x/ sh в , в = 2na / d , J ( iy ) - функция Бесселя нулевого порядка, d – расстояние между линиями.

Пользуясь представлением интеграла Эльзассера в виде рядов, легко получить при β ≥ 3

τ = exp [ - x ] .                                         (2)

Для больших значений параметра y :

т = 1 -Ф

^Л / xch в- 1 )     sh в

Л sh ^в J 7( ch в — 1 ) ^.

Если в ^ 0, то

τ

= 1 - Ф f П s to

к d      J

~ 1 - д/x/2п .

Для статистической модели

^т = exp

z 1----- J JQ(S)[1 - exp(sbv (a)to)dvds d J Q ( S) dS f 0

-f

• (3)

• (4)

• (5)

В (5) Q(S) d S – вероятность того, что линия имеет интенсивность

в пределах от S до S + dS .

Для дисперсионного контура линии

Q 1 ^{( S} ) = ^1exp S

f-

Sl Q2(s)=§ (s - s) ,

к S J

где S –средняя интенсивность линий в участке, получим

T1 (to) = exp<

XI

I Ti+2X7p J,

- X

t2 = exp< - xe в

J ₀

. x /в j

- iJy

(x)

где X

^^^^»

Sto — я , ^ d

среднее расстояние между линиями.τ 1 = exp (– x ) при 2x<<β.

Если 2x>>β, то

т 1 ® exp ( - Vв x 72 ) ,

^т 2

( exp

V

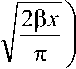
Плассом была рассмотрена случайная модель Эльзассера, в которой полоса поглощения представляется как случайное наложение нескольких полос Эльзассера с параметрами в i = 2 п d i / A i y_t = s_tw /2 п d_t Если A_t -расстояние между спектральными линиями в i -ой полосе Эльзассера, то для этой модели

N да- т=П I 1 i=1  0 L

^-

1 Ae (.yi в i) Pe (Si )dS, A i

где A

i

- эквивалентная ширина линии в i-ой полосе Эльзассера; Pe (Si-) dSi вероятность того, что i-ая полоса Эльзассера имеет интенсивность в пределах от Si до Si- + dSi N - число полос Эльзассера.

В последнее время широкое распространение получила квазистати-стическая модель полосы поглощения. По этой модели весь частотный интервал Δ v , занимаемый полосой, разбивается на более мелкие интервалы 8^ в которых линии располагаются случайным образом и имеют произвольную интенсивность. Линии в данном интервале 8_к группируются на декады по значениям интенсивностей. Пропускание в центре полосы тогда выражается формулой

N

т = П т k(v),(10)

к = 1

^т к = П V I ^{exp [-} S i b ^{( v},^v i ^{) ю dv} ]

>

i ⁵ i 8,-

где k - номер декады; N - число декад; п_к ^Z^iT^ i — число линий в интервале. В расчетах принимается значение N = 5. Квазислучайная модель значительно упрощает расчет, так как в ней функция Q ( S ) заменяется дискретным распределением, различным для различных6_к.

В настоящее время квазислучайная модель полос поглощения используется для получения ФСП почти всех атмосферных газов. Нами рассмотрена точность расчетов ФСП Пласса на примерах полос поглощения паров H₂O и CO₂(для масс до 10 ос. см для паров H₂O и 100000 атм. см для CO₂ ) . Было показано, что ошибки этих вычислений особенно велики при больших содержаниях CO 2 и паров H 2 O и обусловлены неадекватностью представления реальных СП моделью жесткого волчка и контура СЛП – контуром Лоренца. Если параметры СЛП вычислены точно и адекватно учтен контур СЛП, для КВ полос CO₂ и H₂O ошибки вычислений ФСП, как правило, не превосходят 3–5% [75]. Об этом свидетельствуют сопоставления расчетных ФСП по МЧИ тонкой структуры спектров и ММПС, представленные в работах.

Выполненные в ранних работах расчеты спектральной прозрачности имеют одну общую черту – пропускание среды определяется функцией произведения поглощающей массы на давление т = t(wP) . Как показано в [8]–[12], [30]–[35], это допущение справедливо лишь в редких случаях и является одним из источников ошибок расчетов ФСП. Допущение т = t(wP) противоречит не только данным о спектральном поглощении радиации атмосферными газами, но и данным по интегральному поглощению [33].

Au = J (1- тAv )dv , (12)

из этого следует, что при давлениях Р< 1 атм А_и = А_и(щР^2ки) , где к_и <0,5.

Нами рассмотрена возможность использования соотношения т = exp

- A ю

V1 - D ю / p ^{2 k}

для описания ФСП паров H2O, CO2, N2O, CO в узких спектральных интервалах A = 5-20 см-1. Было показано, что в области ^С [0,96-0,05] при давлении Рэ < 1 атм экспериментальные данные по пропусканию можно описать формулой т дV = exp - в„ (юPvmv m v

являющейся предельной аппроксимацией соотношения (13). Параметры P_v, m_v , n_v для большинства активных в поглощении компонентов земной атмосферы и продуктов сгорания органических топлив (паров H₂O, CO₂,

N 2 O, CO, NO, NH 3 , HNO 3 , O 3 , O 2 , N 2 ) в области спектра 0,7–50 мкм были определены и затабулированы в работах авторов с сотрудниками для среднего A = 5-20 см^-1 и низкого A = 0,025-0,1 мкм спектрального разрешения.

Выполненные нами исследования показали, что формула (14) удовлетворительно работает (с погрешностью 5–7 % ) в условиях земной атмосферы, где общее давление Р <  1 атм. Область оптических толщин, в которой поглощениеА д-у пропорционально массе абсорбента, варьирует от 0,01 до 0,04 в зависимости от рода газа и давления. Примеры сравнений ФСП с экспериментом представлены в работах [24], [70]. Отличия параметров 2к = п/m от единицы обусловлено перекрыванием СЛП. С ростом числа линий, входящих в выбранный интервал, их перекрывание увеличивается и параметр 2 k уменьшается. Сказываются на величине этого параметра и соотношения в интенсивностях между сильными и слабыми СЛП.

Применимость соотношения (14) для вычисления ФСП при давлениях

Р >  1атм весьма ограничена, так как с ростом давления вращательная структура полос поглощения «смазывается». Это приводит к увеличению параметра m и уменьшению параметра n. В условиях «смазанной» вращательной структуры m=1, n=0.