Метод модуляции речевого сигнала и его применение в системах речевой обработки
Автор: Калимолдаев Максат Нурадилович, Мусабаев Рустам Рафикович Рустам Рафикович, Мамырбаев Оркен Жумажанович
Журнал: Проблемы информатики @problem-info
Рубрика: Средства и системы обработки и анализа данных
Статья в выпуске: 1 (13), 2012 года.
Бесплатный доступ
Рассмотрен метод модуляции речевого сигнала по амплитуде, предназначенный для модификации интонационных характеристик речевого сигнала
Синтез речи, клонирование речи, речевой сигнал, интонация, просодия, преобразование текста в речь
Короткий адрес: https://sciup.org/14320113
IDR: 14320113 | УДК: 519.7
Текст научной статьи Метод модуляции речевого сигнала и его применение в системах речевой обработки
Введение. Существует задача синтеза речевого сигнала с изменяющейся интонацией. Данная задача наиболее часто решается в рамках систем речевого синтеза по тексту, когда на вход системы подается произвольная текстовая информация, а на выходе получается соответствующий речевой сигнал, максимально приближенный к естественной человеческой речи. Также существует ряд задач по клонированию речевого сигнала, при решении которых синтезируемому качественному речевому сигналу придается максимальное сходство с персональными характеристиками речи [1]. Данная технология является технологией двойного назначения.
Среди работ по данной теме следует отметить работы [1–7] и др.
Предлагаемый метод. В случае компилятивного синтеза речи в системе имеется конечное множество базовых фрагментов речевого сигнала F = {f 1 , f 2 ,..., f n } , где n — общее количество фрагментов. Данные фрагменты получаются в процессе записи речи диктора и последующего автоматического либо неавтоматического выделения их специалистами по фонетике [8]. Размерность базовых фрагментов и их количество зависят от выбранного подхода. Наиболее часто используются речевые фрагменты следующих размерностей:
-
1) полуфон — половина фонемы;
-
2) фонема — целая элементарная единица;
-
3) дифон — два смежных полуфона различных фонем и переходная область между ними;
-
4) слоги, слова, фразы и т. д.
Общее количество выделенных звуковых фрагментов в системе может колебаться от нескольких сотен до нескольких десятков тысяч. Для повышения качества синтеза необходимо увеличивать количество используемых базовых фрагментов, что приводит к увеличению используемых ресурсов, а также времени синтеза.
В компилятивной системе речевого синтеза одновременно используются различные типы базовых фрагментов, составляющие конечное множество T = {t 1 , t 2 , ...,t n } , где n — общее количество используемых типов. Например, можно выделить следующие типы базовых фрагментов T = {V, N, E,P} : V — вокализированные, N — шумовые, E — взрывные и
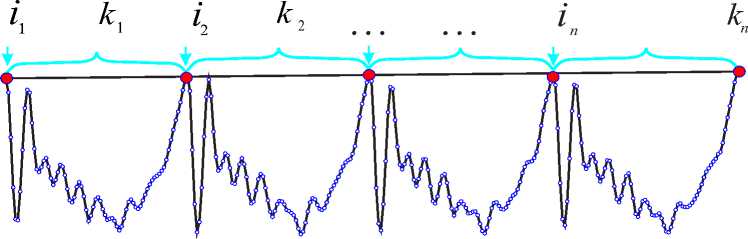
Рис. 1. Исходное сегментированное множество выборок речевого сигнала
щелкающие, P — паузы. Каждому данному типу соответствует множество звуковых фрагментов.
Для каждого типа базовых фрагментов устанавливается набор правил модификации его интонационных характеристик R = {г 1, г2,..., rn}, а также множество методов модификации M = {т 1 (p 11 ,p 12 ,...,p 1 k), m 2 (p 21 ,p 22 ,...,p 21),...,mn (Pn 1, Pn 2,..., Pnj)}, которые используются на основании данных правил. Каждое правило оперирует одним либо несколькими методами с заданным набором параметров {p 11, p 12, ...,p 1 k}. Правила оперируют также множеством характеристик C = { {сB,cB,...,cB^ , {cE,cE,...,cE} } как самого базового фрагмента cB, так и его контекстного окружения ckE . Различным комбинациям данных характеристик могут быть поставлены в соответствие различные методы интонационной модификации. В об-
щем случае при реализации системы синтеза речи по компилятивному принципу необходи- мо оперировать комплексным множеством
X = ( {F 1 , T 1 , R 1 ,M 1 , C 1 } , {F 2 ,T 2 , R 2 , M 2 , C 2 } ,...,
{F n ,T n ,R n ,M n ,C n } ).
Как известно, модулирование интонации производится путем изменения длительностей и частотных характеристик различных фрагментов речевого сигнала, в основном фонем, а также расстановки пауз между фонемами [1]. В речевом сигнале наибольшую интонационную составляющую имеют вокализированные участки, что обусловливает особую значимость регулирования их длительностей и частотных характеристик. Для таких типов речевых фрагментов, как шумовые участки и паузы, без ущерба для качества синтеза можно ограничиться регулированием лишь их длительностей. Таким образом, для осуществления качественного синтеза необходимо использовать набор методов модификации следующих параметров речевого сигнала:
-
— контура частоты основного тона [9];
-
— длительностей фонем [10];
-
— амплитудной огибающей.
В настоящей работе предлагается подход для осуществления модификации амплитудной огибающей вокализированных составляющих речевого сигнала. Данный подход был апробирован и применяется в одной из систем синтеза и клонирования речи [11]. Для того чтобы использовать этот метод, предварительно необходимо выполнить разметку речевого сигнала по частоте основного тона F 0 для элементов множества F Е V .В результате получаем множество сегментов S = (( i 1 , к 1 ) , ( i 2 ,k 2 ) ,..., ( i n ,k n )), которые задаются индексом начальной выборки i n и количеством входящих выборок k n (рис. 1).
После разметки производится нормализация множества сегментов S по амплитуде, для этого используются индексы граничных выборок нормализируемого микросегмента i n и i n +1 . Форма сигнала изменяется таким образом, чтобы выборка с индексом i n +1 была выровнена
+100 %
z s
Z n
7 S
^ n + 1
A
B
In h,
h n +1
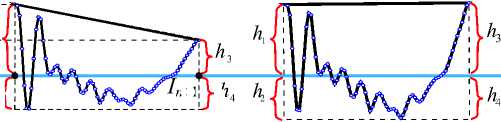
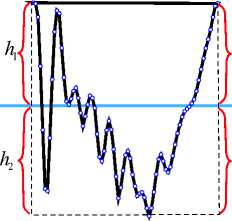
Рис. 2. Процесс нормализации вокализированного микросегмента речевого сигнала по амплитудному уровню:
A — исходный микросегмент, B — нормализация граничных уровней, C — приведение общего уровня к заданному
-100 %
C
L
h 3
t h4
^^^^^^^B
L
до уровня выборки i n . Новое значение амплитудного уровня Z x для каждой выборки с индексом i x E [ i n , i n +1 ] вычисляется следующим образом:
Z x = Z x
1 + x------ in +1 —
H
n
Z n
Z n +1
-
Здесь Z x — дискретное значение речевого сигнала (выборки) при импульсно-кодовой модуляции, при этом мгновенное значение аналогового сигнала измеряется через равные промежутки времени; x E [0 , i n +1 — i n ]; Z n , Z n +1 — соответственно значения дискретных выборок сигнала с индексами i n и i n +1 , i n +1 — i n > 0, Z n +1 = 0. Затем граничные выборки приводятся к заданному амплитудному уровню L , а промежуточные также пропорционально увеличиваются:
Z x =
Z xZL n , Z n = 0,
Z x , " Z n = 0 .
На рис. 2 представлен процесс нормализации сигнала по амплитудному уровню, в результате которого h 1 = |h 2 | = h 3 = |h 4 1 = L . Амплитудная нормализация сигнала позволяет впоследствии применить к нему произвольную огибающую амплитудного уровня и таким образом произвести модуляцию сигнала по громкости. Для задания плавных огибающих используются параметрические кривые Безье [12]. С помощью кривой Безье можно аппроксимировать сложные непрерывные формы колебаний, задав лишь несколько опорных (характерных) точек, через которые должна пройти данная кривая. При увеличении сложности форм аппроксимируемых колебаний достаточно увеличивать количество опорных точек. Кривая Безье задается выражением
n
B (t ) = X Pibi,n (t), 0 где Pi — функция компонент векторов для опорных точек; bin (t) — базисные функции кривой Безье (полиномы Бернштейна): b-п(t>=(n><1 -t>-i- (n)= n — степень полинома; i — порядковый номер опорной точки. С помощью параметра t определяется точка, принадлежащая кривой. При этом за единицу принимается протяженность всей кривой от начальной точки до конечной. Координаты (X, Y) произвольной точки, заданной параметром 0 X = TAX+1 + (1 - T) AX + 6 [ f (T) XPi + f (1 - T) XP] , Y = TAY+1 + (1 - T) AY + 6 [ f (T) Yi+1 + f (1 - T) YP] . Здесь i — индекс ближайшей слева опорной точки из множества A(X,Y ), соответствующей условиям г/Nmax < t и (г + 1) /Nmax > t; Nmax — длина множества A(X,Y) минус единица; AiX, AiY — соответственно i-е элементы множества A(X,Y ), задающие координаты X и Y i-й опорной точки параметрической кривой; f (x) = x3 - x, T = Nmax (t - Dmax Nmax , Dmax tNmax - 1 при tNmax > 0, trunc (tNmax) = 0, trunc (tNmax) , иначе, trunc (x) — функция округления дробного числа до целой части в меньшую сторону. Перед непосредственным вычислением координат (X, Y) произвольной точки кривой проводится расчет следующих значений при изменении г в диапазоне [Nmax- 1, 1]: XP = D (WX - X‘+1 > • YP = D (WY - X+P . Здесь XP = 0; Y0P = 0; XNmax= 0; YPmax= 0. Значения величин W X, WY, Di вычисляются последовательно при изменении г в диапазоне [1, Nmax- 2]: WX = WX1 - 4 WX • WY = W+1 - 4 WY • Di+1 = Di+1- 4. При этом их начальные значения задаются при изменении г в диапазоне [1, Nmax- 1]: WX = 6 ((AX+1 - AX) - (AX - AX-1)) • WY = 6 ((AY+1 - AY) - (AY - AY-1)) • Di = 4. Множества XP , Y P, WY , WX, D имеют размерность, равную размерности множества A(X,Y). Таким образом, имея множество нормализированных дискретных выборок речевого сигнала Z = {zо, z 1,..., zn- 1}, где n — количество выборок, а также функцию Безье Bz (A(X,Y), t), которая задается множеством опорных точекA(XY) = { (A X ,A Y) ,(A X ,A Y) ,...,№ ,AYm)}, где m — количество опорных точек, можно осуществить амплитудную модуляцию сигнала, представленного множеством Z : ERO AY1 L +50 % -50 % Рис. 3. Процесс модификации амплитуды исходного речевого сигнала по огибающей, заданной набором параметрических кривых Безье Результаты оценки трудоемкости и разборчивости методов амплитудной модуляции Метод Трудоемкость Pазборчивость, % Модуляция кривой Безье 12 503 93 Умножение сигнала на коэффициент 1000 87 Zi = ZiBz (A(X,Y), t) , t = —^- (у—I1- + N1) . L — 1 V 2 —11 / Здесь L — общее количество опорных точек; 11 Е [0, n — 1], 12 E [0, n — 1] — индексы дискретных выборок, соответствующие ближайшей левой и правой опорным точкам для выборки zi; N1 E [0; Nmax] — номер ближайшей слева опорной точки для выборки zi. На рис. 3 представлен процесс модификации амплитуды исходного речевого сигнала по огибающей, заданной набором параметрических кривых Безье. Для каждой фонемы (L, AY, N, ER) задается собственная амплитудная огибающая. При этом комплексная огибающая плавно задается общим множеством огибающих каждой фонемы. В приведенном примере AL = {(0;0) (0,6; 0,1) (1;0,2)} I AAY = {(0;0,2)(0, 5;0,35) (1;0,2)} AN = {(0;0) (0,5;0,1) (1;0,2)} [ AER = {(0;0)(0,5;0,21) (1;0)} Заключение. У предлагаемого метода имеются аналоги. Наиболее часто в компилятивных системах синтеза и клонирования речи установка амплитуд фонем осуществляется за счет усиления (ослабления) сигналов фонем путем умножения всех значений сигнала на единый коэффициент, задаваемый энергетическим портретом [1]. В ходе проведенного сравнительного анализа методов получены результаты, представленные в таблице. Трудоемкость метода оценивалась как количество элементарных операций на языке высокого уровня, затрачиваемых на обработку 500 дискретных выборок сигнала. Разборчивость результатов синтеза оценивалась по методике, предложенной ГОСТ Р 50840-95 [13]. Синтез осуществлялся с помощью одного синтезатора, но с использованием различных методов амплитудной модуляции. Результаты проведенных оценок показывают, что с использованием предложенного метода можно добиться большей разборчивости синтезированного сигнала. При этом затраты вычислительных ресурсов также значительно увеличиваются.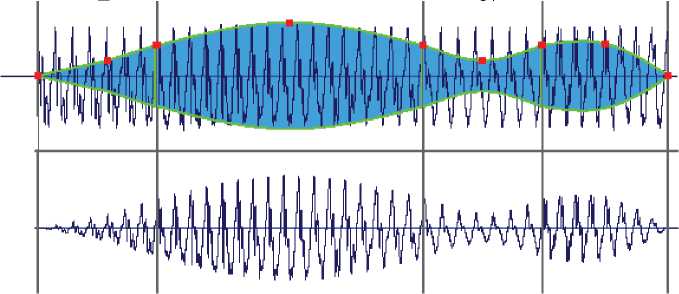
Список литературы Метод модуляции речевого сигнала и его применение в системах речевой обработки
- Лобанов Б.М. Компьютерный синтез и клонирование речи/Б.М.Лобанов, Л.И. Цирульник. Минск: Белорус. наука, 2008.
- Fant G. Speech a coustics and phonetics. Dordrecht: Kluwer Acad. Publ., 2004.
- Фланаган Дж. Анализ, синтез и восприятие речи. М.: Связь, 1968.
- Furui S. Digital speech processing, synthesis, and recognition. N. Y.: Marcel DekkerInc., 2001.
- Taylor P. Text to speech synthesis. Cambridge: Univ. of Cambridge, 2007.
- Xuedong Huang. Spoken language processing: A guide to theory, algorithm and system development/Xuedong Huang, Alex Acero, Hsiao-Wuen Hon. New Jersey: Prentice Hall, 2001.
- Сапожков М. А. Речевой сигнал в кибернетике и связи. М.: Связь издат, 1968.
- Амиргалиев Е. Н., Мусабаев Р. Р. Алгоритмы выделения и классификации фонем в системах синтеза искусственной речи//Пробл. автоматики и управления (Бишкек). 2008. С. 32-35.
- Амиргалиев Е. Н., Мусабаев Р. Р. Определение структуры и способов модификации множества эталонных речевых сигналов в системах синтеза речи//Вестн. КазНТУ. 2008. С.25-28.
- Мусабаев Р. Р. Технологические особенности модуляции продолжительности речевого сигнала в системах синтеза речи//Тр. Междунар. науч.-практ. конф. "Современные проблемы математики, информатики и управления", Алма-Ата, 5 нояб. 2008 г. Алма-Ата: Эверо, 2008. C.98-100.
- Амиргалиев Е. Н., Мусабаев Р. Р. Вопросы разработки информационной системы синтеза и распознавания казахской речи//Вестн. КазНТУ. 2008. № 6. С. 28-34.
- Мусабаев Р. Р. Использование сплайнов при решении задач генерации речевого сигнала//Вестн. КазНТУ. 2008. № 4. С. 173-175.
- ГОСТР 50840-95. Передача речи по трактам связи. Методы оценки качества, разборчивости и узнаваемости. Введ. 21.11.95. М.: Госстандарт России, 1995. 229 с.


