Метод наименьших квадратов в задаче, не имеющей решения

Во всякой науке ощутима потребность прогнозировать те или иные события, но это затруднительно, ведь мы живём в недетерминированном мире, где многое зависит от стохастических, то есть случайных явлений, таких как вспышки на солнце, демографические скачки, или изменения котировок на нефтегазовом рынке. Будь то прогноз курса валют или прогноз погоды – вопрос точности измерений и надёжности полученных данных по-прежнему остается одной из ключевых проблем математики.

Многие процессы – социальные и природные – подчиняются закону причинноследственной связи. Зная характер этой связи, можно построить её математическую модель, и – помещая в неё независимые количественные переменные (такие как время или Лондонская межбанковская ставка предложения) – получить прогноз для интересующей величины: от расстояния смещения литосферных плит до прироста ВВП.

Но невозможно построить прогноз, не располагая данными, иллюстрирующими характер существования исследуемой системы. Самый лучший способ узнать будущее – заглянуть в прошлое. Ссылаясь на закон больших чисел, можно утверждать, что при стремлении количества наблюдений к бесконечности, имея в распоряжении данные о динамике изменения некоторой результирующей величины в зависимости от регрессора (независимой переменной, влияющей на результирующую величину), можно предположить, что эта динамика сохранится в исходном виде. А значит, выбрав интересующий нас регрессор, удастся определить, как поведёт себя результирующая величина при условии, что есть основания предполагать наличие корреляции между этими двумя величинами.

Допустим, в серии экспериментов были получены данные о зависимости двух количественных показателей, где Y – результирующая величина, поведение которой необходимо спрогнозировать, а Х – независимая переменная (регрессор), определяющая Y. Пример динамики представлен в таблице 1.

Таблица 1. Динамика регрессора X и результирующей переменной Y

i	1	2	3	4	5	6	7	8
y i	2	3	4	5	6	7	9	12
xi	7	10	6	17	14	12	18	20

Для наглядности представим имеющиеся данные графически: изобразим корреляционное поле, на котором виден двумер- ный массив данных, где каждому значению X соответствует значение Y (рис. 1).

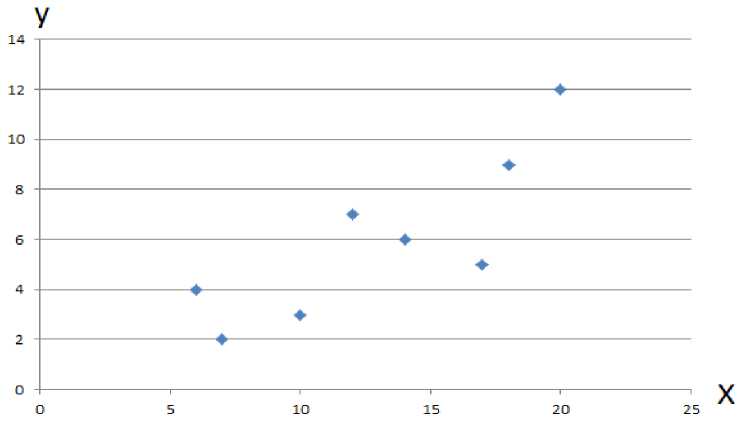
Рис. 1. Корреляционное поле регрессора X и результирующей переменной Y

Явно прослеживается некоторая корреляция и, если судить по виду облака точек, есть основания полагать, что данные находятся в прямой линейной зависимости. Это значит, что увеличение независимой переменной X влечёт за собой и увеличение результирующего показателя Y.

Так как мы наблюдаем рассеяние точек, то нельзя абсолютно точно сказать, как именно поведёт себя исследуемая система в дальнейшем. Но поскольку мы исходим из предпосылки о том, что характер взаимосвязи останется неизменным, для выявления причинно-следственного закона необходимо через эти точки провести прямую, которая послужит нам иллюстрацией динамики, и если выразить её в виде аппроксимирующей функции (аппроксимация – приближение), то она покажет, как именно меняется результирующий показатель в зависимости от регрессора. Такая задача является нерешаемой вследствие первой аксиомы принадлежности: провести такую прямую невозможно.

И, тем не менее, задачу необходимо решить. Следовательно, интересует ответ на другой вопрос: какая прямая наиболее плотно примыкает к этой серии точек? Такую прямую найти можно, а наиболее плотное примыкание означает, что расстояние от значения на искомой прямой до значения на точке должно быть наименьшим. Данное расстояние называется отклонением наблюдаемых значений, а в связи с тем, что имеется не одна точка, а серия точек, задача сводится к следующему: сумма этих отклонений должна быть минимальной.

Поскольку мы предполагаем прямую линейную зависимость, а искомым графиком является прямая, становится очевидным то, что функция также должна быть линейного вида:

y=αx+β.

Коэффициенты α и β являются именно теми условиями, которые диктуют поведение результирующей переменной Y при изменении регрессора X. В тот момент, когда станет известно, каковы значения коэффициентов α и β, задача будет решена. Если бы отклонения отсутствовали вовсе, то значение каждого наблюдаемого случая составило бы:

αxi+β.

Но у нас также есть наблюдаемое значение yi . Значит, отклонение — это разница между предполагаемым значением и наблюдаемым значением в каждой конкретной точке. Соответственно отклонение в точке X составит:

αx i +β-y i .

Именно эти суммарные отклонения для каждой точки X мы хотим минимизировать.

Для достижения поставленной цели можно просто суммировать все отклонения, после чего подобрать коэффициенты α и β таким образом, чтобы получившаяся сумма была минимальной. Проблема таится в том, что отклонение идёт в двух направлениях, вследствие чего может быть как положительным, так и отрицательным.

Во избежание взаимного уничтожения полученных значений и их обнуления, можно использовать метод наименьших модулей, так как по определению модуль – это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Это поможет нивелировать разницу в знаках, но сложность такой вычислительной процедуры высока, а выходные данные могут быть неверно интерпретированы. Также недостатком становится равнозначность для метода больших и маленьких отклонений при условии равенства их общей суммы. Поэтому надёжнее ликвидировать возможные отрицательные значения путём возведения отклонений в квадрат, чтобы наблюдаемое значение yi сыграло свою отрицательную роль в каждой точке. Иначе говоря, рассмотрим сумму квадратов отклонений с первого наблюдения i=1 до последнего наблюдения n (в нашем случае n=8) включительно:

∑ⁿ (αx i + β - y i )²

i=1

Теперь вычислим квадраты отклонений для каждого наблюдаемого случая. Для этого в функцию:

αxi+β-yi подставим соответствующие значения yi и xi из таблицы 1, а затем возведём каждый отдельный результат в квадрат и таким образом, получим:

Таблица 2. Квадраты отклонений наблюдаемых значений

i	1	2	3	4
(αx i + β - y i )2	(7α+β-2)2	(10α+β-3)2	(6α+β-4)2	(17α + β- 5)2
i	5	6	7	8
(αx i + β - y i )2	(14α + β- 6)2	(12α+β-7)2	(18α + β-9)2	(20α + β - 12)2

Cсуммируем полученные результаты:

f(α; β) = (7α+β-2)2 + (10α + β - 3)2+(6α + β - 4)2+(17α + β - 5)2+ (14α + β - 6)2+(12α + β - 7)2+(18α + β - 9)2+(20α + β- 12)2.

Возникла функция, которая зависит от двух показателей α и β. Когда же её значение станет минимальным, мы определим именно те коэффициенты α и β, которые требуются для описания искомой прямой, следовательно, нужно оценить скорость изменения данной функции и исследовать её на экстремумы. Для этого вычислим частные производные и найдем стационарные точки, то есть точки, в которых экстремум возможен. Продифференцировав функцию по переменной α, а затем по переменной β и приведя подобные слагаемые, получим:

f α ^′=3076α+208β-1446; f_β^′=208α+16β-96.

Имеются две частые производные. Теперь требуется, чтобы обе обратились в ноль, ведь именно в этом случае первооб- разная функция достигнет экстремума. В связи с этой необходимостью возникает система уравнений:

3076α + 208β - 1446 = 0;

{  208α+16β-96=0.

Решением данной системы является:

α = 0,53226;

β = -0,91935.

Выясняется, что сумма квадратов отклонений будет наименьшей именно при таких коэффициентах уравнения прямой, а значит, наиболее плотно к имеющимся точкам будет прилегать прямая, являющаяся графиком функции прямой линейной зависимости:

y = 0,53226x-0,91935.

Представим эту прямую на корреляционном поле.

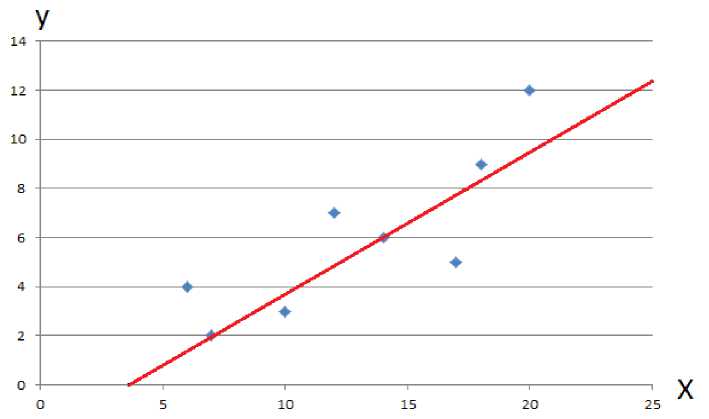
Рис. 2. График функции прямой линейной зависимости

Перед нами наиболее точная иллюстрация зависимости двух величин, которую можно выразить одной прямой: минимизировав суммарное отклонение, удалось максимизировать вероятность того, что в результате нового испытания случайная точка окажется именно на этой прямой или в её окрестностях.

Теперь вернёмся к изначальному вопросу: как спрогнозировать значение переменной Y в дальнейшем при конкретном значении переменной X? Если допустить, что в мире не произойдёт ничего экстраординарного и прогнозируемое событие должно случиться в тех же условиях, в которых собирались экспериментальные данные, достаточно просто подставить в полученную функцию значение регрессора X. Например, при X = 22 получим:

y = 0,53226×22-0,91935 ≈ 10,45.

Таким образом, используя метод наименьших квадратов, можно определить не только будущие значения переменной, но и те значения, которые она принимала ранее при условии, что X – величина, меняющаяся в зависимости от времени или же сама является показателем времени. Отталкиваясь от этой идеи, мы можем рассматривать настоящее состояние Вселенной как следствие его прошлого и причину его будущего. И пусть невозможно подвергнуть анализу все данные о силах, приводящих природу в движение, это и приводит к необходимости искать новые методы решения нерешаемых задач. Возможно, однажды науке удастся найти все ответы, и тогда уже не останется ничего неясного, а будущее – как и прошлое – предстанет настоящим в наших глазах.