Метод наведения 3D-модели объекта на 2D-изображение на основе инвариантных моментов

В задачах распознавания графических образов возникает необходимость манипулирования 3D-моделями объектов для получения проекции, наиболее близкой, в смысле некоторого критерия, к заданному изображению. Пусть заданы пространственная точка М с координатами (ж, у,z) и ее ортогональная проекция т на плоскость наблюдения z = 0 с координатами (ж, у). Под дальностным изображением (range image) будем понимать цифровое изображение, в каждой точке которого яркость /(ж, у) принимает неотрицательные целые значения, равные величине расстояния от точки М до точки т. Предполагается, что дальностное изображение можно преобразовать во множество точек, являющееся 3D-моделью наблюдаемого объекта.

Для корректного сравнения графических образов могут быть применены различные дескрипторы, метрики и методы управления 3D-моделями. Ранее была рассмотрена задача распознавания лиц

с применением инвариантных моментов Hu в качестве признаков для выполнения корректного сравнения 2D-изображений [1] . В настоящей работе предложено расширение этой задачи на трехмерный случай с применением альтернативных инвариантных моментов. Введем некоторые необходимые определения.

Определение 1. Под 3D-изображением понимается кусочно-непрерывная функция /(ж, у, х) трех переменных, определенная на компактном носителе D С R х R х R и имеющая конечный ненулевой интеграл.

Примером подобной функции служит функция яркости /(ж, у, х), которая имеет целочисленные значения при целых (ж, у, х) и хранится в компьютере в виде трехмерного массива. Каждый элемент этого массива представляет собой пиксель с интенсивностью, находящейся в диапазоне от 0 до L — 1. Величина L обычно является степенью двойки (например, 64, 256) и называется глубиной изображения.

Определение 2. Моменты 3D-изображения (image moments) есть отображения кусочно-непрерывной функции /(ж, у, х) в полиномиальный базис — множество многочленов, определенных на компактном носителе D С R х R х R.

Примером служат моменты изображения

^M lm П = У^ P imn f (ж, У, х) dж dy dx,

D где Pimn- полиномиальный базис функций определенных на D; Z, т, п — неотрицательные целые; г = Z + т + п - порядок момента.

Определение 3. Инвариант - функционал I(F ), определенный на изображении F таким образом, что I(F ) = I(D(F )) для пространства всех допустимых преобразований D, в том числе операторов яркостных и аффинных преобразований изображения F .

Для распознавания важно, чтобы I(F 1), I(F 2) были «достаточно различны» для разных изображений F 1, F 2.

Определение 4. Яркостным инвариантом будем называть дескриптор изображения устойчивый к аддитивным и/или мультипликативным изменениям яркости.

Определение 5. Геометрическим инвариантом будем называть дескриптор, который является устойчивым к группе аффинных преобразований изображения.

Рассмотрим задачи сравнения изображений, основанного на применении инвариантных моментов.

1. Сравнение 3D-изображений на основе инвариантных моментов

Пусть f(ж, у, z) есть непрерывная функция, описывающая значение яркости точек с координатами (ж, у, z) в трехмерном пространстве. 3D-моменты определяются путем вычисления следующего интеграла [2] :

« ,„„ — + “       + “

-∞  -∞  -∞

ж¹ y ^т z ⁿ f (ж, у, z) dж dy dz

Моменты всех порядков существуют, если функция f(ж, у, z) кусочно-непрерывна и ограничена в конечной области в 3D-Евклидовом пространстве. Центральные моменты вычисляются следующим образом:

Щтп —

+ ∞   + ∞   + ∞

∞ -∞ -∞

(ж - ж), (у — у) ^т , (z

— z^f (ж, у, z) dж dy dz.

Для дискретного случая (цифрового изображения), который имеет место в нашем случае:

plmn — ЕЕЕ(ж — ^ (у — y)m(z — z)-f (ж,y,z), X Y Z где X,Y, Z - область определения координат точек (пикселей) изображения; (ж, у, z) - геометрический центр 3D-объекта.

Для решения задач распознавания требуется построить моменты, инвариантные к операциям поворота, сдвига и масштабирования. Исходя из практической целесообразности, ограничимся в дальнейшем 3В-моментами с порядком г 6 3. В соответствии с проведенным

Таблица 1. Чувствительность 3D-инвариантов

Момент           I1  I2  I3  F1  F2  F3  F4  F5

Чувствительность  5 2   5 4   5 6   5 6    5 4    5 6    5 6    5 6

поиском из различных источников [2 –4] были выбраны следующие моменты:

1 1 =№ 200 ⁺ № 020 ⁺ № 002 ;

^ 2 =№ 200 № 020 ⁺ № 200 № 002 ⁺ № 020 № 002 - № 101 - № 110 - № 011

^ 3 =№ 200 ^№ 020 ^№ 002 - Р-002 № 110 - ^№ 020 № 101 - № 200 ^№ 011

^{+ 2}№ 110 № 101 № 011 - № 011 - № 101

^F 1 = ^№ 003 ⁺ 6 ^№ 012 ⁺ 6 ^№ 021 ⁺ 6 ^№ 030 ⁺ 6 ^№ 102 ^{+ 15 №} 111 - 3 ^№ 102 ^№ 120

⁺ 6№ 12₀ - ³№ 021 № 201 ⁺ б№ 2₀₁ - ³№ 003 ⁽№ 021 ⁺ № 201 ) - ³№ 030 № 210

⁺ 6 ^№ 210 - 3 ^№ 012 ^{( №} 030 ^{+ №} 210 ) - 3 ^№ 102 ^№ 300 - 3 ^№ 120 ^№ 300 ^{+ №} 300 ;

^F 2 =№ 200 ⁺ № 2)20 ^{+ №} 002 ⁺ 2 ^№ 110 ⁺ 2 ^№ 101 ⁺ 2 ^№ 011 ;

^ 3 = ^№ 300 ⁺ 3 ^№ 200 ^№ 110 ⁺ 3 ^№ 200 ^№ 101 ⁺ 3 ^№ 110 ⁺ 3 ^№ 101 ^№ 020 ⁺ 3 ^№ 101 ^№ 002

• ⁺    № 020 ^{+ 3}№ 020 № 011 ^{+ 3}№ 011 № 002 ⁺ № 002 ^{+ 6}№ 110 № 101 № 011 ;

F 4 =№ 300 ⁺ № 030 ⁺ № 003 ^{+ 3}№ 210 ^{+ 3}№ 201 ^{+ 3}№ 120

• ⁺    3 ^№ 102 ⁺ 3 ^№ 0и ⁺ 3 ^№ 012 ^{+ б №} 111 ^;

F 5 =№ 3₀₀ ^{+ 2}№ 300 № 120 ^{+ 2}№ 300 № 102 ⁺ 2№ 210 № 030 ⁺ 2№ 210 № 030

• ⁺    2№ 201 № 003 ⁺ № 030 ^{+ 2}№ 030 № 012 ⁺ 2№ 021 № 003 ⁺ № 003 ⁺ № 210

• ⁺    2№ 210 № 012 ⁺ 2№ 201 № 021 ⁺ № 1₂₀ ^{+ 2}№ 120 № 102 ⁺ № 1₀₂ ⁺ № 021 ⁺ № 012 .

• 2.    Сравнение 2D-изображений на основе инвариантных моментов

Моменты 1 1 ,..., F 5 являются 3D-HHBapuaHTaMH к операциям поворота и сдвига.

Воздействуя на координаты (ж, у, z) можно установить чувствительность 3D-инвариантов к линейным искажениям изображений. Оценка теоретической чувствительности 3D-инвариантов к геометрическим искажениям с коэффициентом 5 представлена в таблице 1 .

Для получения инвариантов к масштабированию достаточно положить: 5 = ^№200 + №020 + №002 и выполнить нормирование путем деления моментов 11,..., F5 на соответствующие значения коэффициентов таблице 1. Нормированные моменты 11,..., F5 являются 3D-инвариантами к операциям поворота, сдвига и масштабирования. Свойства инвариантности можно проверить путем непосредственной подстановки в выражения для моментов формул аффинных преобразований координат изображения и приведения результата к исходному виду.

Для сравнения 3D-изображений при одинаковых условиях освещенности можно применять их 3D-инварианты и построенные на них метрики, например расстояние Евклида.

Полагая п = 0 в формулах для 3D-инвариантов, получим 2D-инварианты (M 1 , ..., M g ) изображения для плоскости XOY :

^М 1 =Р 20 ⁺ Р 02 ⁺ Р 00 ;

^M 2 =Р 20 Р 02 ⁺ Р 20 Р 00 ⁺ Р 02 Р 00 ^— Р 10 ^— Р 11 ^— р 01 ;

^M 3 =Р 20 Р 02 Р 00 ^— Р 00 Р 11 ^— Р 02 Р 10 ^— Р 20Р01 ⁺ 2Р 11 Р 10 Р 01 ^— р 01 ^— Р 10 ;

^М 4 = ^р 00 ^{+ 6 р} 01 ⁺ 6^ 22 + 6д 0з + 6д 1о + 15^ 11 ^— Зд 1о Д 12 + 6д 12

• ^{—    3}Р 02 Р 20 ^{+ 6}д 2о ^{— 3}Р 00 ⁽Р 02 ⁺ Р 20 ) ^{— 3}Р 03 Р 21 ^{+ 6}м 21

• ^{—    3}Д 01 ⁽Д 03 ⁺ Д 21 ) ^— 3^ 10 ^ 30-- 3^ 12 ^ 30 ⁺ Д зо 5

^M 5 =^ 20 ⁺ М 02 ⁺ Р-00 ⁺ 2^ 11 ^{+ 2}М 1₀ ⁺ 2д 01 ;

^М 6 =Р 20 ^{3 + 3}Р 20 Р 11 ^{+ 3}Р 20 Р 10 ^{+ 3}Р 11 ^{+ 3}Р 102 Р 02 ^{+ 3}Р 102 Р 00 ⁺ р 0 ₂

• ^{+    3}Р 02 Р 01 ^{+ 3}Р 01 Р 00 ⁺ Р 00 ^{3 +} 6Р 11 Р 10 Р 01 ;

^М 7 =^р 30 ^{+ р} 03 ^{+ р} 00 ^{+ 3 р} 21 ^{+ 3 р} 20 ^{+ 3 р} 12 ^{+ 3 р} 10 ^{+ 3 р} 02 ^{+ 3 р} 01

• ^{+    6 р} 11 ^;

^М 8 =Р з₀ ⁺ 2Р 30 Р 12 ⁺ 2Р 30 Р 10 ⁺ 2Р 21 Р 03 ⁺ 2Р 21 Р 03 ⁺ 2Р 20 Р 00 ⁺ р 0 ₃

• ⁺    2Р 03 Р 01 ⁺ 2Р 02 Р 00 ⁺ Р-00 ⁺ Р 21 ⁺ 2Р 21 Р 01 ⁺ 2Р 20 Р 02 ⁺ Р 12

• ^{+    2 р} 12 ^р 10 ^{+ р} 10 ^{+ р} 02 ^{+ р} 01 .

• 3.    Задача наведения 3D-модели объекта на 2D-изображение

Полученные моменты (M i ,..., М § ) являются альтернативными по отношению к известным инвариантным моментам Hu [1] . Аналогично можно построить инварианты для плоскостей XO Z , YO Z . Далее можно применить полученные моменты для сравнения проекций 3D-модели с предъявленным изображением.

Пусть f _m = f _m (x,y) — проекция модели трехмерного объекта на плоскость XOY , f = f (х, у) — заданное полутоновое изображение. В качестве расстояния между предъявленным изображением f и проекцией fm будем использовать величину

W (Р ) =

х ЕИ

N 4=2

- М^ ) ² ,

а в качестве параметров управления [5] — углы поворота 3D-модели вокруг осей Р = (р1,р2,р3). Задачу оптимального наведения целесообразно решать методом градиентного спуска Р [ *^к = arg min( W ^[к^ (Р )), где к -номер итерации. Для этого полагаем известными начальные значения углов положения (р 10^] , р 20^] , P^ ). Значения параметров приближения вычисляют по формулам

[k+i]     '■. X к '•       Л [k]       W ^{[ к +1} (Р ) - W ^{[ к} (Р )

р = р + XAP\ , AP« =--W^R)-----, где: W‘k] (Р) = dWdp ('); к = 0.1,... — номер итерации; Ap^k] — шаг к-ой итерации; А — нормирующий коэффициент.

В основе решения задачи лежит гипотеза о монотонности и унимодальности функции W(Р ) по каждому из параметров управления (р1,р2,р3), выполнение которой упрощает практическую реализацию метода. Для получения оптимума в этом случае достаточно последовательно решить задачи оптимизации по каждому из параметров. Расширением подхода служит метод последовательных уступок.

Таблица 2. Значения инвариантных моментов

Момент	Варианты расположения 3D-изображения лица
	1^Р^ ^^^8^		^l^^^"^^^
1 1	1	1	1
1 2	0.22245	0.22245	0.22245
I 3	0.01283	0.01283	0.01283
F 1	6.255e-06	6.255e-06	6.255e-06
F 2	0.55510	0.55510	0.55510
F 3	0.37115	0.37115	0.37115
F 4	5.52475e-06	5.52475e-06	5.52475e-06
F 5	5.03792e-06	5.03792e-06	5.03792e-06

Таблица 3. Экспериментальное исследование 8 как индикатора масштабирования

Коэффициент масштабирования	Значение 5 до масштабирования	Значение 5 после масштабирования	Отношение значений 5
2	10099.4	20198.8	2
3	10099.4	30298.2	3
0.5	10099.4	5049.69	0.5
0.25	10099.4	2524.85	0.25

• 4.    Экспериментальные исследования

Эксперименты были проведены на примере наведения 3D- модели лица на одну из его случайных проекций. В Таблице 2 в качестве примера приведены расчетные значения демонстрирующие инвариантность моментов для трех положений модели 3D- поверхности лица.

В Таблице 3 приведены значения чувствительности инвариантов и коэффициентов масштабирования для выбранной модели 3D-

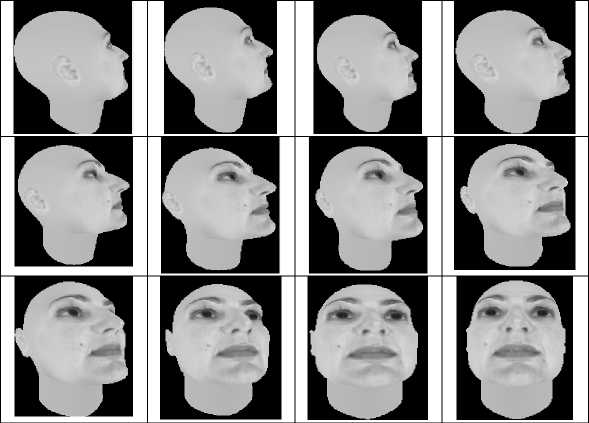
Рис. 1. Последовательность проекций 3d-модели поверхности лица.

Без потери общности рассмотрим однопараметрическую задачу наведения р 1 = argmin(W(р 1 )) путем последовательного вращения 3D-модели вокруг одной оси.

Серия полученных проекций на плоскость XOY в процессе поворота показана на рис. 1 .

Моменты (М 2 ,..., М 8 ) предварительно нормируются в соответствии с таблицей 1 , причем момент М 1 как наименее информативный в дальнейших расчетах не участвует. Характер изменения целевых функций W(р 1 ) и W(р ₂ ) в процессе последовательного поворота модели на Др 1 = 5 и Др 2 = 5 градусов отображен на рис. 2 и рис. 3.

Вид функций говорит об их монотонности и унимодальности по параметрам (р 1 ,р ₂ ), отражающим практически важные для генерации ракурсов изображения повороты вокруг оси OY и OX соответственно, что соответствует выдвинутой гипотезе.

Полагаем, например, что начальное положение 3D-модели, определяется как ( р ^ ⁰ = 0, р 20] = 0, р 30] = 0). Исходя из особенностей задачи,

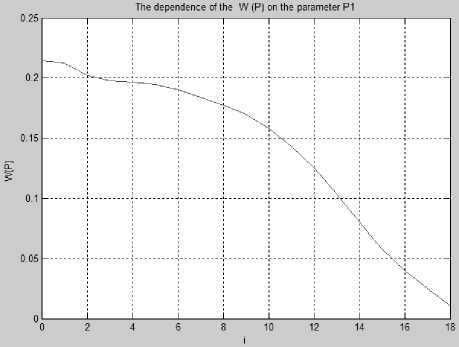
Рис. 2. Зависимость критерия w ( p ) от параметра р 1

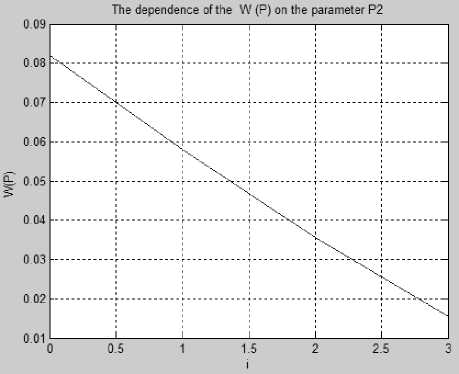
Рис. 3. Зависимость критерия w ( p ) от параметра р ₂

за основу был однопараметрический подход градиентного спуска (для P 1 ). Производные вычислялись с помощью их конечно-разностных представлений W‘_к ](Р) « ^^+7—^-^.

у

Для визуализации этапов наведения был применен простой гра-

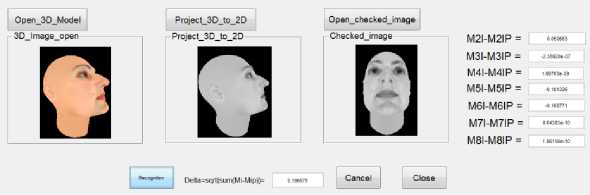
Рис. 4. Графический интерфейс системы наведения и сравнения фический интерфейс (рис. 4), в котором проекция 3D-модели сравнивалась с изображением, представленным справа с применением установленного критерия. Вычисления останавливались, когда значение функции W(Р) по абсолютной величине становилась меньше наперед заданного малого числа е.

Заключение

Представленный метод наведения 3D-модели объекта на 2D- изображение на основе инвариантных моментов имеет несколько преимуществ:

• ( 1 )    становится возможным анализ и распознавание изображений, полученных практически при произвольных ракурсах наблюдения объектов;

• ( 2 )    упрощается сама процедура сравнения изображений (проекции 3D-модели и 2D-изображения), поскольку пространство признаков сжимается до семи, а наличие инвариантов снимает проблему изменения положения изображения в плоскости наблюдения;

• ( 3 )    упрощается в целом процедура наведения за счет учета монотонности и унимодальности целевой функции, выбранной в качестве критерия качества.