Метод нечетких петрофизических композиций при прогнозировании петрофизических параметров
Автор: Кобрунов А.И., Кулешов В.Е., Могутов А.С., Художилова А.Н.
Журнал: Вестник геонаук @vestnik-geo
Статья в выпуске: 9 (201), 2011 года.
Бесплатный доступ
Излагаются результаты прогнозирования проницаемости горных пород с помощью разработанного авторами метода петрофизических композиций, показано преимущество этого метода в сравнении с зарубежным алгоритмом нечеткой кластеризации.
Геолого-геофизические модели, геофизические данные, достоверность, нечеткое моделирование, пористость, проницаемость
Короткий адрес: https://sciup.org/149128535
IDR: 149128535
Текст научной статьи Метод нечетких петрофизических композиций при прогнозировании петрофизических параметров
Построение и анализ взаимосвязей между физико-геологическими параметрами составляет экспериментальный фундамент геофизических методов исследования, подсчета запасов месторождений, прогнозирования и управления технологическими процессами, в том числе процессами контроля за разработкой месторождений углеводородного сырья. Достоверность и надежность этих экспериментально установленных зависимостей составляет основу эффективности всей последующей цепочки геолого-геофизических заключений и прогнозов параметров. Современная практика установления таких связей основана на предположении существования регрессионных зависимостей между изучаемыми параметрами, вид которых и перечень входящих в них параметров постулируется априори. Для нахождения конкретных выражений этих зависимостей и параметров их характеризующих используются в частности приемы статистической обработки данных и, в конечном итоге, осуществляется замена реального экспериментального материала полученными закона- 18
ми, и некоторой интегральной, т. е. общей для всей зависимости в целом, оценкой меры тесноты связи. В соответствии с принятой технологией далее найденный закон в виде уравнений связи между параметрами переносится на изучаемый объект. Этот путь зачастую является источником ошибочных заключений, которые могут привести от неверно выбранных условий вскрытия и режимов эксплуатации скважины до ошибок в точках заложения скважин и в заключениях о запасах и ресурсах углеводородного сырья в регионе. Источники этих ошибок состоят, во-первых, в хорошо известных проблемах, обусловленных переносом связей, полученных в одном районе (территории, скважине, интервале), на другой. А во-вторых, в необходимости при установлении этих зависимостей пользоваться достаточно спорными предположениями. Важнейшее из них состоит в том, что реальные и неизвестные зависимости, если таковые вообще существуют, подменяются некоторыми априорно заданными классами аналитических зависимостей — линейные уравнения, экспоненциаль ные зависимости. Здесь сразу можно выделить как минимум два недостатка. Первый — это априорное постулирование вида принимаемой зависимости. Второй — предположение, заложенное в процессе нахождения параметров конкретной зависимости состоящее в отнесении всего, что не укладывается в эту зависимость к шуму — мусору разной интенсивности, который в лучшем случае может быть лишь оценен. Относительно значимым источником погрешностей при установлении зависимостей в виде уравнений регрессии, служит используемая технология нахождения параметров уравнений, основанная на предположениях о статистическом характере «шума». Например, метод наименьших квадратов для построения уравнения регрессии основан на предположении о нормальном законе вероятностного распределения для этого шума: отличия реальных данных от предполагаемой линии регрессии. Но это искусственное предположение, мало относящееся к природе изучаемых объектов.
В настоящей работе для выполнения процедур прогнозирования в
развитии принципов, заложенных в [1], предлагается рассматривать экспериментальные геолого-геофизические данные и связи между ними, как нечеткие множества и соответственно нечеткие отношения, выполняя на основе цепочки установленных отношений прогноз требуемых параметров, находящихся в конце цепочки. Эту операцию будем называть нечеткой композицией петрофизических отношений, а метод на ней основанный — метод нечетких петрофизических композиций (название вводится впервые). Для установления и оперирования нечеткими отношениями предлагается использовать методы нечеткого моделирования. В такой форме применяемый аппарат прогнозирования параметров, включая подсчетные параметры для запасов углеводородов, адекватен смысловому содержанию и точности исходных данных. Оперирование данными как нечеткими является более объективным. Оно не только позволит избежать ошибочных выводов, связанных с заменой реального материала его выхолощенным аналогом, в виде постулированных аналитических зависимостей, но и дать в конечном итоге реальное представление о мере достоверности выполненных прогнозных заключений и мере возможностей тех либо иных и альтернативных заключений.
Обращение к методам нечеткой алгебры, нечеткой логики и теории нечеткого вывода становится весьма распространенным для геолого-геофизической отрасли. Обоснование этому приведено в [4,
-
5] . Тем не менее применение цепочки нечетких отношений для выполнения завершающего прогноза ранее не проводилось. Методы нечеткого моделирования использовались для решения вспомогательных, подготовительных задач прогноза параметров, не затрагивая традиционные приемы установления регрессионных зависимостей. Одной из наиболее показательных работ в этом отношении служит: «A rule based fuzzy model for the prediction of petrophysical rock parameters» [3] (Принцип, основанный на нечеткой модели, для прогнозирования петрофизических параметров породы) на примере материалов продемонстрируем предлагаемую технологию метода нечетких петрофизических композиций, одновременно выполнив сопоставление получаемых результатов.
Метод нечеткой кластеризации, изложенный в [3] при прогнозировании петрофизических параметров состоит в объединении нечеткого алгоритма кластеризации с методом наименьших квадратов, в результате чего строится кривая проницаемости по зависимостям от плотностной пористости и пористости по керну. Технология нечеткой кластеризации, разработанная авторами Jose Finol, Yi Ke Guo, Xu Dong Jing, включает в себя этапы:
-
1. Нечеткое объединение, т. е. разбиение конечного множества точек данных на число классов (кластеров) с соблюдением меры сходства.
-
2. Настойка функции принадлежности.
-
3. Получение последующих параметров как наименьших квадратов аппроксимации.
-
4. Моделирование пористости от плотности.
-
5. Моделирование проницаемо -сти от пористости.
В результате нечеткая модель определяется множеством нечетких выводов с линейными последовательными частями, каждая из которых устанавливает частные линейные соотношения зависимости ввода-вывода между переменными модели. Эти частные линейные уравнения применяются для расчета прогнозных параметров, результатом чего служат приводимые в работе результаты прогноза проницаемости по измеренной плотности горных пород по стволу скважин Сеутского месторождения в Венесуэле. Эти материалы так же послужили основой для тестирования по алгоритму нечетких петрофизических композиций.
Технология нечетких петрофизических композиций основана на теоретических принципах построения композиции Мамдани и нечетких композиций в целом [5]. Включает в себя следующие этапы:
Фазификация, состоящая в представлении исходных данных в виде нечетких множеств и нечетких переменных.
Установление цепочки нечетких отношений между парами исходных данных.
Расчет композиций нечетких отношений для установления отношений между начальными и конечными параметрами в цепочке (на основе композиции Мамдани).
Продолжение найденной композиции в область задания исходных параметров для прогноза.
Выполнение прогноза промысловых подсчетных углеводородов, параметров как нечетких величин.
Дефазификации установленных нечетких отношений, обеспечивающей переход от нечетких к четким зависимостям с оценкой меры их истинности [1, 5].
Подчеркнем, что ни на каком этапе не устанавливаются какие-ли бо уравнения регрессии между параметрами вообще и линейные зависимости в частности. Вместо этого используются нечеткие отношения, устанавливаемые по экспериментальным данным, служащими формой их выражения.
Для выполнения расчетов создано специализированное программное обеспечение для всех этапов описанной технологии, оперирующее с цепочкой данных, элементы которой обозначаются (X, Y, Z). В частности, X — это данные о пористости, полученные на основе измерений плотности, Y — это данные о пористости, полученные на основе анализа кернового материала, Z — данные о проницаемости пород, полученные на основе анализа кернового материала. Пары значений из массивов X, Y и Y, Z увязаны между собой поскольку относятся к одним и тем же образцам. Задача состоит в прогнозе проницаемости (параметра Z) по измеренным вдоль оси скважины плотности (данные ГГК(п)), пересчитанной в пористость X по геофизическим данным. Заключение о величине параметра z е Z, соответствующего параметру х е X, должно исключать промежуточное явное нахождение у, хотя и неизбежно использовать информацию о связи (X, Y), (Y, Z).
Исходные данные, взятые из работы [3] об экспериментальной взаимосвязи между плотностной пористостью и пористостью по керну, а также между пористостью по керну и проницаемостью для поисковой скважины Сеутского месторождения в Венесуэле, приведены на рис. 1 и 2 соответственно.
Фазификация. Процедуру фазификации данных и установления отношений рассмотрим на примере (X, Y). Для данных (X, Z) или любых других все делается аналогично. Исходные данные X = { х. , i = 1+N}; Y = { yi , i = 1+N} представлены в виде упорядоченных пар значений { х ( i ), y ( I )} и в этом случае они являются нечеткими переменными. Рассматриваем связь X ^ Y. Выберем некоторый интервал А х и разобьем весь диапазон значений параметра X е [ хтш , хтах ] На иНТерваЛЫ xk + А х , k = 1,_K, шириной А х . Сгруппируем значения х ( t ) внутри каждого из них и вычислим среднее значение хк и меру разброса:
-
1 РА
^^^yZ^-^2 , где NX(k ) — число элементов из х ( t ), попавших в интервал с номером k . Для каждого интервала [ xlX(k.+1) ] ставятся в соответствие величины y ( t ), адекватные тем номерам i , которые входят в х ( i ), содержащихся в этом
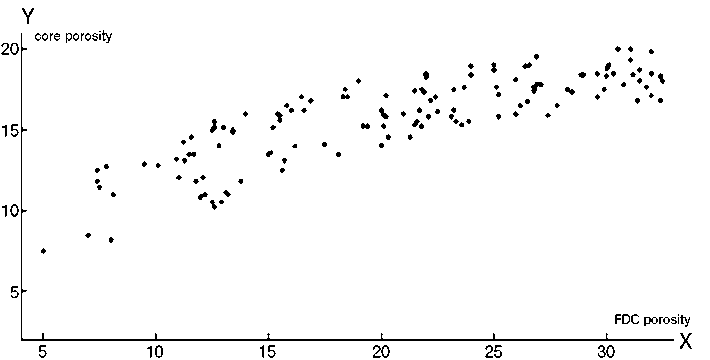
Рис. 1. Зависимость между плотностной пористостью и пористость по керну
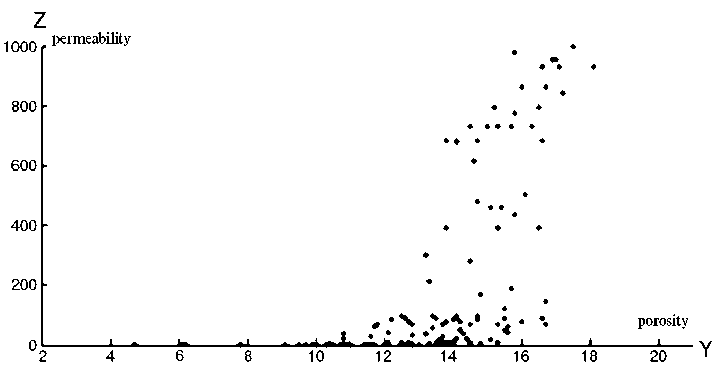
Рис. 2. Зависимость между пористостью по керну и проницаемостью
[x k X (k+1) ] интервале. Они имеют среднее ук и меру разброса
1 Г 11/2
^^у»)^^®-^2 .
Таким образом, принимая экспоненциальную форму представлений для функций принадлежности [1] получим, что переменная X представлена своими K значениями с функцией принадлежности
^^cb^
1 (х - хку \
2 а2(хк) /
характеризующейся параметрами центра хк и разброса о(хк), а переменная Y функцией принадлежности f . 1 / 1(у-Ук)Л
,
<Чук) \ 2 <т2(Ук) ) характеризующейся параметрами центра у к и разброса о(ук). По аналогичной схеме могут быть установлены любые другие функции принадлежности, реализующие фазификацию исходных данных.
Установление нечетких отношений между переменными. Нечеткое отношение между переменными X и Y задаются функцией принадлежности р( у , x ), вычисляемой следующим образом. Для каждого x е X находится номер к , для которого x е [ xk X(k+1) ]. С этим к выбирается ук, таким образом функцией от x : yk( x ). Далее функция принадлежности
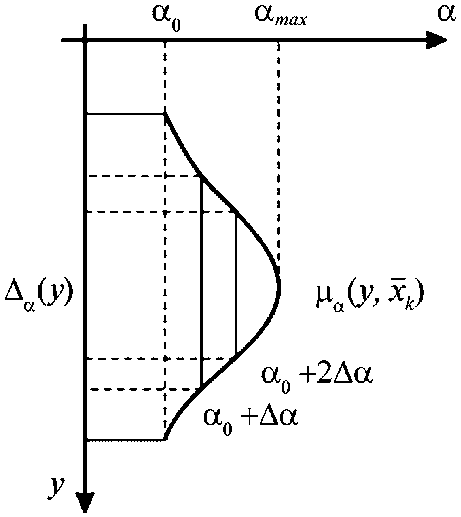
Рис. 3. Интервалы принадлежности
Ц(у.х) =
1 / i (y-y/cto)2 \
O"(ykto)exp\ 2 У2(Ук№) ). Для каждого уровня значимости а от а0 до атах, заданными с некоторым интервалом Да функция принадлежности а = ц(у) характеризуется своими сечениями (рис. 3). Ширина этого интервала Да(у) характеризует интервал принадлежности при прогнозировании значений нечеткой переменной у с качеством а, достоверностью P = Да/Да . Наибольшую достоверность, но низкое качество а0 имеет прогноз интервала Да . Наибольшее качество прогноза, но с нулевой достоверностью для нечетких — не дельтообразных функций принадлежности обеспечивается для прогноза соответствующего максимуму функции принадлежности.
На рис. 4 показана поверхность в трехмерном пространстве как результат фазификации отношения между плотностной пористостью — X и пористостью по керну — Y, соответствующая данным из рис. 1.
На рис. 5 приведена поверхность в трехмерном пространстве как результат фазификации отношения между пористостью по керну — Y и проницаемостью — Z, соответствующая данным приведенным на рис. 2.
Композиция Мамдани как центральный элемент метода нечет-
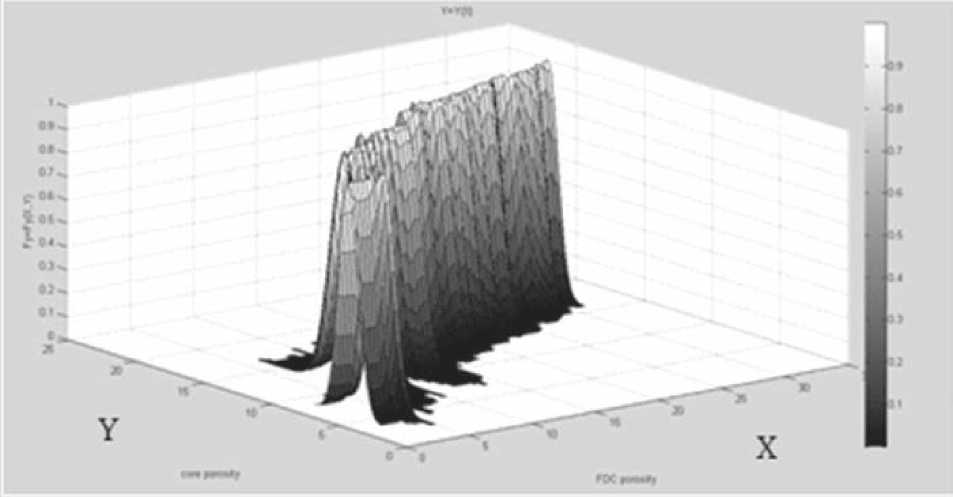
Рис. 4. Результат фазификации отношения между X и Y
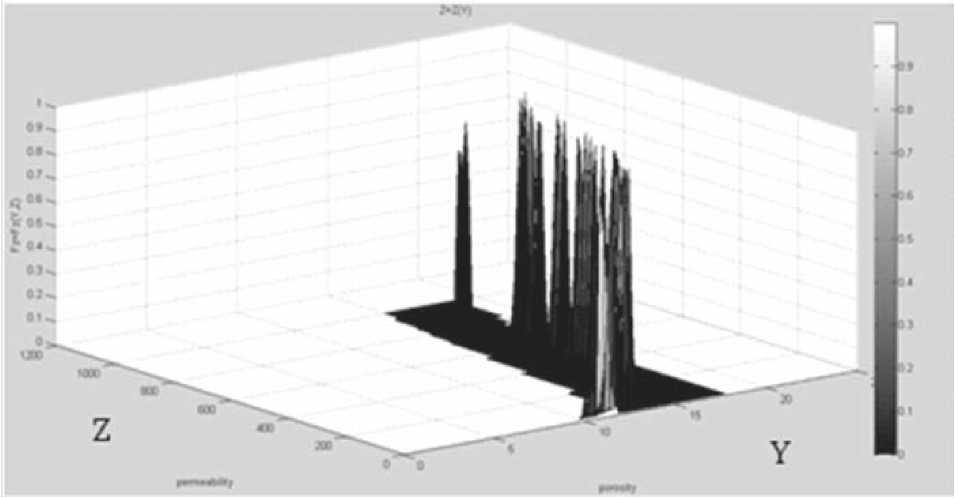
Рис. 5. Результат фазификации отношения между Yи Z
ких петрофизических композиций [1], позволяет установить функцию принадлежности ц( z , x ) для начальной и конечной нечетких переменных — X, Z в выделенной цепочке по установленным функциям принадлежности ц( у , x ) и ц( z , у ). В данном случае это отношение, определяемое функцией принадлежности между плотностной пористостью — X и проницаемостью — Z. На рис. 5 приведена поверхность в трехмерном пространстве как результат найденной композиции, демонстрирующей объективные отношения между плотностной пористостью и проницаемостью.
Таким образом, получено нечеткое соотношение между плотностной пористостью и проницаемостью с исключением промежуточного параметра (пористость по керну). Ось OZ на рис. 6 показывает значение функции принадлежности для пары нечетких переменных (X, Z).
Результаты дефазификации установленных нечетких отношений удобно представлять в виде интервалов принадлежности с соответствующим качеством и достоверностью прогноза. Собственно этим и завершается вычислительная компонента технологии нечетких петрофизических композиций и все дальнейшее сводится к выполнению прогноза по полученным интервалам. Например на рис. 7, а показано, что каждому значению плотностной пористости соответствует интервал принадлежности изменения значения пористости по керну, при этом интервал имеет свои параметры качества и достоверности. Напомним, что интервал — это сечение функции принадлежности по уровню качества а. Достоверность — отношение мер интервала принадлежности, соответствующего уровню а и максимальному интервалу, соответствующему минимальному качеству — сечению.
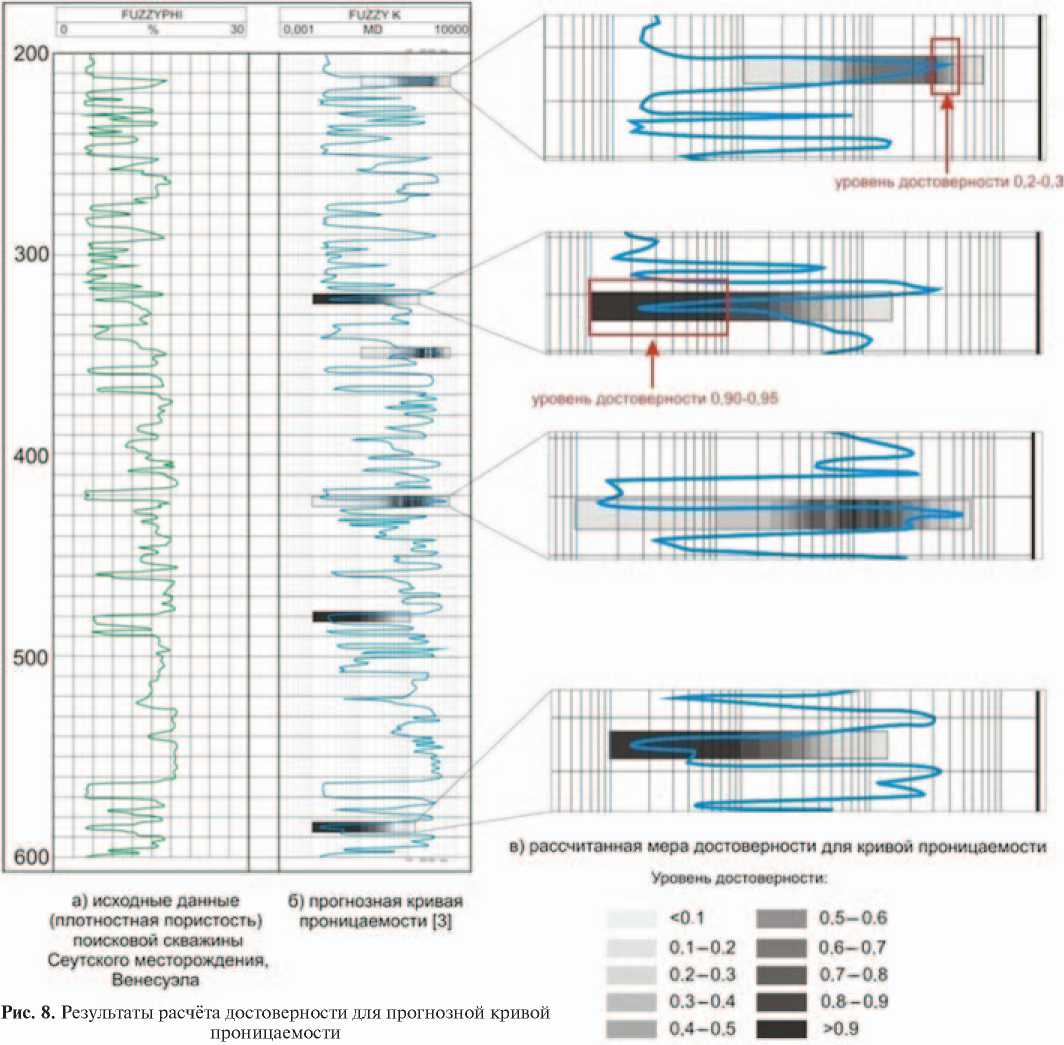
Воспользовавшись диаграммой исходных значений пористости, рассчитанных по геофизическим измерениям вдоль скважины [3] получим, применяя найденные сечения, прогноз, изображенный на рис. 8.
Важно отметить, что вместо значения прогнозного параметра (проницаемости в каждой точке) получается интервал значений с соответствующими взаимообратными достоверностью и качеством. Кроме того, не по всем интервалам исходных данных прогноз допустим, в принципе — нет объективных данных для многих интервалов. Прогноз в этих местах выполняется по данным, которых нет в исходных значениях. Это плод творческого подхода авторов.

Рис. 6. Результат фазификации отношения между X и Z
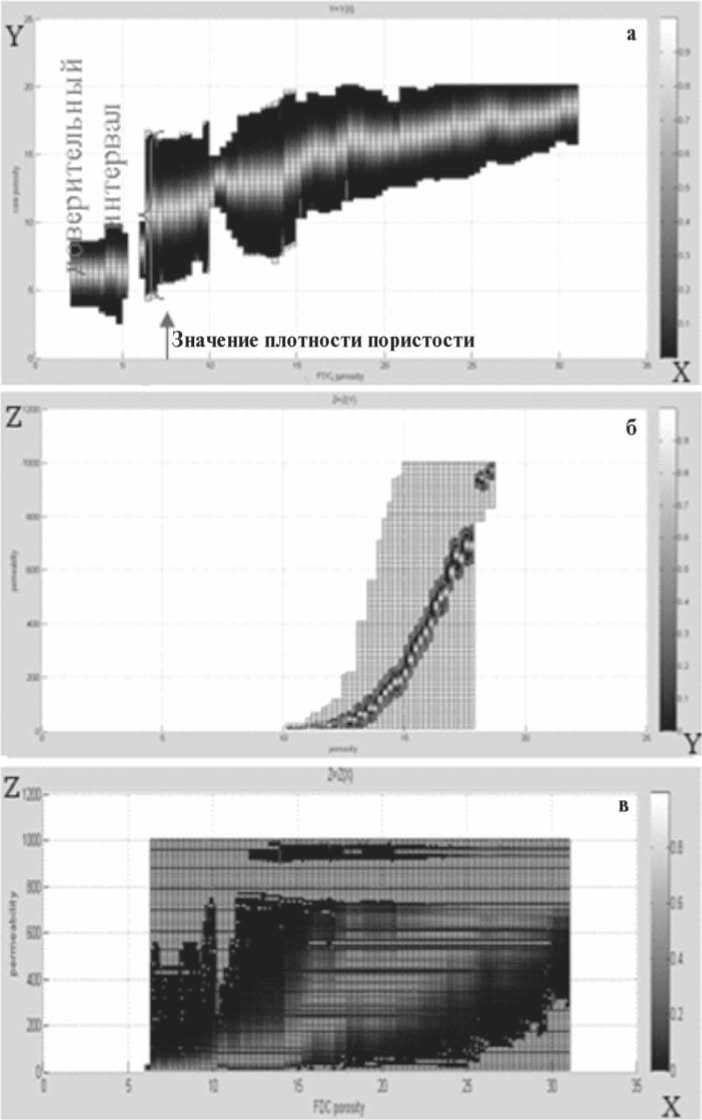
Рис. 7. Уровни сечения функции принадлежности:
а — между плотностной пористостью и керновой пористостью; б — между керновой пористостью и проницаемостью; в — между плотностной пористостью и проницаемостью
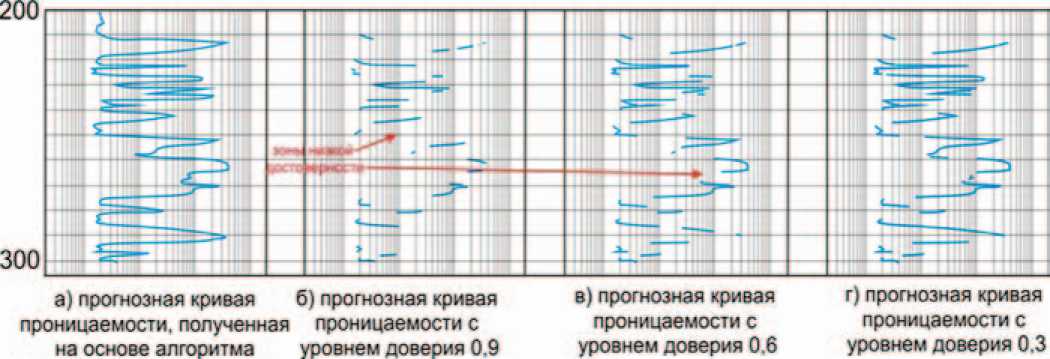
Построенные композиционные отношения отражают объективную информацию и ничего более. Они могут использоваться для оценки качества и достоверности прогноза, выполненного другими методами, в частности метода нечеткой кластеризации [3]. С этой целью следует оценить интервал (сечение) с наибольшим качеством, включающим в себя прогнозное значение. Это качество и соответствующая ему достоверность отражают объективное соответствие экспериментальным данным, которое можно назвать экспериментальной достоверностью выполненного по любой технологии прогноза параметров. Такие оценки результатов прогноза, приведенных в [3], показаны на рис. 8, в. Показано, какие интервалы достоверности имеют характерные точ ки кривой проницаемости, полученной путем объединения нечеткого алгоритма кластеризации с методом наименьших квадратов в работе [3]. Применение этого алгоритма не является эффективным для всей кривой проницаемости. Выделяются немногочисленные участки с достоверностью 0.9. Но в тоже время показаны интервалы с достоверностью 0.2—0.3, что ставит под сомнение возможность применения алгоритма нечеткой кластеризации, который не позволяет оценивать достоверность прогноза, и формирует ошибочные результаты. Также имеются недостоверные зоны, которые необходимо исключить из прогноза. Утверждение об ошибочности результатов подтверждает рис. 9, на котором показана кривая проницаемости с разными уровнями доверия.
Данная кривая имеет уровень доверия 0.9 лишь на немногочисленных и небольших интервалах. Вся прогнозная кривая, полученная с помощью алгоритма нечеткой кластеризации [3] имеет уровень доверия менее 0.3, что является недопустимым в случаях прогнозирования подсчетных параметров и последующих расчетах запасов углеводородного сырья.
Как видно из приведенного примера, вместо получения конкретного значения были получены интервалы доверия, что является более объективным, исходя из имеющейся информации, характеризующейся большой неопределенностью.
Геофизические исследования и полученные по этим данным значения петрофизических параметров являются основой для построе-

нечёткой кластеризации
Оценка уровней доверия по результатам предлагаемой технологии
Рис. 9. Кривая проницаемости из работы [3] с различными уровнями доверия ния трехмерных емкостных и фильтрационных геологических моделей. Описанные выше в работе эксперименты выполнены для единичных кривых по отдельным скважинам. Перспективно развитие технологии многомерного прогноза на основе описанного метода нечетких петрофизических композиций для построения достоверных физико-геологических моделей, построения куба неопределенности при подсчете запасов углеводородов, оценки достоверности и качества выполненных прогнозных построений. Результатом же конечного прогнозирования должна служить пространственно распределенная в некотором кубе мера неопределенности (или ее характеристика), отражающая надежность информации о значениях прогнозируемых параметров в кубе параметров.
Работа выполнена при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009— 2013 гг.».
Список литературы Метод нечетких петрофизических композиций при прогнозировании петрофизических параметров
- Кобрунов А. И., Григорьевых А. В. Методы нечеткого моделирования при изучении взаимосвязей между геофизическими параметрами // Журнал Геофизика, 2010. № 2. С. 17- 23.
- Ампилов Ю. П. От сейсмической интерпретации к моделированию и оценке месторождений нефти и газа. М.: Изд-во «Спектр», 2008. 384 с.
- Jose Finol, Yi Ke Guo, Xu Dong Jing. A rule based fuzzy model for the prediction of petrophysical rock parameters // Journal of Petroleum Science and Engineering, 2001. № 29. P. 97-113.
- Жабреев И. П., Хургин Я. И. Нечеткая математическая модель при подсчете нефти и газа // Геология нефти и газа, 1993. № 11.
- Бочарников В. П. FUZZY - технология: Математические основы. Практика моделирования в экономике. СПб.: Наука РАН, 2001. 328 с.


