Метод Нелдера-Мида решения задачи оптимизации геометрической формы ствола автоматической пушки для улучшения колебательных характеристик

Важной характеристикой автоматических пушек является кучность стрельбы. В работах, посвященных колебаниям ствола, показана значимость влияния начального прогиба и колебаний ствола на точность и кучность стрельбы очередями из автоматической пушки [1-6]. Также из практических исследований известно, что именно прогиб ствола и поперечные колебания оказывают ключевое влияние на точность, при этом крутильными колебаниями можно пренебречь [7]. К основным факторам, вызывающим колебания ствола относят: интенсивный рост Суфиянов Вадим Гарайханович, доктор технических наук, доцент, профессор кафедры «Прикладная математика и информационные технологии».

давления, обусловленный сгоранием порохового заряда; взаимодействие снаряда со стволом, а также технологические отклонения линии центров канала ствола, получаемые в процессе изготовления стволов [8, 9].

Автоматические пушки в значительной степени подвержены влиянию колебательных явлений, поскольку в процессе стрельбы очередями ствол не успевает стабилизироваться и выход снарядов из дульного среза происходит в различные фазы колебаний. Это приводит к появлению отклонений от расчетных значений начальных углов вылета и скоростей снаряда, а также моментов силы, действующей на снаряд, что влияет на точность поражения цели. Колебания стволов зависят от множества факторов: толщины, длины и геометрической формы стволов, свойств материалов, нагружения давлением пороховых газов, интенсивности стрельбы и т.д. В этой связи, актуальной задачей является определение положения, скорости и направления движения снаряда в момент его выхода из дульного среза. Эти значения могут быть получены экспериментально или на основе трехмерного моделирования напря- женно-деформированного состояния ствола и снарядов в процессе выстрела. Экспериментальные исследования требуют значительных затрат на изготовление ствола и его апробацию, основным же недостатком трехмерного моделирования является значительные временные затраты на проведение вычислений. В этой связи, использование верифицированной одномерной математической модели колебаний ствола позволяет значительно уменьшить время расчета [4, 10] и, соответственно, решить задачу оптимизации геометрической формы ствола в приемлемые сроки.

В работе [10] показано, что амплитуда колебаний может быть заметно снижена с помощью применения ребер жесткости, что должно в среднем повысить кучность стрельбы. Однако вопрос об оптимальной форме ствола остается открытым. Целью данной работы является разработка эффективного метода оптимизации геометрической формы ствола для уменьшения амплитуды колебаний и разброса снарядов при стрельбе очередями из автоматической пушки.

1. ОДНОМЕРНАЯ

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОЛЕБАНИЙ СТВОЛА

Рассмотрим математическую модель в виде системы уравнений продольно-поперечных колебаний упругого стержня [11]. Ствол представляет собой трубу длины L с переменным поперечным сечением, ось которого будет совпадать с осью координат Ox . Обозначим площадь поперечного сечения F = F( x ), а площадь канала ствола – S = S( x ). Также предположим, что влиянием поперечных перемещений на продольные можно пренебречь. Запишем уравнение баланса сил, действующих вдоль оси Ox , проходящей через центры поперечных сечений канала ствола [9]:

д ² u . д xx д S

РF-^ = -рFg sin ф- q, + (FG )-p, , (1) д t дx дx где u = u(x,t) – продольные перемещения ствола; p - плотность ствола; g - ускорение силы тяжести; ф - угол возвышения ствола; q 1 = q 1(x,t) – распределенные внешние силы, действующие в продольном направлении по оси Ox, в том числе, связанные с взаимодействием снаряда со стволом; p1 = p1(x, t) – распределение избыточного давления внутри канала ствола:

Р i (x, t ) = P (x, t)- P a, в котором p(x,t) – распределение давление газопороховой смеси, получаемое из решения основной задачи внутренней баллистики, а pа – атмосферное давление; стxx = стxx(x,t) - напряжения, возникающие в продольном направлении, определяемые по формуле:

G xx = E    + V J ( g yy + g _zz df - C E J T ( x , r , t ) df ,(2)

дx  F F              F F где E - Модуль Юнга; v - коэффициент Пуассона; a - коэффициент линейного теплового расширения; T(x,r,t) – температура ствола в точке с координатами x и r в момент времени t.

Второе слагаемое в соотношении (2) для стволов кольцевого сечения определяется из решения задачи Ламе [12]:

• 1    j(a” + G’ df = 2 pi -^Ц , (3)

FF ri- ri где r1 = r1(x) – внутренний радиус ствола; r2 = r2(x) – внешний радиус ствола. В общем случае проводится интегрирование численного решения задачи напряженно-деформированного состояния в поперечных сечениях ствола.

Третье слагаемое в соотношении (2) определяется на основе решения уравнения теплопроводности в квазиодномерной постановке в поперечных сечениях.

Начальные условия для дифференциального уравнения (1) имеют вид:

u ( x, 0 ) = u ₀ ( x ) , l u- = 0 , ^{(4) д} t t = 0

где u ₀( x ) – начальное продольное перемещение, определяемое из решения стационарной задачи о прогибе ствола под действием силы тяжести [10].

Граничное условие закрепления на казенном срезе u (0, t ) = u 0 (o)                 (5)

и условие отсутствия внешних сил на дульном срезе

Z7Z7 д ^M

FE д x

= o .

x = L

Уравнение баланса сил, действующих по оси Oy с учетом технологических отклонений v ₀₀ = v ₀₀( x ) линии центра канала ствола и эффекта Бурдона записывается в виде:

р F |"2" = ^- p Fg ^cos Ф ^- q 2 ^{+ (} F ^G" ⁺ P i S ^{) д (} v ⁺ 2 ^{v 00} ) ⁺ д t                                        д x

+ ^V TT If ( g "^ + G ^zz ) ydf | -!ч f EJ z |^ v 1 -!ч I a E J T ( x , r , t ) ydf д x ^ F               J д x ( д x ) д x I *

с начальными условиями v (x ,o) = vo (x), dv

d t

= 0, t=o

граничными условиями закрепления на казен- ном срезе v (0 ,t ) = v 0 M д v дx

= 0

, x=0

и мягкими граничными условиями, соответствующими отсутствию перерезывающей силы и изгибающего момента, на дульном срезе

EJ — J* dx2

= o, x=L

Л f EJ — ) d x ( z d x ² J

= o, x=L

где v = v ( x,t ) - поперечные перемещения ствола в вертикальной плоскости; v ₀( x ) - величина начального прогиба в вертикальной плоскости; q ₂ = q ₂( x,t ) - распределенные внешние силы, действующие по оси Oy , в том числе, связанные с взаимодействием снаряда со стволом; J z = J z ( x ) -момент инерции сечения относительно оси Oz.

Аналогично (7) записываются уравнение баланса сил, действующих по оси Oz с учетом технологических отклонений w ₀₀ = w ₀₀( x ) линии центра канала ствола:

центром. Внутренние геометрические размеры ствола будем считать неизменными, так как их модификация потребует разработки новых видов боеприпасов и приведет к дополнительным издержкам при производстве. В качестве управляемых переменных для классического ствола выберем внешние диаметры в N + 1 сечениях, как показано на рис. 1. Тогда вектор управляемых переменных для классической формы ствола запишем в виде x = ( D ₀, D 1,..., D N ).

Рис. 1. Продольное сечение ствола с обозначением внешних диаметров на ключевых участках ствола

р F ³-W = - q , + ( F а - + p, S №+^1 + о t                            d x

■ v"^f J (а - + а -) zdf ) -^f EJ y d w 1 -^f a E j T ( x , r , t ) zdf ax² ( F                J ax² ( d x² J ax² | F

с начальными условиями

w ( x, o ) = и ;, ( x ) , ^ w   = o ,       ⁽¹²⁾

^d t t = o

Наряду со стволом классической формы рассмотрим также стволы с ребрами жесткости двух типов [10], представленными на рис. 2.

граничными условиями закрепления на казен-

ном срезе

w ^{( 0} t ) = w ° ^{( o )}

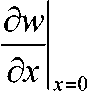
= 0 ,

и граничными условиями на дульном срезе

EJ — ^{J y} d x²

= o, x=L

^ f d w dx I ^y dx²

= o , (14)

x = L

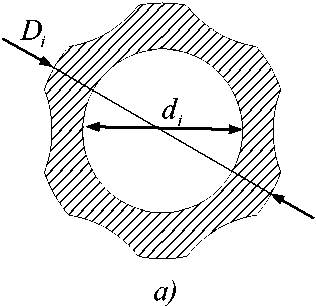
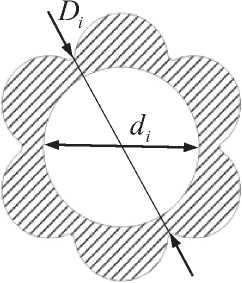
Рис. 2. Поперечные сечения с ребрами жесткости: а) 1-го типа; б) 2-го типа

где w = w ( x, t ) - поперечные перемещения ствола в горизонтальной плоскости; w ₀( x ) - величина начального прогиба в горизонтальной плоскости; q ₃ = q ₃( x,t )- распределенные внешние силы, действующие по оси Oz ; J y = J y ( x ) - момент инерции сечения относительно оси Oy.

Аналитическое решение системы уравнений в частных производных (1), (7) и (11), с соответствующим начальными и граничными условиями вызывает некоторые затруднения, что связано со сложностью этих уравнений и заданием в табличном виде отдельных параметров задачи, таких, например, как геометрия ствола, распределения давления и др. Численное решение краевой задачи продольно-поперечных колебаний ствола было получено на основе разностной аппроксимации представленных выше уравнений интегро-интерполяционным методом [13].

2. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ФОРМЫ СТВОЛА

Рассмотрим классическую (цилиндрическую) форму ствола артиллерийского орудия с кольцевым сечением. Поперечное сечение такого ствола представляет собой область, ограниченную двумя окружностями с совмещенным

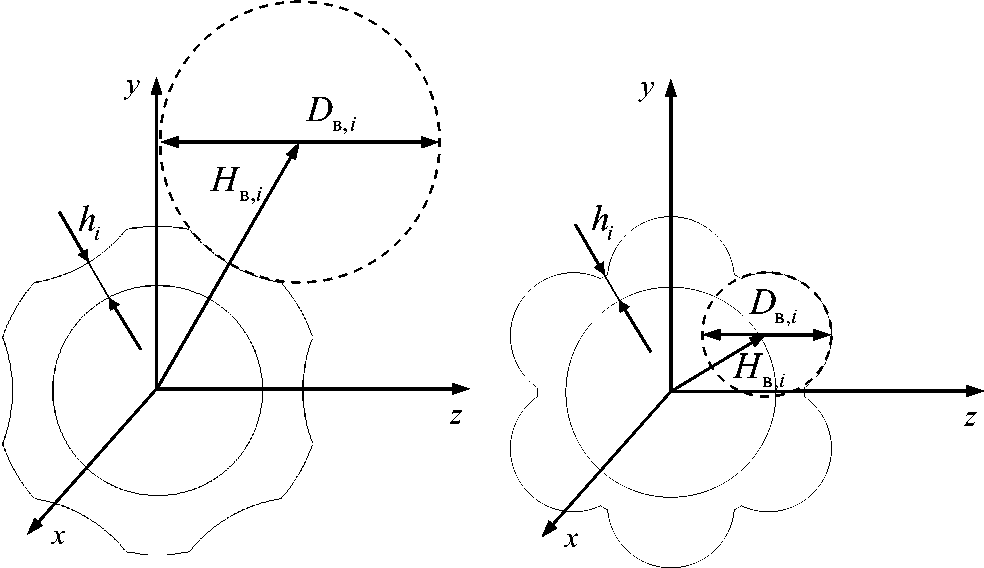
Для стволов с ребрами жесткости в качестве управляемых переменных помимо внешних диаметров D i (см. рис. 2) также рассмотрим: D_вi - диаметр вырезаемой (добавляемой) окружности на i -ом поперечном срезе и расстояние от центра канала ствола до центра вырезаемой (добавляемой) окружности H . , i = 0, N (рис. 3), тогда, x = ( D 0 , D   D_N , D ,„ , D ,'„ ., D , _Л , H „, H _M, .. H . N ).

Сформулируем ограничения задачи оптимизации. Слишком малые внешние диаметры и, следовательно, толщины ствола могут привести к его разрушению. Чтобы определить минимальную допустимую толщину ствола воспользуемся теорией наибольших деформаций [8]. С запасом прочности к = 1,2 наименьшая толщина классического ствола h _{min i} в i -ом сечении рассчитывается по формуле:

,        Dmin,i - di mn, min,i            2        ,

D =d min,i        i

1,5 o _e + k ■ p m max,7_ \ ^1,5 ° e ^{- 2} k ■ P max i’

i = 0, N , (15)

а)                               б)

Рис. 3. Определение управляемых переменных для ствола с ребрами жесткости: а) 1-го типа; б) 2-го типа

где d_i – внутренний диаметр в i -ом сечении камеры или ствола; p _{max, i} – максимальное давление в i -ом сечении; ст e - предел пропорциональности материала ствола.

Также введем ограничение на массу ствола. Поскольку слишком массивный ствол ухудшает подвижность артиллерийской установки и повышает стоимость производства, поэтому целесообразно ввести максимально допустимую массу ствола m _max.

Тогда система ограничений Г для задачи оптимизации формы ствола будет следующей:

h > hmin,1, i = 0, N, m < m max ,

где h_i – толщина ствола в i -ом сечении.

Сформулируем критерий оптимизации. Основной задачей исследования является уменьшение разброса снарядов при стрельбы очередями из автоматической пушки, то есть повышение кучности стрельбы. При этом колебания ствола вносят значительный вклад в начальные условия движения снаряда на внешнебаллистической траектории. Начальное положение, направление и скорость движения снаряда, зависят от колебания ствола, а именно от положения дульного среза в момент выхода снаряда из ствола автоматической пушки. Полагая, что разброс снарядов в среднем снижается с уменьшением амплитуды колебаний дульного среза ствола, в качестве целевой функции оптимизации рассмотрим функцию вида:

A = f ^{( x )} = ma/^ ⁽ V _д ( t ^, x )^- v ₀ ( x ) )² + ( u ( t , x )^- w ₀ ( x ) ) ² ) ^ min ,(17)

где v _д( t , x ), w _д( t , x ) – перемещения дульного среза в плоскостях Oxy и Oxz соответственно для рассматриваемого вектора x ; v ₀( x ), w ₀( x ) – начальное положение дульного среза в плоскостях

Oxy и Oxz соответственно для рассматриваемого вектора x .

• 3. МЕТОД РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ ФОРМЫ СТВОЛА

При поиске оптимальной формы ствола необходимо учитывать несколько факторов. Во-первых, моделирование процесса выстрела требует больших затрат времени, что делает не- возможным применение эвристических алгоритмов оптимизации, таких, как генетический алгоритм, метод роя частиц и др. Во-вторых, информация о виде и градиенте функции не- известна, что затрудняет применение градиентных методов оптимизации. В-третьих, масса и толщина ствола произвольной формы рассчитывается на основе триангуляции Делоне и зависимость между ними и управляемыми пе- ременными неизвестна, что затрудняет применение методов линейного программирования. Таким образом, для решения рассматриваемой задачи предпочтительнее использовать эффек- тивные методы оптимизации, позволяющие найти решение за малое количество вычислений функции.

В данной заботе рассмотрим алгоритм оптимизации Нелдера-Мида [14], в основе которого лежит построение n -мерного симплекса с n + 1 вершиной. По результатам сравнения значений функции в вершинах происходит одна из операций: растяжение, сжатие, отражение или редукция (глобальное сжатие) симплекса.

Для учета ограничений воспользуемся методом штрафных функций:

’f = f(x \    x e Г,

".f = f (x)+ Fm,x6 Г, где Fш – штрафная функция, принимающая достаточно большое значение, которое позволяет исключить выход вектора управляемых параметров за ограничения Г. В работе значение штрафной функции принималось равным Fш = 1 000 000.

Рассмотрим шаги алгоритма оптимизации Нелдера-Мида.

Шаг 1. Задается длина ребра L и начальная точка x ₀, далее строится начальный симплекс:

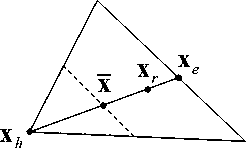
Рис. 4. Растяжение симплекса (в двумерном пространстве)

^

d 1 =

x ij

xij

V n + 1 - 1

n

L , d ₂

V n + 1 + n - 1 l n V2

= x O j

+ d1,

— x о j + d 2

i * j, i — j,

i — 1, n ,   j — O, n - 1,

где x_ij – значение j -й координаты x _i . После чего, вычисляются значения функции f_i = f ( x _i ) в точках x _i .

Шаг 2. Определяется точка x _l с наименьшим значением функции f_l , точка x _h с наибольшим значением функции f_h и точка x _g следующим за наибольшим значением функции f_g .

Шаг 3. Вычисляется центр тяжести по точкам без точки x h и значение функции f = f ( x ) _:

x =

n + 1 ¹ X n i = 0, i * h

x _i .

Шаг 4. Вычисляются координаты x _r и значение функции f_r отраженной точки x _h относительно x в данной точке.

X r — ( 1 + C _0Tp ) x - C _отр X h ,         (21)

где C _отр – коэффициент отражения, как правило, равен 1.

Шаг 5. Если f_r< f_l , тогда необходимо растянуть симплекс (рис. 4) в направлении x _r , для этого необходимо рассчитать координаты точки x _e и значение функции f_e .

X e — C p.. X r + ( 1 - C p„ ) x ,         (22)

где C _рас – коэффициент растяжения, как правило, больше 1.

Шаг 6. Если f_e< f_l , тогда точка x _h заменяется на x _e , f_h на f_e и проверить условие завершения расчета. Если условие завершения не выполняется, то происходит переход на шаг 2.

Шаг 7. Если f_g > f_r > f_l , тогда точка x _h заменяется на x _r , f_h на f_r и проверить условие завершения расчета. Если условие завершения не выполняется, то происходит переход на шаг 2.

Шаг 8. Если f_r > f_l , f_r > f_g и f_r< f_h , тогда точка x _h заменяется на x _r , f_h на f_r .

Шаг 9. Проводится сжатие симплекса (рис. 5) и определяется точка x _c и f_c по формуле:

^X c

^X c

— C „X h + ( 1 - C„ ) x , f, > f h , ₍₂3) ^{— C} ™„^X , ^{+ ( 1 - C} ™„ К f , S f h ^, ’

где C _сжат – коэффициент сжатия, как правило меньше 1.

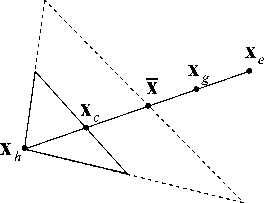
Рис. 5. Сжатие симплекса (в двумерном пространстве)

Шаг 10. Если f_c <  f_h , тогда точка x _h заменяется на x _c , f_h на f_c и проверяется условие завершения. Если условие завершения не выполняется, то происходит переход на шаг 2.

Шаг 11. Проводится редукция симплекса по формуле

X = x^ , i = 0, n ,

определяется значение функции f_i и проверяется условие завершения:

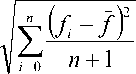
где s - заданная точность расчета; f =----X fi n +1 i=0

– среднее значение функций f_i . Если условие (25) не выполняется, то происходит переход на шаг 2.

4. МОДЕЛИРОВАНИЕ СТРЕЛЬБЫ АВТОМАТИЧЕСКОЙ ПУШКИ

В качестве объекта моделирования будем рассматривать 30-мм автоматическую пушку, геометрия которой представлена в таблице 1. Угол возвышения задавался равным ф = 20 градусов, интервал между выстрелами – 182 мс. Свойства материала ствола принимались постоянными: плотность р = 7850 кг/м³, модуль Юнга E = 200 ГПа, коэффициент Пуассона v = 0,3, ко-

Таблица 1. Геометрия ствола 30-мм автоматической пушки

Координата сечения x, мм Внутренний диаметр di, мм Внешний диаметр Di, мм 0 40 125 127 40 125 147 30 86 339 30 71 1000 30 45 2400 30 40 эффициент линейного теплового расширения α = 12,5.10-6 K-1, теплоемкость c = 567 Дж/(кг.К), теплопроводность λ = 32 Вт/(м.К).

Давление и температура пороховых газов определялись на основе решения основной задачи внутренней баллистики [15] в термодинамической постановке [16]. Численное решение задачи внутренней баллистики получено явным методом Рунге-Кутта 4-го порядка. Расчет колебания ствола автоматической пушки с учетом теплового нагружения проводился на основе одномерной математической модели [4, 10]. Численное решение колебаний и теплового нагружения ствола получено интегро-интерполяционным методом [17]. Внешнебаллистическая траектория определяется из решения уравнений движения снаряда [18] с учетом колебания относительно центра масс [19] при начальных условиях, определяемых из решения задачи колебания ствола. Численное решение задачи внешней баллистики получено явным методом Рунге-Кутта 4-го порядка.

• 5. РЕЗУЛЬТАТЫ ОПТИМИЗАЦИИ ФОРМЫ СТВОЛА

В качестве максимальной допустимой массы mmax примем исходную массу классического ствола m0 = mmax = 36 кг. График убывания целевой функции – амплитуды колебаний дульного среза в зависимости от итерации для различных форм ствола представлен на рис. 6.

Из рис. 6 видно, что через 500 итераций значение целевой функции устанавливается на 254,4 мкм для классического ствола, на 242,1 мкм для ствола 8 ребрами жесткости 1-го типа и на 241,6 мкм для ствола 3 ребрами жесткости 2-го типа.

На рис. 7 представлено сравнение исходной и оптимальной геометрии классического ствола.

Из рис. 7 видно, что у оптимального классического ствола диаметр каморы на 23 мм меньше, чем у исходного ствола, а диаметр в средней части и у дульного среза, наоборот больше на 2,5 – 10 мм.

Отобразим на рис. 8 ствол с 8 ребрами жесткости 1-го типа и ствол с 3 ребрами жесткости 2-го типа, полученные в результате оптимизации.

Результаты оптимизации амплитуды колебаний A и разброса снарядов r ₁₅₀₀ на расстоянии 1 500 м за счет добавления ребер жесткости представлены в таблице 2.

Из таблицы 2 видно, что применение ребер жесткости 1-го типа дополнительно сокращает амплитуду на 4,8% относительно классического ствола, при этом разброс снарядов сокращается на 15,9%. Применение ребер жесткости 2-го

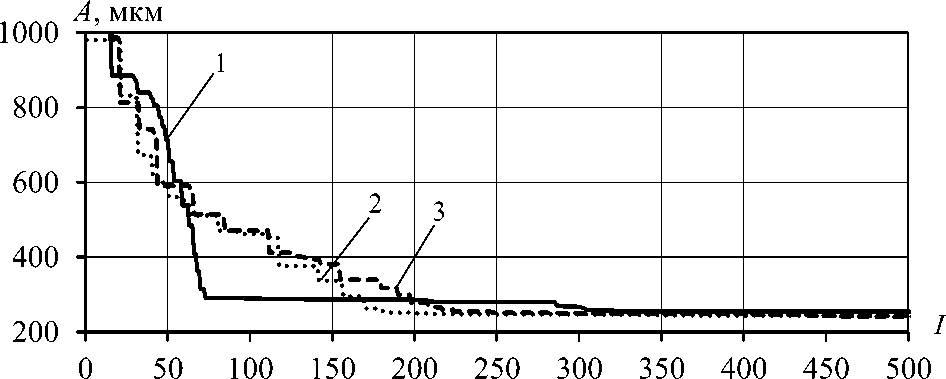
Рис. 6. График убывания целевой функции:

1 – классический ствол; 2 – ствол с 8 ребрами жесткости 1-го типа;

3 – ствол с 3 ребрами жесткости 2-го типа

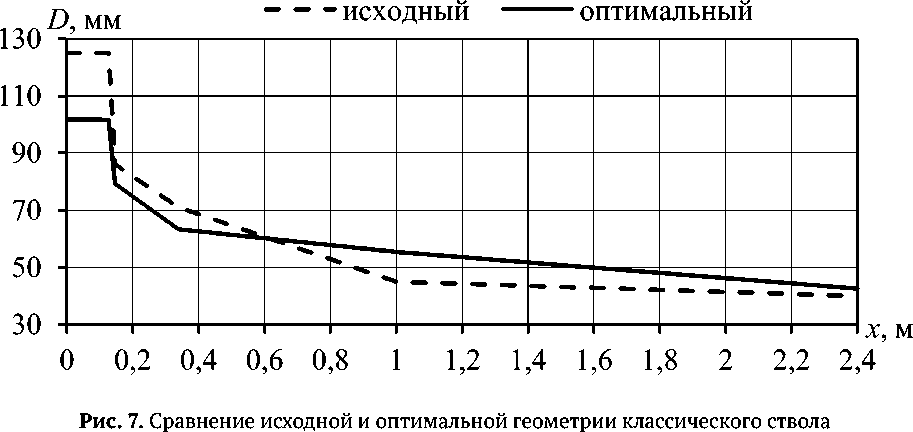
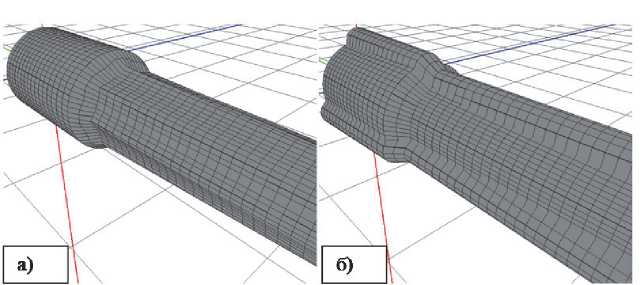
Рис. 8. Оптимальные формы ствола:

а) ствол с 8 ребрами жесткости 1-го типа; б) ствол с 3 ребрами жесткости 2-го типа

типа сокращает амплитуду на 5,0%, при этом разброс снарядов сокращается на 12,1%.

На рис. 9 представлен разброс снарядов при стрельбе на расстоянии 1 500 м для различных стволов.

Как показали расчеты, оптимизация классического ствола позволяет сократить амплитуду колебаний А на 44,4% с 457,8 мкм до 254,4 мкм, при этом разброс снарядов r 1500 на расстоянии 1 500 м сокращается на 61,2% с 1,102 м до 0,428 м.

Исследуем зависимость амплитуды колебаний и разброса снарядов от допустимой массы m max ^е [ 0,75 m ₀ ;l,25 m ₀ ] оптимизированных классических стволов. Результаты исследования представлены на рис. 10.

Из рис. 10 видно, что амплитуда оптимального классического ствола массой 28 кг равна амплитуде исходного классического ствола массой 36 кг (А = 457,8 мкм), т.е. масса ствола может быть снижена на 8 кг (22,2%) без увеличения амплитуды колебаний. При увеличении массы ствола на 0,8 кг (2,2%) амплитуда колебаний становится равной амплитуде колебаний ствола с 8 ребрами жесткости 1-го типа (А = 242,1 мкм) (см. таблица 2).

На рис. 11 представлено сравнение геометрии классических стволов различной допустимой массы.

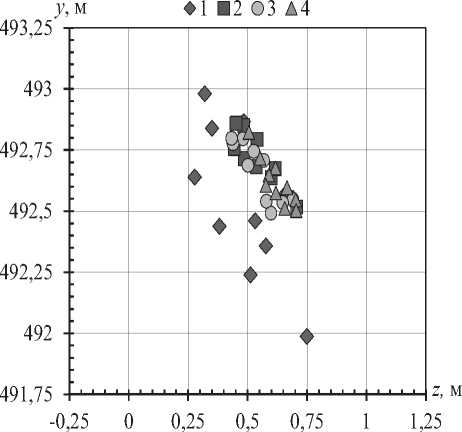
Рис. 9. Разброс снарядов при стрельбе на расстоянии 1 500 м после оптимизации: 1 – исходный классический ствол;

2 – классический ствол после оптимизации; 3 – оптимальный ствол с 8 ребрами жесткости 1-го типа; 4 – оптимальный ствол с 3 ребрами жесткости 2-го типа

Таблица 2. Результаты оптимизации амплитуды колебаний за счет ребер жесткости

Количество ребер жесткости	Ребра жесткости 1-го типа		Ребра жесткости 2-го типа
	A, мкм	Г 1500 , м	A , мкм	Г 1500 , м
3	249,1	0,490	241,6	0,376
4	254,3	0,446	242,8	0,394
5	249,4	0,382	247,8	0,397
6	243,2	0,478	243,1	0,895
7	243,7	0,414	244,2	0,879
8	242,1	0,360	253,6	0,606
9	246,3	0,337	254,2	0,486
10	250,5	0,458	243,8	0,831

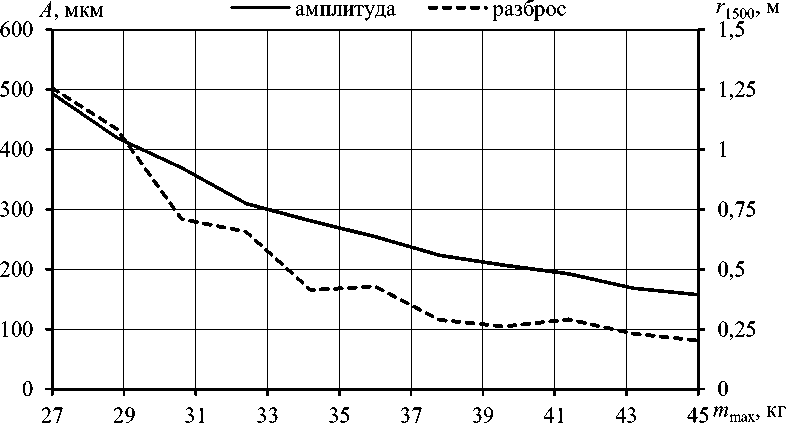
Рис. 10. Зависимость амплитуды колебаний дульного среза классического ствола и разброса снарядов от допустимой массы

Из рис. 11 видно, что при изменении допустимой массы ствола в основном изменяется внешний второй половины ствола, при этом диаметр казенной части остается почти без изменений.

На рис. 12 представлен разброс снарядов при стрельбе на расстоянии 1 500 м для классических стволов различной допустимой массы.

Как показали расчеты, разброс снарядов на расстоянии 1 500 м для оптимального классического ствола массой 28,5 кг равен разбросу снарядов для исходного классического ствола массой 36 кг ( r ₁₅₀₀ = 1,102 м), т.е. масса ствола может быть снижена на 7,5 кг (20,8%) без увеличения разброса снарядов. При увеличении мас-

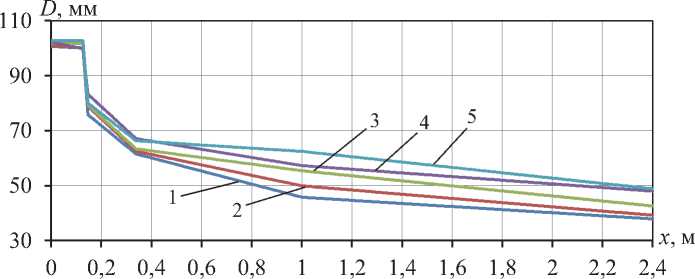
Рис. 11. Сравнение геометрии классических стволов оптимальной формы и различной допустимой массы:

1 – 27 кг; 2 – 30,6 кг; 3 – 36 кг; 4 – 41,4 кг; 5 – 45 кг

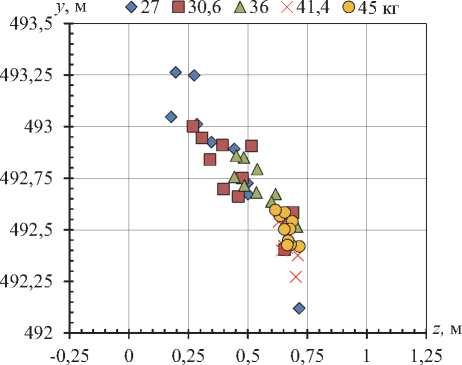
Рис. 12. Разброс снарядов при стрельбе на дальность 1 500 м для оптимальных классических стволов различной допустимой массы

сы ствола на 0,7 кг (1,9%) разброс снарядов становится равным разбросу снарядов для ствола с 8 ребрами жесткости 1-го типа ( r ₁₅₀₀ = 0,360 м) (см. таблица 2).

ЗАКЛЮЧЕНИЕ

В работе рассмотрен алгоритм многопараметрической безградиентной оптимизации геометрической формы ствола на основе метода Нелдера-Мида и метода штрафной функции с учетом ограничений на толщину стенки и массу ствола. Рассмотрены классическая форма ствола и 2 типа стволов с ребрами жесткости.

В качестве целевой функции была выбрана амплитуда колебаний дульного среза ствола, полученная в результате моделирования очереди из 10 выстрелов из 30-мм автоматической пушки. Силовое и тепловое нагружение ствола определялось из решения задачи внутренней баллистики в термодинамической постановке, колебания ствола моделировались по ква-зиодномерной математической модели, разброс снарядов определялся из решения задачи внешней баллистики с учетом колебаний ствола. Оптимизация классического ствола позволяет сократить амплитуду колебаний на 44,4% с 457,8 мкм до 254,4 мкм, при этом разброс снарядов на расстоянии 1 500 м сокращается на 61,2% с 1,102 м до 0,428 м.

Получены оптимальные размеры стволов с ребрами жесткости 1 и 2 типов. Показано, что применение ребер жесткости 1-го типа дополнительно сокращает амплитуду на 4,8% относительно классического ствола, при этом разброс снарядов сокращается на 15,9%. Применение ребер жесткости 2-го типа сокращает амплитуду на 5,0%, при этом разброс снарядов сокращается на 12,1%.

Показано, что масса классического ствола может быть снижена на 8 кг (22,2%) без увели- чения амплитуды колебаний, а при увеличении массы ствола на 0,8 кг (2,2%) амплитуда колебаний становится равной амплитуде колебаний ствола с 8 ребрами жесткости 1-го типа.

Из полученных результатов видно, что выбор геометрии и формы ствола существенно влияет на колебания ствола и разброс снарядов при поражении цели.