Метод нелинейной диэлектрической спектроскопии для исследования сегнетоэлектриков в случае сильных полей

Основными свойствами сегнетоэлектриков, благодаря которым они используются в технике, являются наличие спонтанной поляризации P_s , большая диэлектрическая проницаемость Е , зависимость Е и P s от напряженности электрического поля E . Одним из наиболее чувствительных методов исследования е ( E , Т) и P s ( E , Т) является метод нелинейной диэлектрической спектроскопии (НДС), который позволяет достаточно полно исследовать сегнетоэлектрические фазовые переходы. Суть метода НДС заключается в генерации гармоник второго и более высоких порядков. Анализируя зависимость гармоник от температуры, можно определять тип фазового перехода и рассчитывать коэффициенты разложения Ландау-Гинзбурга [1, 2]. Метод НДС также позволяет определять температуру исчезновения P_s , поэтому его удобно использовать для исследования как объёмных, так и наноструктурированных сегнетоэлектриков.

В настоящее время теоретически получены точные значения амплитуд высших гармоник для сегнетоэлектриков первого и второго рода в случае малых модулирующих полей ( E << E_c) [3-5], однако отсутствует теория метода НДС для сильных полей ( E > E_c) . Сложность получения точного решения состоит в том, что для реального кристалла форма петли гистерезиса зависит от при- Милинский Алексей Юрьевич, кандидат физико-математических наук, доцент кафедры физики.

месей, дефектов, частоты переключения P_s и т.д. Цель данной работы – экспериментальное определение температурной зависимости коэффициента третьей гармоники у _{3 ю} для различных сегнетоэлектриков при модулирующих полях, больших коэрцитивного. В качестве объектов исследования были выбраны следующие вещества: сегнетоэлектрик второго рода триглицинсульфат – TGS; сегнетоэлектрик первого рода титанат бария – BaTiO₃; сегнетоэлектрик с двумя областями сегнетофазы тиомочевина – SС(NH₂)₂; антисегнетоэлектрик цирконат свинца – PbZrO₃. Выбор исследуемых веществ определялся тем, что в литературе имеются данные о температурной зависимости их спонтанной поляризации вблизи фазового перехода, а также с целью проверки применимости метода НДС для определения температурного хода P_s в различных сегнетоэлектриках.

• 2.    ТЕОРИЯ

Для сегнетоэлектрика нелинейная поляризация или индукция выражается нечетным степенным рядом по напряженности поля

D = £ 0 E + ( P s + X i E + / з E ³ + % 5 E ⁵ + ...) , (1) где P_s – спонтанная поляризация, коэффициент % 1 обозначает линейную диэлектрическую восприимчивость, а % 3 и % 5 - диэлектрические восприимчивости третьего и пятого порядков, соответственно.

Согласно феноменологической теории Ландау-Гинзбурга, вклад в свободную энергию сегнетоэлектрика, обусловленный поляризацией Р , может быть представлен в виде [6]

Ф = F + - аР ²+ -в Р ⁴+¹ YP ⁶+ ( gradP) 2 ~ EP, ^о 2 4 6 (2)

а = ао (T - Tо), где Е – напряженность электрического поля, P – поляризация решетки, имеющая смысл параметра упорядочения, коэффициенты а о, Р и У зависят от температуры Т. Слагаемое (gradP)2опи-сывает флуктуации поляризации, которые должны играть наиболее существенную роль в области температуры Кюри. Разложение (2) справедливо вблизи от точки перехода То, причём при Р > 0 и у — 0 оно описывает фазовый переход второго рода, а при Р < 0 и У > 0 -переход первого рода.

Слабые поля. Для электрического поля много меньшего, чем коэрцитивное E << E_c , переключение поляризации не имеет места. Минимизируя свободную энергию (2), легко найти уравнение состояния в элек-трическом поле

E = P [а + в P ² + Y P 4 ] . (3)

Чтобы получить нелинейный вклад, не-обхо-димо найти производную по полю от диэлектрической восприимчивости % , которая определяется из (3) дифференцированием по поляризации:

dP             dE

P = % E     % = — X =-т^

dE                dP ,

(4) . dE

X ^_ = — = а + 3в P ² + 5у P ⁴.

Интересующая нас производная получается дифференцированием выражения, обратного к (4), то есть

= dP =       ¹

• % = dE ~ а + 3в P ² + 5y P⁴ ’

d y = d y dP    ^з (₆в p + 20y p 3)

dE dP dE                 ^.

В (5) поляризация зависит от поля в соответствии с уравнением состояния (2), однако при малых полях поляризацию можно выразить в приближенном виде

Р = P s +E % ,             (6)

где Рs отлична от нуля только в сегнетоэлектрической фазе. Учитывая (6), соотношение (5) примет вид dy = _XWPs + EX) + 20y(P,+ EX)3]. (7) dE

В случае нелинейных диэлектриков емкость образца является функцией напряжения. Принимая это во внимание, емкостная компонента тока через образец может быть представлена в виде [5]

I = d ( CU ) = С dU dCdU

C dt 0 dt ° dU dt ’

где Со = C (U = 0). Последнее слагаемое отражает нелинейный вклад и проявляется в возникнове- нии гармоник. Нелинейный вклад в ток через образец, будет определяться соотношением

„ U ² . ,        d%

I = ю S —у sin(2 ю t ) ——,         (9)

нелин           h²            ’ dE               ⁽ )

где S и h – площадь и толщина образца, соответственно. Если поле изменяется по гармоническому закону E = Eosin( to t), то выражение (9) с учетом (8) примет вид и2,

Анелин =_[юSUt sln(2ю t )6вPsX + юSU- 6вE°% 4-(cos(ю t) - cos(3ю t)) + hh

U2                       U21

+ юS -°- 20yP3%3 sln(2юt) + юS-°-60yP,2Eo%4 - (cos(mt) _ cos(3юt)) + h2                            h22

’

+ юS -°- 60yPE %5 ' (2 sln(2ю t) _ sш(4ю t)) + h2

_ U2 _ _ , . 1 _                   _ __

+ ю S     20y E 3 % ^ (2 cos(ю t ) _ 3 cos(3ю t ) + cos(5ю t ))].

Группируя токи, соответствующие высшим гармоникам (2 to , 3 to , 4 to , ...), получим

U2             ,,

1 ₂ю =_ 2[ю S -f 81п(2ю t ){% ³<3P P s + 10y P s ³) + 15y P s X ⁵ -f }] ,(10) hh

U3          -            15

I3ю = 3% юSTTcosOt){в + 10YPs } + — юS-pYX cosOt),(11) h2

U ⁴

14m = 15®S-y yPsX5sin(4®t),(12)

h

5 . „U5.

I5ю = _TYX юSTTcos(5«t).(13)

2 h

Сильные поля. Для случая полей, больших коэрцитивного, в разложении (6) нельзя пренебрегать старшими членами и необходимо учитывать переключение спонтанной поляризации P s , т.е. dPs/dt Ф 0. Ток через образец в случае гармонического поля будет определяться токовой петлей гистерезиса.

Из теории гармонического анализа известно, что любой сигнал, выраженный функцией от времени, можно представить в виде суммы гармонических составляющих, отличающихся друг от друга амплитудой, частотой и начальной фазой. В случае периодической функции j ( t ) с периодом Т её спектр состоит из бесконечного числа гармонических составляющих, частоты которых равны n to , где to = 2 Я J T ( п = 1, 2, 3.). Амплитуды спектральных составляющих являются в этом случае коэффициен-тами ряда Фурье [7]

^

^{j (} t ) =   ⁺ S ^jn ^cos( n ° t ^_Ф n ) ,   (14)

²     n = 1

где j _о – плотность тока на нулевой частоте, j_n – амплитуда n -ной гармоники тока.

2 t jo = - J j(t)dt,   jn = Van + bn ,

T 0

b

1дф = an ,

an

2 t                         2 t

= — j j ( t ) Cos ( n to t ) dt , b_n = — j j ( t ) Sin ( n to t ) dt .

T 0_q                           T 0_q

Если переключение поляризации аппроксимировать прямоугольными импульсами, то амплитуда гармоник будет определяться выражением

n   nn

2 j _max π n

sin

n ° t_u

где j _max – амплитуда токовых импульсов, определяемая величиной спонтанной поляризации P _s, формой петли гистерезиса и временем переключения P _s.

Согласно соотношению (16), амплитуды гармоник j_n будут периодически меняться, и уменьшаться с увеличением n, а амплитуды всех гармоник в сегнетофазе при больших полях ( E >  E _c) будут пропорциональны спонтанной поляризации P _s. Если положить, что длительность импульса t = Т/2, то из (16) следует, что максимум амплитуды будет приходиться на третью гармонику.

3. СРАВНЕНИЕ ТЕОРИИ И ЭКСПЕРИМЕНТА

Установка для исследований температурных зависимостей амплитуд высших гармоник включала в себя генератор с максимальным выходным напряжением 10 В и повышающий трансформатор с коэффициентом трансформации 20. При исследовании на образцы подавалось поле напряженностью 2000 В/см. Сигнал кратных гармоник снимался с резистора, включенного последовательно с образцом, и подавался на цифровой анализатор спектра, в качестве которого служил ком-

пьютер с 24-разрядным АЦП ZET 230 и программным обеспечением ZetLab. Для проведения измерений была выбрана частота 2 кГц, что обусловлено временами переключения поляризации в сегнетоэлектриках и характеристиками измерительной системы. Более подробное описание установки приведено в [8]. В качестве электродов применялась In-Ga паста. Измерения проводились в режиме непрерывного охлаждения и нагрева в температурном интервале, охватывающем фазовые переходы. Скорость изменения температуры была не более 1 K/мин. Точность определения температуры составляла около 0.2 K.

Триглицинсульфат. Триглицинсульфат представляет собой классический сегнетоэлектрик с фазовым переходом второго рода и уже в течение долгого времени является объектом активных теоретических и экспериментальных исследований. Выше температуры Кюри ( Т с = 322 К) кристалл TGS имеет моноклинную симметрию и принадлежит к центросимметричному классу 2/ m . Ниже Т _с кристалл принадлежит к полярной точечной группе 2 моноклинной системы (зеркальная плоскость исчезает). Полярная ось лежит вдоль моноклинной оси 2-го порядка. Одна элементарная ячейка кристалла TGS содержит более 100 атомов. Структура TGS сложна и представляет собой сетку молекул глицина CH₂NH₂COOH и тетраэдров SO₄, связанных между собой водородными связями типа О-H...О и N-Н [9].

На рис.1 представлены результаты исследования монокристалла TGS в температурном ин-

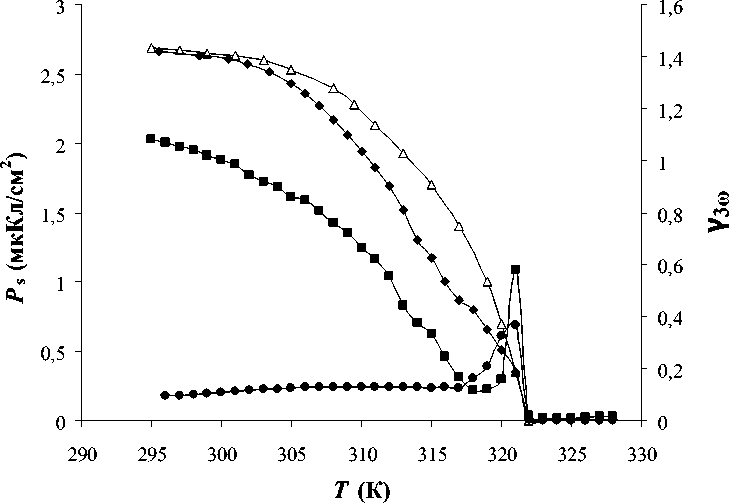
Рис. 1. Температурный ход коэффициента третьей гармоники у _{3 ю} для монокристалла TGS для разных величин приложенного поля: Е << E c (круги), Е = E c (квадраты), E > E c (ромбы) в сравнении с зависимостью P _s( Т ) [9] (треугольники)

тервале от 293 К до 333 К для разных полей. Измерения при разных значениях напряженности электрического поля проводились с целью показать, что результаты метода НДС, в частности форма кривой у _{3 ю} ( Т) зависит от того, при каком поле получена кривая.

В [3] были получены соотношения для 8 3 через коэффициенты Ландау-Гинзбурга для фазового перехода второго рода

• 8 з =-% 4 ( Р8 о - 18 %Р 2 P s 2 8 0 ) . ⁽¹⁷⁾

Используя выражение для спонтанной поляризации через коэффициенты разложения Ландау-Гинзбурга, можно получить, что 8 3 = 8 Р^ ⁴ f ₀ ниже фазового перехода и 8 3 = - 3% ⁴ f 0 выше фазового перехода. Выражение (17) показывает, что модуль амплитуды третьей гармоники должен возрастать при приближении к фазовому переходу со стороны сегнетофазы и обращаться в ноль при переходе.

Проведенные исследования показали, что для монокристалла TGS при приложении переменного поля ( Е << E _c) вдоль P _s максимум сигнала на основной частоте совпадает с температурой фазового перехода, а амплитуда третьей гармоники имеет максимум несколько ниже Т _с (при 320321 К) и обращается в ноль при Т _с = 322 К (рис.1). Такое поведение третьей гармоники в целом согласуется с выражением (17). При увеличении модулирующего поля амплитуда третьей гармоники сначала возрастает пропорциональна Е , затем выходит на насыщение при Е = E c . С увеличением температуры у _{3 ю} монотонно убывает, но как в случае слабых полей имеет максимум перед фазовым переходом, обращаясь в ноль при 322 К (рис. 1).

Для поля E > E _c, приложенного вдоль P_s , амплитуда третьей гармоники у _{3 ю} монотонно уменьшается и обращается в ноль при Т _с. Температурная зависимость у _{3 ю} достаточно хорошо согласуется с температурным ходом спонтанной поляризации P _s, что подтверждает теоретические результаты метода НДС в случае полей, больших коэрцитивного.

Титанат бария. В кристаллах BaTiO3 наблюдаются три фазовых перехода типа смещения, сопровождающихся изменением структуры и свойств [10]. Титанат бария имеет несколько равноправных направлений поляризации и является примером многоосного сегнетоэлектрика. При температурах выше 393 К титанат бария имеет кубическую кристаллическую структуру типа перовскита. Такая параэлектрическая модификация относится к пространственной группе Pm3m. Ниже температуры перехода Тс = 393 К происходит фазовый переход, и до температуры 278 К BaTiO3 является сегнетоэлектриком, имеющим тетрагональную симметрию класса P4mm. При искажении формы кубической ячейки ниже 393 К скачком возникает спонтанная поляризация Ps, величина которой плавно нарастает от 18 мкКл/ см2 вблизи Тс до примерно 26 мкКл/см2 при комнатной температуре. При температурах ниже 278 К происходит второй фазовый переход, кристалл становится ромбическим. В интервале температур от -343 К до -363 К титанат бария испытывает третий фазовый переход и ниже этих температур имеет ромбоэдрическую структуру. При всех переходах имеет место температурный гистерезис [10].

На рис. 2 представлена температурная зави симость коэффициента третьей гармоники у3ю для монокристалла BaTiO3 в сравнении с теоретической зависимостью спонтанной поляризации монокристалла титаната бария

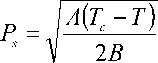
где Т _с – температура Кюри, А и В – постоянные, определяемые эмпирически.

Из графика видно, что теоретическая зависимость (18) в пределах погрешности достаточно хорошо согласуется с температурным ходом у _{3 ю} , полученным в ходе эксперимента. Это подтверждает предположение, что при полях, больших коэрцитивного, температурная зависимость амплитуды третьей гармоники около фазового перехода пропорциональна спонтанной поляризации P _s.

Тиомочевина. Кристаллы тиомочевины SС(NH₂)₂ обнаруживают сложную последовательность структурных фазовых переходов [11]. При комнатной температуре кристалл принадлежит к центросимметричной группе Рnта с параметрами ячейки а = 7,65 A^o , b = 8,53 A^o , с = 5,52 A^o (фаза V). При понижении температуры между 202 K и 180 K появляется неполярная фаза (фаза IV). Между 180 K и 176 K формируется полярная фаза (фаза III) со значением спонтанной поляризации Р _s = 2,5·10^-9 Кл/см². Между 176 K и 169 K неполярная фаза (фаза II) и ниже 169 K полярная фаза (фаза I) со спонтанной поляризацией вдоль оси а , равной Р _s = 3·10^-6 Кл/см² [11].

Для исследований методом НДС использовался монокристалл тиомочевины, выращенный при комнатной температуре из водного раствора. Результаты измерения температурного хода коэффициента третьей гармоники у _{3 ю} вдоль сегнетоэлектрической оси а в сравнении с зависимостью P _s( T ) представлены на рис.3. Формы кривых достаточно хорошо согласуются между собой. В интервале температур 180 и 176 К коэффициент третьей гармоники имеет как и спонтанная поляризация аномалию, которая соответствует формированию сегнетоэлектричес-

0,35

0,3

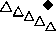
0,25

0,2

s

0,15

0,1

0,05

300        320        340        360        380        400

Т (К)

Рис. 2. Температурный ход коэффициента третьей гармоники у _{3 ю} для монокристалла BaTiO 3 (треугольники) в сравнении с теоретической зависимостью (18) (ромбы)

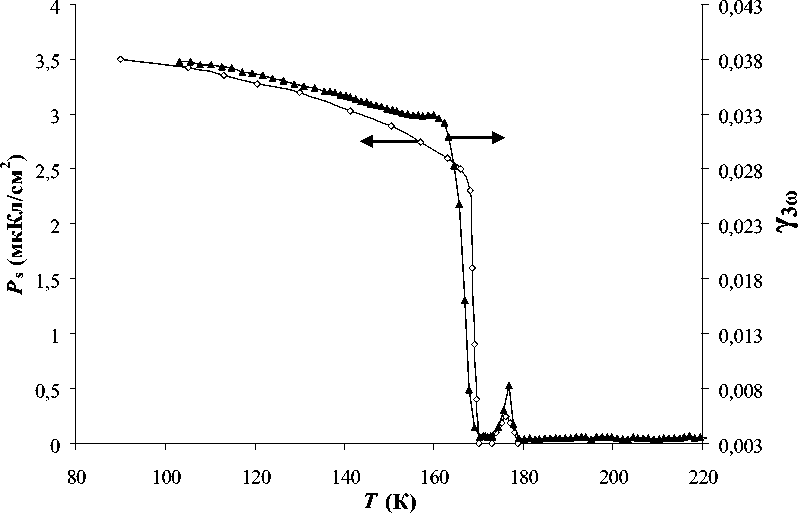
Рис. 3. Температурный ход коэффициента третьей гармоники у _{3 ю} для монокристалла SC(NH₂)₂ вдоль сегнетоэлектрической оси а (треугольники) в сравнении с зависимостью P _s( Т ) [11] (ромбы)

кой фазы III. Величина у _{3 ю} в этой температурной области значительно меньше, чем в фазе I, что связанно со значением спонтанной поляризации в фазе I. Необходимо отметить, что аномалий коэффициента у _{3 ю} вдоль других осей монокристалла не наблюдалось, что связанно с одно-осностью монокристалла SС(NH₂)₂.

Цирконат свинца. Цирконат свинца

(PbZrO3) является веществом, в котором впервые было открыто антисегнетоэлектрическое состояние [12] и он считается наиболее исследованным антисегнетоэлектриком. При высоких температурах PbZrO3 обладает кубической структурой перовскита, при понижении температуры характеризуется чёткой диэлектрической аномалией вблизи 503 К. Высокотемпературная фаза является параэлектрической с диэлектрической проницаемостью, описываемой законом Кюри-Вейсса с константой Кюри 1,6·105 град и температурой Вейсса 463 К. В ранних экспериментальных работах на керамических образцах PbZrО3 было установлено, что фазовый переход при 503 К является единственным при изменении температуры в слабом поле, и что приложение внешнего электрического поля ниже Тс индуцирует переход в ромбоэдрическую сегнетофазу. Это позволило предположить, что антисегнето-и сегнетоэлектрическая фазы имеют почти равные свободные энергии, что хорошо согласуется с классической моделью антисегнетоэлектричества. В [13-15] было показано, что ромбоэдрическая сегнетофаза может быть стабильной ниже 503 К при слабых полях в узком промежуточном температурном интервале шириной 10-25 К. В связи с вышеизложенным перед нами стояла задача проверить возможности метода НДС для регистрации сегнетоэлектрического состояния в PbZrO3. В качестве объекта исследования были выбраны керамические образцы цирконата свинца.

На рис. 4 представлены температурные зависимости коэффициента третьей гармоники Y^o, измеренные для разных величин приложенного поля. Результаты Y3o (Т) указывают, что в температурной области 503-489 К величина коэффициента третьей гармоники имеет аномалию, связанную с возникновением спонтанной поляриза- ции. Температурный интервал 503-489 К, в котором наблюдается аномалия, хорошо согласуется с литературными данным [13-15]. При увеличении напряженности модулирующего поля до значения, сравнимого с коэрцитивным, коэффици ент Y3o выходит на насыщение. При дальнейшем увеличении поля максимальное значение Y3o меняется слабо. Необходимо отметить, что при полях, напряженность которых выше 300 В/см, третья гармоника в антисегнетоэлектрической фазе имеет небольшую аномалию с максимумом коэффициента Y3o около 470-475 К. Очевидно, что метод генерации третьей гармоники позволяет уверено регистрировать сегнетоэлектрическое состояние, возникающее в антисегнетоэлектриках. На вставке рис. 4 пунктирными линиями на кривой Е (Т) показан температурный интервал сегнетоэлектрической фазы.

• 5.    ЗАКЛЮЧЕНИЕ

Таким образом, в настоящей работе теоретически и экспериментально показано, что в случае полей, больших коэрцитивного, метод НДС позволяет определить температурный ход спонтанной поляризации. Зависимость Y _{3 o} ( Т ) около фазового перехода дает хорошее согласие с зависимостью спонтанной поляризации P _s от темпе-

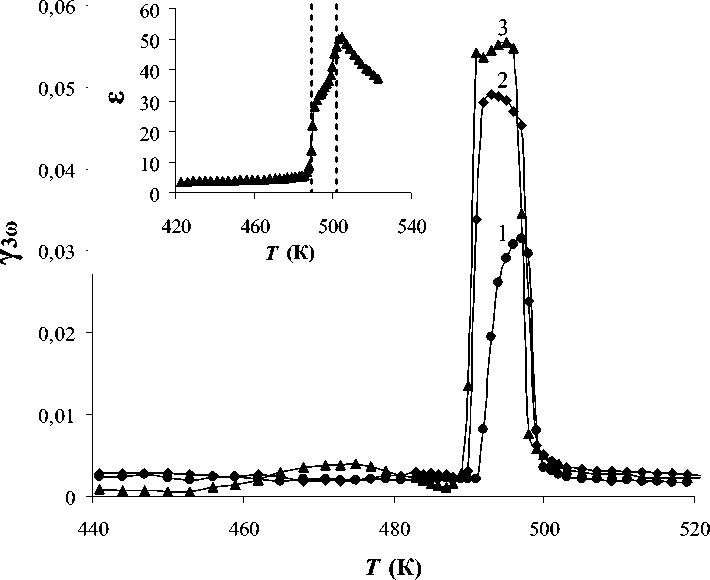
Рис. 4. Температурные зависимости коэффициента третьей гармоники Y _{3 o} PbZrO 3 при напряженностях модулирующего поля100 В/см (1), 200 В/см (2) и 400 В/см (3).

На вставке показана температурная зависимость диэлектрической проницаемости Е на частоте 100 кГ ц

ратуры для сегнетоэлектриков первого и второго рода. Результаты метода НДС для антисегнетоэлектрика PbZrO₃ показывают, что аномалия коэффициента у _{3 ю} наблюдается только в узком температурном интервале, соответствующем формированию промежуточной сегнетоэлектрической структуры. Аномалий коэффициента третьей гармоники в антисегнетоэлектрической фазе не наблюдалось.

Работа выполнена при поддержке Минобрнауки РФ (проект № 2014/424).