Метод обнаружения контуров на основе весовой модели изображения

В настоящее время практически во все сферы человеческой деятельности внедряются технологии компьютерного зрения. При этом разрабатываются новые эффективные методы обработки изображений для применения в конкретных приложениях. Среди других подходов активно развиваются модели и методы контурного анализа, которые используются в системах управления и навигации беспилотных транспортных средств [1], системах дистанционного зондирования Земли [2], системах обнаружения дефектов дорожного покрытия [3], биометрических системах [4] и др.

Модели контурного анализа относятся к среднему уровню представления изображений, на котором осуществляется обнаружение и описание признаков для их последующего анализа [5]. При обнаружении контуров определяются соответствующие им последовательности точек, а при описании – вычисляются характеристики этих последовательностей.

При решении задачи обнаружения контуров на изображении определяются границы – местоположения точек, в которых наблюдаются значительные изменения (перепады) яркости. Классические методы обнаружения границ базируются на операторах первой и второй производных, к которым относятся операторы Робертса, Собела, Превитт, Лапласа и др. Обнаружение контуров при использовании указанных операторов обычно осуществляется в три шага. На первом шаге выполняется сглаживание изображения для уменьшения шума, на втором – определяются границы, на третьем – из граничных точек отбираются точки контуров [6].

Помимо подхода на основе операторов производных, применяются морфологические методы. Изображения здесь рассматриваются как множества, а для их анализа применяются специальные операторы, такие как эрозия, дилатация, открытие и закрытие и др. Достоинством данных методов является высокая устойчивость к шуму [7,8].

Также развиваются методы на основе билатеральной фильтрации, которая позволяет учесть как яркостные, так и пространственные соотношения между точками изображения [9]. В отличие от многих других алгоритмов билатеральная фильтрация сохраняет информацию о границах, что позволяет на ее основе спроектировать эффективные детекторы контуров [10].

Кроме указанных подходов, предлагается и множество других, например, методы обнаружения контуров с использованием математического аппарата нечеткой логики [11, 12], методы на основе анализа независимых компонент [13], методы на основе модели случайного леса [14], вейвлетные методы [15] и др.

Согласно обзору, приведенному в работе [16], выделяют следующие классы методов обнаружения контуров: локальные методы (дифференциальные методы, статистические методы, методы фазовой конгруэнтности, методы порядковых статистик и морфологические методы, методы на основе комбинации локальных признаков), контекстуальные и глобальные методы (методы контурных особенностей, методы гельштальт-группировки, методы активных контуров), многомасштабные методы (методы анализа контуров в многомасштабном пространстве, методы фокусировки, методы локального контроля).

Несмотря на большое количество подходов к обнаружению контуров на изображениях, самым популярным методом решения этой задачи остается метод Кэнни [17]. Это метод стал фактическим эталоном, с которым сравниваются новые методы.

В данной работе предлагается новый метод обнаружения контуров, который можно отнести к классу многомасштабных методов. В его основе лежит анализ коэффициентов, полученных в результате вейвлет-преобразования. Реализация метода дает показатели точности и скорости, сопоставимые с соответствующими показателями детектора на основе метода Кэнни.

1.    Многомасштабные методы обнаружения контуров на основе вейвлет-преобразования

После широкого внедрения математического аппарата вейвлетов для анализа одномерных и двумерных функций появилось множество методов обработки изображений на его основе, в том числе предназначенных для обнаружения контуров. Привлекательность вейвлетов для решения рассматриваемой задачи связана с возможностью анализа набора изображений, полученных из исходного изображения и отличающихся детализированностью. Анализируемые изображения являются копиями друг друга, но имеют различное разрешение (масштаб). В общем случае набор масштабов может быть произвольным. Однако часто применяют вейвлет-преобразования с кратными масштабами (например, с масштабами 1, 2, 4, 8 и т.д., т.е. с масштабами, кратными 2).

Эффективность многомасштабных, в том числе вейвлетных, методов базируется на особенностях биологического зрения. Исследования в этой области показали сходство между зрением и многомасштабной обработкой изображений. Было признано, что рецептивные поля клеток зрительной коры млекопитающих можно охарактеризовать как пространственно локализованные, ориентированные и полосовые (селективные по структуре в различных пространственных масштабах). Поэтому желательно применение направленного многомасштабного разреженного представления.

Значительный вклад в развитие подходов к обнаружению контуров на основе вейвлет-преобразования был сделан Малла, Хвангом и Чжуном, которые показали, что локальные максимумы модуля вейвлет-преобразования позволяют обнаруживать местоположение нерегулярных структур на изображении [18, 19]. Они разработали подход с применением ориентированных вейвлетов, лежащий в основе большинства методов на основе вейвлет-преобразования [20,21].

К подходу Малла и др. близок подход на основе нечетных фильтров Габора, применение которых удовлетворяет критериям Кэнни для оптимальных детекторов границ [17]:

• 1)    хорошее обнаружение;

• 2)    хорошая локализация;

• 3)    только один отклик на одну границу.

2.    Весовая модель полутонового изображения

Данный подход предложен в работах Namuduri, Mehrotra, Ranganathan [22] и получил дальнейшее развитие в работе [23], где рассматривается многомасштабная техника выделения краев на основе нечетных фильтров Габора.

Развитие методов анализа сигналов и изображений на основе вейвлет-преобразования привело к созданию математического аппарата курвлетов. Возможности курвлет-преобразования позволяют построить на их основе эффективные методы обнаружения контуров. Например, в работах [24, 25] предлагается комбинированный подход, сочетающий курв-лет-преобразование и детектор Кэнни. Здесь на первом этапе вычисляются коэффициенты преобразования для нескольких масштабов и направлений. Затем формируется карта границ на основе анализа значений коэффициентов. Далее к карте границ применяются три основных шага традиционного оператора Кэнни: вычисление градиента, подавление немакси-мумов и двойная пороговая обработка. Результаты применения этого подхода показали очень хорошие возможности для обнаружения удлиненных ребер и также для генерации более замкнутых объектов, которые делают этот метод хорошей альтернативой для шага сегментации для любого дальнейшего алгоритма классификации на основе объектов.

Недостатком рассмотренных в данном параграфе подходов на основе вейвлет-преобразования является сравнительно большое время работы. Поэтому задача разработки новых методов обнаружения контуров на изображениях остается актуальной.

Дискретное вейвлет-преобразование раскладывает полутоновое изображение по базисным функциям, которые позволяют выявить его особенности в локальной области (определяется параметрами сдвига) при некотором масштабе (определяется параметром масштаба). В результате выполнения данного преобразования получают множества коэффициентов аппроксимации и детализации.

Для дискретного ортонормированного кратномасштабного вейвлет-преобразования полутонового изображения справедливо равенство сохранения энергии аналогичное равенству Парсеваля для преобразования Фурье:

N - 1 N - 1         2 j - 12 ^j 0 - 1

ZZ f k 2 1 = ZZ L j m,n + k = 0 1 = 0           m = 0 n = 0

J - 1 2 ^j - 12 ^j - 1                  J - 1 2 ^j - 12 ^j - 1

+ Z Z Z LH + Z Z Z HL mn +       (1)

j = jj m = 0 n = 0                j = jj m = 0 n = 0

J - 1 2 ^j - 12 ^j - 1

+ ZZZ HH 2mm,n , j = j 0 m = 0 n = 0

где f k l – значение яркости пикселя изображения в позиции ( k l ); LL j m n LH j m n HL j m n HH j m n – коэффициенты вейвлет-преобразования на уровне j в позиции ( m n ); j 0 – наименьший уровень разложения; J – число уровней разложения; N – размер изображений (изображение представляется в виде матрицы N х N ).

На основе равенства (1) можно построить модель в которой с каждым пикселем изображения будет ассоциирован вес – показатель его значимости для восприятия с точки зрения вклада в общую энергию. При этом представляется что наиболее значимыми являются пиксели в которых проявляются характерные особенности изображения. К таким особенностям например можно отнести перепады яркостей между областями изображения. Оценить величину перепада в некотором пикселе изображения можно с помощью соответствующих ему детализирующих вейвлет-коэффициентов. При этом энергия перепада будет пропорциональна евклидовой норме вектора данных коэффициентов.

В результате кратномасштабного ортонормирован-ного вейвлет-преобразования изображение представляется в виде матрицы аппроксимирующих коэффициентов и набора матриц детализирующих коэффициентов. Матрица аппроксимирующих коэффициентов представляет собой уменьшенную копию изображения а матрицы детализирующих коэффициентов содержат информацию необходимую для восстановления изображения из копии. При этом один пиксель изображения большего масштаба (копия меньших размеров) соответствует четырем пикселям изображения меньшего масштаба (копия больших размеров). Это предполагает что вес одного пикселя изображения большего масштаба входит в веса четырех пикселей изображения меньшего масштаба. Поэтому для выполнения энергетического равенства необходимо распределить указанный вес по четырем элементам.

Аппроксимирующие вейвлет-коэффициенты – это значения пикселей изображения наибольшего масштабного уровня (самой грубой копии). Это означает что соответствующие им значения энергии входят в значения энергии пикселей изображений остальных масштабов т.е. представляют собой начальные значения весов.

Таким образом получить веса (оценки энергии)

для каждого пикселя можно посредством выполнения следующих действий:

• 1.    Выполнить преобразование до уровня j 0 .

• 2.    Задать начальные значения весов:

  j 0 - 1, m , n

  
  

  ^LLj₀ ,m,n .

  
  

• 3.    Вычислить веса для всех уровней:

• 4.    Присвоить веса пикселям изображения:

w 2,m,n = ¹ w 2 - 1, m , n +

+ LH m /2, n /2 + HL} , m /2, n /2 + HH j^ /2, n /2 .

c ( f k , 1 ) = W 211 = w J , k , 1 .

Полученные веса сохраняют энергетическое равенство (1):

N - 1 N - 1         N - 1 N - 1

ZZ / 2 1 = ZZ w 21. .

k = 0 1 = 0          k = 0 1 = 0

Рассмотренная модель определена для ортонорми-рованных кратномасштабных вейвлет-преобразований и может быть обобщена для ортогональных кратномасштабных вейвлет-преобразований. В этом случае равенства (2) и (3) преобразуются в равенства (6) и (7):

W 2 - 1, m , n = K‘ 0 - 1 ^L L j , m , n ;

j,m,n     ^^j ^vvj - 1, m , n ¹

+ K j "( LH 2, m /2, n /2

^{+ H} L j , m /2, n /2 ^{+ HH}jmm /2, n /2 ) ,

где K j и K j - нормировочные множители.

Дальнейшее обобщение связано с тем, что нормировочные множители в формулах (6) и (7) можно рассматривать в качестве настроечных коэффициентов, значения которых определяются для решения конкретных задач.

Для решения задачи обнаружения контуров на изображении наиболее значимыми полагаются пиксели, в которых существенно меняется значение яркости. Величину перепада яркости в пикселе можно приближенно оценить с помощью детализирующих коэффициентов вейвлет-преобразования:

A f « V LH ² + HL¹ + HH ²,

где A f — величина перепада яркости в пикселе; LH , HL , HH – суммы всех нормированных детализирующих горизонтальных, вертикальных и диагональных коэффициентов различных уровней вейвлет-преобразования, соответствующих пикселю. Тогда в рамках рассмотренной модели можно вычислить веса, отражающие значимость пикселей с точки зрения величин перепадов яркости в них. Для этого достаточно в формуле (6) нормировочный коэффициент K j ₀ , положить равным нулю.

Отметим также, что при применении весовой модели для решения конкретных задач значения весов можно приводить к требуемому диапазону, например, к целочисленному интервалу от 0 до 255 для визуализации.

Весовая модель может быть представлена как результат преобразования исходного изображения в изображение, в котором атрибутами пикселей являются веса. Результат преобразования называется весовым изображением.

На рис. 1 а и б показаны полутоновое и соответствующее ему весовое изображение. Исходное изображение представляет собой стандартное тестовое изображение house размера 512 x 512 из коллекции USC-SIPI [26]. Для его преобразования использовалось ортогональное кратномасштабное вейвлет-преобразование Хаара, задаваемое выражениями:

LL j - 1, m , n ^- 4[ LL j ,2 m ,2 n +

⁺ LL j ,2 m + 1,2 n ⁺ LL j,2 m ,2 n + 1 ⁺ LL j ,2 m + 1,2 n + 1 ],

LH j - 1, m , n ^- 4[ LL j,2m ,2 n ⁺

⁺ LL j ,2 m + 1,2 n LL j ,2 m ,2 n + 1 " LL j ,2 m + 1,2 n + 1

HL j - 1, m , n ^— 4[ LL j ,2 m ,2 n

" LL j ,2 m + 1,2 n ⁺ LL j ,2 m ,2 n + 1 " LL j ,2 m + 1,2 n + 1

HH j - 1, m , n ^- ~[ LL j ,2 m ,2 n ^-

^- LL j ,2 m + 1,2 n ^- LL j ,2 m ,2 n + 1 ⁺ LL j ,2 m + 1,2 n + 1

Вычисления осуществлялись на основе описанной процедуры с применением формул (6) и (7). При этом количество уровней разложения было задано равным 9, а начальное значение было положено равным ну- лю, т.е. значения аппроксимирующих коэффициентов LLj0 ,m,n не использовались.

Как можно увидеть на рис. 1 а и б, границы на весовом изображении подчеркнуты сильнее по сравнению с исходным изображением.

Однако следует также отметить и недостаток весовой модели изображения. Он заключается в том, что веса пикселей в каждом блоке из четырех пикселей будут иметь одни и те же значения. Снизить влияние этого недостатка можно за счет дополнительной постобработки весового изображения.

3.    Детектор контуров на основе весовой модели изображения

Как уже было сказано выше, фактическим эталоном для алгоритмов обнаружения контуров на изображениях является детектор Кэнни. Процедура обнаружения контуров по методу Кэнни заключается в выполнении следующих шагов:

• 1.    Сглаживание изображения для уменьшения шума.

• 2.    Вычисление модуля и направления градиента для каждого пикселя изображения.

• 3.    Определение локально максимальных по модулю градиента пикселей (подавление немак-симумов).

• 4.    Пороговое преобразование с гистеризисом (с двойным порогом) градиентного изображения.

• 5.    Анализ связности граничных пикселей.

Пример работы детектора Кэнни для изображения на рис. 1 а показан на рис. 2. Здесь использовались значения нижнего и верхнего порогов 20 и 60 соответственно (значения яркости на изображении находятся в диапазоне от 0 до 255).

а)

Рис. 1. Весовая модель стандартного изображения «house»

Рис. 2. Обнаружение контуров детектором Кэнни на стандартном изображении «house»

Схему детектора Кэнни можно модифицировать на основе применения весовой модели изображения. Соответствующая процедура будет заключаться в последовательном выполнении следующих действий:

• 1.    Построение весовой модели изображения.

• 2.    Определение направлений линейных сегментов на весовом изображении.

• 3.    Анализ значимости пикселей.

• 4.    Связывание значимых пикселей.

На первом шаге осуществляется преобразование исходного изображения в весовую форму посредством описанной в предыдущем параграфе процедуры. На втором шаге определяются направления гра- ниц в пикселях весового изображения. На третьем шаге анализируется значимость каждого пикселя по сравнению с ближайшими соседями вдоль нормали к направлению границы в данном пикселе. На четвертом шаге найденные значимые пиксели связываются в контуры.

Основная проблема в реализации предложенного детектора заключается в определении направлений границ в пикселях весового изображения. Это связано с тем, что кратномасштабные вейвлеты не обеспечивают хорошей селективности направления [27]. Повысить направленную избирательность можно с помощью применения комплексного вейвлет-преобра-зования. Однако оно не получило широкого применения из-за трудностей, связанных с обеспечением свойств реконструкции и фильтрации. Затем было разработано комплексное вейвлет-преобразование двойного дерева DT-СWT. Данное преобразование обеспечивает (почти) совершенную реконструкцию, приближенную инвариантность сдвига, шесть направленных избирательностей, ограниченную избыточность и сравнительно эффективное время вычисления. Преобразование DT-СWT связывает между собой два кратномасштабных вейвлет-преобразования, за счет чего и определяется ограниченное количество направлений. Однако преобразование DW-CWT является более медленным относительно вещественных кратномасштабных вейвлет-преобразований, в том числе по сравнению с ортогональным преобразованием Хаара.

Для решения указанной проблемы можно воспользоваться фильтрами направлений с ядрами свертки размерами 3 x 3, 5 x 5, 7 x 7, 9 x 9 и т.д., например:

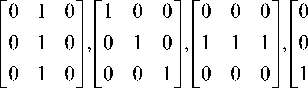
На рис. 3 показан пример работы предлагаемого детектора контуров на основе весовой модели для исходного изображения на рис. 1 а . При реализации детектора при построении весовой модели изображение было предварительно сглажено медианным фильтром, а перед определением направлений весовое изображение было обработано усредняющим box-фильтром. Применение указанных фильтров связано с использованием преобразования Хаара (9), которое может вносить искажения на границах областей.

Рис. 3. Обнаружение контуров на основе весовой модели на стандартном изображении «house»

По результатам проведенных экспериментов можно сделать вывод о том, что предлагаемый детектор по сравнению с детектором Кэнни дает более зашумленные контуры. Однако при этом он позволяет получить значимые детали, необходимые для описания изображения с целью последующей обработки для анализа, например, при решении задачи распознавания. Дополнительные иллюстрации работы детектора приведены на рис. 4, где на рис. 4 а и 5 а показаны исходные изображения «cameraman» и «jetplane» соответственно, а на рис. 4 б и 5 б – их контурные изображения.

Рис. 4. Обнаружение контуров на основе весовой модели на стандартном изображении «cameraman»

Достоинством предложенного подхода к обнаружению контуров является высокая скорость работы детектора. В табл. 1 приведены средние значения времени работы детектора Кэнни и детектора на основе весовой модели для стандартных полутоновых изображений размера 512 x 512. Эксперименты про- водились на компьютере со следующими характеристиками: 4 процессора AMD A8-7410 APU with AMD Radeon R5 Graphis, ОЗУ объемом 8 Гб, операционная система Microsoft Windows 10. Среднее время работы детектора Кэнни составляет около 0,9 с, а детектора на основе весовой модели –0,2 с.

а)

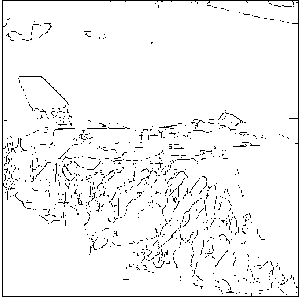
Рис. 5. Обнаружение контуров на основе весовой модели на стандартном изображении «jetplane»

Также в табл. 1 приведены количественные оценки различия контурных изображений, полученных предложенным методом и детектором Кэнни. В качестве мер различия выбраны известные критерии RMS (среднеквадратическая ошибка) и D Ku (расстояние Кульбака–Лейблера):

N - 1 M - 1

RMS = J 777 ZZ ( 1 1 ( i , j ) — 1 2 ( i , j ) ) 2 ,        (H)

у NM i = 0 j = 0

( 1 1 ( i , j ) + e ) ( 1 2 ( i , j ) + e )

D Ku

N - 1 M - 1

EZ( 11( i, j)-12( i ,j) ln i=0 j=0

NM

сти является бинаризация весового изображения для получения связных областей в виде «толстых» контуров. Соответствующие примеры приведены на рис. 6, где показано выделение областей значимости на изображениях «house» (рис. 6 а ), «cameraman» (рис. 6 б ) и «jetplane» (рис. 6 в ) с помощью пороговой обработки нормализованных весовых изображений (веса были приведены к диапазону от 0 до 255) с пороговыми значениями, равными 30. На основе данного детектора, добавив операцию утончения, можно построить процедуру выделения контуров, пример результата выполнения которой показан на рис. 7. В табл. 2 приведено время его работы.

где N , M – количество строк и столбцов; I 1 ( i , j ), I 2 ( i , j ) – пиксели первого и второго сравниваемых изображений в i -й строке и j -м столбце; £ - величина, обеспечивающая вычисление расстояния Кульбака– Лейблера при наличии нулевых пикселей. Величины в табл. 1 получены после приведения пикселей контурных изображений к значениям 0 и 1. При вычислении расстояния D Ku величина £ была принята равной 0,001. Это позволило определить, что наибольшие значения расстояний по критериям RMS и D Ku могут быть равны 1 и 6,909 соответственно. В среднем, различия между контурными изображениями, полученными предложенным методом и детектором Кэнни, не превышают 35 % и 13 % от максимально возможных значений по указанным критериям.

Таким образом, предлагаемый подход позволяет обрабатывать изображения более чем в 4 раза быстрее по сравнению с детектором Кэнни.

При решении различных задач актуально обнаружение значимых областей на изображениях. Значимые области содержат основную информацию, необходимую для последующего анализа изображений. Например, области значимости могут содержать окрестности контурных точек, т.е. фрагменты изображений, в пределах которых существенно изменяется яркость (в отличие от областей преимущественно однородной яркости). Рассмотрим детектор, в котором осуществляется преобразование изображения в весовую форму, анализ весов и формирование бинарной маски. Простейшим вариантом анализа значимо-

Табл. 1. Время работы детектора Кэнни и детектора на основе весовой модели

Изображения	Время работы детектора, мс		Расстояние
	Кэнни	На основе весовой модели	RMS	D Ku
boat	930	189	0,344	0,819
cameraman	910	191	0,274	0,518
house	880	189	0,206	0,293
jetplane	915	195	0,295	0,602
lake	891	190	0,351	0,853
livingroom	978	211	0,374	0,964
mandril	915	190	0,481	1,595
walkbridge	924	198	0,467	1,504

Табл. 2. Время работы детектора значимых областей на основе весовой модели

Изображения	Время работы детектора, мс
	без утончения	с утончением
boat	59	198
cameraman	55	248
house	55	163
jetplane	67	222
lake	53	223
livingroom	56	193
mandril	53	203
walkbridge	59	191

а)

б)

Рис. 6. Детектирование областей значимости

Заключение

Предложенный подход к выделению контуров на основе весовой модели позволяет обеспечить высокую скорость обработки изображений, превышающую скорость эталонного подхода на основе детектора Кэнни.

Применение весовой модели позволяет также построить детектор, который обеспечивает обнаружение на изображении наиболее значимых фрагментов.

Применение описанной техники может быть эффективно использовано в системах обработки информации и управления на основе методов и средств компьютерного зрения.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения научно-исследовательских работ по Государственному заданию № 2.1724.2017/4.6.

Рис. 7. Утончение изображения на рис. 6а