Метод обнаружения на основе посимвольного перемножения реализаций спектра наблюдаемого процесса с автоматическим расчетом порога принятия решения

В настоящее время все более широкое применение находят датчики автоматического срабатывания по контрольному радиосигналу от управляющего устройства. Важнейшим их параметром является дальность действия, определяемая мощностью принимаемого излучения и чувствительностью самого датчика. Повышение мощности в ряде случаев не всегда является приемлемым выходом, т. к. он связан с ростом энергопотребления управляющими устройствами. Поэтому более рациональным видится увеличение дальности работы датчиков за счет улучшения чувствительности приема. Очевидно, что здесь значительную роль играет метод обработки радиосигналов, положенный в основу работы датчиков. А поскольку обработка подразумевает в первую очередь решение задачи обнаружения радиосигнала, то целесообразно исследовать возможность увеличения дальности приема за счет применения рациональных подходов к их обработке.

Необходимо отметить, что аналогичные задачи приходится решать и в других областях приборного анализа, непосредственно связанного с обработкой нестационарных процессов. Указанные обстоятельства подчеркивают актуальность рассматриваемой проблематики.

ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ

С точки зрения статистической теории обработки сигналов основу задачи синтеза алгоритмов автоматического обнаружения при конечном времени наблюдения на фоне помех составляет выбор порога принятия решения. Действительно, с одной стороны, желательно не допустить пропуск сигналов, а с другой — минимизировать вероятность ложной тревоги, т.е. холостого срабатывания системы. Для радиоканалов выбор порога, обеспечивающего подобный компромисс, связан с определенными трудностями, обусловленными априорной неопределенностью характера помехового фона, а также отсутствием точных данных о параметрах обнаруживаемого излучения в мультиаль-тернативных системах, работающих с различными классами контрольных сигналов. Еще сложнее найти компромиссное решение при выборе порога в задачах масс-спектрометрии и хроматографии, связанных исключительно с обработкой нестационарных процессов.

В теории статистической радиотехники задача обнаружения сигнала $ ( t ) на фоне помех £ ( t ) подразумевает определение алгоритма, обеспечивающего принятие решения о наличии сигнала или его отсутствии в наблюдаемом процессе x ( t ) = $ ( t ) © £ ( t ), где символ © означает произвольное взаимодействие помехи с сигналом [1]. В этом случае процесс принятия решения представляется как совокупность операций сравнения некоторой статистической гипотезы о наличии сигнала в принятой выборке H 1 : x ( t ) = $ ( t ) © ^ ( t ) с ее альтернативой H ₀ : x ( t ) = £ ( t ), осуществляемых в соответствии с критерием, определяемым конкретными условиями. В частности для мульти-альтернативных систем целесообразен выбор критерия максимального правдоподобия (МП) в связи со сложностью определения матрицы потерь, а следовательно, величины условного риска [2].

Для критерия МП алгоритм принятия решения состоит в выборе наибольшей из величин функции правдоподобия to ₀ ( x | H ₀ ) и to 1 ( x | H 1 ) . Практическая реализация указанного алгоритма сводится к вычислению решающей функции Ф ( x ), заданной на выборочном пространстве X :

Ф ( x ) =

1, x е X 1

0, x е X ₀ ^,

где X । — область принятия гипотезы H 1 ; X ₀ — область принятия гипотезы H ₀ .

Согласно [1], решающая функция (1) соответствует нерандомизированному алгоритму, для которого вероятность необнаружения а (пропуск сигнала, или ошибка первого рода) рассчитывается как а = mi{ф(x| Hо)}, а вероятность ложной тревоги в (ошибка второго рода)

в = 1 - m i { Ф ( x| H i ) } , где m 1 {} — функция условных средних (статистический начальный момент первого порядка).

Решение алгоритма (1) связано с поиском компромисса между значениями а и в , поскольку снижение критической области отклонения гипотезы H ₁ неизбежно ведет к увеличению допустимой области принятия гипотезы H ₀ , и, следовательно, ухудшению его чувствительности в отношении ошибок второго рода.

Доминирующим этапом при реализации любого критерия, в том числе и МП, является выбор порога принятия решения G , разбивающего пространство допустимых значений на непересекаю-щиеся области X 1 и X ₀. Если для состояний s 1 (наличие) и s ₀ (отсутствие сигнала в принятой реализации x ( t )) априорно известны законы их распределения w_t ( x 1 ,..., xi |s 1 ) и w_t ( x 1 ,..., xi|s ₀), то затруднений в расчете значения G не возникает. Однако на практике сложно обеспечить указанные условия. В частности, нестационарность исходного обрабатываемого материала в масс-спектрометрии практически исключает возможность получения контрольной выборки, однозначно характеризующей фоновое излучение. Следовательно, возникает проблема определения порога принятия решения. Таким образом, задача данной работы состоит в разработке метода, обеспечивающего автоматический расчет порога принятия решения при обнаружении сигналов с низкой энергетикой в условиях отсутствия априорных знаний о характере шумов.

ОБОСНОВАНИЕ ЭТАПОВ МЕТОДА РАСЧЕТА ПОРОГА ПРИНЯТИЯ РЕШЕНИЯ

ДЛЯ СИГНАЛОВ С НИЗКОЙ ЭНЕРГЕТИКОЙ

В [2] обоснован следующий подход для крите- рия МП по выбору порога принятия решения при разделении областей X 1 и X0:

m 1 { x 1 ,..., x„ |s 1 } + m 1 { x 1 ,..., xn |s о }

В традиционных обнаружителях уровень порога, как правило, устанавливается вручную оператором, исходя из априорных сведений об энергетике контрольных сигналов. Но в этом случае необходимо, чтобы их спектральная мощность существенно превышала уровень шумового фона. Это накладывает на мультиальтернативные системы дополнительные ограничения — увеличение энергопотребления или же существенное сокращение радиуса зоны обслуживания, что не всегда приемлемо. Действительно, для реализации условия (2) необходимы достоверные сведения хотя бы об одной из выборок, однозначно характеризующих какую-либо из гипотез H ₁ или H ₀ . Но в ряде случаев уровень сигнала источника тревог бывает непостоянным, например в системах слежения, и его мощность, определяемая различными факторами среды распространения (канала связи), может выходить за пределы области устойчивого срабатывания выбранного порога обнаружения. Это же касается и задач электронной спектрометрии, когда рамки изменения конечного результата (полезного излучения) точно не определены.

В связи с этим первый этап рассматриваемой методики направлен на обеспечение условий выделения сигнала на фоне шумов. Для этого предлагается последовательно осуществлять поэлементное перемножение спектральных образов принятых реализаций

N

F © F ² © .... © F n = П ( F ) n . (3) n = 1

В выражении (3) F in — преобразование Фурье от дискретизированного наблюдаемого потока x ( t ); n — текущее значение дискретизированной реализации x ( t ); N — общее число реализаций.

Продуктивность предложенного этапа объясняется следующим. Поскольку спектральные составляющие шумовой компоненты наблюдаемого входного потока не коррелированны от реализации к реализации, то в результирующем спектральном образе (3) их номинальное значение будет асимптотически с увеличением N стремиться к (m1 {fF})N, где m^F^i} — медианное значение спектра наблюдаемого потока x(t) = £(t). Если же при этом (m1{fF})<(m 1 Uy j). где Fsi — преобразование Фурье от x(t) = s(t) © ^ (t), то, начиная с некоторого N , обеспечится однозначное выде- ление сигнала на фоне помех. Такой подход позволит работать с сигналами, энергетика которых сопоставима и даже ниже уровня шумового фона, что особенно важно в решении задач приборного анализа.

На втором этапе осуществляется расчет порога принятия решения. При реализации автоматов желательно, чтобы порог не задавался извне, а рассчитывался исходя из параметров наблюдаемого потока без предварительного обучения. Для этого предлагается предварительно рассчитать порог G 0 для использования его в качестве порога разбиения входной реализации в спектральном представлении на области X ₁ и X ₀ (соображения по выбору формулы расчета G 0 приведены в следующем разделе). Далее для каждой из них строить распределения w_i ( x ₁, ..., x_i s ₁) и w_i ( x ₁, ..., x_i s ₀) , считая что значения выборки, превысившие порог разбиения, являются только сигнальными компонентами. И уж затем рассчитать порог G принятия решения по критерию МП, согласно выражению (2). Данная формула также требует уточнения, поскольку ее достоверность, как показали проведенные исследования, обеспечивается при выполнении в общем случае следующего условия:

0.5 <

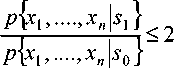
где p {} — среднее квадратичное отклонение.

Третий этап методики заключается в непосредственном принятии решения о наличии или отсутствии сигнала в наблюдаемой выборке. С целью исключения срабатывания устройства по случайным шумовым всплескам предлагается окончательное решение принимать только при наличии в спектре интервала непрерывности из компонент, превысивших значение G , длиной не менее k , где величина k определяется минимальной шириной спектра обнаруживаемых сигналов. Такое допущение правомерно в силу того, что единичный спектральный всплеск, превысивший порог может являться шумовым, в то время как вероятность такого выброса сразу k рядом расположенных частотных компонент для шума очень мала [4].

ОСНОВНЫЕ РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА

В эксперименте моделировался тракт приема с полосой пропускания A F = 10 кГц. В качестве контрольного сигнала — радиоимпульс на поднесущей частоте f ₀ = 2.5 кГц с эффективной шириной спектра A f s = 80 Гц при значениях отношения сигнал/шум (ОСШ) 0.8–0.9 дБ. Здесь ОСШ измерялось как отношение спектральной мощности сигнала к спектральной плотности шума. Длительность одной реализации наблюдаемой выборки составила 512 отсчетов. На рис. 1 представлен спектр входной реализации. Для удобства отображения результатов, здесь и в последующем все представленные значения A ( f ) нормированы относительно максимума.

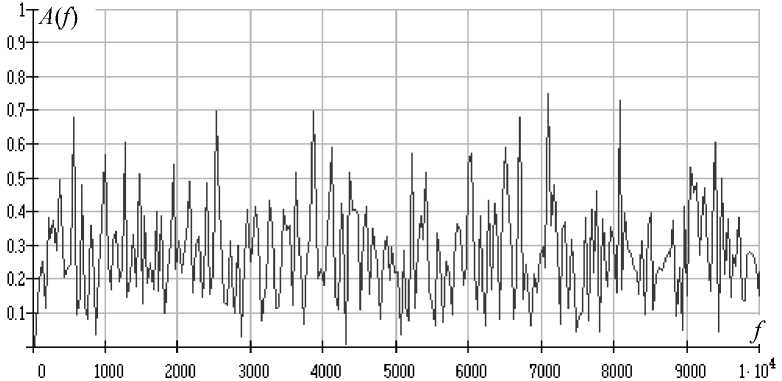
Рис. 1. Спектр первичной реализации наблюдаемого входного потока

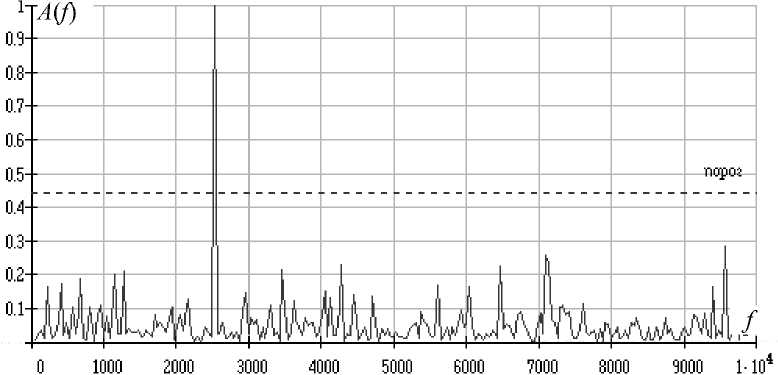
Рис. 2. Результирующий спектр после посимвольного перемножения трех реализаций наблюдаемого входного потока

Стоит отметить, что для указанных условий реализация всего лишь трех операций в соответствии с формулой (3) позволила обеспечить однозначное выделение сигнала на фоне помех (рис. 2). Таким образом, общая длительность наблюдаемого потока, необходимая для достоверного выделения сигнала, составила 3 • 512/ f д ; где f д — частота дискретизации.

На рис. 2 показан порог G принятия решения, автоматически рассчитываемый в ходе реализации процедуры обнаружения.

Поиск величин, способных выступать в качестве расчетных предварительных значений G ₀ для порога разбиения, показал целесообразность выбора различных комбинаций первого начального m_i {} и второго центрального момента m ₂ {} от наблюдаемого входного потока [3]. Основным требованием, предъявляемым к порогам, являлась максимизация вероятности правильного распознавания при минимизации ложной тревоги. Так, в табл. 1 представлены значения потенциальных порогов разбиения при различных ОСШ (ОСШ рассчитывалось в полосе обнаружения), полученных в ходе предварительных исследований. В качестве порога разбиения G 0 применялись следующие расчетные величины:

G i = m i { x ( t ) } + p { x ( t ) } , G ₂ = 2 • m i { x ( t ) } + p { x ( t ) } ,

G з = 3 • m i { x ( t ) } , G 4 = 2 • m i { x ( t ) } ,

G ₅ = m _i { x ( t ) } + m 2 { x ( t ) } , G 6 = m ₂ { x ( t ) } .

Дополнительные условия по выбору порога определялись, исходя из следующих соображений.

• •    Принятие решения осуществляется только

по совокупности тех реализаций, которые использовались для расчета порога (в эксперименте по трем), т. е. без наличия дополнительной контрольной выборки.

• •    Обеспечение устойчивой работы автомата как при низких, так и высоких значениях ОСШ.

• •    Независимость от диапазона разброса сигналов по амплитуде в полосе обнаружения.

• •    Возможность применения как в мультиаль-тернативных, так и в системах, работающих только по одному контрольному сигналу.

Совокупным требованиям в наибольшей степени соответствовало значение G ₃ , которое и было выбрано в качестве порога (рис. 2). В частности, в табл. 2 представлена зависимость ошибок второго рода для порога разбиения G ₃ при различных ОСШ.

Табл. 1. Значения предварительно рассчитанных порогов разбиения G ₀ в зависимости от ОСШ

Вид порога разбиения	Значение ОСШ, дБ
	20	15	10	5	0	-5
"Идеальный"	506	390	305	232	195	170
G 1	525	302	226	137	112	74
G 2	782	461	356	212	186	108
G 3	772	476	380	257	222	167
G 4	515	317	254	171	148	126
G 5	7414	2216	1181	349	212	183
G 6	7150	2057	1054	263	143	117

Табл. 2. Значения ошибок второго рода β для G 3 в зависимости от ОСШ

Значение ОСШ, дБ	Значения β
22	0.027
20	0.021
18	0.019
16	0.014
14	0.009
12	0.007
10	0.004
8	0.002
6	0.0008

Во избежание срабатывания устройств обнаружения по случайным шумовым выбросам предложено в реализационных алгоритмах на этапе принятия решения учитывать дополнительное условие — наличие не менее трех последовательно расположенных спектральных компонент, превысивших порог, т.е. k =3.

Необходимо отметить, что значение G ₃ , используемое в эксперименте, в общем случае не является оптимальным. Вполне вероятно, что для других условий и классов сигналов целесообразен выбор в качестве порога другого значения. В частности, если ОСШ в полосе обнаружения не хуже 20 дБ, то лучшие результаты по показателю β у порога G ₄ . Напротив, если ОСШ менее 1–2 дБ, то предпочтение стоит отдать G ₅ и G ₆ . Поэтому, данный вопрос требует проведения дополнительных исследований.

ЗАКЛЮЧЕНИЕ

Предложенный метод открывает универсальный подход к анализу нестационарных процессов, причем не только в автоматах обнаружения. Он вполне применим и к билинейным распределе- ниям, а следовательно, его приложение в этой области может значительно расширить возможности технического анализа и процедур измерения частотно-временных параметров. В частности, в совокупности с методами, представленными в [5], а также методом Саукова [6] он значительно может повысить продуктивность операций распознавания. Дальнейшее развитие данного направления видится в совершенствовании на его основе процедур обнаружения шумоподобных процессов, а также оптимизации алгоритмов выбора порога принятия решения.