Метод обратного преобразования для анализа временных рядов

Введение. Можно сказать, что для специалистов, занимающихся анализом данных, в большинстве случаев прогнозирование является основной целью и задачей. Современные методы статистического прогнозирования зачастую способны с достаточно высокой точностью спрогнозировать практически любые возможные показатели [1].

Прогнозирование – система научно обоснованных представлений о возможных состояниях объекта в будущем и альтернативных путях его развития [2]. Не существует универсальных методов прогнозирования на все случаи жизни. Любая практическая задача прогнозирования может быть удовлетворительно решена лишь ограниченным числом методов [3]. Выбор метода прогнозирования и его эффективность зависят от множества условий: от цели прогноза, периода его упреждения, уровня детализации и наличия исходной информации [4]. Наиболее часто применяемым методом прогнозирования является математическое моделирование. Математическая модель – приближенное описание определенного процесса или явления внешнего мира, выраженное с помощью математического аппарата [5].

Составляющие временного ряда. Часто при исследовании временного (динамического) ряда его изображают в виде следующей математической модели:

Y = Y + E, где: Yt - значение временного ряда; Yt - систематическая (детерминированная) составляющая временного ряда; Et - случайная составляющая временного ряда [6].

Систематическая составляющая временного ряда Y t является результатом влияния на анализируемый процесс постоянно действующих факторов. Можно выделить две основные систематические составляющие временного ряда:

• 1)    тенденция временного ряда;

• 2)    циклические колебаний ряда.

Тенденция (тренд) представляет собой общую закономерность изменения показателей временного ряда, устойчивую и наблюдаемую в течение длительного периода времени. Тренд описывается с помощью некоторой функции, как правило, монотонной. Эту функцию называют функцией тренда, или просто – трендом [7].

Среди факторов, формирующих цикличность колебаний ряда, в свою очередь можно выделить две компоненты:

• 1)    сезонность;

• 2)    цикличность.

Сезонность представляет собой результат воздействия факторов, действующих с определенной, заранее известной периодичностью. Это регулярные колебания, носящие периодический характер и заканчивающиеся в течение года. Циклическая компонента – неслучайная функция, описывающая длительные (более года) периоды подъема и спада [8; 9].

Случайная составляющая временного ряда E t - это оставшаяся после выделения систематических компонент составная часть временного ряда. Она отражает воздействие многочисленных факторов случайного характера и представляет собой случайную, нерегулярную компоненту.

Случайные величины разнообразны по своей природе, происхождению, однако закон распределения можно записать в единообразной универсальной форме, а именно в виде функции распределения, одинаково пригодной как для дискретных, так и для непрерывных случайных величин [10].

Метод обратного преобразования. В целях прогнозирования, а также имитационного моделирования может возникнуть необходимость в методе генерации случайной компоненты временного ряда. Для этой цели воспользуемся методом обратного преобразования.

Пусть случайная величина X имеет функцию распределения F(x) . Примем, что F 1 (x) - это обратная функция F(x) . Тогда алгоритм для генерации случайной величины X с функцией распределения F(x) будет следующим:

• 1.    Генерируем величину U, имеющую равномерное распределение на промежутке (0;1).

• 2.  Возвращаем X=F¹(U).

На рис. 2 этот алгоритм изображен графически и случайная величина, соответствующая этой функции распределения, может принимать либо положительные, либо отрицательные значения. Это зависит от конкретного значения U . На рис. 1 случайное число U i в результате дает положительное значение случайной величины X i , тогда как случайное число U 2 в результате дает отрицательное значение случайной величины X 2 [II].

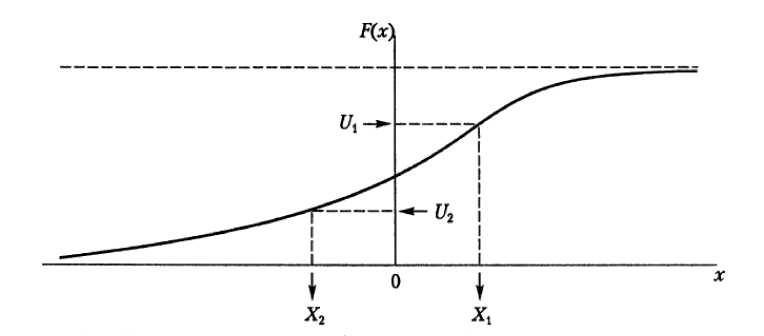
Рис. 1. Использование метода обратного преобразования для генерирования случайной величины

• Fig. 1.    Using the reverse conversion method to generate a random variable

Оценка функции распределения случайной величины. Рассмотрим наш временной ряд как последовательность x i , x i ,...X n независимых и одинаково распределенных, по определенному закону, случайных величин, которая называется выборкой объема n . Каждое x t (t=1, 2,...n) называется вариантой. Имея выборку, мы не имеем информации о виде функции распределения F(x) . Требуется построить оценку (приближение) для этой неизвестной функции.

Наиболее предпочтительной оценкой функции F(x) будет являться эмпирическая функция распределения F n (x) . Эмпирической функцией распределения (функцией распределения выборки) называют функцию F n (x) , определяющую для каждого значения x относительную частоту события X, т.е.

F_n ( x ) = n x ,

n где: nx – число значений xt, меньших x; n – объем выборки.

При достаточно большом объеме выборки функции F n (x) и F(x)=P(X мало отличаются друг от друга. Отличие эмпирической функции распределения от теоретической состоит в том, что теоретическая функция распределения определяет вероятность события X < x, а эмпирическая функция определяет относительную частоту этого же события [12].

Эмпирическая функция распределения обладает всеми свойствами интегральной функции распределения:

• 1)    значения эмпирической функции распределения принадлежат отрезку [0;1];

• 2)    F n (x) – неубывающая функция;

• 3)    F n (x)=0 при x <  x _miп, если x _min- наименьшая варианта; F_n(x)=1 при x > x _min, если x _min-наибольшая варианта [6].

Однако для использования метода обратного преобразования удобно иметь непрерывную функцию распределения, поэтому необходимо интерполировать полученную эмпирическую функцию.

Построение прогнозной модели. Приведем пример использования метода обратного преобразования при построении прогнозной модели. В качестве исходных данных используем среднемесячные показатели электропотребление на территории Красноярского края за 3 года с января 2009 г. по декабрь 2011 г. [13].

С помощью некоторой регрессионной модели были рассчитаны прогнозные значения временного ряда. Фактические Y t и прогнозные Y значения временного ряда представлены в табл. 1.

Таблица 1

t	Yt	Yt	t	Yt	Yt	t	Yt	Yt	t	Yt	Yt
1	51,0123	53,09764	11	35,5809	43,42324	21	37,8690	44,58914	31	17,1468	15,15964
2	38,2345	38,37535	12	53,2584	54,26158	22	63,4957	57,61664	32	20,8548	21,45395
3	40,0023	35,24303	13	52,3887	52,69219	23	72,9843	72,28322	33	29,3791	31,55531
4	25,1288	32,13879	14	39,9125	41,30390	24	88,0214	83,09426	34	51,1710	44,09931
5	22,9338	27,08163	15	39,2113	32,14284	25	82,6095	79,01463	35	61,5869	59,79590
6	27,0146	20,64426	16	31,3420	24,38189	26	62,7282	63,15378	36	71,2594	73,02318
7	25,1154	17,77792	17	26,0102	19,52312	27	50,0250	48,20592
8	16,6987	19,20278	18	20,5578	17,87433	28	29,6211	34,02474
9	27,3114	23,86244	19	12,1214	22,62140	29	22,2954	22,75450
10	29,2400	31,48983	20	24,9374	32,44863	30	17,8092	15,25792

Фактические Y и прогнозные Y значения временного ряда

Построим эмпирическую функцию распределения значений отклонений e t прогнозных значений Y_t от фактических значений Y, временного ряда e_t = Y - Y . Для этого необходимо ранжировать выборку{ e t }, таким образом получив выборку { e > = { e _(1}<  е _(2}<... <  e ₍„J (табл. 2).

Ряд значений e и e

Таблица 2

t	e t	e ( t )	t	e t	e ( t )	t	e t	e ( t )	t	e t	e ( t )
1	–2,085	–10,500	11	–7,842	–2,085	21	–6,720	1,791	31	1,987	6,370
2	–0,141	–7,842	12	–1,003	–1,764	22	5,879	1,819	32	–0,599	6,487
3	4,759	–7,511	13	–0,303	–1,391	23	0,701	1,987	33	–2,176	6,960
4	–7,010	–7,010	14	–1,391	–1,003	24	4,927	2,551	34	7,072	7,068
5	–4,148	–6,720	15	7,068	–0,599	25	3,595	2,683	35	1,791	7,072
6	6,370	–4,404	16	6,960	–0,459	26	–0,426	3,449	36	–1,764	7,337
7	7,337	–4,148	17	6,487	–0,426	27	1,819	3,595
8	–2,504	–2,504	18	2,683	–0,303	28	–4,404	4,759
9	3,449	–2,250	19	–10,500	–0,141	29	–0,459	4,927
10	–2,250	–2,176	20	–7,511	0,701	30	2,551	5,879

Так как частота каждой вариации равна единице, эмпирическая функция будет иметь вид:

0, e ■      / , e^ ) ;

F n ( е ) =

t

n

e ^Е[ e ( t ) , e ( t + 1) ) ; t ^0,1,...^, n;

...;

J, e e[ e_ui), +» ).

График функции F n (e) представлен на рис. 2.

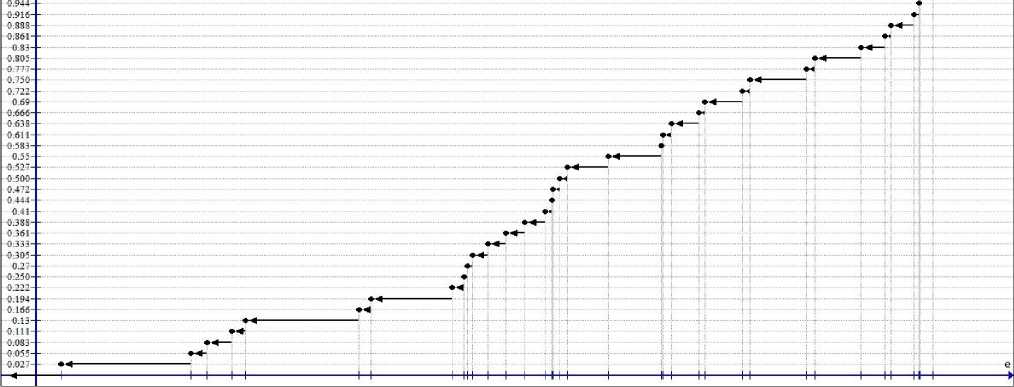
Рис. 2. График эмпирическая функция распределения F n (e)

• Fig. 2.    Graph of the empirical distribution function F n (e)

Полученная эмпирическая функция F n (e) имеет дискретный вид. Применим кусочнолинейную интерполяцию, чтобы получить непрерывную функцию распределения случайной величины F ^* ( e ). Для этого используем уравнение прямой, проходящей через две точки:

y = ( x - X 1 ) X

У 2 - У 1

+ У 1 .

Непрерывная функция распределения случайной величины F ^*( e ) будет иметь вид:

0,

e ■■ (     < ■ e (1) ) ;

..;

F n ( e ) H

⁽ e ' ^- e ( t ) ) ^X

к e ( t + 1)    e (

t - 1 + n - 1^,

e ^e[ e ( t ) , e ( t + 1) ) ; t = o,¹,-, n ;

...;

1,

e g[ e ( n) , w).

График функции F ^* ( e ) представлен на рис. 3.

*

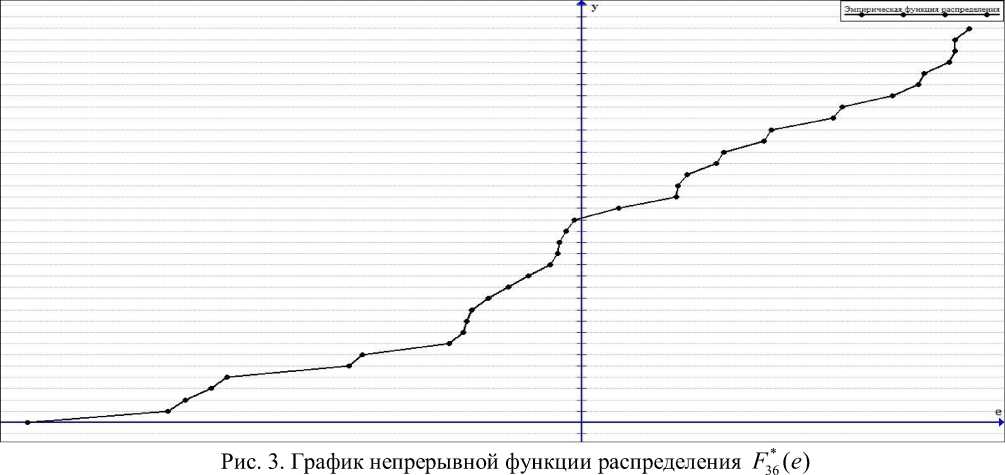
Fig. 3. Graph of the continuous distribution function F ( e )

Оценка прогнозной модели. Для дальнейшего анализа данного метода рассмотрим несколько моделей прогноза [14]:

• 1.    Значение временного ряда Y примем как полностью детерминированный процесс, для осуществления прогноза используем значения Y , рассчитанные при помощи регрессионной модели.

• 2.    Значение временного ряда Y примем как случайную величину, для которой построим функцию распределения F * ( e ) и осуществим расчет прогнозных значений Y_t ' .

• 3.    Значение временного ряда Y примем как совокупность значений Y , рассчитанных при помощи регрессионной модели и случайной компоненты e t , для которой построим функцию распределения F * (e ) и осуществим расчет прогнозных значений e\ .

Сделаем оперативный прогноз уровней электропотребления. Для этого исключим из рассмотрения последние 5 наблюдений из выборки и рассчитаем новые оценки параметров регрессионной модели, а также новые функции распределения F ^* ( x ) и F ^* ( e ).

Применим алгоритм обратного преобразования к полученным функциям F ^* ( x ) и F ^* ( e ). Для этого сгенерируем выборку {u t } случайных чисел, имеющих равномерное распределение в промежутке [0;1]. Возвращаем Yt = F * ^{- 1}( u_t ) и e't = F₃ *₁ ^{- 1}( u_t ). Результаты расчета представлены в табл. 3.

Таблица 3

Результаты применения алгоритма обратного преобразования

№	t	Y t	u t	et	Y + e ‘	Y'
1	32	25,1456	0,0608	–7,1360	18,0096	6,9693
2	33	37,1619	0,6514	1,9654	39,1274	14,9283
3	34	52,0351	0,6577	2,1085	54,1436	15,2489
4	35	70,5459	0,0515	–7,1507	63,3952	6,8725
5	36	86,8325	0,5448	0,3808	87,2133	13,4902

При рассмотрении полученных результатов видно, что сумма Y_t + e'_t лежит ближе к фактическим данным, чем прогнозные значения Y , рассчитанные при помощи регрессионной модели. Таким образом, спрогнозированные значения e ‘ в некоторой степени сгладили ошибку прогноза (рис. 4).

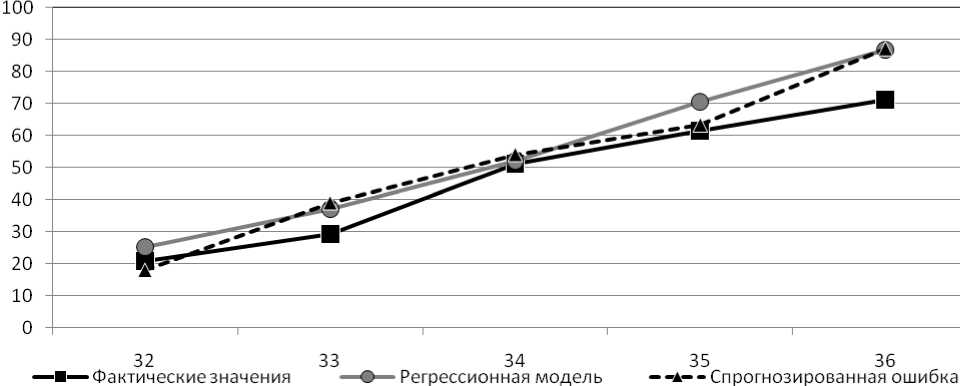
Рис. 4. Графическое отображение результатов прогноза

• Fig. 4. Graph displaying forecast results

Для критерия оценки качества модели определим значение средней ошибки аппроксимации, которую рассчитаем по формуле [15]:

n

A = ¹ Z n t = 1

( Y - Y np )

Y ф

x 100%,

где: Y пр – прогнозные значение временного ряда; Y ф – фактические значение временного ряда; n – размер временного ряда [10].

Значения средней ошибки аппроксимации для Y_t , Y_t’ и Y_t + e ‘ составляют:

• 1)    A ( Y ) « 17,03%;

• 2)    A ( Y ) « 71,18%;

• 3)    A ( Y + e ‘ ') ~ 15,59% .

Самый высокий показатель средней ошибки аппроксимации был получен при допущении, что временной ряд Y t является случайной величиной. Средняя ошибка аппроксимации для регрессионной модели меньше на 54,15 %. Это говорит нам, что временной ряд является детерминированной величиной. В результате включения в регрессию значений e‘ , средняя ошибка аппроксимации снизилась еще примерно на 1,44 %.

Заключение. Представленный выше метод может быть использован для определения непрерывной функции распределения случайной величины и генерации случайной величины в целях прогнозирования и имитационного моделирования.