Метод оценивания угла фазового сдвига и мгновенной частоты квазигармонических сигналов в режиме реального времени

Оценка параметров сигналов, близких к гармоническим, по конечной выборке является фундаментальной проблемой во многих приложениях, включая радиолокацию, гидролокацию, связь, акустику и оптику [1–4]. Задача определения полной фазы сигнала также возникает при исследовании синхронизации в сложных колебательных системах различной природы [5]. Сюда относятся, например, методы адаптивной глубокой стимуляции мозга [6], которые широко используются для лечения болезни Паркинсона и других неврологических расстройств. Для их эффективного применения требуется настройка параметров стимуляции в соответствии с фазой и амплитудой периферического или нейрофизиологического сигнала, вычисляемых в режиме реального времени [7]. Популярный подход к оценке нестационарной полной фазы и амплитуды заключается в использовании преобразования Гильберта или вейвлет-преобразования [8]. Однако эти методы плохо подходят для анализа в реальном времени, тогда как оперативная оценка полной фазы и амплитуды часто имеет решающее значение для управления сложными системами. Как правило, на основании информации о системе можно выдвинуть физически обоснованные предположения о модели сигнала, а также о скорости и диапазоне изменения его параметров.

Метод

Рассмотрим два квазигармонических сигнала с различными огибающими, полные фазы которых отличаются на постоянную величину ψ :

x1(t)=X1(t)cos(θ(t)), x2(t)=X2(t)cos(θ(t)+ψ),

удовлетворяющих физически обоснованному предположению о непрерывности, ограниченности амплитуд и мгновенной частоты ω ( t ) и всех их производных

d θ ( t )

0< ω m ≤ω ( t )= dt

0< X m ≤ X 1,2 ( t ) ≤ X M ,

d k ω ( t ) dt^k

d^kX 1,2 ( t ) dt^k

≤ ω ( t ) ω ^k B ,

≤ X 1,2 ( t ) ω kX ,

где k = 1, 2,…, ω m , ω M – границы возможных значений мгновенной частоты и ω B <  ω M , X m , X M – границы возможных значений амплитуд сигналов, ω B , ω X – максимальные частоты фазового и амплитудного спектра (причем ω X <  ω M ) соответственно. В работе [9] показано, что при выполнении условий (1) в силу теоремы Пэли–Винера функция θ ( t ) представима сходящимся на всей числовой оси рядом Тейлора и имеет финитный спектр, носитель Θ ( Ω ) которого принадлежит отрезку [– ω B , ω B ]:

ω B

θ ( t ) = ∫ Θ ( Ω )exp( i Ω t ) d Ω .

-ω B

В этом случае такое квазигармоническое представление является единственным, то есть полная фаза и амплитуда сигналов x 1 ( t ), x 2 ( t ) определены однозначно. Предположим, что полные фазы и огибающие отвечают следующим условиям медленности изменения [9, 10]:

го ( t ) = 0 ( t ) - ци ²( t ), X i - ц X i ( t ) го ( t ), X 2 — ц X 2 ( t ) го ( t ), 0 <  ц <  1.

Заметим, что условия медленного изменения параметров не накладывают ограничения на ширину спектра сигнала. Иными словами, сигнал может иметь широкий спектр за счет существенного, но медленного изменения мгновенной частоты и/или амплитуды.

Выберем временной интервал T , удовлетворяющий условию го T < п, и запишем значения сигналов в точках t , ( t – T ) и ( t – 2 T ):

%i (t - kT) = Xi cos(0 - к го T) + 51 (t - kT), x2(t -mT) = X2 cos(0 -mгоT + v) + 52(t -mT).

Здесь индексы k и m принимают значения 0, 1, 2; введены обозначения X 1 = X i ( t ), X 2 = X 2 ( t ), 0 = 0 ( t ) и го = го ( t ), а величины 5 1 ( t ) и 5 2 ( t ) являются отклонениями от гармонической модели, вызванными непостоянством частоты и амплитуд на временном интервале [ t –2 T , t ] и наличием аддитивного шума. Построим следующие произведения значений сигналов:

a km ( t ) = Х 1 ( t - kT ) x 2 ( t - mT ) =

= X i X 2 cos( 0 + (1 - k ) го T ) x                        (3)

x cos( 0 + (1 - m ) го T + v ) + a km ( t ).

Новые величины a _km ( t ) также являются погрешностями, которые обусловлены наличием исходных отклонений 5 1 ( t ), 5 ₂( t ) от модели гармонического сигнала.

Рассмотрим три сочетания произведений (3):

bi (t) = a02 (t) - a20 (t) ® 2X1 X2 sin(гoT) cos(гoT) sin(v) + ₽1 (t), b2 (t) = aoi (t) - a10 (t) + a12 (t) - a21 (t) ® 2X1 X2 sin(гoT) sin(v) + 02 (t),                                                      (4)

b3 (t) = 2an(t) - a02 (t) - aM (t) « 2X1X2 sin2(гoT) cos(v) + ₽3 (t), где введены следующие обозначения 01= a02( t )-a20( t), 02( t) = a01( t) - aw( t) + a12( t) - a21( t), 0з( t ) = 2an( t)- a02( t)- a20( t). Легко убедиться, что из этих сочетаний можно построить следующие оценки параметров сигнала:

~ 1 I ^( t ) 1

го = — arccos ----- ® го + 5_ш ( t ),

T        ^ b 2 ( t ) J

, | Ь2(t) • v = arctgl —-Sin(гo T) b(t)

= arctg

= v + 5 v ( t ).

Для того, чтобы иметь возможность получать оценку разности фаз в диапазоне [- п , п ], функцию arctg в выражении (6) нужно вычислять с учетом знаков b 2 ( t ) и b 3 ( t ).

Ошибка оценки частоты 5_Ш ( t ) имеет вид

-0 1 ( t ) + cos( гo T Щ t )

2 X 1 X 2 T sin²( гo T )sin( v ).

Из-за наличия в знаменателе синуса частоты и фазы наблюдается сингулярность этой ошибки на краях диапазона частот ( го = 0 и го = го / T ), а также при v = 0 и v = ±п . Ошибка оценки разности фаз определяется выражением:

5 v ( t ) =

- cos( гo T ) cos( v ) 0 1 ( T ) + cos( v ) 0 ₂ ( t ) - sin( гo T ) sin( v ) 0 ₃ ( t )

Видно, что в отличие от ошибки оценки частоты (7) сингулярности при v = 0 и v = ±п в выражении (6) не наблюдается, но ошибка оценки разности фаз (8) также растет на краях частотного диапазона. Численные эксперименты полностью подтверждают выражения (5 – 8).

Перейдем к реализации введенных оценок методами цифровой обработки сигналов. Пусть сигналы подвергнуты дискретизации с шагом А < п / го . Обозначим x [ n ]= x ( n А ) и предположим, что условия (2) выполняются на интервале [( n - L +1), n А ], где L = 2 Q + M . Параметр Q >  1 назовем коэффициентом прореживания. Он необходим в случае, когда частота дискретизации 2 п / А существенно превышает частоту сигналов, – об этом говорят погрешности (7) и (8). Параметр M >  1 имеет смысл количества усреднений при расчете сочетаний (4). Тогда произведения (3) примут следующий вид:

a km [ l ] = x 1 [ l - kQ ] x 2 [ l - mQ ] =

= X 1 X ₂ cos( 0 - го ( n - 1 + kQ ) А ) x x cos( 0 - го ( n - 1 + mQ ) A + v ) + a _km [ l ], l = n - M +1,..., n .

Здесь обозначено 0 = 0( n А). Суммируя эти произ- ведения по индексу l, получим:

ⁿ         MX ₁ X ₂

A km [ n ]= > , a km [ l ] =     x l = n - M + 1               ²

x cos(гo( k - m) Q А + v) +

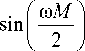
MX 1 X 2

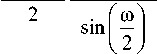
x cos( гo ( M - 1 + kQ + mQ ) А- 2 0-v ) + £ a km [ l ].

l = n - M + 1

Следует отметить, что A12[n] = A01[n – Q], A21[n] = A10[n – Q] и A11[n] = A00[n – Q], а суммы (9) можно рассчитывать рекурсивно: Akm [П] = Akm [n -1] - am [n - M] + am [n], что позволяет существенно сокр атить количество операций при их вычислении. Комбинации (4) теперь будут описываться следующими выражениями:

n

B1[n] = Ao2[n]- A20[n] = 2MX1 X2 sin(®QA)cos(®QA)sin(y) + £ (a02[l]-a20[l]), l=n - M+1

B 2 [ n ] = A o 1 [ n ] - A io [ n ] + A 1 [ n - Q ] - A io [ n - Q ] =

n

= 2 MX i X ₂ sin( ® Q A )sin( y ) + £ ( a oi [ l ] -a_w [ l ] + a oi [ l - Q ] -a_w [ l - Q ] ) , l = n - M + 1

n

B3 [n] = 2Aoo [n - Q] - Ao2[n] - AM [n] = 2MXiX2 sin2(®QA) cos(y) + £ (2aoo [l - Q] - ao2 [l] - a2o [l]), l=n - M +1

а оценки частоты и разности фаз примут вид:

1          _ I B 1 [ n ] 1

® [ n ] = arccos          ®® + o_m [ n ],

Q A       V B 2 [ n ] J

V [ n ] = arctg

I

B 2 [ n ]

В з [ n ]

v

1 1 [ B 1 [ n ] ] \ V B 2 [ n ] J

V + \ [ n ].

Здесь введены следующие обозначения для дискретизированных функций ошибок:

n

£ (( a o1 [ l ] -a_w [ l ] + a 12 [ l ] -a 21 [ l ])cos( ® Q A ) -a o2 [ l ] + a 2o [ l ])

5 _m [ n ] = ^ ^ n - M ^--------------------------------------------------------------

2 X 1 X 2 Q A sin 2 ( ® Q A ) sm( v )

n

£ (2 a_n [ l ] -a o2 [ l ] -a 2o [ l ])sin( v )            . .

• 5, [ n ] = - ™                    +--- Cos^--- x

• ^v               2 X 1 X 2 sin> Q A )          2 X 1 X ₂ sin³( ® Q A )

На рис. 1 приведена структурная схема аппаратной реализации предложенного метода. Для расчёта очередной оценки частоты и угла фазового сдвига по рекурсивной схеме требуется 9 умножений 16 сложе- ний и вычисления трех функций: arccos(x), arctg(x / y) и квадратного корня. Также требуется пять массивов памяти по M ячеек, два массива – по 2Q ячеек и ещё два объёмом Q ячеек.

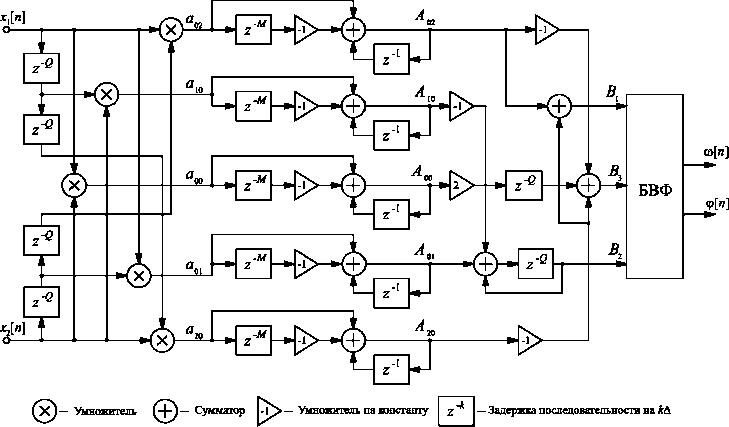
Pис. 1. Структурная схема аппаратной реализации рекурсивного оценивания частоты и угла фазового сдвига. На схеме прямоугольник БВФ обозначает блок вычисления функций

Таким образом, с помощью предложенного метода можно наблюдать динамику изменения во времени оценок частоты (10) и угла фазового сдвига (11), обновляя их значения с получением каждой очередной пары отсчетов сигналов x 1 [ n ] и x 2 [ n ]. Полученные значения оценок соответствуют середине скользящего окна [( n – L +1), n ]. Неограниченный рост ошибки определения частоты при у^- 0 можно скомпенсировать. Если оценка разности фаз мала, для определения частоты следует использовать отсчеты одного из исходных сигналов (например – x 1 [ n ]) и отсчеты вспомогательного сигнала x 3 [ n ] = x 2 [ n – S ], то есть искусственно ввести дополнительную разность фаз: ш S А .

При расчёте оценок частоты (5) и угла фазового сдвига (6) можно также применять метод наименьших квадратов. Введём новые обозначения:

n

Cij[n]= L bi[l]bj[l], l=n - M +1

где b i,j [ l ] – дискретные образы выражений (4); например, сочетание C 12 [ n ]равно

C 12 [ n]= L ( a 002 V ] - a 20 [ l ])( O »[ l ] - M l ] + a 12 [ l ] — a 21 [l D- l=n - M + 1

Используя новые сочетания, с помощью метода наименьших квадратов построим следующие оценки мгновенной частоты и угла сдвига фазы:

^v

ю [ n ]

= arccos

Q А

^*

v [ n ]

( C 12 [ n ] 1

I C 22 [ n ] J ’

C 23 [ n ]  1

C 33 [ n ] V

( C 12 [ n ] 1

I C 22 [ n ] ^J

Численное моделирование показало, что дисперсия этих оценок совпадает с дисперсией оценок, полученных по формулам (10) и (11), а смещение примерно в 100 раз больше. Кроме того, для оценок (12) потребуется в M раз больше сложений и умножений.

Результаты и обсуждение

Для проверки полученных соотношений был проведен ряд численных экспериментов. На рис. 2 и рис. 3 показаны зависимости среднеквадратичных отклонений ошибок определения частоты и разности фаз в зависимости от юА при у = 0,85 и в зависимости от у при юА =1,445. Обрабатывалось L = 2 Q + M ( Q + 1, M =55) отсчетов сигналов с постоянными амплитудами X 1 = 1,04 и X 2 = 1,32 и аддитивным нормальным шумом ( o i = 0,11 и а ₂ = 0,095), использовалось 100 реализаций. На рис. 3 сплошной линией показана граница Рао–Крамера, вычисленная для этих условий.

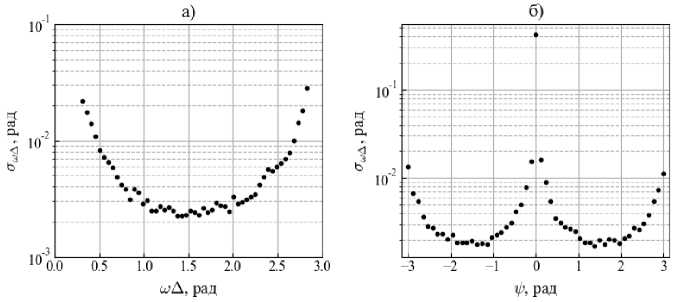
Pис. 2. Зависимость СКО ошибки оценки частоты от частоты сигналов (а) и разности фаз (б)

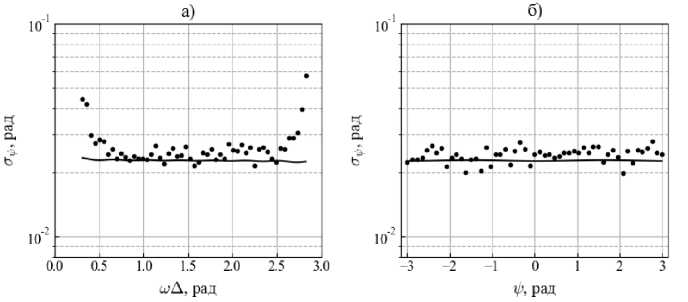
Pис. 3. Зависимость СКО ошибки оценки угла сдвига фазы от частоты сигналов (а) и разности фаз (б)

Численное моделирование показало, что оптимальное значение частоты сигналов находится в диапазоне п /5 <юА< 4п /5. При выполнении этого усло- вия оценка угла сдвига фазы обладает минимальной дисперсией, которая близка к границе Рао–Крамера. На практике удовлетворить этому условию можно соответствующим выбором частоты дискретизации и коэффициента прореживания Q.

Как уже отмечалось, достоинством предлагаемого метода является его устойчивость при одновременном наличии амплитудной и частотной модуляции. Следующий численный эксперимент заключался в обработке сигналов с тональной амплитудной и частотной модуляцией и аддитивным шумом (см. рис. 4), описываемые следующими моделями:

x 1 [ n ]= X 1

1 + Y1sinI —nЛ + ф1 I Isin(0[n]) + ^1[n], x2[ n ]= X2 1 + y2sin    n Л+ф2 sin(0[ n ] + у) + ^2[ n ],

I         IT2

где полная фаза и частота определяются выражениями

I        v,,T„

0 [ n ] = 0 0 + ® o n Л +  --- sin     n Л + ф_и

I     2nl

и [ n ] = и 1 + y_m cos     n Л + ф    , n = 0,..., N - 1.

I l T J)

В моделировании использовались следующие параметры: X 1 = 1,0, X 2 = 1,4, d = 0,04, 0 2 = 0,019, Y 1 = 0,1, Y 2 = 0,32, T 1 = 630 Л , T 2 =1780 Л , ф 1 = 0, ф 2 = 0, 0 0 = 0,11, Ю 0 = 0,132, у_и = 0,428, T и = 2100 Л , ф и = 0,11 и у = 0,815. При обработке применялось скользящее окно длительностью L =2 Q + M = 106 ( Q = 13, M=80).

На рис. 5 показаны исходные и восстановленные законы изменения частоты и разности фаз. В диапазоне от ( L –1)/2 до N –( L –1)/2 ошибки определения частоты и разности фаз не превышают 0,0088 и 0,023 соответственно.

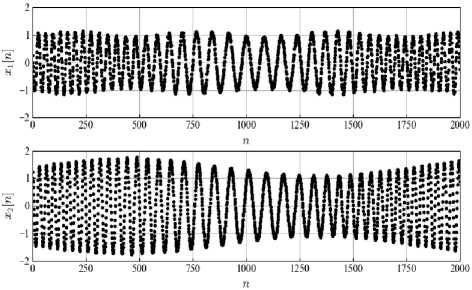
Pис. 4. Модельные сигналы x 1 [n] и x 2 [n] с медленно меняющимися амплитудами и частотой

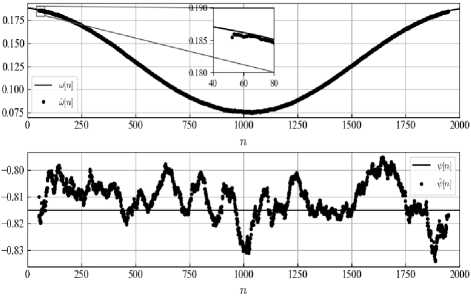
Pис. 5. Исходные и восстановленные законы изменения частоты и разности фаз

Заключение

Предлагаемый метод является «методом реального времени», поскольку ему требуется малое количество вычислительных операций по сравнению с другими методами, и он позволяет получать очередные оценки частоты и угла фазового сдвига за интервал дискретизации Л . В работе [11] приводится сравнение производительности методов оценивания полной фазы сигналов. Так, например, алгоритм, использующий дискретное преобразование Гильберта, потребует чуть больше 2 M операций сложения и столько же умножений, где M – длина окна усреднения.

Описанный метод может быть реализован на базе недорогого современного микроконтроллера или ПЛИС при частотах дискретизации до нескольких мегагерц. Например, популярный контроллер серии STM32F4xx имеет встроенный математический сопроцессор и позволяет выполнять умножения и сложения чисел с плавающей запятой одинарной точности за 1 такт; деление и извлечение квадратного корня за 14 тактов. Согласно официальной документации [12], на вычисление функции arccos с помощью алгоритма CORDIC потребуется около 350 тактов. Табличный метод позволит увеличить скорость вычисления функции, но для реализации потребуются допол- нительные затраты памяти программ для хранения таблиц значений. Большим достоинством предлагаемого метода является независимость количества операций от длины скользящего окна L. Это позволяет в процессе измерения регулировать параметр L (как коэффициент прореживания Q, так и количество усреднений M) в случае, когда значительно меняется скорость изменения измеряемых величин, то есть ввести в процесс элемент адаптации.