Метод оценки частоты генераторов в условиях непрогнозируемого изменения длительности интервала измерений

, например, в радиолокационных или радионавигационных системах, можно ограничиться только знанием частоты генераторов, чтобы учесть это значение при определении навигационных параметров 5].

В настоящее время для определения и стабилизации частоты генератора наиболее широко используется способ с применением фазовой автоматической подстройки частоты (ФАПЧ) [6-11]. Реализующее данный способ устройство включает эталонный и подстраиваемый генераторы, фазовый детектор и управляемый элемент. Однако высокостабильный генератор является сложным и дорогим техническим устройством. Это связано с построением высокодобротных контуров и формированием высокостабильных колебаний [12, 13]. В то же время в современных инфокоммуникационных систе-

16]. При отсутствии высокостабильного генератора частоты каждого из совместно и независимо функционирующих генераторов могут оцениваться так, как предложено в [17, 18]. Однако данный способ не позволяет учитывать изменения параметров генераторов при изменении внешних условий, что приводит к снижению точности оценок частот генераторов.

Целью статьи является разработка метода, обеспечивающего повышение точности оценивания частоты генераторов в процессе жизненного цикла радиоэлектронной системы с учетом нестабильности температуры, напряжений и т. д. При этом предполагается, что отсутствует высокостабильный дополнительный генератор и с этим связано непрогнозируемое отклонение длительности временного интервала.

Теоретические основы метода оценивания частот генераторов в условиях непрогнозируе- ных в составе радиоэлектронной системы или комплекса. Номинальные значения частоты генераторов и их относительные нестабильности известны и равны соответственно f0 и ok (k = 1,...,К + 1-\ Для каждого из данной совокупности K генераторов в течение интервала длительностью Ти производится измерение полной фазы f, колебаний его выходного сигнала ( к = 1,...,К). Это происходит при текущих условиях эксплуатации, одновременно, в течение одного и того же временного интервала измерений, задаваемого (К + 1) -м генератором.

В результате воздействия внешних факторов (например, нестабильности температуры, напряжения), частоты всех генераторов отличаются от номинальных значений — на величину I\f_k (к = 1,...,К + 1), а длительность временного интервала — на величину 6Т_И = -Т_й х М_к+1^_ок+1 .

Чтобы оценить отклонение частоты каждого из совокупности К генераторов, измерим полную фазу его колебаний ф, и определим отклонение Дф, полной фазы колебаний относительно ее номинального значения ф _Ок :

Аф, = ф,-фо,, 1 = !,..., К .                                    (1)

Значение фо, соответствует полной фазе колебаний сигнала номинальной частоты f_Qk за временной интервал измерений номинальной длительности Т_и .

Отклонение Аф, после линеаризации (отбрасывания слагаемого ^fk -ЪТИ) определяется дву мя слагаемыми:

• —    составляющей отклонения, определяемой отклонением частоты самого к -го генератора и равной Аф; = Ы\-Т_И;

• —    составляющей отклонения, определяемой отклонением длительности временного интервала измерений от номинального значения и равной Дф" = f0 5 Т_и .

При использовании метода ФАПЧ (А' + Ц -й генератор, применяемый для задания временного интервала измерений, является высокостабильным (его стабильность гораздо выше по сравнению с остальными К -генераторами). Поэтому ДА,- ДА (к = 1,..., К), и для всех ^-генераторов можно считать Дф" « Дф). С учетом последнего получаем, что Дф) = Дф,, и определяем отклонение частоты к -го генератора (к = 1,...,К ) по результатам измеренного отклонения фазы колебаний от номинального значения с использованием соотношения ДА, = ^_к/Т_и . Однако в рассматриваемом случае отсутствует высокостабильный генератор, обе составляющие отклонения фазы являются соизмеримыми и по результатам одиночных измерений не могут быть разделены. Таким образом, возникает задача оценки частоты генераторов в условиях непрогнозируемого изменения интервала измерений.

Для разделения составляющих Дф) и Дф) необходимо получить оценку 6Т_И и затем определить частоту колебаний каждого генератора при данных условиях эксплуатации. Для этого используется соотношение:

f_k =       ^5 L , _{k = r}._iK                                 (₂)

' и

Для определения ЪТ_И составим функцию правдоподобия [19]

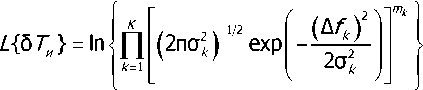
Коэффициенты тк (к = Х,,.,К) определяют степень влияния отклонения фазы каждого гене ратора на точность оценивания отклонения длительности интервала измерений от номинального зна- чения. При записи соотношения (3) было учтено, что отклонения частот генераторов от номинальных значений ^fk (к = 1,...,К) определяются влиянием большого числа независимых и равнозначных факторов и, соответственно, подчиняются нормальному закону распределения. С учетом выражения (2) функция правдоподобия (3) приводится к виду

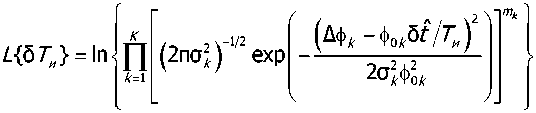
В качестве искомой оценки 6Т_И выберем значение, при котором функция (4) достигает максимума. Соответствующее значение равно

1(/77,Дф,о к2/0 , 1)

.

6Г = г А 1

к= 1

Доказательство, что найденная в (5) оценка отклонения длительности временного интервала измерений обеспечивает максимум функции правдоподобия, легко получается из исследования второй производной функции (4).

Значение 6Т_И после подстановки в (2) позволяет получить оценку частоты к -( к = 1,..., К) с использованием выражения

к

0 к

.

Данное соотношение полностью решает поставленную задачу получения оценки частоты каждого из совокупности одновременно и независимо функционирующих генераторов в условиях непрогнозируемого изменения интервала измерений.

Введение коэффициентов т_к позволяет увеличить число степеней свободы в управлении величиной получаемой оценки и компенсации воздействия различных факторов. В частности, как отмечалось выше, в течение жизненного цикла происходит изменение параметров отдельных генераторов, изменяется их нестабильность о² . Для компенсации указанных эффектов необходимо изменять параметры вычислительного алгоритма, на основе которых получается оценка 6Т_И в (5). При этом достаточно обеспечить выполнение условия т_к -о^² = const . Это технически значительно проще, чем использование, например, систем термостабилизации, чтобы в течение всего цикла работы системы обеспечить стабильность частот генераторов.

Свойства получаемых оценок. Исследуем свойства получаемых оценок. Для определения математического ожидания получаемой оценки f_k используем выражение

.

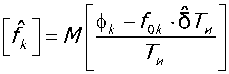
С учетом свойств математического ожидания преобразуем выражение (7) к виду

.

Для дальнейших преобразований используем выражения (2) и (5). В частности, для М[ф^]

можно записать

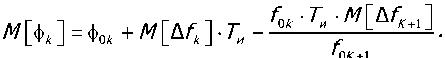
Из выражения (9) с учетом сделанных предположений о характере статистического распределения отклонении частот генераторов непосредственно следует, что /^^ф^^ — ф0k. Аналогично можно показать, что

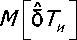
= 0. Таким образом, из (8) следует, что математическое ожидание оценки ча стоты к-                       0к,к = 1,...,К, т. е. получаемая оценка частоты генератора является несмещенной [20].

Вычислим дисперсию получаемой оценки. Воспользуемся выражением (6), в котором случайной величиной является только оценка отклонения длительности временного интервала от номинального значения. В этом случае, основываясь на результатах [19], получим

^[^^^ 2        , к = 1,..., К .                              (10)

Чтобы найти Z?^57^|, основываясь на (5) и учитывая, что первый начальный момент случайной величины 6Т_И равен нулю, запишем выражение для второго центрального момента (дисперсии) :

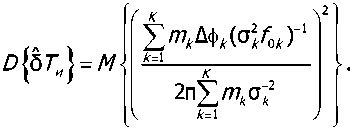
Выполняя последовательно преобразования в (10), получим

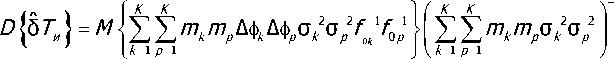
Учитывая, что отклонения частот генераторов являются некоррелированными, получаем

.

0,             .

Тогда представление для дисперсии 6Т_И имеет вид

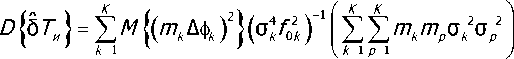
Принимая во внимание представление Дф^ = Дф^ +Дф" из (1), получаем

^{(Дф.)2} = ^ 02(/02 °2+ / 02 1о2 + 1).

Следовательно, окончательное выражение для дисперсии оценки временного интервала имеет вид

о[8г,}

t 0^{2      2} V 0² д ²    0² г₊ 1 О ² ₊ 1 )(° ⁴ / 0²

___ к= 1

I                   _-2 _-2 I

2 2 m_km o_k 22 к p к P \

1 p- 1

Таким образом, дисперсия оценки частоты генератора определяется формулой

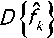
/ 0² t 0² Ъ^{т 2} (/ 0² О ² +/ 0² 1 О ² 1 )(° ⁴ / 0^{2 1}

___________1

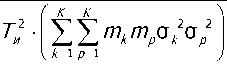
Рассмотрим частный случай, при котором все генераторы работают на различных частотах

/₀ k*t 0 ( к = 1,..., К* 1) и имеют одинаковые относительные нестабильности о_k- о( к = 1,..., К ) . Исследуем характеристики распределения отклонений частот генераторов от номинальных значений для данного случая. Исходя из того, что первый начальный момент случайной величины Аф^ равен нулю, на основании соотношения (16) запишем выражение для второго центрального момента (дисперсии):

К f02.t02 О2Тт2 (/02;+/02 1)

^И= к 1-        .                      (18)

L ²

к= 1 р- 1

В случае одинаковых значений весовых коэффициентов тк (к = 1,...,К) величина дисперсии определяется выражением

Как следует из (18)

^{4}

К f2t2п2V(f2 . + 2 'I 0kL00к ' 0K+1

k= 1

Т ² К ²

lim о^Д =0,

следовательно, данная оценка является асимптотически эффективной [20].

Для проверки свойства состоятельности получаемой оценки воспользуемся неравенством Чебышева. В соответствии с последним условием, для любого положительного числа s вероятность отклонения оценки частоты генератора fk отего математического ожидания не меньше чем на е огра ничена сверху величиной D^f^s .

В рассматриваемом случае получаем

С учетом формулы (18) последнее выражение преобразуется следующим образом: 222    2   2

/I А I \   0 k^L 00 к “^г * 0 К+ 1

—^к-1₂ К 2  ^{0 1} ,                          (22)

и откуда следует, что оценка является состоятельной [20].

Выводы.

• 1.    Предложенный метод статистической обработки результатов измерений фаз колебаний одновременно и независимо функционирующих генераторов в условиях непрогнозируемого изменения длительности интервала измерений позволяет получать оценки частот генераторов. При этом на параметры генераторов (частоту и стабильность частоты колебаний) не накладываются никакие ограничения. Метод позволяет значительно упростить построение систем, обеспечивающих стабильность параметров генераторов, путем применения весовых коэффициентов, используемых при получении оценок частот генераторов.

• 2.    Как показали результаты исследований, получаемые с использованием данного метода оценки частот генераторов являются несмещенными, состоятельными и эффективными.