Метод оценки числа объектов инфраструктуры в заданном диапазоне электропотребления при недостатке статистической информации

Для создания программ развития, планирования деятельности в сфере повышения энергоэффективности и энергоаудита необходимо знать, как распределены объекты в том или ином диапазоне электропотребления в исследуемом промышленном регионе. Информация подобного рода сопряжена с получением и обработкой данных из множества различных, в том числе противоречивых и взаимно дублирующих источников. В связи с этим возникает вопрос: существуют ли другие способы получения достоверной информации о распределении объектов по электропотреблению? С точки зрения теории информации можно снизить объем обрабатываемых данных, если есть определенные априорные сведения о структуре исследуемого объекта. Такими априорными данными может быть описание инфраструктуры объектов электропотребления как техноценозов.

Многочисленные исследования структуры потребителей электроэнергии, входящих в областные или краевые административные подразделения, показывают, что совокупность всех малых, больших предприятий, компаний и различных муниципальных учреждений, находящихся на данной территории, представляют собой техноценоз [1-3].

Совокупность объектов, представляющая техноценоз, характеризуется формой рангового распределения основного признака и формой рангового распределения видовой численности [4]. Первое распределение получается путем упорядочивания объектов в порядке убывания значения основного признака, второе – путем разбиения всей совокупности на подмножества и упорядочивания их по убыванию количества объектов в них. Оба эти распределения связаны друг с другом и должны иметь гиперболический характер.

В качестве основного признака будем рассматривать годовое электропотребление W (кВт∙ч). Ранговое распределение

W = W ( r )                                                            (1)

в случае техноценоза будет иметь вид как на рис. 1.

Из рангового распределения (1) можно составить видовое распределение ю = ю (n),                                                                       (2)

где ω – количество элементов вида n ; n – номер вида. Зависимость (2) можно получить путем разбиения множества рангов, которое есть подмножество натуральных чисел от 1 до некоторого r _max (для рис. 1 r _max = 79), на подмножества с количеством, соответствующим гиперболической зависимости элементов, в которых электропотребление элементов мало отличается друг от друга. Искомое разбиение определяется упорядоченным множеством рангов:

r l = 1 <  r <  ... <  r m = r max .                                                           (3)

В’

12 1-

ОД .

ОД.

ол

1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77

Рис. 1. Ранговое распределение

JF

од

0.6

0.4

О

I

I

■

•                 ■                   •                     >

IJIIIIM^^

JIS К 13: 17 f1 25 ;29 33 ;37 41 45 49 53; 57 61 6? 69 73 77

Г, Г. Г_А                     •••                                            'll            Ц;

Рис. 2. Выделение видов

На рис. 2 изображено, как множество рангов (3) выглядит на графике рангового распределения. Если в последовательность (3) добавить r ₀ = 0, то количество элементов вида n будет определяться как разность соседних рангов, определяющих заданный вид:

“ ( n ) = r m - n + 1 - r m - n .

Пусть зависимость (2) имеет вид

a

® ( ⁿ ) = ""c , ⁿ

где a и С – константы. Тогда процесс получения зависимости видового распределения (2) можно осуществить следующим образом. Предположим, что выделено m видов, тогда вид с номером m имеет один элемент - щ( m ) = 1. Подставив это значение в (5), получим выражение, связывающее константы a и С :

a = m^C .

Из (4) для n = m - 1 получаем

ю ( m - 1) = r₂ - 1

и, подставляя в (5), получаем r2

a

( m - 1) C

+ 1.

Для произвольного n получается формула

a

(9а)

r , = —- + r m - n+1      C m - n

n или с учетом (6)

Г m - n + 1

C m ] n J

.

r m - n

(9б)

Используя вышеописанный алгоритм для рангового распределения, изображенного на рис. 1, получаем видовое распределение на рис. 3.

Рассмотрим обратный процесс – получение рангового распределения из видового. Конечно, имея только одну зависимость (5), невозможно восстановить даже приблизительно зависимость (1) – недостаточно информации. Поэтому как минимум необходимо знать среднее электропотребление по номеру вида W ( n ) . Будем предполагать, что ранговое распределение имеет вид

W ( r )= r C ^.

Из (10) получаем

Г ь ) C 1 r =          ,

IW J

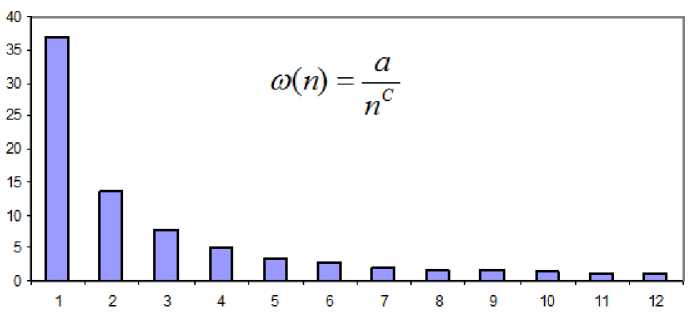
Рис. 3. Видовое распределение

где b и C ₁ – константы. Тогда из (4), (5) и (11) будем иметь такое выражение:

a _f b ^C 1   f b ^C 1

n C I W ( Г т — n + 1 ) J    I W ( Г т — n ) J

Для n = m выражение (12) будет иметь вид

1 — f b ) C1 — l W (1) J

Поскольку вид с номером m имеет только один элемент, то

W (1) — W ( m ) — b .

Для n = m – 1 выражение (12) будет иметь вид

C 1

a

( m — 1) C

b

_ W ^{(1 +} mh C ) ,

1 f b ) C к W (1) J

Из (15) определяем очередное значение W ( г ) для г — 1 +

a

( m — 1) C :

W (1 + — a -^) — ( m — 1) C

_f                               1

a • ( W (1 ) C ¹ + b C ¹

• ( m — 1) C

C 1

.

к      ( m — 1) C • ( W (1) C 1       j

Для произвольного n очередное значение W ( r ) будем находить по формуле

n

W ( Z a^) )

k — 1 ^k

n+1 /7   —    — a • (W(Z^C) C1 + bC1 • nC k—1 k

C 1

к

n+1 a X nC • (W(Zo^)) C- k—1 k            J

.

Получающиеся значения для W ( r ) в (17) должны удовлетворять условию

W ( n ) <  W (J- O r) <  W ( n — 1). k — 1 k C

Если условие (18) не выполняется, то либо элементы не оптимально распределены по видам, либо рассматриваемая совокупность не техноценоз.

Итак, если некоторая совокупность электропотребителей является техноценозом, то их ранговое распределение по электропотреблению будет описываться зависимостью вида (10). Соответственно, обратная зависимость будет иметь такой же вид, только с другими параметрами:

a

r W C .

Величина r2

aa

r = r1   W1C   W2C ,

определяющая количество электропотребителей, находящихся в диапазоне электропотребления от W 1 до W 2 , говорит о том, что выражение (19) есть интегральная функция распределения электропотребителей. Соответственно, производная выражения (19) будет определять функцию плотности распределения по электропотреблению:

d ( - a A dW ( WC J

c • a

W C + 1 ,

где ρ ((кВт∙ч)-1) – количество потребителей на кВт∙ч.

Выражение (21) имеет такой же вид, как (19), поэтому, изменив в нем константы, перепишем в виде

a

p =--F.

W ^C

В любом случае выражение (22) является приближением реальной функции плотности. Поэтому, чтобы повысить точность модели, рассмотрим более сложный вариант гиперболической зависимости – с тремя параметрами:

a ■ W + b

W ^C

Оценим параметры функции плотности электропотребителей (23) на примере Красноярского края. Для этого составим систему из трех уравнений. Первые два уравнения будут описывать две крайних точки распределения (23). Третье – определять полное электропотребление в крае, которое устанавливаем из (23):

W max

W^ = J p WdW =( min

a

b

(3 - C )W C ^{- 3 +} (2 - C )W C - 2

)

w„ max

.

min

Система уравнений относительно неизвестных a , b , c будет иметь вид

a^W min ^{+ b} = p

C            min min

aWmax + b = w C p max

aba

------------TT^r +--^---TT^T

C-3  (2-cW c  (3-cWC-3

(3 c ) W _max   (2   c ) W _max   (3   c ) W _min

b

(2 - c )W 2—^ c

= W .

Определим значения констант в системе уравнений (25) на примере Красноярского края. На основе специального исследования электропотребление средней городской квартиры, W min – ми- – 1015 –

нимального элемента в техноценозе, берется равным 3000 кВт∙ч. Плотность числа минимальных электропотребителей, ρ min , определяется как отношение приближенного числа квартир в крае к вариации их электропотребления, 560000/4500 = 124,44. Электропотребление самого крупного элемента техноценоза, W max – ОАО «РУСАЛ Красноярский алюминиевый завод», – 14,3∙10⁹ кВт∙ч. Плотность числа максимальных электропотребителей, ρ _max, определяется величиной, обратной разнице электропотребления максимального элемента техноценоза и следующего за ним (ОАО «ГМК Норильский никель» с потреблением 6,4∙10⁹ кВт∙ч), 1/(14,3∙10⁹ -6,4∙10⁹ )=1,27∙10^-10. Суммарное энергопотребление Красноярского края, W Σ , 5∙10¹⁰ кВт∙ч.

Система уравнений (25) не имеет аналитического решения. Значения неизвестных были получены с помощью пакета MatLab:

a = -0,0223, b = 3,69 -108, c = 1,86. (26)

Исходя из полученных параметров распределения (23) можно в качестве примера найти количество предприятий, попадающих в диапазон электропотребления от W 1 = 10⁷ до W 2 = 10⁹ кВт∙ч.

N = ^a (3 - c ) W ₂ ^{C - 3}

ba

+-

(2- c ) W ₂ ^{2 - c}   (3- c ) W ₁ ^{C - 3}

b

(2 - c ) W ₁ ^{2 - c}

≈ 391.

Таким образом, адекватность описания инфраструктуры электропотребителей как техноценоза дает необходимую информацию для построения функции распределения (23). Это позволяет найти количество объектов в заданном диапазоне электропотребления и суммарное электропотребление этих объектов.