Метод оценки энергетической эффективности ДОЭ

Дифракционные оптические элементы (ДОЭ), предназначенные для фокусировки лазерного излучения и известные как фокусаторы [1-3], позволяют сформировать в фокальной области требуемое распределение интенсивности. При этом качество фокусировки зависит от методов изготовления дифракционного микрорельефа ДОЭ. Для оценки качества фокусировки на этапе проектирования фокусаторов используется математическая модель, представляющая ДОЭ как набор модулей кольцевой, линейной или прямоугольной формы [4-6].

Такая модель предполагает кусочнопостоянную аппроксимацию микрорельефа ДОЭ, что характерно, например, для литографических технологий [7-9].

Однако существуют и развиваются альтернативные технологии изготовления ДОЭ, обеспечивающие более сложную (например, кусочнолинейную) аппроксимацию профиля дифракционного микрорельефа ДОЭ [10-15].

В настоящей работе предложен метод оценки энергетической эффективности ДОЭ на стадии проектирования. Метод может быть использован для оценки влияния различных технологических ошибок изготовления на работу дифракционных оптических элементов.

1.    Постановка задачи

Пусть ϕ(u,v) есть фазовая функция ДОЭ, фоку- сирующего лазерный пучок света с комплексной амплитудой W(u,v) в область Q фокальной плоскости (Рис.1). Важнейшим критерием оценки работы ДОЭ является энергетическая эффективность [4-6, 16]

∫∫ I ( x , y ) dx d y

E= ^Q                                  (1)

∫∫FW(u,v) I 2 dudy где I(x,y) - распределение интенсивности в фокальной плоскости, а F - апертура ДОЭ. Значение E характеризует долю энергии освещающего пучка, фокусируемую в требуемую фокальную область Q.

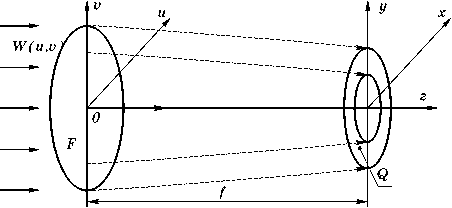
Рис. 1. Геометрия фокусировки

Предположим, что технологические погрешности изготовления ДОЭ могут быть описаны в виде нелинейного преобразования G[ϕ] фазовой функции ДОЭ ϕ(u,v). Например, погрешность фотолитогра- фической технологии описывается квантованием фазовой функции y(u,v), приведенной к интервалу [0, 2п). В этом случае функция нелинейного предыскажения фазы G[ф] будет иметь вид

G Ы= int 7- А, L A J

А = 2 п / M

где int[x] - целая часть от x , а M - число уровней квантования фазы.

Целью настоящей статьи является получение оценок изменения энергетической эффективности ДОЭ для некоторых функций искажений G[ ф ], описывающих технологические погрешности изготовления дифракционного микрорельефа.

• 2.    Оценка энергетической эффективности ДОЭ

С учетом технологических ошибок изготовления функция комплексного пропускания ДОЭ имеет вид

T(u,v) = exp(i G [ ф (u,v) ])                       (2)

Чтобы описать работу оптического элемента (2), разложим функцию T(u,v) в ряд Фурье [17-18]

по переменной ф n =- « где N - количество зон микрорельефа ДОЭ, cn =

2 п N

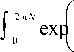
iG [ Е ] - iN е] d Е

n =+ «

I C n l² = 1

В соответствии с (3) комплексная амплитуда поля в фокальной плоскости элемента (2) описывается выражением n=+ «

^{W (} x , У ) = I cW. ⁽ x , У )

n =- «

В приближении Френеля-Кирхгофа W_n(x,y) имеет вид

W ( x ) =     Я E o ( u )

i f F

x exp i — ф ( u ) - i— ( x - u )² d ² u \ N ’   2 f^v     ’ J

[19-20]

где x =(x,y), u =(u,v) , к=2п/Х, X - длина волны, а f -расстояние до фокальной плоскости.

В соответствии с (5) и (6) элемент (2) формирует дифракционные порядки Wn(x,y), П = —^, го . Требуемая фокусировка описывается членом WN(x,y). Численный анализ интеграла (6) для n ^N показывает его малость по сравнению с интегралом WN(x,y) для случая фокусировки в линию. В частности, как следует из общего представления фазовой функции фокусатора в линию [2, 6, 21] члены Wn(x,y), n ^N, соответствуют расфокусированным линиям. Дифракционная ширина таких линий на порядок больше дифракционной ширины линии, описываемой членом ряда WN(x,y). Поэтому при фокусировке в линию с хорошей точностью можно использовать следующее соотношение

^{W (} x , У ) = c N ^W N ^{( x} , У ) ⁽⁷⁾

Согласно (1) и (7) получаем оценку энергетической эффективности ДОЭ (2) в форме

E = C n I² E (8)

где E - дифракционная эффективность ДОЭ с фазовой функцией V (u,v) . Следует заметить, что (8) является оценкой снизу энергетической эффективности оптического элемента (2), так как паразитные порядки, соответствующие n ^ N , в некоторых случаях могут накладываться на полезное изображение, увеличивая энергетическую эффективность.

Как следует из (8), изменение энергетической эффективности ДОЭ, обусловленное нелинейным искажением G [ ф ] его фазовой функции, пропорционально квадрату модуля коэффициента Фурье c N в разложении фазовой функции exp(i G [ ф ]). Конкретная форма функции G [ ф ] зависит от типа технологических погрешностей и конкретной технологии изготовления ДОЭ.

• 3.    Расчет функции нелинейного искажения

В качестве примера рассмотрим расчет G [ ф ] для ДОЭ с аксиальной симметрией, изготавливаемых на прецизионных станках [10-12,15]. Особенностью такого метода изготовления является кусочно-линейная аппроксимация зон дифракционного микрорельефа ДОЭ, генерируемого радиальной фазовой функцией ф ( r ) е [0, 2 п N ], r = ( и² + v² ) ^1/2 , r е [0, R ]. Разобьем интервал [0, R ] на набор непере-секающихся отрезков [ U m , U m+1 ], каждый из которых подчиняется следующему условию

ф ( U m + 1 ) -ф ( U m ) = 2 п l , l = const , l ^ N (9)

Величину l можно интерпретировать как интервал приведения фазы (см.Рис.2). Предположим, что на каждом интервале [ U m , U m+1 ] функция G [ ф ( r )] является линейной и принимает на концах интервала значения 0 и 2 п l соответственно (Рис.2). В этом случае функция нелинейного преобразования (искажения) имеет вид

Е- f ( Е )

G [ Е ] = —74^1^2п l , Ее [ 0,2 п N ]    (10)

f2 (Е)-fl (Е)                                 ’ где fl «) = ф-'I 2nl int

^ 2 nl

f , ( ^ ) = ф 4 2 nl I int

_4_

2 nl

а ф -1 - функция, обратная к ф ( r ).

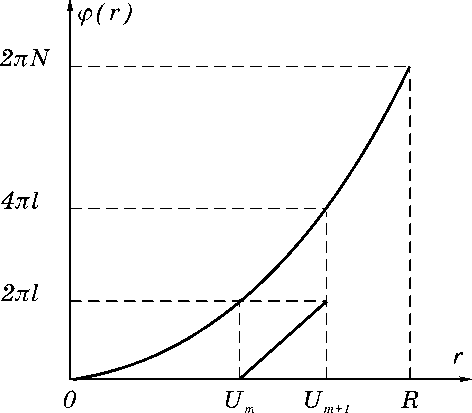
Рис. 2. Кусочно-линейная аппроксимация фазовой функции ДОЭ.

Чтобы оценить изменение энергетической эффективности на основе функции G [ ξ ], определенной в (10), были рассчитаны коэффициенты c_N ² для дифракционной линзы, задаваемой формулой

ϕ(r)= π (R2-r2);R=(2λfN)1/2 λf со следующими параметрами: λ=0.001 мм; f=100мм; N=4-100.

Графики фазовой функции линзы до и после нелинейного преобразования G [ ϕ ] показаны на Рис. 3(а,б).

В Таблице 1 приведены рассчитанные значения квадратов модулей коэффициентов Фурье c N для различных значений параметров N и l .

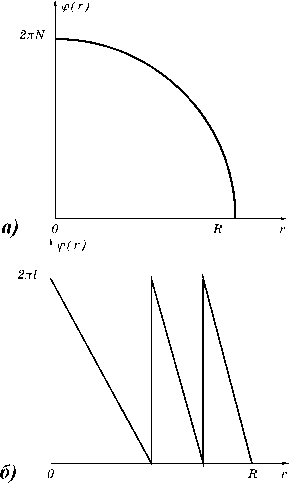
Рис. 3. Графики фазовой функции линзы до (а) и после (б) применения нелинейного преобразования G [ Ф ].

Данные, приведенные в Таблице 1, могут быть использованы для выбора допустимых параметров N и l дифракционной линзы при кусочно-линейной аппроксимации профиля зон микрорельефа. В частности, применение кусочно-линейной аппроксимации микрорельефа дифракционной линзы с вышеприведенными параметрами для количества зон N>4 и l=1 приводит к уменьшению энергетической эффективности не более чем на 20%. В то же время линейная аппроксимация сразу относительно боль- шого числа зон Френеля N/l<20 при l≥2 является неэффективной.

Таблица 1.

Значения |с„ |2, описывающие изменения энергетической эффективности для кусочно-линейной аппроксимации профиля микрорельефа дифракционной линзы

	N
l	4	8	16	20	40	50	100
1	0.8073	0.8837	0.9354	0.9471	0.9724	0.9772	0.9881
2	0.2573	0.4851	0.6967	0.7486	0.8646	0.8900	0.9440
5	-	0.3217	0.5562	0.6220	0.7635	0.7987	0.8831
10	-	-	0.1841	0.2225	0.3669	0.4198	0.5910
20	-	-	-	0.0221	0.0377	0.0690	0.1148

Работа выполнена в рамках Государственной научно-технической программы "Наукоемкие технологии" при поддержке Министерства науки и технической политики РФ. Авторы выражают благодарность А.Е.Царегородцеву, Я.Е.Тахтарову и С.В.Смагину за помощь в подготовке статьи.