Метод оценки надежности сложных систем, расчет которых не сводится к схеме последовательно-параллельного соединения элементов

В технике известны сложные системы, модель надежности которых не может быть построена непосредственным применением теоремы умножения вероятностей, как это делается для систем с последовательно-параллельным соединением элементов. При построении расчета для таких систем используется логико-вероятностное исчисление. Подробно методы логико-вероятностного исчисления рассмотрены в монографии [1], в которой использованы некоторые результаты.

В качестве примера из [1], рассмотрим мостиковую систему (рис. 1).

Рис. 1. Структурная схема мостиковой системы

Предполагается, что система откажет, если в ней выйдут из строя элементы 1 и 2, либо 3 и 4, либо 1, 5, 4, либо 2, 5, 3.

Решение задачи расчета надежности мостиковой системы в [1] получено с использованием логиковероятностного подхода, согласно которому исходная структурная схема (рис. 1) заменяется на эквивалентную (рис. 2).

Рис. 2. Логическая схема мостиковой системы, построенная по методу минимальных сечений

Для рассматриваемой системы расчет вероятности отказа Q при традиционном методологическом подходе может быть выполнен и с использованием теоремы умножения вероятностей. Тогда, при условии равенства вероятностей отказов q всех элементов, вероятность отказа системы запишется в виде

Q = 2 q ² + 2 q ³ + 2 q ⁵ - 5 q 4 .            (1)

Поскольку моделью (1) в [1] не накладываются ограничения на вид функции q для элементов, то в качестве последней примем распределение равномерной плотности вида

q ⁽ t) =

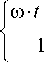
при 0 <  t <  T cp пРи t ^ T cp

где to = — - параметр потока отказов элементов, T cp

T _cp – средняя наработка на отказ элемента. Далее в расчетах примем параметр потока отказов одинаковым для всех элементов и равным to = 1 ■ 10 ^{- 4}.

Построим по (1) с учетом (2) зависимость изменения вероятности отказа системы от времени и проанализируем ее особенности (рис. 3, пунктирная линия).

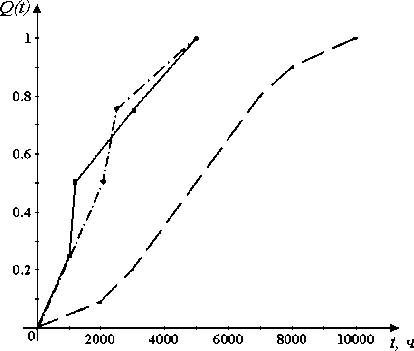
Рис. 3. Зависимость вероятности отказа мостиковой системы из 5 элементов при to = 1 ■ 10 - 4 :

- - - – традиционный метод расчета [1]; ––– – предлагаемый метод расчета с использованием логико-вероятностного представления; – · – – прямое применение предлагаемого метода

Прежде всего следует заметить, что графически форма зависимости (1) близка к интегральной функции нормального распределения, а следовательно, вероятность отказа системы за единицу времени будет иметь вид гауссовской кривой плотности вероятности. Если вероятность отказа за единицу времени будет описываться гауссовской кривой, то невозможно объяснить, почему она в начале будет возрастать, а затем, достигнув максимума, будет уменьшаться при неизменных структуре системы и вероятности отказа элементов за единицу времени. Второй вопрос состоит в том, что в этом случае вероятность отказа за единицу времени будет определяться неоднозначно. Если, для наглядности, приращение времени принять равным 2 000 ч, то следует, что на отрезках [0, 2000] ч и [8000, 10 000] ч (рис. 3, пунктирная линия) приращение вероятности отказа системы примерно одинаковы и составляют 0,18 (0,2). Но приращение вероятности отказа на отрезке [4000, 6000] ч в 3,5 раза больше.

Ответы на эти и другие вопросы, связанные с правомерностью применения теоремы умножения вероятностей в расчетах надежности, можно найти в работе [2].

Здесь остановимся на вопросах, не отмеченных в [2]. В частности, на вопросе о гладкости зависимости (1) (рис. 3, пунктирная линия). В постановочной части задачи расчета надежности мостиковой системы [1] отмечены сочетания числа элементов, при отказе которых система потеряет работоспособность. Однако отказы элементов – это дискретные события, происходящие в дискретные моменты времени. И в эти дискретные моменты изменяется структура системы, модель (1) никак не отражает. Кроме того, в соответствии с (1), вероятность отказа системы Q = 1 осуществляется только при достижении всеми элементами вероятности отказа q = 1. Такой вывод в корне противоречит исходным предположениям постановочной части задачи о том, что вся система откажет, если в ней выйдут из строя элементы 1 и 2 либо 3 и 4, либо 1, 5, 4, либо 2, 5, 3 [1].

В работе [3] предложен метод расчета надежности систем, исключающий применение теоремы умножения вероятностей. Метод основан на простом представлении о том, что плотность суммарного потока отказов совокупности n элементов, составляющих систему вне зависимости от схемы их соединения, значительно больше, чем у одного элемента.

Рассмотрим предлагаемый метод. Суммарный параметр потока отказов системы ок равен сумме параметров потоков отказов элементов составляющих совокупность:

№ = £ « , . (3) i = 1

Именно ок определит вероятность первого отказа элемента в рассматриваемой совокупности. При этом заранее неизвестно, какой именно элемент откажет первым, и какое место он занимает в схеме. При распределении равномерной плотности вероятности (2), принятом для вероятности отказов элементов, вероятность первого отказа q1 (t) в системе определится по выражению

n qi( t) = ti^®г i=1

Тогда, если задать вероятность q ₁ ( t ) = 1, то из (4) вычислим время работы системы до первого отказа:

t ₁

n

z«

i = 1

Поскольку элементы в системе соединены определенным образом, то в момент времени t1 , после отка- за первого элемента, структура системы изменится. В зависимости от схемы соединения элементов, их число в оставшейся работоспособной части системы изменится на некоторую величину k, где k – число элементов, исключаемых из системы вследствие первого отказа элемента. Тогда с учетом того, что элементы работоспособной части системы уже отработали время t1 , вероятность отказа второго элемента находят по формуле

П — k q 2( t) =(ti + A12) ■£«■.              (6)

i = 1

Далее, задавшись, как и ранее, q2 (t) = 1, найдем приращение времени до отказа второго элемента в оставшейся работоспособной части системы:

A 1 2 =

n — k

^{1 —} t 1 ■ ^ Ю /

___________ i = 1 n — k

Z®i i=1

тогда время до второго отказа t 2 = t1 + A t 2 .

Продолжая подобные операции, определим время t_j , j -го отказа элемента в системе, после которого она потеряет работоспособность.

В зависимости от принятой схемы соединения элементов, отказ каждого i -го (1 <  i <  j ) элемента приводит к изменению вероятности отказа системы на вполне определенную величину A Q i . Предлагаемый метод обеспечивает возможность поставить в соответствие каждому отказу элемента в определенный момент времени t_i конкретное значение вероятности отказа системы Q_i ( t ).

Для наглядности на рис. 3 приведены результаты расчета этой же мостиковой системы по предлагаемому методу без использования теоремы умножения вероятностей, но с применением расчетной схемы, приведенной на рис. 2, построенной по логиковероятностному методу (сплошная линия) и прямым применением предлагаемого метода к исходной расчетной схеме, приведенной на рис. 1 (штрих-пунктирная линия).

Точки излома на графиках (рис. 3, сплошная и штрих-пунктирная линии) соответствуют моментам времени отказов элементов, а число изломов – числу параллельно включенных ветвей логической схемы. Промежуточные отрезки между точками отказов элементов линейны, поскольку на этих промежутках структура системы остается неизменной.

Расхождение графиков (рис. 3, сплошная и штрих-пунктирная линии) не существенное.

В монографии [1] справедливо отмечается, что расчеты на надежность потенциально опасных сложных систем, отказы которых сопряжены с большими экономическими потерями, не могут быть сопоставлены со статистическими оценками, полученными как при испытаниях таких систем, так и в процессах их серийной эксплуатации. Испытания сложных систем чрезвычайно дороги, а по длительности сопоставимы со временем эксплуатации систем. По понятным причинам статистика катастроф самолетов и атомных электростанций крайне скудна для того, чтобы ее можно было использовать для получения статистических оценок надежности систем. Тем более, что катастрофы крайне редко связаны с отказами систем.

В связи с этим правомерность использования тех либо иных методов расчета надежности сложных систем может быть оценена только по корректности использования фундаментальных положений математики и по непротиворечивости результатов расчетов надежности исходным данным и феноменологическим представлениям о характере изменения вероятности их отказа.