Метод оценки надежности вычислительных систем

Основной характеристикой, формирующей техническую эффективность вычислительных систем реального времени, является надежность. Оценка надежности суперЭВМ, к которым относятся многопроцессорные вычислительные системы (МВС), работающие в реальном масштабе времени, часто производится посредством прогона типовых задач на изготовленных образцах. Однако на стадии проектирования данный способ вызывает большие трудности, связанные со значительными затратами времени и ресурсов на создание модели разрабатываемой МВС.

Известные методы оценки надежности МВС реального времени либо не учитывают характеристики алгоритмов, либо получены для оценки надежности МВС, состоящих из однородных процессоров, или МВС, состоящих из разнородных процессоров и имеющих одношинную организацию связи процессоров с общей оперативной памятью (ОП). В связи с этим возникает задача получения достаточно простых аналитических выражений для оценки надежности, учитывающих влияние как основных характеристик решаемых задач, так и основных параметров МВС.

Исследуемая многопроцессорная вычислительная система с осто ит из N типов процессоров, содержащих по m i ( i = 1 ,N ) процессоров каждого типа. Процессоры объединяются с ОП посредством п шин, причем в предельном случае количество шин может быть равно количеству процессоров (полносвязный интерфейс). Количество блоков общей оперативной памяти определяется необходимым объемом этой памяти.

Предполагается, что суммарный поток отказов от шин и процессоров всех типов подчиняется пуассоновскому закону распределения с параметром V . , а время восстановления шин и процессоров i -го типа - экспоненциальному закону с параметром m . .

Процесс надежности функционирования МВС представлен замкнутой системой массового обслуживания (СМО) с ожиданием.

Каждый процессор в некоторые случайные моменты времени выходит из строя и нуждается в восстановлении. Поток отказов от процессоров каждого типа и шин интереса - простейший с параметром V . , где i = 1, 2,..., N + 1 . Интенсивность восстановления каждого вышедшего из рабочего состояния элемента вычислительной системы подчиняется экспоненциальному закону распределения с параметром ц . . Если вновь поступивший на восстановление запрос застанет обслуживающий прибор свободным, то запрос принимается на обслуживание. Если же поступивший запрос застанет обслуживающий прибор занятым, то он становится в очередь и ждет своего обслуживания. Цисциплина обслуживания - случайный равновероятный выбор из очереди.

Рассматриваемая СМО может находиться в следующих состояниях:

• -    a ₀.₀.₀.....₀ - интерфейс и все процессоры неисправны и восстанавливаются. Вычислительный процесс остановлен;

• -    а ₁,₀,₀,...,₀ -исправна одна шина интерфейса, а ( т ₁ -1) шин неисправны и восстанавливаются; все процессоры неисправны и восстанавливаются. Вычислительный процесс остановлен;

• -    a ₀.₁.₀.....₀ - все шины интерфейса неисправны и восстанавливаются; все процессоры, за исключением одного первого типа, неисправны и восстанавливаются. Вычислительный процесс остановлен;

• -    a ₀.₀.₁.....₀ - все шины интерфейса неисправны и восстанавливаются; все процессоры, за исключением одного второго типа, неисправны и восстанавливаются. Вычислительный процесс остановлен;

• -    ^а ₀.₀.₀.....₁ - все шины интерфейса неисправны и восстанавливаются; все процессоры, за исключением одного N -го типа, неисправны и восстанавливаются. Вычислительный процесс остановлен;

• -    jj ₂ , j з >-> jN _{+ 1} - j i шин интерфейса исправны и участвуют в вычислительном процессе, а ( т ₁ -j ₁ ) шин неисправны и восстанавливаются;, / ₂ процессоров первого типа исправны и участвуют в вычислительном процессе, а ( т ₂ -j ₂ ) процессоров неисправны и восстанавливаются;, / ₃ процессоров второго типа исправны и участвуют в вычислительном процессе, а ( т₃-j ₃ ) процессоров неисправны и восстанавливаются; ...;j _{N н} процессоров N -го типа исправны и участвуют в вычислительном процессе, а ( m _N -j _{N +1} ) процессоров неисправны и восстанавливаются;

• -    a m , . m 2 . m . ..... m _{+ 1} - все процессоры и шины, входящие в состав вычислительной системы, исправны и участвуют в вычислительном процессе.

Используя правила составления системы дифференциальных уравнений, запишем систему дифференциальных уравнений рассматриваемой СМО:

dP     ( t )      N + ¹

---^"Г ----= - Е m ^ - P 0.0 0 ⁽ t ) ^{+ V} 1 P 0 0 ⁽ t ) ^{+ V} 2 ^P 0 , 1 0 ⁽ t ) ⁺ ••• dt             i = 1

^+V N + 1 ^P0,0..... 1⁽ t ).

dP        ( t )     N + ¹

^{i,i 2} ^j" ^{+ 1}   = - Е [( m i - i X + vJ P j 1 ,i ₂

dt              _{i = 1}

,^j N + 1

(t)+

^{+ (} m 1    ^j 1 ^{+ 1) Ц} 1 ^Pj 1 - 1,j ₂,j + 1 ⁽ t ) ^{+ (} m 2 ⁺ j 2 ^{+ 1) Ц} 2 P j . j ₂ - 1...... j N + 1 ⁽ t ) ⁺ ...

^{+ (} m N + 1    j N + 1 ^{+ 1) Ц} N + 1 P j . j 2 ..... j , + 1 - 1 ⁽ t ) ^{+ V} 1 P j + 1. j 2 ..... j , + 1 ⁽ t ) ⁺

+V₂ P -₊₁     ( t ) + ... + V_W PP, ,

² / 1 . ^j 2 ^{+ 1}..... ^jN + 1                          N ^{+ 1} / 1 . ^j 2 ..

^m 1 . m 2 ..... mN + 1

dt

( t )       ^N +1

=-Yxp ti i m 1 . m 2 i =1

+Ц9Р   ,

2 m_n m 2 -1..... m_N + 1

, ....

.. jN + 1 + 1⁽ t ).

..... mN + 1 ⁽ t ) ^+Ц 1 P m -1. m 2 ..... mN + 1 ⁽ t ) ⁺

⁽ t ) + ... + ^ц N +1 ^Pm„ m . ..... mN „

N +1

-

-1 ( t ).

Число состояний СМО равно й = П ⁽ mi ⁺ 1) .

i =1

Цля стационарного режима получим систему линейных уравнений:

N + 1

- X m i ^Ц i^P0_;0_;._;0 + ^V 1 P ,,..., + ^V 2 P 0,1,...,0 ⁺ ••• ^{+ V} N + 1 ^P 0,0,...1 = °* i = 1

N +1

- X [⁽ m i - ^ji ^{) Ц} i ^+V i ] P 1 , j2,-jN + 1 ⁺ i =1

⁺ ( m 1 - ^j 1 ^{+ 1) Ц} 1 ^Pj 1 - 1,j 2 ,...,jN + 1 ⁺

^{+ (} m 2 - ^j 2 ^{+ 1) Ц} 2 ^Pj_bj ₂ -1,..., J n + 1 ⁺ ... ^{+ (} m N +1 - ^jN +1 ⁺

+1)Ц P . + V. P         + ... +

^{N + 1} j 1 , j 2 ,... jN + 1 ^{1        1} j 1 ^{+ 1}> j 2 ,..., jN + 1

-VN^P ,      + +V.. , P

'- P 1 , j 2 +1,..., jN + 1 + ”. + ^V N + 1 P 1 , j 2

., ^jN + 1 ^{+ 1}

= 0.

N +1

У v p

— Z-^ I m1 , m 2

i =1

+ Ц            + ЦР ,+

,..., mN + 1        1 m -1, m 2 ,..., mN + 1         2   m_n m 2 -1,..., mN +

+Ц N+1 Pm1, m 2,..., mN+1 -1

Для решения системы уравнений (2) в общем виде подстановку [1]

N +1

j J2 „jN =П Л(3)

i =1

и перепишем систему линейных уравнений (2) в следую щем виде:

" ХК т , - У , ) ^ + V , ] ЄР, , • ...- Р„ „ + ( т , - j , + 1) rt^- p , ₌ - ...Р ,_ „ + ( т ₂ - j ₂ + 1)

• P  + (m2 - h + ЖP P , ... P +... + jN+1     v 2      2          2 j1 jV j2-1       jN+1

^{+ (} m N +1 - ^jN +1 ^{+ 1) -Ц} N +1 P P i ,- ^P J n + 1 -1 ^+V 1 P +1 ^Pj ₂-. ^P J n + 1 ⁺

+V₂ P P j... P + ... + V_W PIP P ... P j= 0. (4)

2 J1 h2+1       jn+1              N +1 J1 h2       Jn+1+1v 7

Перегруппируем (4) таким образом, чтобы P i входили в соответствующие выражения, содержащие m i , V i , Ц i , т е. произведем разделение переменных по индексам:

{(mi - ji + 1)V1 PJ1-1 - [(m1 - j1 )V1 + ^       ^     ^^

^{- j} 2 ^{+ 1) V} 2 P J 2-1 ^{- [(} m 2 ^{- J} 2 ^{) V} 2 ^{+ Ц} 2 ^{] P}J 2 ⁺

—1             —1         —1—1

+ Ц2 Pj2+1} Pj1 -Pj3-...-Pjn + ... + ^^

^{+ {(} m N ^{- J}N ^{+ 1) V} N^PJN -1 ^{- [(} m N ^{- J}N ^{) V} N ^+Ц N ] ^PJN ⁺

+Ц NPJN+1} Pj1 PJ>jl'."' PJN-1 = 0.

Система линейных уравнений (5) будет иметь решение только в том случае, когда выражения в фигурных скобках равны нулю, так как P _hi ^ 0 . Следовательно, можно записать

^{( m} 1 ^{- j} 1 ^{+ 1)} Ц 1 ^Pj 1-1 ^{- [( m} 1 ^- Р "1 ) Ц 1 ⁺

^{+ V} 1 ] P 1 ^+V 1 P 1+1 = ⁰ ;

⁽ m 2 ^{- j} 2 ^{+ 1) Ц} 2 ^PJ 2-1 - ^[( m 2 - ^j 2 ^{) Ц} 2 ⁺

^{+ V} 2^{] P}J2 ^+V 2 P J 2+1 = ⁰ ,

⁽ m N - ^jN ^{+ 1) Ц} N^PJN -1 - ^[( m N -

^- J N ^{) Ц} N ^+V N ^{] P}JN ^+V N^PJN +1 = ^{0.          (}^⁾

Каждое уравнение системы (6) представляет собой систему уравнений СМО, состоящей из т . источников требований одного типа с одним обслуживающим прибором.

С целью решения полученной системы уравнений (6) для i -го типа процессоров перепишем ее следующим образом:

m i Ц i PP i =v i P > 1 i ,

[(m,. - k)Цi + Vi ]Pi = (m,. - k + 1)ЦiP-1 + ViPk+1, (7) v iPmi =ц iPmi-1, где Pi - вероятность нахождения системы в alk-м состоянии.

Введем   следующие   обозначения: при k ^ 1, zk = (mi - k)ЦiPk-1 +ViPk . Система уравнений (7) в этих обозначениях имеет следующий вид: zt = 0, zfc=zfc^1 = 0.

Таким образом, при всех k i 1, z _t = 0.

—1

P

mi ^!     p j. .рi

(         ■ Л I ^р i P 0 .

⁽ mi- ^- h i ^)!

Осуществляя обратную подстановку (8) в (3), с учетом биноминальных и полиномиальных коэффициентов [1]получим

N +1 -     N +1 _m I

P, , , =П P =П m i ^! р ^j-P_{0 0}       (9)

^j 1 , ^j 2 ,..., J n + 1 i =1 ^h i =1 ( m i - j . )!         ⁰,⁰,...,⁰ ,          ⁽v⁾

где P 0,₀,...,₀ - вероятность нахождения СМО в состоянии a ₀,₀,...,₀ , которая определяется по условию нормировки.

Структура графа исходной СМО показывает, что переход в состояние a _{h 1} , _h .. _{jN + 1} можно осуществить несколькими путями, причем вероятность нахождения в этом состоянии равна сумме вероятностей достижения его по каждому пути. Количество путей достижения состояния X_t , _j. в общем случае соответствует полиномиальному коэффициенту [2] и равно

!

X i , j .=         ^,

П j !

N                   i =1

где l = 0,1,..., ^ j.. Следовательно, i=1

P 0

X

j 2 =0, m 2

Р N+1 ml п    m1!   рj

N +1

П j i ! - =1 ⁽ m i ^- Ji ^)!

-1

.

Произведя подстановку (11) в (9), получим решение системы уравнений (2) в общем виде:

P j

,..., ^jN

l! N41    mi!

N+1    ПP

П j i ! ^- =1 ^{( m}- ^- Ji ^)!

i =1

X

j 2 =0, m 2

l!    N+1     mi!

N+1    ПP

П ji ! ^- =1 ⁽ mi ^- Ji ^)!

i =1

.

^jN =⁰, mN + 1

Основными показателями надежности МВС являются P ^Е - вероятность безотказной работы с заданной производительностью, k < - коэффициент готовности к работе с заданным уровнем производительности [3].

С учетом определенной вероятности P _{h 1} , _h 2 _{jN + 1} нахождения системы в состоянии a _{h 1} , _{h 2} ,..., _{jN + 1} показатели надежности микропроцессорных ЭВМ определяется следующим образом:

P ^Е= X

^j 1 , ^j 2 ,..., ^jN + 1 ’

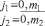
^j N+1 =⁰,m N + 1

K <

P^E =   P^E

P ^E- (1 - P ^E) = 2 P ^E- 1 ^.

Таким образом, в данной статье представлен аналитический метод расчета надежности функционирования многопроцессорных вычислительных систем, состоящих из произвольного количества типов процессоров, произвольного числа процессоров каждого типа и произвольного количества шин интерфейса, объединяющих процессоры с оперативной памятью.