Метод оценки отношения сигнал/шум на основе статистических характеристик выбросов случайных процессов применительно к командно-измерительной системе спутниковой связи

Какие бы функции ни выполнял космический аппарат (КА) на орбите, связь с

Землей ему необходима. Через эту связь он получает от Земли команды и задания, через неё же передает телеметрическую информацию. За этот радиообмен отвечает командноизмерительная система (КИС), состоящая из бортового (БС КИС) и наземного (НС КИС) сегментов.

Командно-измерительная система решает задачи приёма командно-программной информации с наземной станции, передачи телеметрической информации с космическим аппаратом на наземные станции и измерения текущих навигационных параметров.

Командно-измерительные системы имеют ряд особенностей, влияющих на построение систем спутниковой связи. Приведем основные из них [1].

• 1.    Командно-измерительные системы должны обеспечивать управление искусственными спутниками Земли в различных режимах его полета.

• 2.    Источники передаваемой по радиолиниям командно-измерительных систем информации находятся как на борту искусственного спутника Земли, так и на земле.

• 3.    Радиолинии командно-измерительных систем должны совмещать передачу информации с проведением измерений текущих навигационных параметров.

• 4.    Командно-измерительные системы должны обеспечивать повышенную достоверность передаваемой на искусственный спутник Земли информации с обязательным квитированием факта её прохождения.

Радиолиния командно-измерительной системы состоит из двух участков: Земля – космический аппарат и космический аппарат – Земля. Оба этих участка подвержены воздействию помех (например, атмосферные и космические помехи), в результате воздействия которых уменьшается мощность полезного сигнала и увеличивается мощность шума, что отрицательно сказывается на результирующем отношении сигнал/шум на входе приемного устройства командно-измерительной системы [2].

Если результирующее отношение сиг-нал/шум не будет обеспечено, то не будет выполняться энергетический запас командной радиолинии и приемное устройство командно-измерительной системы не сможет распознать входной сигнал. Следовательно, одной из важнейших задач в командно-измерительной системе и системах спутниковой связи в целом является оценка ее помехоустойчивости, потому что от этого напрямую зависит качество передачи информации. Помехоустойчивость системы необходимо оценивать исходя из определения отношения сигнал/шум.

Одним из возможных вариантов решения проблемы низкого отношения сигнал/шум является использование более совершенного оборудования. Так, например, можно применять передающие устройства с заведомо избыточной мощностью, антенны с большими зеркалами и в итоге добиться необходимого отношения сигнал/шум. Однако данный метод требует больших материальных затрат.

Другим вариантом решения данной проблемы является применение адаптивных систем. В основе работы таких систем лежит не-      5

посредственная оценка отношения сигнал/шум. Один из методов оценки отношения сигнал/ шум – последовательное измерение мощности шума и сигнала. Так, в момент, когда сигнал на входе приемного устройства командно-измерительной системы отсутствует, можно оценить мощность шума, а в момент приема сигнала измерить его мощность, соответственно, далее вычислить отношение полученных мощностей и определить искомое отношение сигнал/шум. Однако в данном случае потребуется большое количество времени для измерений, что не позволит вести оперативный контроль.

Наиболее перспективным методом оценки отношения сигнал/шум является метод оценки вероятностных характеристик выбросов случайных процессов, так как он основан на использовании статистического аппарата анализа, позволяющего получить высокоточные результаты измерений. Так, определяя среднее число положительных выбросов в единицу времени, можно найти отношение сигнал/шум.

Особенности данного метода рассмотрим на примере аддитивной смеси фазома-нипулированного сигнала и узкополосного нормального случайного процесса [3]:

х ( t ) = 5 ( t ) + ^( t ) = U m • П ⁽ t ) cos (^ t + Ф о ) ⁺

+ A(t) cos [ω0 t + θ(t)], где Um, шс - амплитуда и угловая частота сигнала 5(t); A(t) и 9(t) - огибающая и фаза случайного процесса ξ(t); φ0 – начальная фаза сигнала; П(t) - манипулирующая последовательность.

Для оценки отношения сигнал/шум в данном случае необходимо использовать информацию о числе выбросов аддитивной смеси х ( t ) (рис. 1), где под выбросом N понимается отрезок времени, в течение которого х ( t ) превышает заданный порог С .

■_■ ИССЛЕДОВАНИЯ

Havko-

ЖГРАДА

Достаточно полное вероятностное описание характера изменения выбросов может быть получено на основе известной инфор-

мации о совместной плотности распределения нормированной огибающей V и фазы θ

аддитивной смеси сигнала и узкополосного

где a = —m - отношение сигнал/шум; 1 0 - функция Бесселя.

Среднее число положительных выбросов в единицу времени можно найти, зная

случайного процесса и их производных

V ’ и

θ’ [4]:

^-Р 0

ш ( V , V ', 9 , 0' ) =

-V^г (2 п 2 ) о ² р"

exp <

2р 0

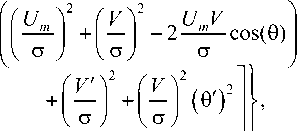
совместную плотность распределения, определяемую по (2), путем её интегрирования по производной огибающей V ’. Полученный результат можно представить в следующем в и де 4]:

м + (Г)~ ^-р 0 (of C )т- /^-р 0 C

N\ ( C ) = а П^ —® — T =а П^--

1 N 2п faj V 2п ст

exp

—a

f C V

IctJ

1 0 [ aac 1 ^T ' fCTJ

где р 0 - вторая производная от функции корреляции аддитивной смеси гармонического сигнала и узкополосного случайного процесса; σ – среднеквадратическое значение шума.

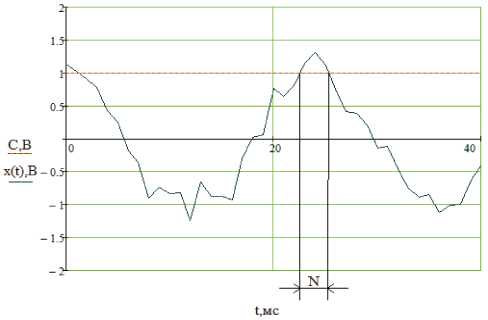
Рис. 1. Пересечение аддитивной смесью заданного уровня

Исходя из формулы (1) можно найти плотность распределения, позволяющую охарактеризовать огибающую аддитивной смеси статистически, исследуя характерные зависимости от различных параметров, которые можно использовать для определения отношения сигнал/шум. Для получения совместной плотности распределения огибающей и её производной следует выполнить двойное интегрирование многомерной плотности распределения ω( V , V ’, θ, θ’) по всем значениям фазы и её производной:

п п

ю ( V , V ' ) = _{J J ю} ( V , V ' , 9 , 0^ 0 d 0' =

-п -п

-V² о ^{3 -} 2 пр 0

где С – порог; T – время наблюдения.

Из (3) непосредственно следует, что характер зависимости от уровня С среднего числа выбросов огибающей узкополосного случайного процесса однозначно определяется исходя из изменения соответствующей плотности вероятности огибающей ω( С /σ) и сложившегося отношения сигнал/шум.

Само значение порога должно обеспечи- вать минимальную дисперсию числа пересе- чений, которая находится по формуле m2

” ^ + = mb I ( n c - N српр ) •

m

Nср.пер       A nc, m i=1

где m – число реализаций аддитивной смеси x ( t ); n _c – число пересечений каждой реализации с одним и тем же порогом; N _ср.пер – среднее статистическое число пересечений^. .

В табл. 1 приведены результаты вычисления дисперсии числа пересечений аддитивной смеси x ( t ) (исследования проводились для сигнала с амплитудой, равной 1 В), для a = 0, при трех значениях порога С (0, 0,5 и 1) и времени наблюдения T , равном 2000, 1000 и 500 мкс. Данные получены на основе результатов 10 реализаций для каждого времени наблюдения.

Как видно из табл. 1, минимальная дисперсия числа пересечений достигается во всех случаях при значении порога С, равном 1 В. Также необходимо отметить, что, проводя исследования для сигналов с амплитудой от 2 до 10 В (результаты исследований не приво- дятся), было установлено, что минимальная дисперсия числа пересечений достигается при пороге, равном амплитуде исследуемого сигнала.

Таблица 1

Результаты вычисления дисперсии числа пересечений

C	T = 2000 мкс		C	T = 1000 мкс		C	T = 500 мкс
	N 1 +	_ 2 σ N 1 +		N 1 +	2 σ N 1 +		N 1 +	2 σ N 1 +
0 В	24,5	6,84	0 В	12,4	3,21	0 В	6,36	1,31
0,5 В	13,8	4,86	0,5 В	7	2,9	0,5 В	3,64	1,71
1 В	0,28	0,281	1 В	0,12	0,16	1 В	0,08	0,074

На рис. 2 приведен график поверхности среднего числа положительных выбросов аддитивной смеси (для сигнала с амплитудой 1 В) в зависимости от отношения сигнал/шум и порога С , установленного на единичной отметке, времени наблюдения, равно м 1 с, и р 0 , в данном случае равным π /6 ∆ f _э [4], где Δ f _э – ширина энергетического спектра шума в рассматриваемой системе.

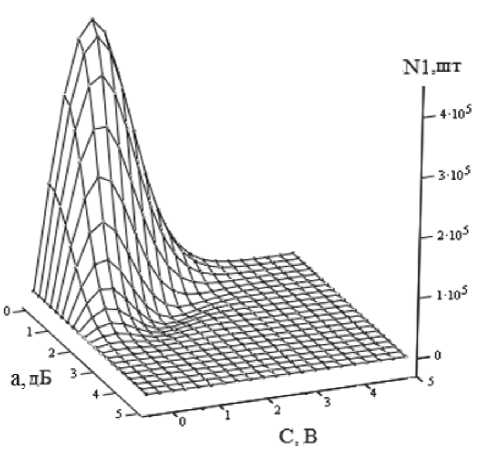
Рис. 2. График поверхности зависимости среднего числа положительных выбросов от отношения сигнал/шум и порога С при Δ f _э = 1 МГц

На рис. 2 видно, что при отношении сигнал/шум, равном нулю (то есть при отсутствии сигнала), среднее количество выбросов принимает максимальное значение. При увеличении отношения сигнал/шум среднее количество выбросов уменьшается и достигает минимальной величины при a ≈ 3 дБ.

Из проведенного анализа следует, что, зная среднее количество выбросов, можно выполнить оценку отношения сигнал/шум аппаратным путем. Так, на основе анализа статистических характеристик выбросов случайных процессов разработано устройство измерения отношения сигнал/шум, упрощённая структурная схема которого приведена на рис. 3.

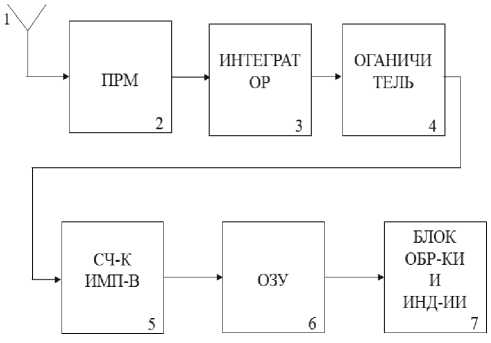
Рис. 3. Вариант реализации устройства оценки отношения сигнал/шум по статистическим характеристикам выбросов случайных процессов

В соответствии со структурной схемой в приёмнике командно-измерительной системы 2 формируется аддитивная смесь полезного сигнала и шума, которая далее поступает на интегратор 3, в котором определяется целое значение порога С , по формуле

n

Е И

С = ^— ,

n

L          -I ц где n - общее число отсчетов аддитивной смеси; Ui – значение каждого i-го отсчета.

Далее на ограничителе 4 выставляется порог в соответствии со значением, полученным в интеграторе. Ограниченная порогом аддитивная смесь преобразуется в прямоугольные импульсы, поступающие на счетчик импульсов 5. Результат представляет собой число, записывающееся в ячейку памяти (оперативное запоминающее устройство) 6, в которой по формуле (3) определяется искомое отношение сигнал/шум. Полученный результат далее поступает в блок обработки и индикации 7, в котором отношение сигнал/шум

■_■ ИССЛЕДОВАНИЯ

Havko-

ЖГРАДА

конкретизируется в соответствии с заданной зависимостью. Найденное значение отношения сигнал/шум выводится на встроенный в данном блоке индикатор.

Разработанный метод в конечном счете позволит вести оперативный контроль над измеряемыми параметрами сигналов. По результатам данной оценки можно принять меры, направленные на повышение помехоустойчивости командно-измерительной системы. К таким мерам относятся:

• 1)    управление мощностью передающего устройства;

• 2)    помехоустойчивая обработка сигналов (например, вейвлет-обработка);

• 3)    регулирование и управление диаграммами направленности используемых антенн;

• 4)    применение помехоустойчивого кодирования.